基于LLE非线性特征的ANFIS施工振动风险评估

郭 亮，周 晶

(大连理工大学 建设工程学部， 辽宁 大连 116023)

施工振动环境影响的相关理论研究，对施工振动风险的传播过程进行风险识别。一方面由振源引起的振动经土壤传播，可能导致场地土壤的致密化进而引起场地周围建筑物的基础沉降，另一方面，场地土壤与建筑物基础的相互作用使建筑结构产生振动响应，进而可能造成建筑物的损坏或对建筑物中的居住者和精密仪器的产生干扰。根据不同的风险目标，把施工振动风险分为建筑物沉降风险、建筑物振动风险和居住者风险三部分[1]。

风险可以表示为R(风险)=P(概率)×C(后果)，即损失发生的可能性。根据风险的定义，将施 工振动环境风险定义为施工振动对周围环境造成影响或损坏发生的可能性[2-3]。其中，精密仪器仪表被作为具有特殊属性的居住者考虑而被划分到居住者风险中。针对系统中的风险对象(建筑物和居住者)，并参考文献中的滑坡风险模型[4]，如公式(1)所示。

R(PD)=P(H)×P(S)×V(P)×E

(1)

其中，R(PD)是指滑坡风险；P(H)是指滑坡事件发生的可能性；V(P)是指对象的损坏发生的可能性；E是指对象的价值。其中，Hao H等[5]认为P(S)×V(P)×E可以被看作风险结果。Mohammad[6]认为P(H)×P(S)可以被看作风险发生的危险性。参照公式(1)提出了施工振动风险模型，如公式(2)所示：

R(v)=H(v)×V(v)×C(v)

(2)

其中：R(v)是施工振动风险；H(v)是指施工振动对于风险对象的危险发生的可能性，简称危险性；V(v)是指风险对象损坏的可能性，简称易损性；C(v)是指风险后果的严重性或可能的风险损失，其中H(v)×V(v)也可以被看做是风险发生的可能性[7-8]。专家系统的知识框架也是基于施工振动环境风险模型建立的。

施工振动风险评估知识体系由专家在进行风险评估时考虑的影响因素组成，并在文献收集和专家调查的基础上建立起来的[9-10]。根据对施工振动环境风险的传播过程，将施工振动风险分为建筑物风险和居住者风险两部分，其中建筑物风险又分为建筑物沉降风险和建筑物振动风险[11]。根据施工振动环境风险模型，将危险性模块、易损性模块和重要性模块集成为风险，施工振动风险评估指标体系的知识框架如图1所示：

图1施工振动风险评估模型指标体系

1 LLE非线性特征提取方法

根据专家系统提取多个样本的施工振动风险特征可以得到一组特征向量集，该特征向量集中含有一些对与施工振动无关的冗余特征信息，并且特征集本身都是线性的组合堆砌，如何获得能够反映施工振动特征的非线性特征，是一个亟待解决的问题[12]。本文在此基础之上，采用了局部线嵌入算法(Locally Linear Embedding,LLE)对获得的线性特征数据集进行二次特征提取得到非线性特征。下面将首先对局部线性特征嵌入算法进行介绍以便后续的应用。

局部线性嵌入算法在数据整体非线性的前提下假定局部意义下的数据结构是线性的，它是一种依靠局部线性来逼近整体非线性的流形算法。算法在保持局部几何特性不变的条件下，将局部邻域相互重叠以提供高维数据降维后的整体特性信息[13]。

LLE算法的实质就是把高维特征数据集合A={a1，a2，…，an}，ai∈RD映射到低维特征数据集合B={b1，b2，…，bn}，bi∈Rd(D>d) 。其算法步骤主要分为3步：

(1) 计算高维特征数据空间中每个样本点ai(i=1,2,…,n)与其他n-1个样本点之间的距离，依据样本点相互之间距离的大小，选取前K个和ai(i=1,2,…,n)距离最近的点作为其邻域。其中两点之间距离的度量标准采用欧式距离，即dij=‖ai-aj‖；

(3)

(4)

2 自适应模糊神经网络推理系统(ANFIS)

自适应模糊神经网络推理系统(Adaptive Neuro-Fuzzy Inference System abbr, ANFIS)是华人学者Jyh-Skiing Roger Jang在1993年提出的一种神经网络与模糊理论相互结合的集成系统，该系统利用神经网络的拓扑结构表达模糊推理系统，通过其中的各个神经元实现各种模糊运算，采用神经网络理论中误差反向传播和最小二乘估计相结合的混合算法自适应地调整系统参数，逼近输入输出数据之间的隐含关系[14-15]。该模糊神经网络系统具有模糊推理功能和映射逼近能力，已在系统辨识等多个领域中得到了尝试和应用。

2.1 ANFIS的系统结构

ANFIS是多输入单输出系统，不失一般性，以Sugeno型模糊系统为例对其进行阐述。设系统具有两个输入x，y和一个输出f对于一阶Sugeno，典型的模糊if-then规则表达为：

ifxisA1andyisB1thenf1=p1x+q1y+r1

(5)

ifxisA2andyisB2thenf2=p2x+q2y+r2

(6)

相应的ANFIS结构如图2所示。图2中，节点之间的连线只表示信号的传递方向，没有权值与之关联。方形节点表示其中的参数可以调整，圆形节点表示其中的参数固定。各层节点的功能如下：

第1层：每个节点与一个系统输入连接，对输入变量进行模糊化处理，输出对于节点相应模糊集的隶属度

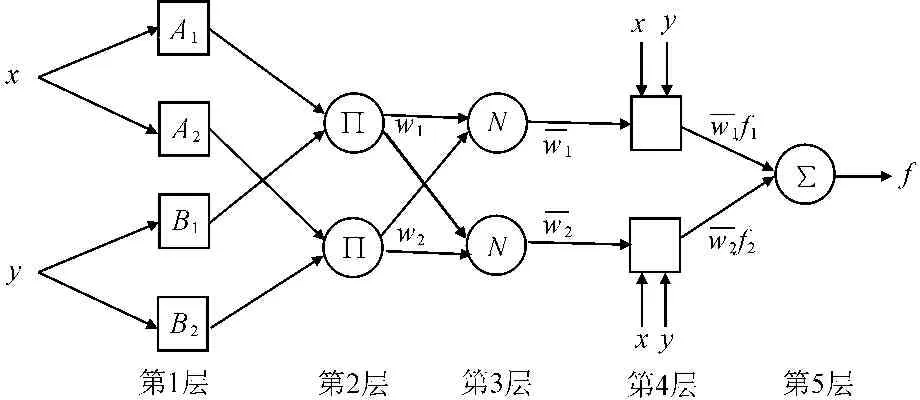
图2 ANFIS结构

O1i=uAi(x)，i=1，2；

(7)

O1i=uBi-2(y)，i=3，4；

(8)

根据节点对应的隶属度函数，可以得到相应的条件参数集合。对于广义钟形隶属度函数

(9)

条件参数集为所有参数{ai，bi，ci}组成的集合。

第2层：每个节点表示一条产生式规则，与第1层中表示相应规则条件的节点连接，对输入进行模糊乘积运算，输出每条规则的适用度

O2i=wi=uAi(x)×uBi(y)

(10)

第3层：每个节点对应一条规则，与第2层中的所有节点连接，对各条规则的适用度进行归一化处理

(11)

第4层：每个节点与第3层中的对应节点以及系统的全部输入连接，计算相应规则的输出

(12)

结论参数集为所有参数{pi，qi，ri}组成的集合。

第5层：只有一个节点，与第4层中的所有节点连接，计算所有规则的输出之和

(13)

2.2 ANFIS学习算法

ANFIS采用误差反向传播与最小二乘估计相结合的混合算法对系统可变参数进行调整。对于参数可调整的自适应网络而言，其中的线性参数可以采用最小二乘方法来辨识，而非线性参数可以采用误差反向传播算法来辨识。由ANFIS的网络结构可见，当条件参数固定时，系统的输出可以表示为结论参数的线性组合，即

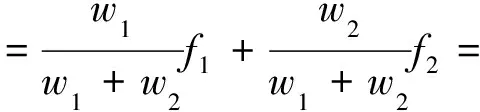
(14)

因此，可以采用误差反向传播与最小二乘估计相结合的混合算法调整ANFIS的参数。在每次迭代计算过程中，当系统输入正向传递时，固定条件参数，采用最小二乘估计方法调整结论参数;当输出误差反向传播时，固定结论参数，采用梯度下降法调整条件参数。对于己知的条件参数，通过这种方式可以得到全局最优的结论参数，这样不仅可以降低梯度下降法中搜索空间的维数，而且可以显著提高收敛速度[14]。

3 LLE非线性特征与ANFIS相结合的方法

LLE方法提取了表征振动施工风险特征指标体系多维特征向量的低维非线性特征，将表征高维特征指标体系的特征向量降维得到更低维数的振动施工风险非线性特征向量。以此为ANFIS学习方法的向量输入对不同场地的施工振动风险进行评估。该方法的具体实现步骤如下：

(1) 以一系列实际施工工程为研究对象，按照图2所示的指标体系提取表征施工振动风险的具体指标，得到一组表征施工振动风险的高维特征向量。

(2) 分别将每个高维特征向量中的每个分量进行归一化处理，组成一个归一化的表征该工程施工振动风险的高维特征向量。

(4) 利用已知施工振动风险等级的工程样本的低维非线性特征作为训练样本训练ANFIS神经网络，然后将验证样本的低维非线性特征向量值输入到ANFIS神经网络中获取样本的施工振动风险评级分类结果。

4 实际工程应用

为了验证提出方法的有效性，将基于LLE非线性特征的ANFIS方法应用于实际工程，对该工程的施工振动风险进行评估。

英国杜伦大学校图书馆扩建和新建Gateway办公楼工程(简称Gateway项目)规划所在地由于曾用于煤矿开采。所以，在场地内埋置有若干未拆除的混凝土竖井，在混凝土竖井和原有地上构筑物的拆除过程中产生了巨大振动，对周围环境产生了巨大影响。在工程开工建设前期的项目风险评估阶段，需要对工程施工过程中产生的施工振动所带来的风险进行评估。项目规划所在地两面紧邻道路，另一面距离原有工程办公楼仅有6 m左右距离。所以，建筑物施工过程中产生的巨大振动响应会对已有建筑物结构安全产生一定威胁，并对工作在已有建筑物中的工作人员的工作生活产生了干扰。鉴于此，把工程办公楼施工振动作为风险目标，拟采用基于LLE非线性特征的ANFIS方法对施工振动风险进行评估,在分析的过程采用Matlab软件平台相关工具包进行计算分析。

按前节中步骤(1)所述，依据图1所示的指标体系提取ANFIS神经网络训练样本施工振动风险的具体指标特征，随机多次提取可得到不同样本的一组表征施工振动风险的高维特征向量，为了计算方便需要将高维特征向量进行标准化处理，标准化处理后的结果如表1所示。

其中类别1，2，3，4分别表示类别为轻微或无振动风险，一般振动风险，严重振动风险，非常严重振动风险的训练样本。

表1 训练ANFIS神经网络的样本

按照步骤(4)使用提取到的训练样本的低维特征向量对ANFIS神经网络进行训练。然后将实际工程检验样本振动风险指标向量经LLE特征提取后输入到训练好的ANFIS神经网络中进行风险评估识别。对待检验的实际工程振动风险样本的指标特征向量进行LLE非线性特征提取后利用ANFIS神经网络进行风险评估识别(方法1)，评估结果如表2所示。振动施工风险检验样本的高维特征不经过LLE特征提取直接输入到ANFIS中进行风险评估识别(方法2)结果如表3所示。

表2 方法1样本经ANFIS评估识别的输出结果

表3 方法2样本经ANFIS评估识别的输出结果

由以上分析结果可见方法1除了错分两组样本之外其余样本全部分类正确，而方法2则错分8组。可见基于LLE非线性特征提取的ANFIS方法同方法2相比提高了施工振动风险识别的精确度。且由表1可以看出本文实际项目的施工振动风险等级为轻微风险，施工时对周围建筑物的影响较小，可以进行实际施工。

5 结 论

提出了一种基于LLE非线性特征的ANFIS施工振动风险评估方法。该方法融合了更大的信息量，不仅使原振动风险指标中包含的信息通过非线性低维特征分量得以充分体现，而且还简化了系统间特征信息的干涉或耦合。最后通过ANFIS神经网络识别分类，将本文方法与传统振动风险特征参数特征提取识别方法进行比较，识别结果证明了本文方法提高了特征提取和振动风险评估的精度，可以作为一种振动风险评估方法应用于实际工程振动风险评估中。