红外光谱在铁基超导材料研究中的应用

2018-08-21戴耀民

物理学进展 2018年4期

戴耀民

超导物理与材料研究中心，固体微结构国家实验室，南京大学物理学院，南京210093

I.引言

雨后的七色彩虹是光被雨滴折射产生；中国古代以铜为镜，因为磨光的金属可以很好的反射光线；我们可以透过窗户看到外面的世界，是由于玻璃可以透光。我们生活中这些司空见惯的现象都源于光与物质的相互作用。可以说我们用眼睛看任何事物的时候，都是在借助光与物质的相互作用来认识世界。然而，光是一种具有很宽波长范围的电磁波，从无线电波到红外、可见、紫外、X射线，甚至到γ射线，其中只有很窄的波长范围（可见光）可以被人眼看到，大大限制了我们通过光来认知事物的能力。光谱学的产生和发展突破了人眼的局限，为我们开启了新的“视界”。

固体材料中集体激发模式的特征能量大多分布在meV到几个eV的能量范围，如图1所示。例如：金属材料中的载流子散射速率一般为几个到几十meV；超导材料的超导能隙通常为几个到十几meV；电荷密度波或自旋密度波能隙对应的能量尺度一般是几十到几百meV；半导体材料中的带隙宽度大约是几个eV等。这些集体激发的特征能量恰好处在光谱学研究的能量范围，因此，光谱，特别是红外光谱发展成一门凝聚态物理研究中非常重要的谱学手段。由于一些历史原因，在红外光谱学中我们通常用波数作为能量的量度，这里的波数定义为波长的倒数1/λ，其中λ表示波长。我们用cm−1作为波数的单位，cm−1与其它常用能量单位的换算关系如下：

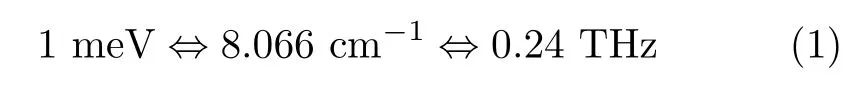
光谱手段探测的能量范围通常是从大约10到55000 cm−1，相当于1.25 meV到6.9 eV。固体材料的光学性质和光子能量的依赖关系可以用多种实验方法测量。例如：光栅分光法，椭偏光度法，傅立叶变换光谱，时间分辨THz光谱等。

图1.固体材料中各种集体激发模式的特征能量分布。

本文系统地介绍傅立叶变换光谱仪的基本原理和实验技术，以及红外光谱在铁基超导材料研究中的应用。文章分为5个部分，从第II节到第VI节。第II节简单介绍傅立叶变换光谱仪的基本工作原理；第III节介绍测量固体样品的绝对反射率使用的原位镀膜技术；在第IV节里，我们介绍数据处理以及数据分析中常用到的方法和理论模型；第V节基于铁基超导体发现以来发表的相关文章，综合讨论红外光谱在铁基超导材料研究中的应用；最后，第VI节对本文进行总结。

II.傅立叶变换光谱仪的基本原理

图2.迈克尔逊干涉仪的光路示意图。

傅立叶变换光谱仪核心部分是一个迈克尔逊干涉仪。为了方便理解傅立叶变换光谱仪的基本原理，我们从一个简单的迈克尔逊干涉仪开始。图2展示的是迈克尔逊干涉仪的光路示意图。从光源(Source)发出的光被分束镜(BMS)分成强度相等的两束。其中一束透过分束镜进入装有定镜(Fixed Mirror)的一臂，另一束被分束镜反射进入装有动镜(Moving Mirror)的一臂。两束光分别被定镜和动镜反射后，再次在分束镜处汇合并发生干涉，干涉后的光进入探测器(Detector)。

图3.(a)利用傅立叶变换光谱仪测得的远红外区光强随动镜位置的变化曲线I(x)；(b)光强和频率的依赖关系曲线I(ν)，由面板(a)中的曲线进行傅立叶变换得到。

为了使问题简单，我们首先考虑一束波长为λ的单色光（例如：激光）进入迈克尔逊干涉仪。如果连续改变动镜的位置，迈克尔逊干涉仪两臂的光程差会连续发生变化。当干涉仪两臂的光程差是半波长λ/2的偶数倍时，两束光干涉相涨，探测器处接收到的光强信号最强；当两臂的光程差是λ/2的奇数倍时，两束光干涉相消，探测器接收到的信号最弱。于是，我们可以得到光强随动镜位置连续变化的一条谱线，记作I(x)，将I(x)进行傅立叶变换，即可以得到光强关于频率的谱线I(ν)（也称为功率谱）。例如，激光的I(x)谱是正弦或余弦函数，其傅立叶变换I(ν)是δ函数，和单色光的特点完全相符。如果进入迈克尔逊干涉仪的是含有各种波长的复色光，原理和方法完全相同。由于测量过程中需要进行一次傅立叶变换，因此这种光谱测量方法称为傅立叶变换光谱。图3(a)是利用傅立叶变换光谱仪得到的远红外区I(x)谱，图3(b)是傅立叶变换得到的相应的I(ν)谱。傅立叶变换光谱仪的优势在于它的动镜扫描一次即可同时采集不同频率的信息，大大提高了光谱数据采集的效率。

图4显示了Bruker公司生产的IFS 66 v/s型傅立叶变换光谱仪的光路示意图。光谱仪配备的每个光源都有各自的特征功率谱，不同的分束器有各自的特征透过率曲线，并且不同的探测器也表现出完全不同的频率响应，表格I给出了不同光源、分束器和探测器的使用范围。因此，傅立叶变换光谱仪测量的光谱范围由光源、分束器以及探测器的组合得到的最窄频率范围决定。例如，Globar光源、Silicon 3 mm分束器和4.2 K Bolometer的组合可以测量的光谱范围是50∼600 cm−1。

图4.Bruker IFS 66 v/s型傅立叶变换光谱仪的光路示意图。

表I.常用的光源、分束器和探测器工作的光谱范围。

III.原位镀膜技术测量反射谱

要测量材料的绝对反射率，我们需要一个反射率已知的材料作为参比。通常情况下，金、银或铝等反射率比较高的金属被用做参比。通过测量材料相对于参比的反射率谱，我们可以计算得到材料的绝对反射率。要使绝对反射率的测量比较精确，还需要待测样品大于光斑尺寸，且参比和材料具有相同表面形貌，以及两者反射后的光路重合等苛刻条件。然而，最新发现的材料和科学界最感兴趣的材料往往都非常小，而且形状也非常不规则，给绝对反射率的准确测量带来了极大困难。

原位镀膜技术的发明解决了小而不规则的样品绝对反射率测量的难题[33]。该技术在样品表面原位蒸镀一层金膜（高频区域用银或铝），并用这层金膜作为样品自身的参比来测量其反射率。这种测量方法一方面使样品的整个表面得到了利用，提高了测量的信噪比；另一方面，使参比和样品具有完全相同的形状和表面形貌，几乎完全消除了由样品和参比的几何差异引起的几何效应。

图5.原位镀膜装置的结构示意图。

图5展示了原位镀膜装置的结构示意图。由于镀膜过程必须在高真空环境下完成，整个系统都安装在一个真空罩中（数字6所示）。真空罩的中心处是恒温器的冷头（数字5所示），方形冷头互相垂直的两个侧面装有两个铜锥，铜锥顶部用来粘样品和不锈钢反射镜。照到铜锥上的光会被反射至其它方向而不进入探测器。防辐射罩（数字4所示）将外部环境的热辐射反射回去，确保冷头温度可以降至液氦温度(4.2 K)。冷头部分以及防辐射罩可以在真空下旋转90度。数字1所示部分是一段绕着金线的钨丝。当给钨丝通电流时，可以看到钨丝被点亮，金线被熔化。逐渐增加电流，直至金被蒸发出去，从而在样品的表面生成一层金膜。这层金膜便可作为样品自身的参比来测量样品的绝对反射率。

利用原位镀膜技术测量样品绝对反射率的详细过程如下：(1)测量不锈钢反射镜的功率谱，得到IMirror；(2)转动样品杆90度角，使样品正对入射光，测量样品的功率谱ISam，并除以IMirror，得到ISam/IMirror；(3)在样品表面镀金；(4)再次测量不锈钢反射镜的功率谱；(5)转动样品杆，测量有金膜覆盖的样品的功

率谱ICoatedSam，并除以IMirror，得ICoatedSam/IMirror。最后，由下式计算样品的绝对反射率

这里用一个不锈钢反射镜作为中间参比是为了消除升降温过程中由于系统漂移引起的误差。利用原位镀膜技术测得的反射率具有非常高的精度，其绝对误差小于0.5%，相对误差小于0.1%。

图6.利用原位镀膜技术测得的Ba0.6K0.4Fe2As2远红外波段的绝对反射率。

图6中红色平滑曲线表示用原位镀膜技术测得的最佳掺杂Ba0.6K0.4Fe2As2单晶样品远红外波段的绝对反射率RSam；粉色和蓝色曲线分别表示ISam/IMirror和ICoatedSam/IMirror谱线。由于样品尺寸小于光斑和不锈钢反射镜，形状不规则，且解理后的表面有台阶，这些因素导致ISam/IMirror谱线整体低于样品实际的反射率，并且出现几何效应引起的各种微小结构。注意这些微小结构在绝对反射率曲线RSam上都被消除。

IV.光电导以及常用的理论模型

A.光电导和Kramers-Kronig关系

在凝聚态物理的研究中，光电导的实部 σ1(ω)可以方便而直接地反映材料中各种集体激发的信息。由Kubo-Greenwood公式

可知，σ1(ω)和材料中的联合态密度Ds′,s(ω)有直接关系（ps′,s表示s和s′态之间电偶极子跃迁矩阵元），因此可以用来获得固体材料中电子态密度的信息。例如，超导材料中超导能隙的打开导致费米面附近的电子态密度丢失[14,47]，电子凝聚成Cooper对；电荷或自旋密度波能隙、赝能隙引起低能电子态密度降低而高能部分电子态密度增加[11,13,36,37]；这些现象都可以从光电导谱上直接观测到。另外，光电导是一个线性响应函数，材料的总光电导是不同集体激发对应的光电导的简单线性叠加，因此我们可以从光电导谱上区分出不同的集体激发模式。比如，晶格振动的集体激发在光电导谱上对应于一个尖锐的吸收峰[32,87]；电子的带内跃迁在光电导谱上形成一个以零频为中心的峰，称为Drude峰[11,14,47]。

利用傅立叶变换光谱仪和原位镀膜的方法，我们可以精确测量固体材料的绝对反射率，因此需要由测得的绝对反射率计算光电导谱。我们知道，材料的光学常数都是复响应函数，包括实部（幅度）和虚部（相位）。例如，被界面反射的电磁波需要用幅度(R)和相位(ϕr)描述，实验测量的材料绝对反射率就是复反射率函数的幅度。Kramers和Kronig研究了这些光学常数的实部和虚部之间的关系，发现这些光学常数的实部和虚部并不是独立的。利用因果律可以得到光学响应函数的实部和虚部之间一系列重要关系，这些关系被称为Kramers-Kronig关系，简称KK关系。只要在很宽的频率范围内测得材料的绝对反射率R(ω)，其相应的相位信息ϕr(ω)就可以用KK关系得到，再经过一些简单的公式运算，所有的光学常数都可以获得。傅立叶变换光谱中最常用的R(ω)和 ϕr(ω)的KK关系表达如下

其中P表示柯西主值。这个公式表明，要计算ϕr(ω)，我们需要从零频到无穷范围内测量R(ω)，这在实验上是不可能做到的。为了使用KK关系，我们通常在尽量宽的频率范围内测量材料的反射率，从THz(10 cm−1)到紫外区域(55000 cm−1)，再利用合适的外推公式将数据外推至零频和无穷。表II给出了常用的低频和高频极限的外推公式。

表II.KK分析中常用的低频和高频极限的外推公式。

在KK分析中，选择合理的外推公式是非常重要的。例如，好的金属在红外和THz区域具有很高的反射率，并且随着频率的降低很快趋近于1。因此，金属的低频端通常用Hagen-Rubens公式来外推。对于绝缘体，我们通常用一个常数作为低频极限的外推公式。在高频端，我们一般用带间跃迁(interband transition)接自由电子(free electron)频率响应作为外推公式，因为在足够高的频率区域，材料中的所有电子都可以被看做自由电子。有了实验上在很宽频率范围测得的反射率，再加上合理的低频和高频极限外推公式，我们可以利用公式(4)中的KK关系计算出相位的色散关系，然后可以利用表IV.A给出的各光学常数之间的关系式得到所有其他光学常数，包括光电导的实部σ1(ω)。

B.Drude和Lorentz色散理论模型

为了定量描述材料的光谱学性质，并从中提取出更多的物理，我们通常需要借助于一些简单的理论模型。这里介绍光谱研究中最常用的Drude色散理论模型和Lorentz色散理论模型。

Drude色散理论模型用来描述材料中自由载流子或带内跃迁的光学响应。在这个理论模型中，我们关心的光电导实部的频率响应由以下方程描述其中n表示自由载流子浓度；m表示电子质量；1/τ表示自由载流子的散射率；Ωp表示等离子体频率，定义为表示真空阻抗；σdc表示直流电导率。从公式(5)可以看出，Drude模型σ1(ω)的频率响应只用两个参量就可以确定，一个是等离子体频率 Ωp（或载流子浓度n），一个是散射率1/τ。图7(a)展示了Drude模型 σ1(ω)的频率响应曲线，其中使用的参数为 Ωp=5000 cm−1和1/τ=100 cm−1。

在零频极限下ω=0，方程(5)变为

这便是直流电导率的表达式。因此，光电导在零频的值恒等于直流电导率。令σ1(ω)=σdc/2，可得ω=1/τ。表明Drude理论色散曲线的半高宽便是系统自由载流子的散射率1/τ。对 σ1(ω)积分得

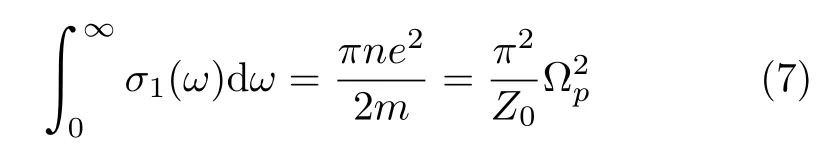
由上式可见，Drude模型中 σ1(ω)谱线下的面积正比于载流子浓度，且只由载流子浓度决定。

图7.(a)由Drude色散理论模型计算得到的光电导谱，计算中所取的参数为 Ωp=5000 cm−1和1/τ=100 cm−1。(b)由Lorentz色散理论模型计算得到的光电导谱，其中使用的参数为 ω0=1000 cm−1，γ=100 cm−1，以及S=2000 cm−1。

Lorentz色散理论模型用来描述材料中束缚电荷或带间跃迁的光学响应，比如晶格振动（声子），绝缘体中的电荷（带间跃迁）等。Lorentz模型中光电导实部的频率响应表示为

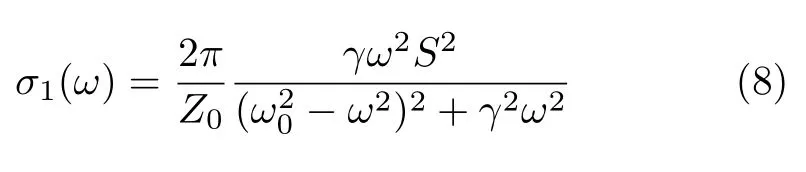
其中，ω0表示共振频率；γ表示共振线宽；S表示共振强度。图7(b)给出了Lorentz色散理论模型中σ1(ω)的频率响应曲线，其中使用的参数为 ω0=1000 cm−1，γ=100 cm−1，且S=2000 cm−1。Lorentz模型的σ1(ω)的频率响应曲线是一个以共振频率ω0为中心的尖峰，峰的半高宽即共振线宽γ，光电导峰下的面积正比于共振强度S，比如带间跃迁强度或声子数等。

V.红外光谱在铁基超导材料研究中的应用

超导现象自从1911年被荷兰物理学家Kamerlingh Onnes发现以来始终以其独特的魅力深深地吸引着世界各国的物理学家。一方面由于超导材料在军事、医疗、能源等领域有着广阔的应用前景，另一方面由于超导是量子现象的宏观表现，其中蕴藏着丰富而有趣的物理，一直激发着物理学家的好奇心。1957年，美国的三位物理学家Bardeen,Cooper和Schrief f er揭示了超导现象背后的物理机制：电–声相互作用使得费米面附近动量相反的两个电子配对（Cooper对），从而形成超导凝聚[3,4]。这便是著名的BCS理论。Bardeen,Cooper和Schrief f er因BCS理论的提出，被授予1972年的诺贝尔物理学奖。超导电性的BCS理论仅适用于描述早期发现的汞、铅等超导材料的超导机制，这类超导体被称为常规超导体。

超导领域发展的一个世纪以来，人们已经发现几千种超导材料，不仅包括汞，铅等常规超导体，还包括铜氧化物高温超导体，重费米子超导体等。后者的超导电性物理机制无法用基于电–声耦合的BCS理论描述，被称为非常规超导体。2006年，日本的Hosono科研小组报导了LaFePO中存在超导电性[41]，由于该材料中含有铁元素，因此被称为铁基超导体。第二年，一个类似的超导材料LaNiPO被同一个科研小组发现[84]。但是由于这些材料的超导临界温度(Tc)都非常低（低于5 K），他们的发现并没有引起物理学家的广泛关注。2008年，他们在掺氟的砷化物LaFeAsO1−xFx中发现超导电性，并且超导临界温度达到了26 K[42]，高压下可达到43 K[78]，从此铁基超导体研究的热潮拉开了帷幕。一方面需要探索新的，临界温度更高的铁基超导材料，另一方面需要理解这类材料中引起超导电性的机制。很快，中国科学院物理研究所赵忠贤领导的科研小组利用Sm元素去替换LaFeAsO1−xFx中的La元素，将超导临界温度提升到了55 K[62]。这些化合物具有ZrCuSiAs-型层状结构，被归类为1111体系。仅在一年的时间里，铁基超导体迅速扩展到六个体系。包括以掺杂的BaFe2As2为代表的122体系[65,71]，以LiFeAs[79,83]和NaFeAs[60]为代表的111体系，以FeSe[35]和Fe(Se1−xTex)0.82[23]为代表的11体系，以及结构更为复杂的层状结构化合物(Sr3Sc2O5)Fe2As2[94]和(Sr4V2O6)Fe2As2[93]则代表着32522和21311体系。后来，更多的铁基超导材料体系被发现，例如以Ca1−xLaxFeAs2为代表的112体系[44]，以CaAFe4As4(A=K,Rb,Cs)和SrAFe4As4(A=Rb,Cs)为代表的1144体系[39]等。另外，制备薄膜是与探索新材料或新体系并行发展的提高超导临界温度的途径。2012年，清华大学薛其坤领导的科研小组神奇地发现，将单晶中超导临界温度只有9.4 K的FeSe在SrTiO3衬底上做成只有一个原子层厚度的薄膜，利用扫描隧道显微镜观测到的超导能隙竟然达到了20.1 meV，比单晶样品的超导能隙(2.2 meV)大了将近一个量级。并且，超导能隙一直到42.9 K仍然能清楚地被观测到[82]。随后，上海交通大学的贾金锋科研小组利用原位四电极的方法测量了单层FeSe薄膜的电阻曲线，他们发现该样品的超导临界温度高达109 K[25]。几乎同时，中国科学技术大学的陈仙辉科研小组通过在FeSe层中间插入(Li/Fe)OH层，获得了(Li0.8Fe0.2)OHFeSe，其超导临界温度达到40 K[50]。

表III.常用的光学常数之间的关系表达式。

铁基超导体表现出许多非常规的特性。比如，这类超导体的母体通常是泡利顺磁性的坏金属，在低温下发生结构相变和自旋密度波(SDW)相变，进入反铁磁相[10,19,66]。对母体进行电子或空穴掺杂都会压制反铁磁相，当反铁磁相被压制到一定程度，便在FeAs面内出现超导电性。在温度–掺杂(T−x)相图中，超导相对应的区域呈一个拱形区域，最佳超导临界温度通常出现在反铁磁序的边界，即反铁磁相变温度被压制到零的区域附近[53]。最佳掺杂样品正常态的电阻通常表现出非费米液体行为[27,43,73]。一方面理论计算表明铁基超导体中的电子–声子耦合（电–声耦合）无法导致如此高的超导临界温度[6]，因此，超导电性极有可能是由于强关联效应或反铁磁自旋涨落[54]所导致。然而，另一方面这类超导材料中发现了很强的同位素效应[48]，说明电–声耦合对超导电性的出现起到一定的作用。于是，有关铁基超导体中超导电性机理的许多有趣问题摆在了物理学家的面前：这类超导材料的序参量的对称性是那种？s波对称，d波对称，还是理论预言的s±[54]？该体系中是否如铜氧化物一样存在赝能隙？磁性和超导电性的关系是什么？相互竞争还是共同起源，相互依存？引起电子配对的机制是什么？电–声耦合？自旋涨落？还是两者都有贡献或是其它？最佳掺杂样品正常态普遍存在的非费米液体行为是什么起源？和超导电性是什么关系？在这一节中，我们以近几年发表的文章为基础[12−15,87]，详细讨论如何利用红外光谱对以上问题进行研究。

A.超导能隙，配对对称性

每当一类新的超导材料被发现，物理学家首先关心的是超导能隙的大小以及对称性，因为这些信息直接关系到超导电子配对的机制。理论计算表明铁基超导体是一类非常规超导体。这类材料中有多个Fe的3d轨道形成的能带穿过费米能级，形成了多个费米面。布里渊区中心Γ点附近是空穴型的费米面，而布里渊区边界M点附近是电子型费米面[75−76,89]。其电子配对态是由反铁磁自旋涨落引起的，由此导致的超导能隙具有s±对称性[54]，也就是说每个费米面上都有s波对称的超导能隙打开，并且不同费米面上的超导序参量相位（或符号）相反。很快理论预言的铁基超导体中的多个费米面以及多个超导能隙在费米面上打开都被实验证实，例如，角分辨光电子能谱(ARPES)在最佳掺杂的Ba0.6K0.4Fe2As2中观测到了分别处在布里渊区Γ点和M点的多个空穴型和电子型的费米面，并且发现在超导态这些费米面上都有s波对称的超导能隙打开[16]。红外光谱[31,47]，扫描隧道谱[7,72]，比热[57]，点接触[61]等技术手段也观测到铁基超导材料中多个s波对称的超导能隙。然而由于没有相位敏感的实验报导，关于不同费米面上的超导序参量相位是否相反，我们无法获得直接的证据。

理论物理学家进一步指出，如果超导序参量不存在变号，即s++对称性，当Cooper对从一个s+的带被非磁性杂质散射到另一个s+的带时，Cooper对不会被拆开；而对于s±对称性，Cooper对从一个s+的带被非磁性杂质散射到一个s−的带时，就会被拆对，于是超导态的能隙中会出现大量的未配对准粒子[2,8]。红外光谱对超导能隙以及能隙中可能出现的未配对准粒子非常敏感，因此，可以用来研究铁基超导体中超导能隙对称性的问题。

Ba122体系的铁基超导体为我们提供了很好的研究对象。这个体系的母体是BaFe2As2。对母体进行空穴或电子掺杂，都会在FeAs面内诱导出超导电性。空穴掺杂的Ba1−xKxFe2As2是通过用K原子部分取代Ba原子得到的。由于Ba原子在FeAs面以外，我们称这种掺杂为面外掺杂。面外掺杂保持了FeAs面的完整性，没有在面内引入杂质，使得FeAs面比较干净。然而，电子型的Ba(Fe1−xCox)2As2则是利用Co原子部分取代Fe原子得到的，掺杂直接涉及到了FeAs面，因此称为面内掺杂。面内掺杂导致的晶体缺陷可以看做非磁性杂质，所以我们可以认为Ba(Fe1−xCox)2As2的FeAs面中存在大量的非磁性杂质。通过对比最佳掺杂的Ba1−xKxFe2As2和Ba(Fe1−xCox)2As2超导态的光谱响应，我们可以获得有关超导能隙对称性的重要信息[14]。

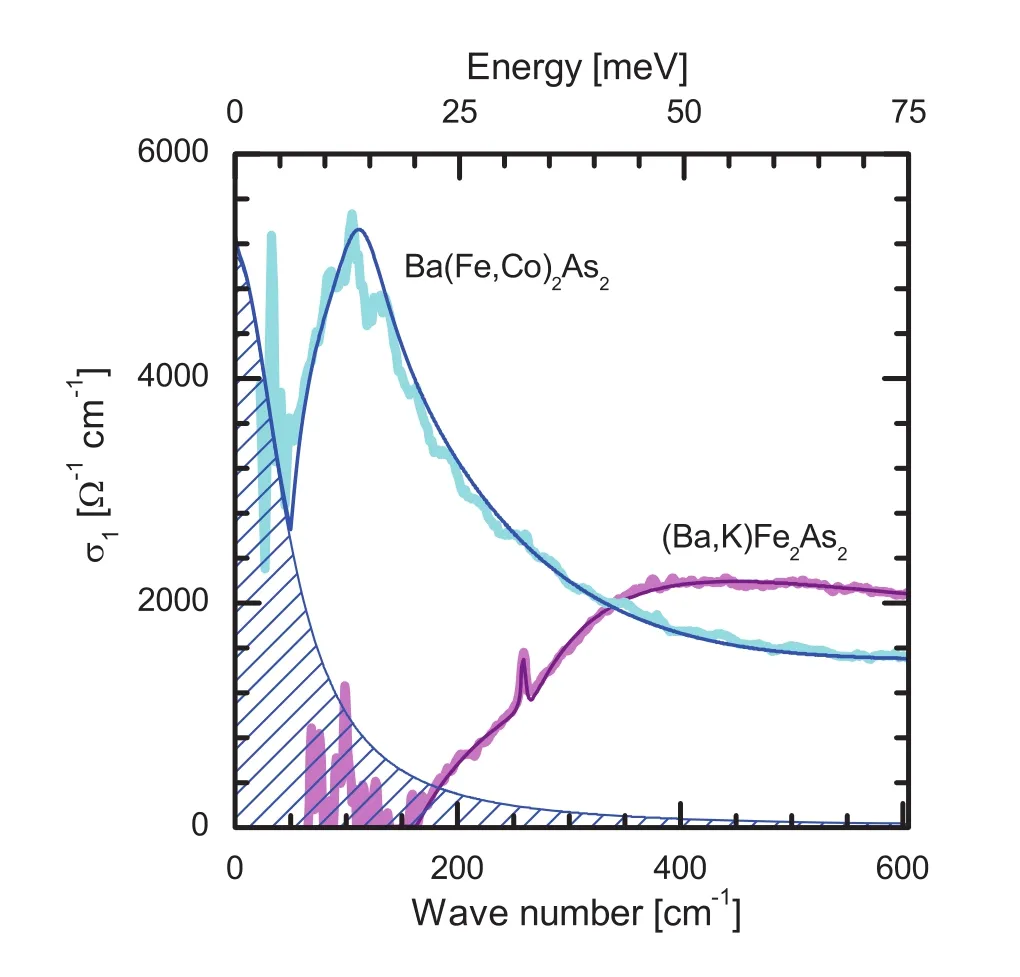
图8.5 K时最佳掺杂的Ba(Fe0.92Co0.08)2As2(Tc=25 K)和Ba0.6K0.4Fe2As2(Tc=38 K)的光电导谱。引自参考文献[14]。

图8比较了超导态下(5 K)最佳掺杂的Ba(Fe0.92Co0.08)2As2(Tc=25 K)和Ba0.6K0.4Fe2As2(Tc=38 K)的光电导谱。Ba0.6K0.4Fe2As2的光电导（粉色曲线）在大约160 cm−1以下降为零，表明超导能隙是s波对称的，能隙中不存在未配对的准粒子。而Ba(Fe0.92Co0.08)2As2的光电导（浅蓝色曲线）虽然在低频下出现了很陡的下降（表明超导能隙的打开），但是没有降至零。低频的光电导谱仍然需要一个Drude分量来描述（代表未配对准粒子），如图中蓝色阴影部分所示，这说明超导能隙中存在大量的未配对载流子。

以上实验现象再结合两个样品的特点，我们可以得出结论：Ba0.6K0.4Fe2As2属于面外掺杂，FeAs面比较干净，低能光电导谱上未观测到明显的未配对准粒子；而Ba(Fe0.92Co0.08)2As2属于面内掺杂，FeAs面内有大量非磁性杂质，低能光电导谱上出现了未配对准粒子导致的Drude响应。非磁性杂质拆对的事实支持铁基超导体中超导能隙对称性是s±。最近，南京大学的闻海虎科研小组利用准粒子干涉技术在(Li1−xFex)OHFe1−yZnySe中观测到非磁性杂质引起的带间散射拆对的实验为超导能隙的s±对称性提供了确凿的证据[21]。

B.自旋密度波能隙、赝能隙与超导的关系

我们知道，铁基超导体相图中的超导相通常出现在反铁磁相的边界处[53]，说明超导电性和反铁磁相有着密切的联系。然而，要想获得超导电性，又必须通过掺杂（或加压）来压制母体材料中的反铁磁相，并且随着反铁磁相的压制，超导临界温度逐渐提高，这又说明超导电性和磁性可能是竞争的关系。另外，铁基超导体中是否如铜氧化物高温超导体一样在欠掺杂区域存在赝能隙[17,90]，以及这个可能存在的赝能隙和超导电性是什么关系，都是超导研究领域急需解决的问题。以下部分我们讨论如何利用红外光谱来研究铁基超导体中的这些问题[13]。

我们选取了Ba1−xKxFe2As2欠掺杂的样品，其中K的掺杂浓度为x=0.2。这个样品的自旋密度波型反铁磁转变温度为TSDW=104 K，超导临界温度Tc=19 K。选取这个样品，一方面是因为这个掺杂范围内的样品反铁磁相和超导相在低温下是共存的，便于我们研究两者之间的相互关系。另一方面，考虑到铜氧化物高温超导体中赝能隙是在欠掺杂区域被观测到的，选取欠掺杂的样品便于我们研究铁基超导体中赝能隙是否存在，以及它和超导电性的关系是什么。

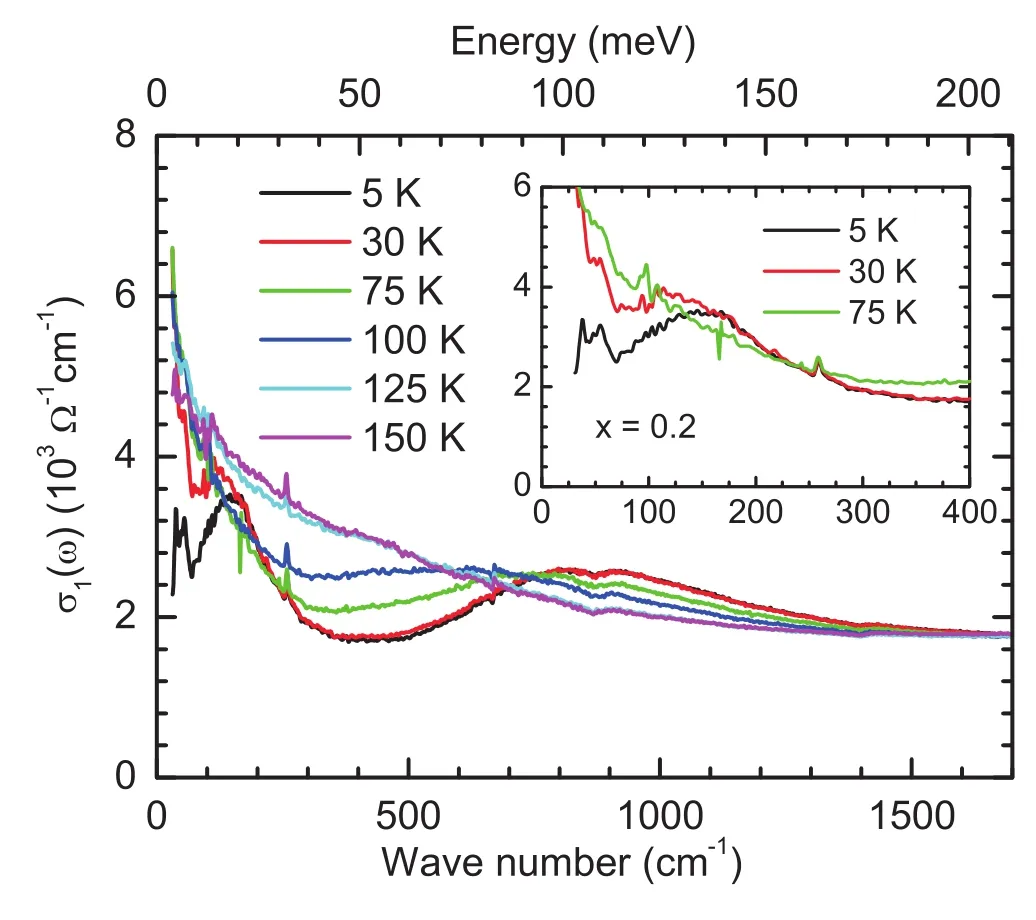
图9.欠掺杂的Ba0.8K0.2Fe2As2(TSDW=104 K；Tc=19 K)在不同温度下0∼1700 cm−1的光电导谱。插图中是5,30和75 K低频范围内(0∼400 cm−1)的光电导谱。

图9展示了Ba0.8K0.2Fe2As2在不同温度的光电导谱。在正常态下（150和125 K），低频光电导表现出明显的Drude行为，和材料的金属性一致。当温度低于TSDW=104 K时，400 cm−1附近的光电导谱被压制，并且随着温度的降低，谱线被压制地越来越低。同时，在700∼1500 cm−1范围内，光电导谱随温度的降低而升高。这是典型的自旋密度波能隙的光学响应[11,36]。这里，如果我们定义谱重为

其中，ωa和ωb分别为积分下限和上限，自旋密度波能隙的光学响应则可以描述为低频谱重向高频转移。另外需要说明，电荷密度波能隙和赝能隙具有相同的光学响应[34,92,95]。随着温度的进一步降低，我们发现在75 K以下，类似的低频光电导被压制，谱重转移到高频的现象再次发生在100 cm−1附近，表明又有个新的，能量更低的能隙打开（见图9插图中的红色30 K曲线）。这个新能隙打开的温度远低于自旋密度波相变温度TSDW=104 K，且远高于超导临界温度Tc=19 K，因此，可以推断这个能隙既不是自旋密度波能隙，也不是超导能隙。我们把这个100 cm−1附近打开的能隙称为赝能隙，其打开的温度表示为T∗≃75 K。当温度降至5 K时，如图9插图中的黑色曲线所示，低频光电导谱相对于30 K数据（红色曲线）进一步压低，表明超导能隙打开。

综上所述，我们在欠掺杂Ba0.8K0.2Fe2As2的光电导谱上观测到三个能隙。自旋密度波能隙在TSDW=104 K打开；赝能隙在T∗≃75 K打开；超导能隙在Tc=19 K以下，样品进入超导态打开。为了研究三个能隙或其对应的相之间的关系，我们需要进行细致的谱重分析。

图10给出了不同频率范围的谱重随温度的依赖关系。所有数据都已经相对于300 K数据进行了归一化。三条竖直的虚线分别表示Tc=19 K，T∗≃75 K和TSDW=104 K。蓝色的空心圆圈表示0∼12000 cm−1范围的谱重随温度的变化。注意这里计算的谱重已经包括了超导态凝聚到零频的超流密度。基本不随温度变化，是因为截止频率12000 cm−1已经足够高，覆盖了这个材料中相变涉及到的所有集体激发的能量范围，从而表现出谱重守恒的性质。红色的空心圆圈表示的温度依赖，0+表示计算谱重的积分未包含零频的信息。在TSDW陡然降低，这是由SDW能隙打开，将0∼650 cm−1范围的谱重压制并转移至高频所导致。在Tc附近的陡降是由超导能隙的打开进一步压制低频光电导谱所导致的。

绿色空心圆表示650∼1700 cm−1范围的谱重和温度的依赖关系。从光电导谱上可以看出，这个能量范围对应的是被SDW能隙转移到高频的谱重所处的范围。在高温区域(T>TSDW)，随着温度的降低而降低，这是由于金属性样品中的自由载流子散射率随着温度的降低而减小，光电导谱上的Drude峰变窄，从而导致谱重从高频区域(650∼1700 cm−1)逐渐向低频区域(0∼650 cm−1)转移。而在TSDW发生SDW相变，SDW能隙的打开将低频谱重向高频区域转移，这和金属性样品中自由载流子散射率降低导致的光学响应恰好相反，于是我们可以观察到TSDW以下，W1700650随温度的降低而升高。在Tc处，W1700650随温度变化的趋势未发生任何变化，这说明被SDW能隙转移至高频的谱重被保持在高频区域，而不参与超导凝聚，从而使可参与超导凝聚的谱重减少了。因此，我们可以认为Ba0.8K0.2Fe2As2中的SDW型反铁磁相和超导相是相互竞争的关系。

图10.Ba0.8K0.2Fe2As2不同频率范围内的光电导谱重随温度的变化。图中竖直的虚线分别表示Tc，T∗和TSDW。

赝能隙和超导电性的关系可以通过研究110∼250 cm−1范围的谱重随温度的变化来获得线索。如果一个赝能隙的起源是超导前驱，比如预配对，一旦长程的超导序形成，被赝能隙转移到高频的谱重会被转移至零频参与超导凝聚[38,92]。相反，如果一个赝能隙起源于某个和超导竞争的相，被赝能隙转移到高频的谱重则被保持在高频区域，而不参与超导凝聚，例如我们以上讨论的SDW能隙。由图10中的橙色空心圆可见，在T∗以上，表现出和类似的温度依赖：起初随着温度的降低而升高，在TSDW处由于SDW能隙的打开而陡然下降。然而在T∗处达到最低值后开始随着温度的降低而反弹，这是由赝能隙的打开所致。赝能隙的打开将110 cm−1以下的谱重压制，并转移到110∼250 cm−1范围内，从而导致在T∗以下，随着温度的降低而增加。有趣的是，温度低于Tc材料进入超导态的时候，突然降低。这表明由于赝能隙的打开被转移到高频区域的谱重参与了超导凝聚，这和超导前驱的情形是相符的。因此我们可以推断，Ba0.8K0.2Fe2As2中的赝能隙极有可能起源于和超导前驱有关的相，比如未发生相位相干的预配对。

C.非费米液体行为

在常见的非常规超导体的T−x相图中，例如重费米子超导体[26,52,80]，铜氧化物超导体[5,9,40]以及铁基超导体[18,27,29,51]等，超导相形成的拱形区域上方总是存在一个被称为“奇异金属”(Strange metal)或“非费米液体”(non Fermi liquid)的区域。在这个区域，材料正常态的电阻或载流子散射率随着温度的升高呈线性增加，严重偏离了朗道的费米液体理论对金属的描述（散射率或电阻呈T2变化）。由于非费米液体行为总是和最佳掺杂的超导电性同时出现，物理学家们认为非费米液体行为可能和高温超导具有相同的起源。大量的实验和理论的研究表明，如果利用非热学参数（如化学掺杂，压力或磁场等）将反铁磁相变温度压制到零温，我们可以得到一个反铁磁量子临界点(QCP)。这个反铁磁量子临界点附近的反铁磁自旋涨落非常强，以至于改变了准粒子的散射过程，导致了非费米液体行为的出现[56,77]。同时，反铁磁自旋涨落也可能是高温超导体中电子配对的机制[54−56,74,77]。然而，由于铁基超导体是多带材料[16,76]，至多5个Fe的3d轨道穿过费米能级，形成了多个费米面。不同费米面上的准粒子散射率以及对外界电场或温度的响应也可能各不相同，因此，材料的电输运性质变得非常复杂。铁基超导体中随温度线性变化的电阻究竟可不可以作为反铁磁量子临界点存在的证据？还是仅仅起源于这类材料的多带效应[67,69]？此外，在Ba122体系中，最佳掺杂的Ba(Fe1−xCox)2As2和BaFe2(As1−xPx)2正常态电阻在很宽温区内随温度均呈线性变化[18,22,43]，而最佳掺杂的Ba1−xKxFe2As2正常态电阻高温却趋于饱和，在175 K附近形成一个很宽的鼓包状特征[65,73]。这个鼓包是什么原因形成的？究竟非费米液体行为在铁基超导体中是否普遍存在？非费米液体行为的起源是什么？与超导配对机制又有着怎样的关系？在以下部分，我们将利用红外光谱对这些问题进行研究[12,15]。

图11.黑色粗线表示实验测量的Ba0.6K0.4Fe2As2在150 K的光电导谱；红色曲线是利用Drude-Lorentz理论模型拟合的结果，其中包括三个分量：粉红色区域表示窄Drude分量；蓝色区域表示宽Drude分量；高频的橙色区域表示Lorentz分量。插图中比较了拟合红外光谱得到的直流电阻率（红色空心圆）和输运测量的结果（蓝色实线）。

我们首先选取最佳掺杂的Ba0.6K0.4Fe2As2进行研究，以便更好的理解其正常态电阻行为。图11中黑色曲线表示Ba0.6K0.4Fe2As2在150 K的光电导谱。利用Drude-Lorentz理论模型对光电导谱进行拟合分析，我们发现这个材料的光电导主要来自三部分的贡献：一个窄的Drude分量（粉红色区域），一个宽的Drude分量（蓝色区域），再加一个Lorentz分量（橙色区域）。两个Drude分量和一个Lorentz分量分别描述材料中自由载流子和带间跃迁的光学响应。这三个分量的叠加（贯穿实验数据的红色曲线）可以非常漂亮的描述实验测量的光电导谱。在不同的温度重复以上的Drude-Lorentz拟合，我们发现这三个分量的叠加可以完美描述所有13个不同温度下测量的光电导谱。将拟合曲线零频的值提取出来再取倒数可以得到样品的直流电阻率 ρ≡1/σ1(ω→0)。图11插图中，我们比较了光电导谱拟合得到的结果（红色空心圆）和输运测量的结果（蓝色实线），发现两种手段获得的结果完全吻合。这说明我们的红外光谱测量准确，Drude-Lorentz拟合分析合理。低频光电导谱需要两个Drude分量来描述，说明Ba0.6K0.4Fe2As2中存在两类载流子，并且两类载流子具有不同的散射率。双Drude的分析方法在铁基超导体的光谱研究中已经被广泛接受[58−59,86]。

通过以上的Drude-Lorentz拟合分析，我们可以得到各个物理参数的温度依赖，如图12所示。其中下角标n和b分别表示窄的(narrow)和宽的(broad)Drude分量。(a)面板中显示两个Drude分量的等离子体频率Ωp都不随温度变化，表明两类载流子浓度以及有效质量都不随温度发生变化。(b)面板展示了两类载流子的散射率和温度的依赖关系。有趣的是，我们发现宽Drude的散射率随温度几乎不发生变化，而窄Drude的散射率随温度呈线性变化（图中的黑色虚线表示线性拟合），这正是高温超导体中常见的典型的非费米液体行为。说明非费米液体行为在最佳掺杂的Ba0.6K0.4Fe2As2也是存在的。为了进一步理解该材料正常态的输运性质，我们在(c)面板中画出了两个Drude分量的等效电阻。宽Drude的等效电阻（蓝色空心圆）不随温度变化，而窄Drude的等效电阻（红色空心方块）随温度线性变化，更有趣的是两者在大约175 K处相交，这个温度正好对应于电阻率曲线上鼓包的温度。两个Drude分量对直流电输运特性的贡献可以用简单的并联电路模型来描述[85]：σtotal=σn+σb。总电导率σtotal由电导率大的分量主导。在175 K以下，σn>σb(ρn<ρb)，直流输运性质由窄的Drude分量主导。因此，直流电阻率在低温下温度依赖明显，并且表现出接近线性的行为[73]。而在175 K以上，σn<σb(ρn>ρb)，直流输运性质由宽Drude分量主导，所以直流电阻率的温度依赖变缓，高温区域表现出饱和的趋势。175 K附近是过渡区域，故直流电阻率在此温度区域出现了一个鼓包特征。

以上结果表明，非费米液体行为也存在于最佳掺杂的Ba0.6K0.4Fe2As2。但是，表现出非费米液体行为的Drude分量和另外一个基本不随温度变化的分量并联对总的电输运性质产生贡献，导致该材料中的非费米液体行为在电阻率曲线上被多带效应掩盖，从而产生了175 K附近的鼓包特征以及高温趋向于饱和的性质。

为了进一步理解铁基超导体中的非费米液体行为的起源以及它和超导电性的关系，我们选取了系列Co掺杂的LiFe1−xCoxAs(x=0,0.06,0.12,0.26和0.4)进行更深入的研究[12]。在图13(a)中，我们利用同样的Drude-Lorentz理论模型拟合实验测得的不同掺杂组分LiFe1−xCoxAs的光电导谱，可以得到每个样品中窄Drude分量散射率和温度的依赖关系，如图13(b)-13(f)所示。对于每个Co掺杂浓度，我们用幂指数形式1/τ=1/τ0+BTα来拟合散射率和温度的依赖关系，拟合结果如图中红色曲线所示，这样可以得到不同掺杂浓度对应的幂指数α。我们发现在未掺杂的LiFeAs(x=0)中，散射率随温度呈T2变化，表现出费米液体行为，这和输运测量的结果是一致的[30,68]。幂指数α随着Co掺杂浓度的增加，逐渐减小。当x=0.12时，α具有最小值1.3，明显偏离费米液体行为。随着Co掺杂浓度的进一步增加，α开始回升，在x=0.4的样品中，α重新恢复至2，表明费米液体行为又重新出现，电阻率曲线也表现出完全相同的演化[12]。这说明LiFe1−xCoxAs中，随着Co掺杂浓度的增加，系统发生了费米液体–非费米液体–费米液体的连续过渡。

图12.通过在不同温度下进行Drude-Lorentz拟合得到的Ba0.8K0.2Fe2As2中各参数随温度的依赖关系。(a)等离子体频率；(b)散射率；(c)等效电阻。其中下角标n和b分别表示窄Drude和宽Drude分量；(b)和(c)中的黑色虚线表示线性拟合的结果。

图13.(a)蓝色曲线是实验测得的LiFeAs在100 K的光电导谱；红色曲线是Drude-Lorentz拟合的结果；光电导谱可以分解为3个分量：窄Drude分量（红色区域），宽Drude分量（绿色区域）和Lorentz分量（蓝色区域）。(b)-(f)展示了窄Drude的散射率随温度的变化。每个面板中的红色曲线是幂指数函数拟合的结果。引自参考文献[12]。

要理解LiFe1−xCoxAs中费米液体–非费米液体–费米液体过渡背后的物理，以及和超导电性的关系，必须借助其他实验手段。因此，我们利用核磁共振(NMR)测量了不同Co掺杂浓度样品的自旋–晶格弛豫速率1/T1T，可以反应低能自旋涨落的强度，并利用角分辨光电子能谱(ARPES)测量了每个样品的费米面结构。所有实验手段的测量结果全部总结在该系统的T−x相图中。如图14所示，相图背景颜色表示散射率或直流电阻率随温度变化的幂指数值，蓝色区域表示费米液体（幂指数为2），红色区域表示非费米液体（幂指数为1.3）。左下角的黄色区域表示超导相，橙色的实心圆表示超导临界温度Tc。绿色菱形代表的是NMR测得的20 K时自旋–晶格弛豫速率(1/T1T|T=20K)。插图中是拟合ARPES测量结果提取出来的不同Co掺杂浓度样品的费米面结构（左插图x=0，中间插图x=0.12，右插图x=0.4）。蓝色圆形表示Γ点附近的空穴型费米面；两个红色椭圆表示M点附近的两个电子型费米面。由整个相图可见，LiFeAs的费米面嵌套比较差，1/T1T|T=20K也比较低，表明低能的自旋涨落比较弱，此时系统表现出费米液体行为（左侧蓝色区域）。由于Co替换Fe属于电子型掺杂，随着掺杂浓度的增加，电子型费米面（两个红色椭圆）增大，而空穴型费米面（蓝色圆圈）减小。当x≃0.12时，电子型和空穴型的费米面大小相近，从而实现最佳费米面嵌套。此时1/T1T|T=20K达到峰值，表明低能自旋涨落大大增强，而样品的电阻率和散射率也明显地偏离了费米液体行为。随着Co掺杂浓度的进一步增加，电子（空穴）型费米面进一步增大（减小），最佳费米面嵌套被破坏，自旋涨落(1/T1T|T=20K)开始减弱，系统重新恢复到费米液体。相图左下角的超导相（黄色区域）随着x的增加Tc线性降低。

图14.LiFe1−xCoxAs的T−x相图。相图背景颜色表示用幂指数函数拟合散射率或直流电阻率随温度的变化得到的幂指数；菱形是用NMR测得的不同样品20 K时自旋–晶格弛豫速率；插图表示从ARPES实验测量提取出来的不同Co掺杂浓度样品的费米面结构；左下角的黄色区域表示超导相。引自参考文献[12]。

通过以上这些实验现象，我们可以得到两个重要结论：

1.LiFe1−xCoxAs中的非费米液体行为由低能的自旋涨落引起，而低能的自旋涨落是由费米面嵌套调制的；

2.伴随着低能自旋涨落增加，系统偏离费米液体，而超导相却被压制，说明至少在LiFe1−xCoxAs体系中，超导电性和非费米液体行为不具有相同的起源。

D.晶格振动，电–声相互作用

红外光谱还可以用来研究固体材料中的晶格振动（声子）以及声子和其他集体激发的耦合[32,87,88,91]，比如电子或自旋激发和声子的耦合（电–声耦合）等。在铁基超导体中，究竟电–声耦合在电子配对过程中扮演什么角色仍然存在争议。例如，一方面理论计算表明这类超导材料中的电–声耦合太弱，根本不足以支持如此高的超导临界温度[6]；另一方面，在SmFeAsO1−xFx和Ba1−xKxFe2As2中发现了很强的同位素效应[48]，说明电–声耦合可能对电子配对起到一定的作用。另外还有理论学家指出和Fe离子振动相关的电–声耦合可以引起很强的轨道涨落，而轨道涨落也可以作为电子配对媒介引起高温超导电性[45]。因此，研究铁基超导材料中的电–声相互作用或许对理解这类材料中的超导电性会有一定的帮助。下面我们利用红外光谱研究Ba122体系中不同掺杂方式对Fe-As声子模式以及电–声耦合的影响[87]。

图15.(a)BaFe2As2(BFA),Ba0.6K0.4Fe2As2(K40),Ba(Fe0.92Co0.08)2As2(Co08)以及BaFe2(As0.85P0.15)2(P15)在150 K的光电导谱。(b)在253 cm−1声子附近的放大图。贯穿数据点的黑色曲线是Lorentz模型拟合的结果；竖直的黑色虚线表示BFA中声子峰的位置。引自参考文献[87]。

图15(a)展示了Ba122体系的母体BaFe2As2(BFA)以及三种不同掺杂方式形成的样品Ba0.6K0.4Fe2As2(K40)，Ba(Fe0.92Co0.08)2As2(Co08)和BaFe2(As0.85P0.15)2(P15)在150 K的光电导谱。所有样品的光电导谱都表现出金属性的Drude行为，这已经在许多文章中讨论过[15,36,49,58,59,81]。258 cm−1附近的尖峰是Fe-As键振动对应的声子模式[1,70]。图15(b)是在声子峰附近的放大图，竖直的黑色虚线表示BFA中的声子峰位置。由该图不难发现，在K40样品中，K的掺杂使声子频率向低频移动（红移或软化），而在Co08和P15两个样品中，Co和P的掺杂均使声子的频率向高频移动（蓝移或硬化）。声子频率的变化通常和相关的原子之间的键长l变化紧密联系在一起：l增加，声子向低频移动；反之，l减小，声子向高频移动。由键长变化引起的声子频率移动可以用一个简单的公式来计算[28]。和BFA相比[66]，K40，Co08和P15的Fe-As键长分别缩短了0.3%[64−65]，0.5%[20]和0.8%[63]。由这些数据，以BFA为参照样品，我们可以计算出三种不同掺杂样品在150 K的声子频率。图16(a)中的空心菱形表示计算的结果。为了和实验结果进行对比，我们用Lorentz模型对所有样品150 K的声子进行拟合，可以准确得到声子的频率。实验结果在图16(a)中用实心方块表示。Co08和P15实验得到的声子频率和根据键长变化计算的结果符合的非常好，然而，K40实验得到的声子频率却严重偏离了理论计算的值。相对于BFA，K40的Fe-As键变短，理论上应该引起声子向高频移动，而实验测得的声子频率却极其反常地向低频移动。这说明K40中的声子很可能和电子发生了很强的耦合，导致声子的行为无法用简单的键长变化解释。电–声耦合导致声子频率红移的现象在双层石墨烯中被报导过[46]。

图16.(a)实心方块表示BFA以及三种不同掺杂方式样品中Fe-As声子模式在150 K的共振频率；空心菱形代表根据Fe-As键长变化计算的结果。(b)实心圆和实心三角分别表示声子线型的不对称度1/q2和共振强度Ω2。插图展示了扣除电子背景之后的声子线型，贯穿数据的黑色曲线是Fano模型拟合的结果。引自参考文献[87]。

电–声耦合的进一步证据可以从声子的线型上获得。在电–声耦合比较弱的情况下，声子表现出对称的线型，通常用Lorentz模型来描述。然而当电–声耦合很强时，声子会出现不对称的线型，这种不对称的线型可以用Fano模型描述[24,46]：

其中ω0，γ和Ω分别表示共振频率，线宽和强度。线型的不对称度用无量纲参量1/q2来描述。1/q2增大，表示Fano线型的不对称度增加，电–声耦合增强。当1/q2=0时，公式10变回线型对称的Lorentz形式。我们已经注意到，图15(b)中Lorentz模型可以较好的描述BFA，Co08和P15中的声子线型，而对K40中声子线型的拟合效果较差。在声子峰的右侧理论拟合和实验结果有明显的偏离。这说明K40中的声子线型出现了明显的不对称，因此应该使用线型不对称的Fano模型来描述。图16(b)的插图展示了四个样品中扣除电子背底之后的声子线型，可以看出K40（实心圆）的声子线型显然是不对称的。我们利用公式10给出的Fano模型对所有样品的声子线型进行拟合（黑色曲线表示拟合的结果），从而得到了线型不对称度1/q2。图16(b)中的实心圆表示不同样品中的1/q2。在BFA，Co08和P15中，1/q2≃0.0016小的可以忽略不计，而在K40中，1/q2≃0.045大约是其他样品的30倍。这说明K40中的电–声耦合远强于母体BFA以及其他两种掺杂方式的样品。此外，电–声耦合还会导致声子共振强度的增加[46]。通过以上Fano模型的拟合，我们还得到了声子共振强度Ω2，在图16(b)中用实心三角表示。和BFA相比，K40声子的Ω2几乎增加了一倍，而Co08和P15中 Ω2略有降低。由于声子共振强度正比于声子峰下的面积，其变化也可以直接从图16(b)插图中看出。Co08和P15中Ω2的小幅降低可能是面内掺杂引入的杂质引起的，而K40中Ω2的增加则是材料中存在很强电–声耦合的证据。

Co掺杂的Ba122体系Ba(Fe1−xCox)2As2最高Tc=25 K[22]，BaFe2(As1−xPx)2最高Tc=31 K[43]，而Ba1−xKxFe2As2的最佳Tc可以达到38 K[65,73]。或许K40中增强的电–声耦合对更高的Tc也是有贡献的。

VI.总结

本文首先介绍了傅立叶变换红外光谱仪的基本原理，以及如何利用原位镀膜技术准确测量固体材料的绝对反射率，然后介绍了如何利用Kramer-Kronig关系从实验测量的反射率谱计算凝聚态物理研究中人们最关心的光电导谱，以及研究中常用到的Drude和Lorentz色散理论模型，最后以近几年发表的文章为基础，详细讨论了如何利用红外光谱对铁基超导材料中的重要问题进行研究，其中包括：(1)通过比较面外掺杂的Ba0.6K0.4Fe2As2和面内掺杂的Ba(Fe0.92Co0.08)2As2在超导态的光电导谱，我们发现面内掺杂引入的非磁性杂质可以拆开Cooper对，导致了低能剩余光电导的出现，为铁基超导体能隙的s±对称性提供了证据[14]。(2)在欠掺杂Ba0.8K0.2Fe2As2的光电导谱上发现了赝能隙，并利用光电导谱重分析，证明了在这个材料中磁性和超导电性是竞争关系，而赝能隙可能是超导的前驱[13]。(3)在最佳掺杂的Ba0.6K0.4Fe2As2中，通过研究光电导谱的详细温度依赖，发现了隐藏的线性温度依赖的散射率（非费米液体行为），这个现象被该材料中的多带效应所掩盖，导致无法从电阻率随温度变化的曲线上直接观测到[15]。利用同样的方法，在系列掺杂的LiFe1−xCoxAs中发现了费米液体–非费米液体–费米液体的连续过渡行为，并结合ARPES和NMR-等手段证明该体系中的非费米液体行为是费米面嵌套调制的低能自旋涨落引起的，且非费米液体行为在该体系中和超导电性可能具有不同的机制[12]。(4)通过比较Ba122体系的母体BaFe2As2以及三种不同掺杂方式形成的样品Ba0.6K0.4Fe2As2，Ba(Fe0.92Co0.08)2As2和BaFe2(As0.85P0.15)2光电导谱上的声子行为，发现K掺杂的Ba122体系中增强的电–声耦合效应，而这个增强的电–声耦合效应可能和Ba1−xKxFe2As2体系具有最高Tc相关[87]。

致谢

作者感谢南京大学的闻海虎教授、中国科学院物理研究所的邱祥冈研究员，法国巴黎市立高等物理化工学院(ESPCI)的Ricardo Lobo研究员、美国布鲁克海文国家实验室(BNL)的Christopher Homes研究员以及瑞士University of Fribourg的许兵博士的讨论和帮助。