基于灰靶理论和磨粒浓度的磨损状态自动识别

王庆维，王静秋

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

磨损、腐蚀和疲劳是三种导致机械零部件失效的主要原因，而三者中磨损一项占了八成左右[1]。磨损不仅会消耗材料与能源，也会影响机械设备的可靠性。零件的磨损也会造成机械设备的工作效率和精度变低，导致能耗增加以及漏油、漏气、噪声等故障发生的概率增大。因此对机械设备进行监测，确定设备异常磨损的部位以及故障发生的原因，及时地对设备进行保养维修，避免故障的发生，减少停机造成的损失并保证工作人员的安全，对设备进行磨损工况监控和故障诊断都具有重要的意义。

在众多设备状态检测和故障诊断方法中，油液检测技术作为一种有效的工况监测方法已在各类机械设备上得到广泛的应用。由于铁谱图像的复杂性，油液分析技术往往需要有经验的技术人员，凭经验来判断机械的磨损状态，不能做到磨粒的自动化识别[2]和设备磨损的自动判断。于是在自动分析只能得到少量数据的情况下，灰色系统理论得到了应用。目前已有学者利用灰色关联方法对磨损模式进行判别。而监测过程中，设备运行往往没有标准模式，因此本文引入灰色系统理论中灰靶理论进行分析研究。

1 灰靶理论原理

灰靶理论(grey target theory)即灰模式理论是邓聚龙教授提出的[3-6]，用于处理模式序列的灰关联分析理论。

灰靶理论的计算是在没有标准模式的条件下构造一个灰靶，即在任意的一组模式序列中，找出最靠近子命题目标值的数据构造标准模式，然后各待测模式与标准模式一起构造灰靶，则标准模式便是灰靶的靶心。然后将每一个指标的模式与标准模式进行比较，求出灰关联度，最后由划分的等级来确定评估等级。

灰靶理论包括两部分：靶心度分析和贡献度分析。靶心度计算步骤为：建立设备的标准故障模式；进行灰靶变换；计算灰关联系数；计算靶心度；待识别模式的识别。灰靶贡献度就是研究各性能指标对靶心度大小的影响。

1.1 靶心度计算

如果用序列来表示设备在i时刻的n个状态参数值，那么称该序列为设备状态模式。基于灰靶理论分析方法，根据设备在m个时刻的故障状态，建立设备的标准故障模式，然后将待识别的设备状态模式{ωi(1)，ωi(2)，…，ωi(n)}与设备的标准故障模式进行关联度分析，进而识别该设备的故障模式。

1) 建立标准故障模式ω0

设ωi为设备的第i次故障模式，ω(k)为设备状态监测的第k个状态参数序列，则按如下建立标准故障模式ω0。

ωi={ωi(1),ωi(2),…,ωi(n)}，

∀ωi(k)∈ωi⟹k∈{1,2,…,n}，

i∈I={1,2,…,m}；

ω(k)={ω1(k),ω2(k),…,ωm(k)}，

∀ωi(k)∈ω(k)⟹i=I∈{1,2,…,m}。

令POL(max)，POL(min)，POL(mem)分别为极大值性、极小值性和适中性极性。

那么称序列ω0={ω0(1),ω0(2),…,ω0(n)}

为设备的标准故障模式。

2) 灰靶变换T

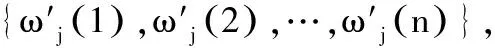
(1)

式中：j=J∈{1,2,…,P}，P是待识别的状态模式总数。

当j=0时，有：

Tω0=x0={x0(1),x0(2),…,x0(n)}={1,1,…,1}

称x0为标准靶心。

3) 灰关联系数γ{x0(k),xj(k)}

(2)

式中：

Δ0j(k)=|x0(k)-xj(k)|=|1-xj(k)|，

j∈J={1,2,…,P}，k∈K={1,2,…,n}，ρ=0.5

4) 靶心度计算γ{x0,xj}

(3)

5) 设备状态模式识别

按最小信息原理，靶心度的分档应该均衡分布，所以有[0.1，0.2]，[0.2，0.3]，[0.3，0.4]，[0.4，0.5]，[0.5，0.6]，[0.6，0.7]，[0.7，0.8]，[0.8，0.9]， [0.9，1] 。

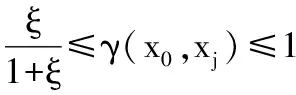
取ξ=0.5，则γ(x0,xj)≥0.333 3

所以，0.333 3以下各档无意义。根据设备故障的描述系统，对设备故障的描述可分为：正常磨损、轻微磨损、严重磨损、磨损十分严重。于是将靶心度分为如下等级：

γ(x0,xj)=1，理想状态，该设备完全正常；

γ(x0,xj)=[0.8，1]，正常磨损；

γ(x0,xj)=[0.7，0.8]，轻微磨损；

γ(x0,xj)=[0.5，0.7]，严重磨损；

γ(x0,xj)<0.5，磨损十分严重。

最后根据xj的靶心度γ(x0,xj)的大小，计算出设备在时刻j的状态与标准状态模式的接近程度，从而进行设备运行状态判断。

1.2 灰靶贡献度

模式由指标构成，模式的靶心度大小与指标有关。所谓灰靶贡献度就是研究各性能指标对靶心度影响程度的一种数学方法[7]。

令@GRF为灰关联因子集，

@GRF={x(k)|k∈K∪{0},K={1,2,…,n},

x(0)=(x1(0),x2(0),…,xm(0)),

∀xi(0)∈x(0)⟹xi(0)=Tlωi(0),

Tu、Tl和Tm分别为极大值性、极小值性和适中性极性。称x(k)为第k个贡献因子，称@GRF为贡献因子集。

令ΔGR为贡献因子集对应的灰关联差异信息空间，

ΔGR=(Δ,ζ,Δmax(0,k),Δmin(0,k))，

Δi(0,k)=|xi(0)-xi(k)|，

则ΔGR上的灰关联系数γ(xi(0),xi(k))：

(4)

称为k指标在i点(模式)的贡献系数；

灰关联度γ(x(0),x(k))：

(5)

称为k指标的贡献度。

1.3 加权公式的构造

在求得各指标的灰靶贡献度后，取它们的平均值并记做γmem。则该值所对应的权值应为1/n。以各指标贡献度与贡献度平均值的差为依据，构造如下公式，通过差值所占平均值的比例来确定权值。

(6)

式中，当γ(i)>γmem时，取正号；当γ(i)<γmem时，取负号。

最后引入加权系数之后的靶心度计算公式为：

(7)

2 基于灰靶理论和磨粒浓度的磨损状态的自动识别

2.1 磨粒浓度的获取

铁谱分析技术是一种通过分析铁谱图像的磨粒尺寸、数量、形貌和成分等特征[8-9]去识别机械状态的技术。在众多特征中，磨粒尺寸和数量是图像自动化处理最容易得到的，同时也是最直观反映设备磨损状态的特征。

磨粒尺寸指的是磨粒长轴尺寸。长轴为图1磨粒等效椭圆图中的a。于是可以通过等效椭圆的方法，得出磨粒的尺寸。

图1 磨粒等效椭圆图

首先确定磨粒中某个像素点所处磨粒的尺寸，然后把该像素点加入到对应的尺寸范围内，通过该方法得到所有磨粒中像素点的尺寸范围，并计算出各尺寸范围的磨粒浓度。以各尺寸的磨粒浓度为指标建立标准模式。磨粒浓度为铁谱图像中各尺寸范围内的磨粒面积与总磨粒面之比。

本文的分析对象为某公司型号Y7001的设备。表1为6幅铁谱图像通过上述的方法得出的磨粒浓度表，通过表1建立标准模式，来识别表2中的待检测铁谱图像的磨损状态。图2和图3为该设备的不同时间的铁谱图像，对应着表2中的样本1和样本2的磨粒浓度。通过图2和图3，知道图2设备所处的时间，图像中都是比较小的磨粒，没有出现较大磨粒，所以认为设备为正常磨损，只需要继续监测设备状态。而图3的图像中不仅有较小的磨粒，而且出现了较大的磨粒，或者说设备出现了不异常磨损，需要对设备进行检查和维修。

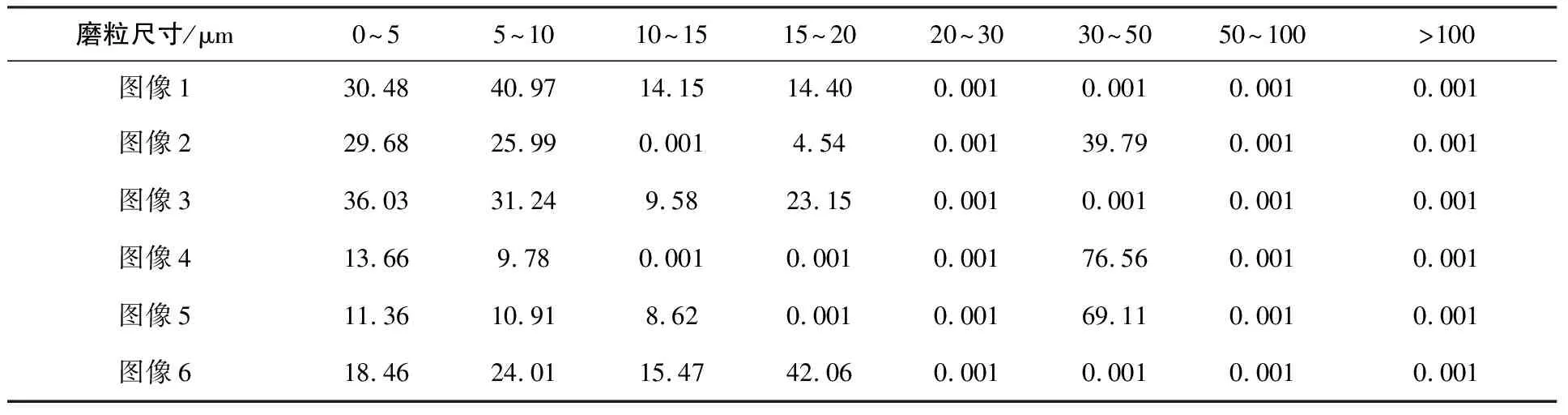
表1 标准模式的磨粒浓度表

表2 待检测图像磨粒浓度表

图2 样本1图像

图3 样本2图像

2.2 靶心度计算

1) 建立标准模式

ω0(1),ω0(2),ω0(3)采用POL(mem)，其余使用POL(min)。

ω0(1)=avg{30.48,29.68,36.03,13.66,11.36,18.46}=23.28

同理：ω0(2)=23.82ω0(3)=7.97

ω0(4)=0.001ω0(5)=0.001

ω0(6)=0.001ω0(7)=0.001

ω0(8)=0.001

则标准模式：

ω0={ω0(1),ω0(2),…,ω0(8)}={23.28,23.82,7.97,0.001,0.001,0.001,0.001,0.001}

2) 灰靶变换

对待识别模式进行灰靶变换。

(8)

根据式(1)计算可得:

{0.338 3，0.971 0，0.834 8，1，1，1，1，1}

{0.464 6，0.297 8，0.899 2，1，0，0，1，1}

3) 靶心系数及靶心度的计算

样本1：

γ{x0(1),x1(1)}=0.333 3

γ{x0(2),x1(2)}=0.919 5

γ{x0(3),x1(3)}=0.667 0

γ{x0(4),x1(4)}=1

γ{x0(5),x1(5)}=1

γ{x0(6),x1(6)}=1

γ{x0(7),x1(7)}=1

γ{x0(8),x1(8)}=1

靶心度：

样本2：

γ{x0(1),x2(1)}=0.482 9

γ{x0(2),x2(2)}=0.415 9

γ{x0(3),x2(3)}=0.832 3

γ{x0(4),x2(4)}=1

γ{x0(5),x2(5)}=0.333 3

γ{x0(6),x2(6)}=0.333 3

γ{x0(7),x2(7)}=1

γ{x0(8),x2(8)}=1

靶心度：

2.3 灰靶贡献度

根据表1，得出贡献因子集由8个序列构成：

ω(0)=(ω1(0),ω2(0),…,ω8(0))={1,2,3,4,5,6}

现给出参照表1所得磨粒各尺寸的贡献度：

γ=(0.613 6,0.697 7,0.670 9,0.670 9,0.478 7,0.642 4,0.478 7,0.478 7)

2.4 加权公式构造

根据式(6)，经计算所得的权值为:

q1=0.129 6，q2=0.147 4，q3=0.141 8，q4=0.141 8，

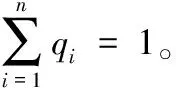
样本1：

样本2：

通过样本1和样本2的靶心度与设备状态级比较，可知设备在样本1的靶心度所处的范围为γ(x0,xj)=[0.8，1]，所以设备磨损状态为正常磨损；而设备在样本2的靶心度所处的范围为γ(x0,xj)=[0.5，0.7]，所以设备磨损状态为轻微磨损状态。由样本2的靶心度，可预测设备出现了异常的磨损情况，建议对设备的该时刻之后进行检测。实验得出的结果与设备实际检测的情况是一致的。

3 结语

本文基于灰靶理论和磨粒浓度的磨损状态的自动识别，经算例分析验证了其有效性，可应用于设备磨损状态的自动识别。通过分割算法得到准确的铁谱图像的各尺寸磨粒浓度，为模型提供了准确的数据依据；利用贡献度优化指标权重，考虑不同的尺寸浓度的影响，考虑的因素更加全面，也证明了靶心度能反映设备的磨损状态。本文基于灰靶理论和磨粒浓度的磨损状态的自动识别，实现了从铁谱图像到设备磨损状态的自动识别，对实际的决策评估过程具有一定的指导和借鉴意义。