基于单粒子模型的锂离子电池荷电状态估计
2018-08-21崔鹰飞陈则王
崔鹰飞,陈则王
(南京航空航天大学 自动化学院,江苏 南京 211106)
0 引言
在能源危机和环境污染日益严重的背景下,节能和环保是时代的主题,寻求安全、清洁、高效的能源转化和存储技术是目前科技领域的研究热点。电池作为一种电能的存储和转化载体,能够在几乎不付出环境污染代价的同时以极高的效率转化能量,因而受到科技领域的广泛关注。荷电状态估计(state of charge, SOC)是电池管理系统的核心部分,它不仅可以使用户直观明确地了解电池电量的使用及剩余情况,还决定着电池的使用性能和安全。由此可见,电池SOC的估算研究有着重要的意义[1]。
目前常用的SOC估计方法大多是基于电池模型实现的。将模型应用于电池管理系统当中,不仅要考虑模型的准确性,使模型尽量准确地还原电池的工作情况,还要考虑模型的简便程度,以使模型的计算合理占用资源,提高效率[2]。常用的电池模型主要有经验模型[3]、等效电路模型[4]、神经网络模型[5]和电化学模型。经验模型、神经网络模型的精度受限于训练样本,而等效电路模型中的模型参数并没有实际物理意义,在复杂工况上误差较大,且这3种模型都无法分析电池的老化和安全问题。而电化学模型从机理上分析电池特性,模型精度更高。
常用的电池电化学模型有准二维多孔电极模型(P2D model)和单粒子模型 (SP model)。P2D模型[6-7]包含一系列耦合偏微分方程,模型复杂度很高,不适合直接应用于电池管理系统。
SP模型[8-9]就是利用单个粒子来代替活性物质中的所有粒子,忽略了电解液浓度梯度、液相扩散过电势、固相浓度在电极厚度方向上的浓度分布,并假设各电极内电化学反应均匀,各点反应率完全一致,从而减少了偏微分方程的个数,使计算过程得到简化。单粒子模型与P2D模型相比,计算过程得到简化,在中低倍率下能较好地描述电池工作状态。
由于实际应用中仍然存在需要中低倍率工作的电池,如手机等。本文选用单粒子模型来对电池建模,通过单粒子模型即可根据电池工作电流求解出相应时刻的电池端电压和活性粒子内平均浓度cs,avg,i,而电池SOC可以通过活性粒子内平均浓度进行求解。因此可以通过单粒子模型得出电池端电压与电流以及SOC的关系方程,将该方程作为扩展卡尔曼滤波的观测方程,采用扩展卡尔曼滤波算法实现SOC的在线估计,最后基于COMSOL的仿真数据来分析SOC估计的精度。
1 锂电池电化学模型
1.1 伪二维多孔电极模型
锂电池内部结构如图1所示,主要由正极集流体、正极活性材料、隔膜、负极活性材料、负极集流体、电解液组成[2]。假设活性粒子为球形颗粒,锂离子在活性粒子中沿着r方向扩散,这是锂离子的固相扩散过程。对于锂离子在电解液中的迁移,即液相扩散过程,伪二维多孔电极模型只考虑x方向上锂离子的迁移。总的来说,伪二维多孔电极模型由10个耦合的非线性偏微分方程组成。
简单来说,准二维多孔电极模型即可以根据电流输入来模拟仿真得出对应时刻的电池端电压、相关锂离子浓度等信息。由于在锂电池电化学建模领域存在相关参数获取困难的问题,一般通过将P2D模型仿真结果作为一个参考值来验证其他简化模型的精度高低,因此本文将准二维仿真得到的端电压以及基于准二维模型采用安时积分法求出的SOC作为参考值来验证本文提出的SOC估计算法的准确性。具体的控制方程见表1。相关参数见表2(参数来源于COMSOL仿真软件以及文献[6])。

表1 伪二维数学模型各区域的控制方程及边界条件
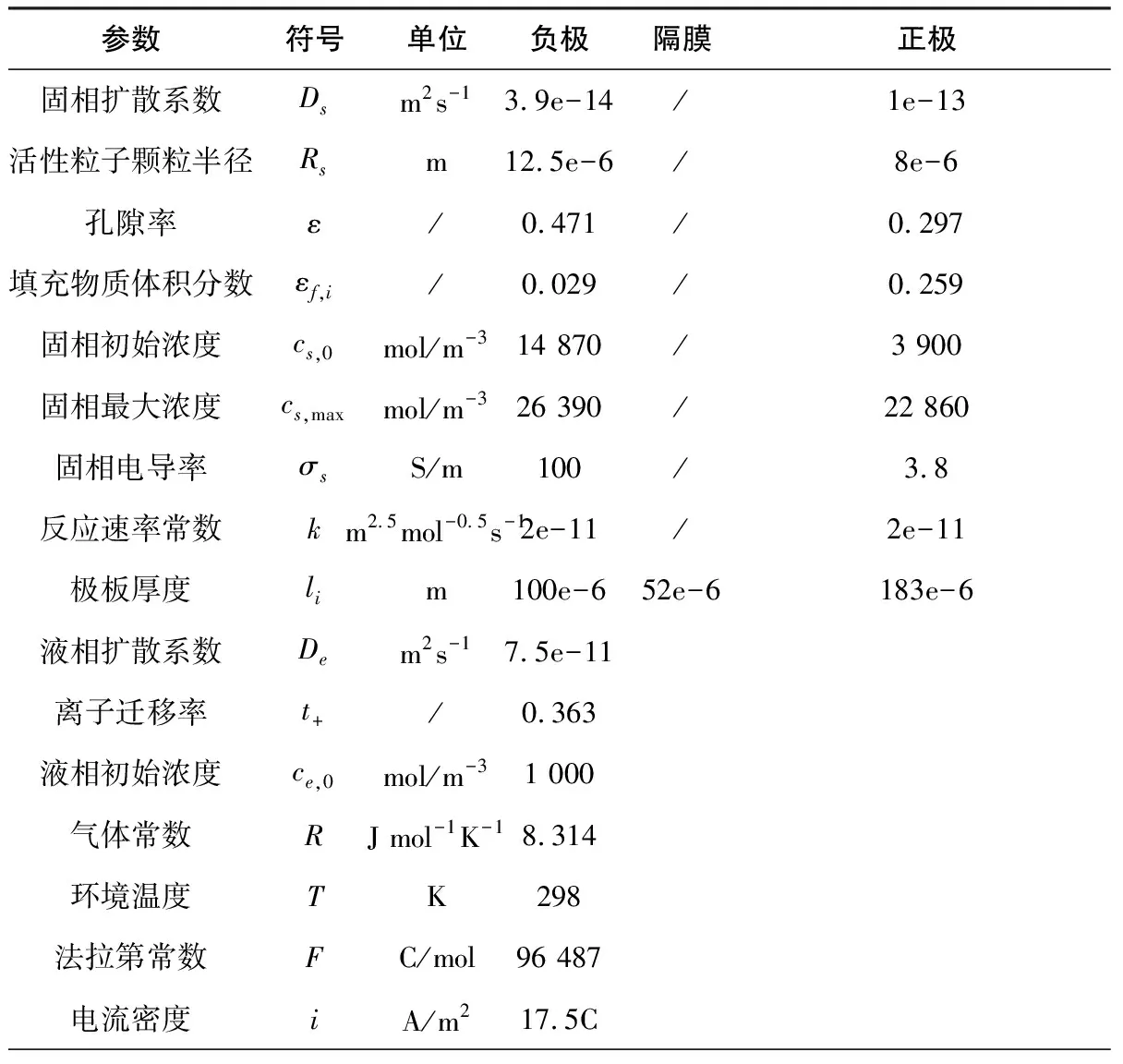
表2 电池模型参数

续表2
1.2 单粒子模型
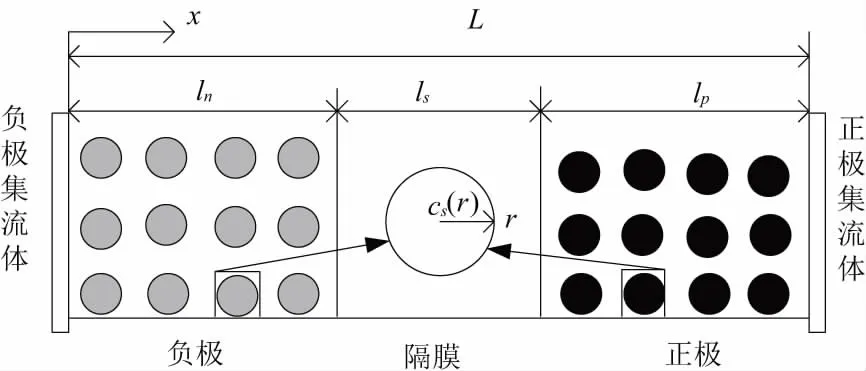
图1 锂电池结构原理示意图
单粒子模型指的是利用一个球形粒子来代表整个电极而建立的一种电池简化数学模型。建立电池单粒子模型的第一个前提条件是假设整个电池内(正极、隔膜和负极)各处的液相浓度值均是一个常量;另一个前提条件是假设一个电极内各处的固相电势相等。基于这些假设条件可知一个电极内各处的反应离子流密度也相等,这样电极内一个活性粒子的电化学特性就可以代表整个电极的特性,进而得到了电池的单粒子模型。由于单粒子模型假设电极内各处的反应离子流密度相等,则正负极集流体边界处的反应离子流密度为:
(1)
式中:I为电池工作电流,放电为正,充电为负,A为电极有效面积;Ri为活性粒子颗粒半径;li为极板厚度;εi为材料孔隙率;εf,i为填充物质体积分数;F为法拉第常数;p为正极,n为负极。
这里利用三参数抛物线近似法[10]来简化固相扩散过程,进而求解得到固相粒子表面锂离子浓度。则粒子表面锂离子浓度可以通过下式近似求解。
(2)
(3)
式中:cs,avg,i为正负极活性粒子内平均锂离子浓度;cs,0,i为固相初始锂离子浓度;Ri为正负极活性粒子颗粒半径;ji为正负极反应离子流密度;cs,surf,i为正负极活性粒子表面锂离子浓度;Ds,i为正负极固相扩散系数;qi,avg(t)为是固相扩散过程中粒子内锂离子体积平均浓度流量;n为负极区域,p为正极区域。
在恒流放电工况下,qi,avg(t)的计算式为:
(4)
(5)
在其他任何充放电工况下,qi,avg(t)的计算式为:
(6)
活性粒子的表面浓度决定了锂电池的开路电压,如式(7)所示。
(7)
式中:UP为正极开路电压,Un为负极开路电压。根据Bulter-Volmer方程,可以推导出反应极化过电势如式(8)所示。
(8)
(9)
在单粒子模型中,认为电池的欧姆极化过电势主要是SEI膜欧姆极化过电势。欧姆极化过电势表示为:
ηSEI=RSEI,pFjp-RSEI,nFjn
(10)
则电池端电压可以表示为:
U=Up(cs,avg,p)-Un(cs,avg,n)-ηact-polarzation-ηSEI
(11)
本文将SOC定义为:
(12)
(13)
(14)
式中:cs,avg,i为正负极固相平均锂离子浓度;cs,max,i为正负极固相最大锂离子浓度;θ100%为荷电状态为100%时的化学计量比;θ0%为荷电状态为0%时的化学计量比;n为负极;p为正极。
则式(11)可以记为:
V=Up(SOC)-Un(SOC)+f(C)
(15)
式中C为放电倍率。
2 基于EKF的锂离子电池SOC估计方法
2.1 安时计量法
通过对运行时间内流过电池的电流进行积分,计算出流入或者流出电池的电量,如果已知电池的初始SOC值,便可用初始SOC值加上或者减去流过电池的电量,得到电池剩余电量。
本文基于安时积分法估计出的SOC作为SOC参考值,如式(16)所示。
(16)
式中Ck为k时刻放电倍率。
2.2 基于EKF的SOC估计方法
卡尔曼滤波算法通过采用递推线性最小方差估计方法,利用系统可观测的输出估计误差去修复不可观测的状态估计误差。卡尔曼滤波主要用于估计线性时变模型,而当被估计的系统模型是非线性的时候,就需要使用扩展卡尔曼滤波来对系统进行估计。卡尔曼滤波是一个递推的过程,而本文采用卡尔曼滤波,则可以根据电流量输入依次递推求解相应时刻的SOC值,即可实现SOC的在线估计。
锂离子电池SOC在线估计的离散空间状态方程与观测方程如式(17)、式(18)。
(17)
Vk=Up(SOCk)-Un(SOCk)+f(Ck)+νk
(18)
式(17)为状态方程,可以记为:
xk=f(xk-1,uk-1)+wk
(19)
式(18)为观测方程,可以记为:
Yk=h(xk,uk)+vk
(20)
式中:xk是状态变量(SOC),Yk是观测量(端电压),uk是输入量(充放电倍率),f和h是传递函数,wk与vk分别是系统噪声和观测噪声,默认为互不相关高斯白噪声。
定义:
xk=SOCk
(21)
uk=Ck
(22)
(23)
(24)
(25)
EKF滤波算法的循环递推计算如下:
1) 初始化状态变量x0和协方差P0
x0=E[x(0)]
(26)
P0=E[(x(0)-x0)(x(0)-x0)]
(27)
2) 状态预测
(28)
3) 观测预测
Yk=h(xk,uk)
(29)
4) 求协方差矩阵预测
(30)
5) 求Kalman增益
(31)
6) 状态更新
(32)
7) 协方差更新
(33)
3 仿真验证与分析
由于单粒子模型在中低倍率工况下精度高,因此本文选取0.2C恒流放电工况和0.5C恒流放电工况来验证本文所提出的SOC估计算法的有效性。由于安时积分法在初始值准确的情况下求出的SOC是准确的,仿真实验已知电池初始SOC,因此可采用安时积分法求出的SOC当做真实值,来对本文提出的SOC估计方法的精度进行比较分析。而另外安时积分法又不存在修正能力,本文又对初始值存在误差情况下的安时积分法求解出的SOC与本文提出的方法进行了比较,来分析本文提出的SOC估计方法的误差修正能力。SOC估计曲线和曲线细节图如图2-图4所示。
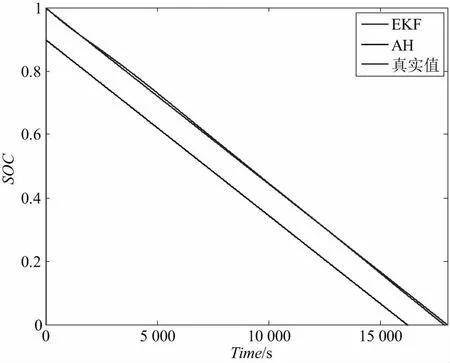
图2 初始SOC存在0.1误差下0.2C恒流放电工况SOC估计曲线
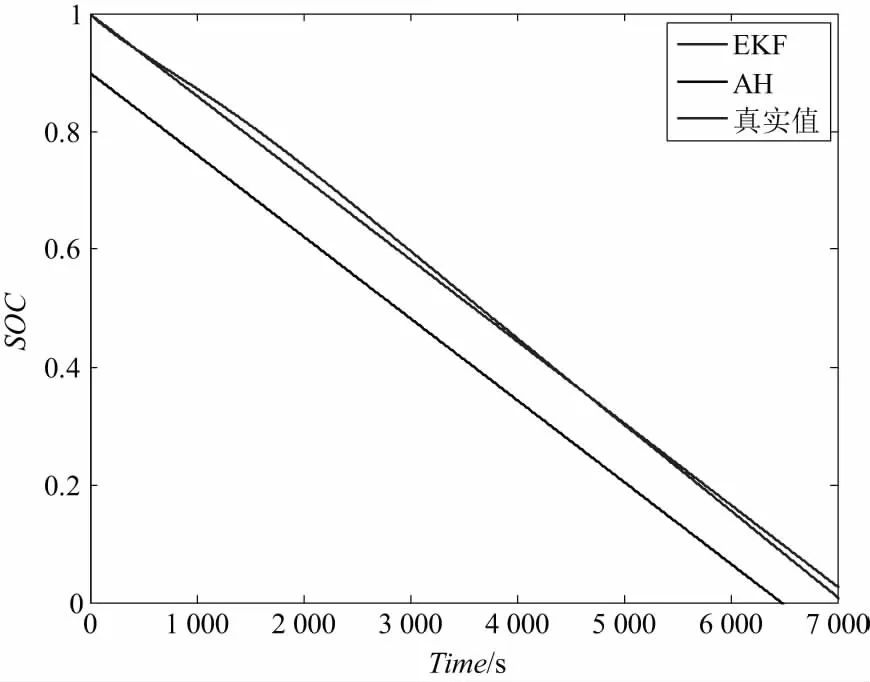
图3 初始SOC存在0.1误差下0.5C恒流放电工况SOC估计曲线

图4 初始SOC存在0.1误差下0.5C恒流放电工况SOC估计曲线细节图
从图2和图3可以看出,本文所采取的SOC估计算法精度较高,且有一定的误差修正能力。当SOC初始值存在10%的误差情况下,AH法严重偏离真实值,而本文采取的扩展卡尔曼滤波法能够较好修正SOC值。从图4可以看出,EKF递推到第4步时SOC误差<2%。
4 结语
1) 在电池单粒子模型的基础上,采用扩展卡尔曼滤波实现SOC在线估计,精度较高。
2) 当SOC初始值不准确时,本文采用的扩展卡尔曼滤波法具有很好的鲁棒性,能够准确地校正SOC,使之回归真值附近。
