基于变空阻虑风射流模型水炮俯仰角度的确定方法
2018-08-21李明赵敏肖辉陈皓
李明,赵敏,肖辉,陈皓
(南京航空航天大学 自动化学院,江苏 南京 211106)
0 引言
高压射流水炮在消防、海监领域均获得了广泛的应用。水炮俯仰角度的研究受到了广泛关注。目前主要有以下3种基本研究方法:1) 将水炮射流的一段流体微团作为研究对象,认为空气阻力与速度成正比,以此建立理论模型进行求解。由于采用了修改指数和类比使得计算复杂,实用性较差;2) 以射流雾滴作为抛射体来模拟射流轨迹,同时认为空气阻力系数保持不变。通过实验与计算发现,理论数据与实际数据相差较大;3) 考虑水炮射流的截面积变化,通过运动方程模拟水射流轨迹,但是误差相对较大。以上3种方法考虑因素不够全面、空气阻力计算不够准确、模型建立不够完善,导致得到的理论数据与实际数据相差较大,而且计算复杂。鉴于目前的大流量高压水炮俯仰角度确定都不太准确,本文综合考虑风力、空气阻力、重力、浮力等影响因素,建立一套射流理论模型,综合分析射流初速度、炮口压力、射流流量、炮口直径等因素对射程的影响。参照外弹道学理论确定水炮射流质点所受空气阻力,通过传感器测定风速风向,将风力矢量考虑到射流理论模型中,通过实验采集、存储数据,比较真实数据与理论数据的误差,分析得到的误差是否在合理的范围内。针对应用于海监船的高压射流水炮,将目标相对海监船的距离作为水炮应有的射程,通过理论模型得到此射程对应的水炮俯仰角度。控制模块通过PLC控制电机转动,进而控制水炮转动相应的空间俯仰角度。
1 水炮射流模型
水炮射程的影响因素众多,大致可分为3类:1) 初始参数,即射流初始速度、射流初始仰角,而射流初速度由水炮压力和流量决定[1],这是主要因素;2) 外界因素,如风的影响,大气压的影响等;3) 结构参数,水炮的机械结构性能使得炮口射流存在涡旋与速度梯度,对于水炮射程的有一定影响,但是影响相对较小。
水炮射流运动过程:射流离开炮口时,初速度一般较大,此时认为水炮射流基本不产生破粹现象,仍以完整水柱形式向前近似直线运动;当运动一段时间后,其所受空气阻力、风力等影响显著,大于其表面张力,使得水炮射流产生破粹现象,产生水滴,将以抛物线形式运动;最后将以略微散裂的水柱形式陡降冲击击打目标。
1.1 射流质点受力分析
选取水炮射流中的单位体积、单位流量的微元作为研究对象,以水炮每秒喷射的水道作为研究质点进行受力分析。在标准大气压下,正常户外温度时,水射流的密度为1g/cm3,此时空气密度约为1.29kg/m3,因为空气密度与水密度之比约为1/1 000,因此相对于水炮射流质点的重力而言,其浮力非常微小,可以忽略。因此一般都只考虑空气阻力和重力,而不考虑浮力[2]。然而海洋环境中风往往较大,对水炮射流轨迹影响较大。因此本文在射流理论模型中对风力予以考虑,通过传感器得到风力Fw,假设v为质点的运动速度,θ为质点的运动方向与x轴的夹角,Fr为空气阻力,mg为质点所受的重力,Fw为风的阻力,φ为风力与x轴负向的夹角,φ为三维空间中风力与射流平面的夹角,可由风向传感器测量得到。如图1所示进行受力分析,其中i,j为质点运动方向的坐标系,i与v同向,j与v垂直。
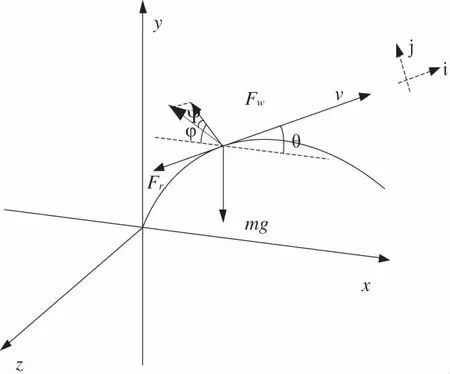
图1 水炮射流质点受力分析图
(1)
当时间间隔dt很小(趋于0时),di的指向趋于j的指向,单位矢量中可得di的大小为:di=|i|×dθ=dθ,由矢量微分原理可知:
(2)
将式(2)代入式(1)得:
(3)
将式(3)两边同乘m得到:
(4)
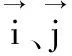
(5)
(6)
其中x、y分别为水炮射流轨迹质点的射高与射程。
1.2 空气阻力Fr的确定
模仿弹道系统在空中的运动,可以近似认为高压水炮射流质点在离开炮管后所受空气阻力与低速炮弹离开炮管受到的空气阻力相似,进而参考弹道系统的分析研究[3],根据质点运动和弹道学[4-5]知识可以确定水炮射流质点脱离炮口运动所受空气阻力大小可近似用式(7)表示:
(7)
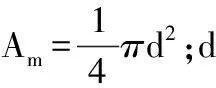
可以用水炮炮口的横截面积近似代替射流水柱的横截面积,方便近似计算。其中直径d可以直接测量或者通过水炮的结构参数手册查找得到。
1.3 风的阻力的确定
海洋环境中风速较大,风向复杂,对射流轨迹影响较大。尤其在水流后半段,由于动能减小[6],风力对水炮射流轨迹的影响显著,所以射流理论模型需考虑风力影响。由于空气阻力包含一部分风速,当风速较小时可以不予考虑;但是当风速大于一定值时必须考虑风的影响;风速与风向可以通过传感器测得。
风速风向传感器一般由风速、风向传感器(感应探头)、显示器、电缆组成,例如HL-FSXL型产品,DC 5~36 V的电源要求,可测量风速范围为0~70 m/s,风向范围:0°~360°;其输出为RS232或者RS485。可以通过串口将风速风向数据传送至PC端进行数据存储分析。
风压是指垂直于气流方向的平面所受到的风的压力[7]。根据伯努利方程得出风的动压可以表示为:Wp=0.5ρvw2,其中Wp为风压(g/m3),vw为风速(m/s),ρ为空气密度。
根据物理学压力与压强关系可以求得式(5)、式(6)中风的阻力大小为:
Fw=WpAm=0.5ρvw2Am
(8)
其中Am为式(7)中的射流水道截流面积。
2 方程计算求解
2.1 四阶龙格库塔求解方程
在1.1节中得到的四阶微分方程式(6),手工计算很难实现,然而现实中有许多算法可以借用。龙格库塔算法具有精度高、收敛、稳定(在一定条件下)、计算过程中可以改变步长、不需要计算高阶导数等优点,在工程中广泛应用于四阶微分方程的求解。因而本文采用龙格-库塔算法求解式(6)微分方程组。将式(6)转换整理得到式(9),将龙格库塔算法移植到水炮射流模型中得到四阶龙格-库塔计算公式。
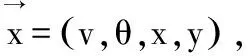
(9)
(10)
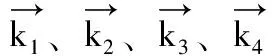
设定初始条件,通过编程计算即可求出水炮俯仰角度与射流射程的对应关系。
2.2 模型曲线图
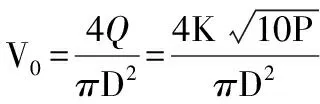
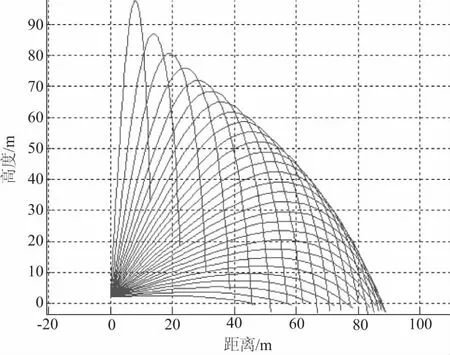
图2 角度与射流关系模型图
从中提取特定角度15°、30°、45°、60°的曲线得到如图3所示的特殊角度与射程关系图。
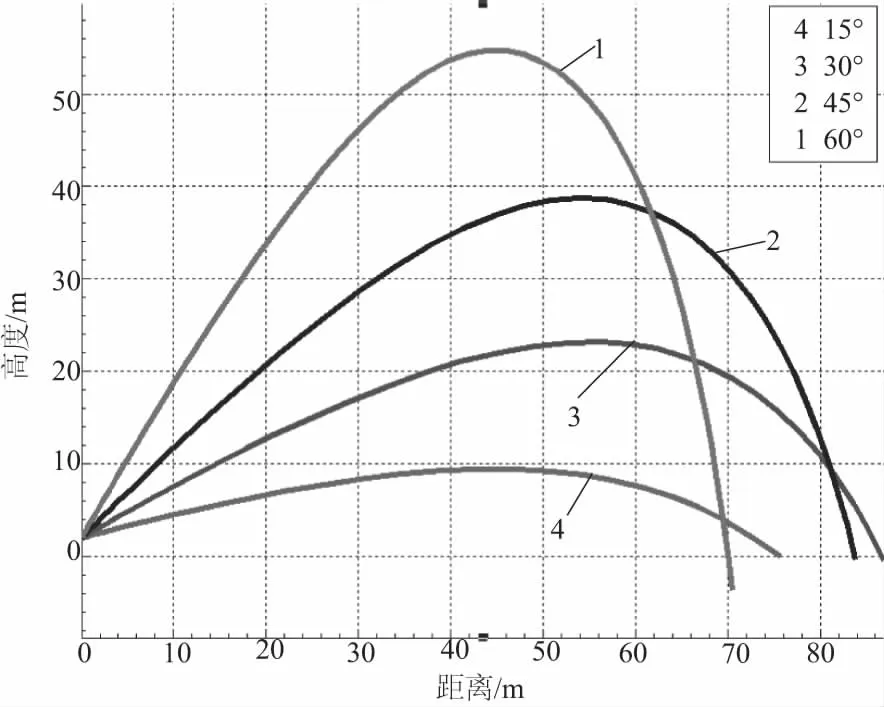
图3 特殊角度射流模型图
通过仿真图以及实验实际数据可以近似确定最大射程对应的角度为32°左右。此角度对确定可打击最远距离具有参考价值。由图1、图2可以看出,射流轨迹的走向、形状以及对应的射程与实际基本相同,说明仿真的正确性。为了进一步说明水炮射流理论模型可以实际应用,将进行多次实验,采集角度与射程数据,将同一角度的实际射程数据与理论数据加以比较,分析相应的误差。
2.3 实际射程与理论射程比较
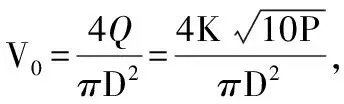
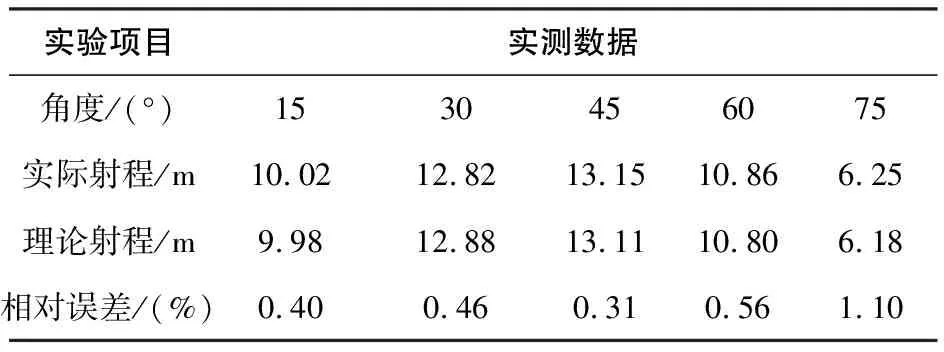
表1 实际射程与理论射程比较表
对表格内容加以分析可得,实际射程数据与模型得到的理论数据相近,且误差在一定的允许范围内[8],从而验证了上述建立的水炮射流理论模型的正确性及实用性,满足工程应用要求,可以实际应用于水炮俯仰角度的确定。实验中测得的风速大小为5.5~7.9m/s,当不考虑风速时,仿真结果得到的射程与实际射程有较大的误差。
将目标距离水炮的距离认定为水炮所需射程,通过射流模型得到对应角度信息,调整水炮的空间俯仰角度。为了提高系统的实时性,可以将角度θ细分为100份左右,将与之对应的射程数据关系存表,在程序中根据目标距离(所需射程),直接查表调用相应的水炮角度数据,提高程序运行速度,减小由于水炮的机械性能带来的相对于云台热像仪光电系统的略微滞后问题,提高系统的实时性。
3 射程主要影响因素
3.1 射流初速度
根据模型分析可知,水炮射流初速度V0对水炮的射程影响较大,间接影响水炮俯仰角度的确定;然而水炮射流初速度V0主要影响因素有流量、压力、水炮口径等,其关系可用以下公式表示:
(11)
其中:D是水炮炮口直径;Q为水炮射流流量(L/s)[9];P为炮口的工作压力(kPa);K为流量特性系数,注意根据实际情况不同,以及各参数的单位不同,K的值可能会有一定的差距,需视具体情况而定K值。
根据上述射流理论模型取俯仰角度θ为45°,初速度V0分别取15m/s、30 m/s、45 m/s、60m/s,得到射程曲线图(图4),从图4中可见射流初速度对射程影响较大,且具有相对明显的正比关系,速度越大,射程越远。
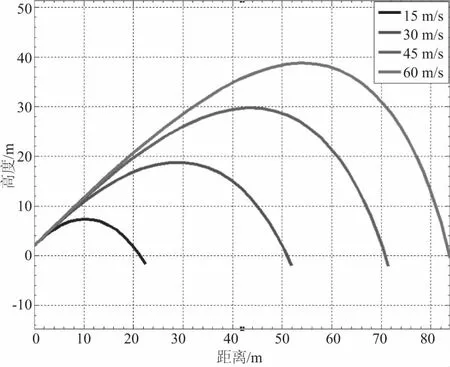
图4 初速度对射程的影响
3.2 工作压力及流量对射程的影响
当射流进入空气时,失去了水炮管壁约束,此时压力能完全转化为速度能[10]。由公式(11)可知,除了水炮的炮口直径D对射流初速度V0有影响,水流流量Q、炮口压力P对射流初速度V0也有一定影响,从而影响水炮射程。一般而言,当水炮工作压力增加时,流量Q也是增加的。水炮的流量与工作压力的关系可以表示为:
(12)
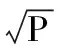
对于流量较小的水炮,通过增加水炮喷射流量,可以使射流以充实水柱喷射形式运动的距离显著增加,从而增加射程。对于额定流量较大的水炮,大量资料证明[11-12],简单地加大喷射流量Q或压力P,不能有效增加水炮的射程[9],通常情况反而会减小射程。具体而言,在一定压力范围内,射程随压力增大而增大;压力增大到一定程度时, 射程不再有明显增加;超出一定范围时,射程随压力的增大比例将会有所减小;当它们增加至一定值以后,射流会发生剥离破碎[9-10],此时射流横截面积会增大很多,由式(7)可知空气阻力Fr也会同时增加。此时由射流截面积变化导致的空气阻力变化变为射程的主要影响因素,从而使得水炮射程变小。因而提高大流量的高压水炮射程时需要综合考虑,在一定的范围内,合理、适当地调整水炮流量Q、炮口压力P等相关参数。
4 结语
本文综合考虑风力、空气阻力等影响因素建立射流理论模型,得出水炮俯仰角度与射程的关系,通过实验数据加以验证,可以看出数学模型相对精确,可以工程应用。分析了水炮射流初速度、压力、流量等因素对射程的影响,对实际调整水炮空间角度具有很大的参考价值。为使水炮射流准确,可以进一步考虑利用图像处理知识,辅助得到水炮射流落水点与目标的相对位置,根据位置差实时反馈闭环控制,及时辅助水炮控制系统微调水炮的空间角度,确保打击准确。
