仿壁虎机器人侧爬型地壁过渡步态Matlab仿真

王焕，杨佳欣，张昊,，尹铭泽，卢敏，倪进峰

(南京航空航天大学 a. 航天学院; b.机电学院，江苏 南京 210016)

0 引言

近年来，关于移动机器人的很多有价值的研究均集中在不规则地面、上下坡和阶梯等不同地面环境下的行走。各种粘附材料的成功制备使得机器人克服重力在垂直墙面上的行走成为一个新的研究热点[1]。南京航空航天大学仿生所的吉爱红、王周义等致力于壁虎脚掌粘附力的测试[2]、大壁虎在天花板上的运动行为研究[3-4]。大壁虎之所以能成为炙手可热的研究对象，一方面由于其超强的壁面行走能力，另一方面它能自如地从一个平面过渡到另一个平面，虽然目前很多研究机构已经研制出了各种可以在垂直壁面上行走的仿壁虎机器人[5]，但是从一个平面过渡到另一个平面的步态研究很少。2009年，首尔国立大学的Donghoon Son[6]提出了一套完整的算法研究了移动机器人从地面移动到墙面及在垂直面上的爬行步态，文章运用逆向运动学分析了机器人整个机身的雅克比矩阵，规划出了地壁过渡的步态。成均馆大学的Vo-Gia Loc等[7-8]人详细仿真了四足机器人在复杂地形上的行走，其中包括两相交平面之间的过渡，文章首先分析求解了足端工作空间，再通过筛选将其限制在行走面上，通过传感器判断障碍物距离与形态，调用步态规划算法来跨越障碍或者进行相交平面之间的过渡。张昊等[9]提出了一种侧向横爬型过渡步态，即当机器人身体轴线(头部与尾巴连线)与墙面平行时，机器人可以像螃蟹一样进行侧向横爬运动，以完全对称的步态过渡到墙面。西北工业大学曹飞祥等[10]设计并研究了一种具有柔性多杆机构腰部和尾巴的仿壁虎机器人结构，这种机器人可以跟真实壁虎一样双前腿和双后腿分别经过一次完整的步态过程跨上墙壁面。因此，研究出仿壁虎机器人从地面过渡到墙面的步态不仅可以运用于其他爬壁机器人、清洗机器人垂直面间过渡的步态，也可以应用于搜救机器人在地震现场、废弃建筑物里的行动，而且结合机器学习的知识，可以研究机器人自主规划垂直面间过渡的初始条件判断、爬行角度、步态选择。

1 仿壁虎机器人运动机构

如图1所示为南航仿生所研制的仿壁虎机器人，该机器人采用四足正向对称布置方式，腿部采用串联式旋转关节结构，每条腿具有6个自由度(3个主动驱动自由度，3个被动约束自由度)。1号电机负责抬、放腿动作；2号电机和3号电机负责完成脚掌在平面内的运动。球关节脚掌为自主恢复的3个被动约束自由度。从身体到腿依次往外为髋关节、膝关节和踝关节，其中髋关节由1号电机和2号电机组成，膝关节由3号电机组成，踝关节采用被动结构球铰链，帮助脚掌调整起姿态，其中，髋关节连接躯干与大腿，膝关节连接大腿与小腿，足端通过球关节与小腿相连。

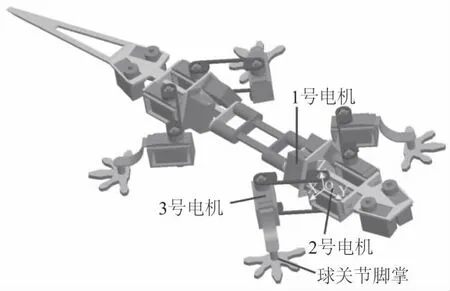
图1 南航仿壁虎机器人三维模型图

机器人结构简图如图2所示，腿部为串联连杆机构，任意一条腿包括l1、l2、l33个连杆以及J1、J2、J3、J44个关节。髋关节由轴线在空间中相互垂直的2个旋转关节J1，J2(抬腿、迈腿关节)组成，忽略电机安装导致的少量位移，2关节的中心在空间中重合；膝关节处为J3外摆关节；踝关节处为J4球关节。其中l1为大腿连杆，l2，l3为90°固接的平面连杆机构，组成机器人的小腿。

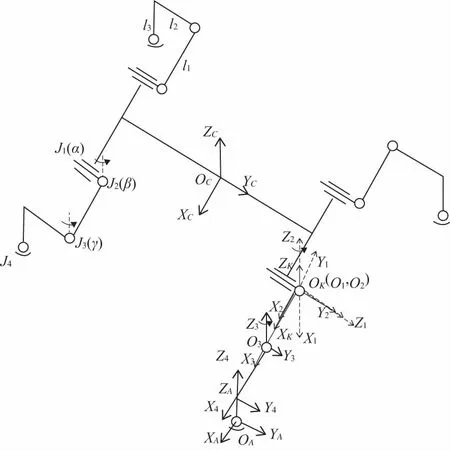
图2 仿壁虎机器人结构简图

建立如下坐标系：设OC为机器人的几何中心，Ki为髋关节处与机身固连的一点，Ai为足端中心，则OC处建立OC-XCYCZC为质心坐标系∑C，在Ki处建立腿基坐标系∑K(OK-XKYKZK)。在J1、J2、J3处依次建立O1-X1Y1Z1，O2-X2Y2Z2，O3-X3Y3Z3，分别为髋关节坐标系∑1，∑2，膝关节坐标系∑3，由于踝关节J4为被动自由度，故不建立坐标系，最后建立足端坐标系∑A(OA-XAYAZA)。需要说明的是，由于腿基坐标系∑K(OK-XKYKZK)与机身躯干固连，因此腿基坐标系与质心坐标系之间的位姿关系始终不变。

已知机器人的几何参数和各个关节的旋转变量，求末端部件相对于选定基准坐标系的位姿时首先建立连杆坐标系，取机器人右前腿为例，如图2所示。用D-H[11-14]法推导变换矩阵，代入机器人模型的数据，结合电机的运动范围以及机构的干涉情况，用变换矩阵求解得α、β和γ的转动范围分别为-55°～43°，-80°～60°，-38°～90°。其中机器人大腿长21 cm，小腿长18 cm。

右前腿的D-H参数见表1。

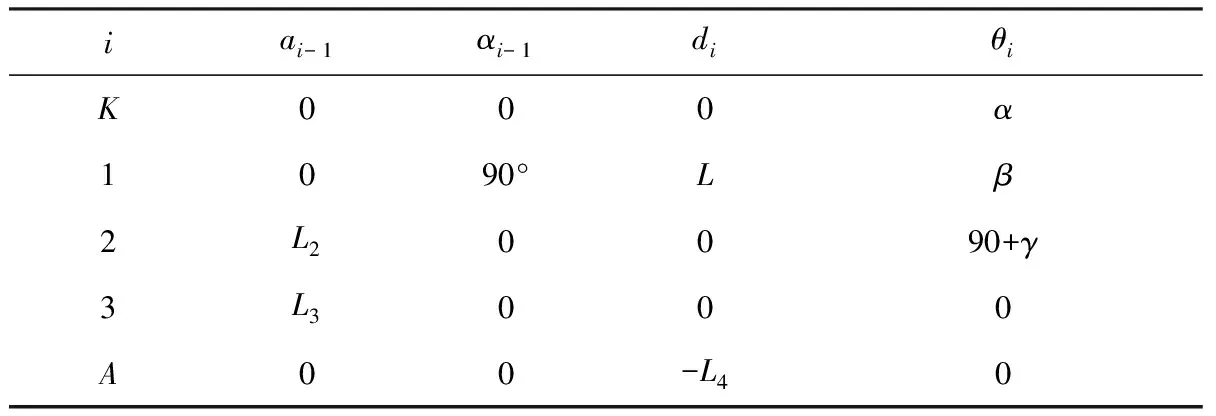
表1 右前腿D-H参数表

2 足端脚掌最优解求解

仿壁虎机器人采用对角步态[15-17]行走，身体前进的时候四肢分为两组前进，右前腿(right front leg)和左后腿(left hind leg)寻找落脚点的时候，左前腿(left front leg)和右后腿(right hind leg)保持支撑；左前腿和右后腿寻找落脚点的时候，右前腿和左后腿支撑。如图3所示，初始步态OC1中，由身体质心坐标正向推导得4个足端脚掌的落脚点RF1，RH1，LF1，LH1；步态OC1-OC2中，给身体重心坐标一个前进向量，通过新的身体重心位置推导得右前腿和左后腿的足端脚掌落脚点RF2，LH2，右前腿和左后腿为摆动相，左前腿和右后腿为支撑相，落脚点LF2和RH2同LF1和RH1一样；步态OC2-OC3中，右前腿和左后腿变为支撑相驱动身体前进，落脚点RF3和LH3同RF2和LH2一样，通过RF2和LH2运用逆向运动学反推得OC3中的关节旋转角度，左前腿和右后腿变为摆动相，落脚点为LF3，RH3。如此循环利用正向运动学和逆向运动学完成对角步态的行走。

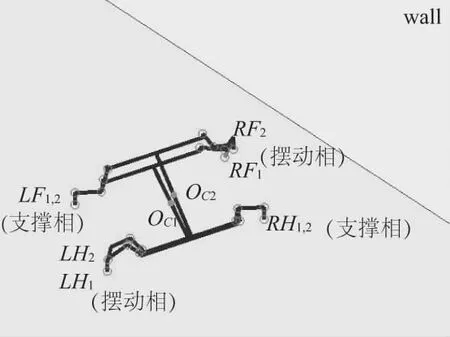
图3 仿壁虎机器人对角步态Matlab仿真

机器人足端运动空间[18-20]是指机器人足端参考点所可以达到点的集合，代表了机器人的活动范围，是衡量机器人工作能力的重要指标。机器人的工作空间可以分为两类，第一类是灵活工作空间，指机器人足端能够以任何方位到达的目标点集合；第二类是可达工作空间，指机器人足端能够以至少一个方位到达的目标点集合。本文所研究仿壁虎机器人足端脚掌的工作空间为可达工作空间，即机器人脚掌能够以至少一个方位到达的目标点集合，具体求解过程如下：

1) 求解机器人足端脚掌的运动学正解，并根据正解求出机器人足端脚掌在世界坐标系中的坐标值；

2) 在各个关节转动范围内，依次从大腿抬起角度、腿机构相对于身体的旋转角度和小腿相对于大腿的旋转角度以一定的步距角转动，得到多种关节变量组合；

3) 将各种关节变量组合代入变换矩阵，求出足端脚掌在各种情况下的坐标值。

以机器人身体中心为坐标原点，用机器人足端脚掌在该坐标系中的一系列坐标值点的集合表示机器人在世界坐标系中的运动范围。用D-H参数法推导从身体中心坐标系到足端脚掌的变换矩阵，最终计算结果如下：

在上式中，求解工作空间所用到的足端脚掌的坐标值为第四列，即足端脚掌在世界坐标系中的位置：

将上文求得的α、β和γ的转动范围分别为-55°～43°，-80°～60°，-38°～90°代入程序，按照上文描述的步骤，画出足端脚掌的运动空间，如图4所示。

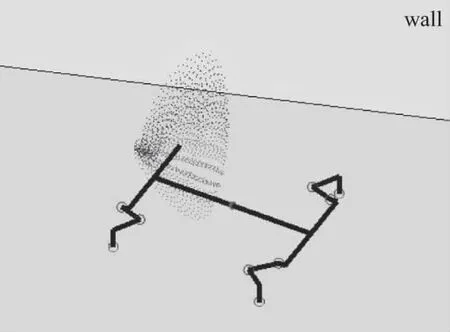
图4 右前腿足端脚掌的工作空间

机器人实际的过渡步态是一个不断调整身体和四肢的过程，这就需要根据前一步来筛选后一步的足端工作空间，从而筛选出最优过渡的关节变量范围。定义前一个步态的足端坐标值RF1[xi,yi,zi]，后一个步态的足端坐标值RF2[xi+1,yi+1,zi+1]，以右前腿地面爬行为例，过程如下：

① 首先画出右前足端脚掌完整工作区间；

② 求解工作区间与地面的交集，如图5(a)所示，蓝色部分为右前脚掌落脚点RF1的集合，黑色部分为落脚点RF2的集合，黑色和蓝色的交集部分既是步态OC1的解集，同时又是步态OC2驱动身体向前的解集(因本刊是黑白印刷，有需要详细了解的请与作者联系)。

③ 由于整体是斜向前的爬行，所以xi+1和yi+1均大于xi和yi；

④ 由于整体是斜上爬的过程，所以地面爬行和墙面过渡的过程中zi+1大于zi。

从位置OC1到OC2，按筛选规则逐步缩小工作空间范围，假设这个范围是等质量的，计算出这个最优区间的质量点，即认为这个质量点为最优落脚点，如图5(b)所示。

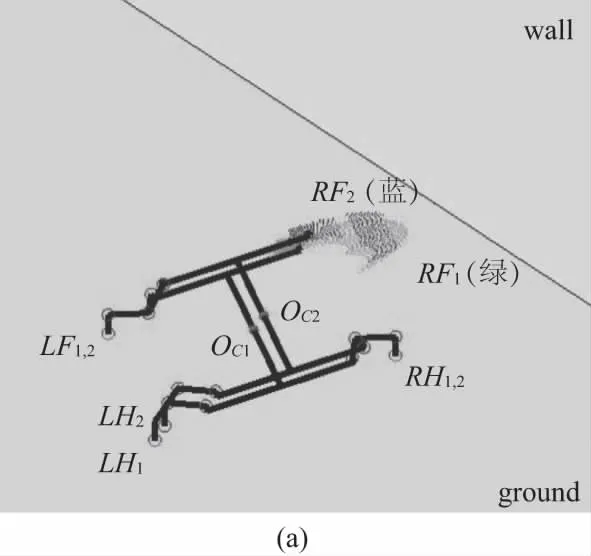
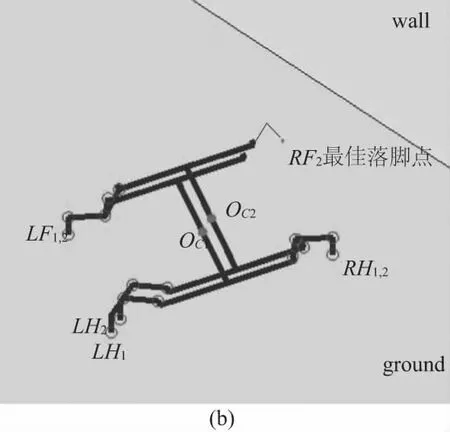
图5 筛选后的右前腿足端脚掌工作空间

3 仿壁虎机器人地壁过渡步态Matlab仿真

本文所研究的是机器人身体纵向截面和墙壁夹角从0°～90°的任意夹角时的过渡步态。因为仿壁虎机器人腰部是刚性构件，不能进行弯曲，即当身体纵向截面和墙壁面垂直时不能像生物壁虎一样，以直爬方式过渡。本节分别模拟当身体纵向截面和墙面呈10°角和60°角的过渡步态，且省略在地面行走和墙壁面行走的部分，着重规划过渡瞬间下四肢的迈步状态，并求解出可以进行侧爬过渡方式的夹角范围以及机器人身体中心距墙壁面的距离范围。当壁虎机器人质心进入这个距离范围时，采用本文所规划的步态方法从地面过渡到墙面。

仿壁虎机器人的初始位置如图6所示，身体中心坐标为OC1(x1,y1,h)，高度为h，机器人身体与y轴的夹角为θ；结束位置机器人的中心坐标为OC10(h,y10,z10)，身体与y轴的夹角为θ。首末中心点连线的空间直线方程为：

将空间直线轨迹划分为10个关键姿态。初始位置时，机器人身体绕自身坐标系y轴旋转角度为0°，即身体横截面与地面平行，在中心点OCn(n=2,3,…,10)位置时身体绕y轴旋转角度为10(n-1)度。结束位置时，机器人身体绕自身坐标系y轴旋转角度为90°，身体横截面平面与墙面平行。

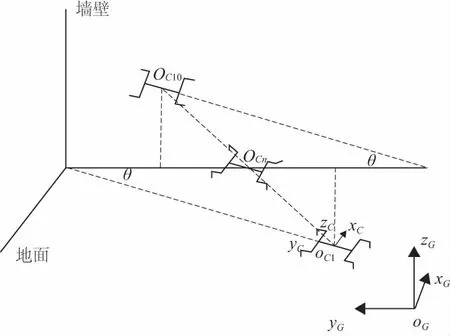
图6 机器人侧爬的中心轨迹规划

用这10个关键姿态在3ds MAX中初步拟定一个轨迹，拟合关键点画出一条样条曲线，在曲线上重新选择8个关键点，已知身体中心坐标，当θ=10°时，用上文的方法初步计算出身体坐标系相对于世界坐标系的旋转角度和4条腿各关节的旋转角度，如表2所示。假设机器人经过一个完整序列8步过渡到墙壁面，设置地面和墙壁面垂直相交的模型，地面和墙面长宽均为800 mm，身体中心相对于世界坐标系的位置矩阵为[Cx,Cy,Cz]；身体相对于自身坐标系的转动矩阵[δ1,δ2,δ3]，δ1、δ2、δ3分别为绕z轴、x轴和y轴的旋转角度；4条腿的关节变量矩阵[α,β,γ]，α、β、γ分别为大腿的抬起角度，腿机构相对于身体的旋转角度，小腿相对于大腿的旋转角度。

规划关节数据的过程如下：腿部的关节转动会随着身体的旋转而旋转，第一步为过渡之前的准备状态，身体相对于自身坐标系z轴旋转10°，身体纵向截面和墙面呈一定夹角；第二步右前腿跨上墙壁面时，身体绕自身坐标系y轴旋转5°进行微调，此时其余3条腿大腿会抬起一定角度，后面步态以此类推。但是规划的过程中各个角度不能超出前文中求出的转动范围。最后机器人跨上墙壁之后经过调整和初始在地面上的状态相同，且关于中间状态是对称的。

在Matlab中首先建立和理论分析中一致的地壁模型，地面和墙壁面相互垂直，设地面和墙壁面的长宽均为800 mm；然后根据机器人实际模型的大小建立杆机构模型；再分别建立世界坐标系，身体坐标系和腿基坐标系，并且写出各个坐标系之间的转换矩阵和足端脚掌相对于世界坐标系之间的转换矩阵，仿真结果如图7所示，wall代表墙面，ground代表地面，两个平面垂直相交，由仿真过程可以看出机器人关节可以利用前文所规划的数据进行一次完整的过渡步态。

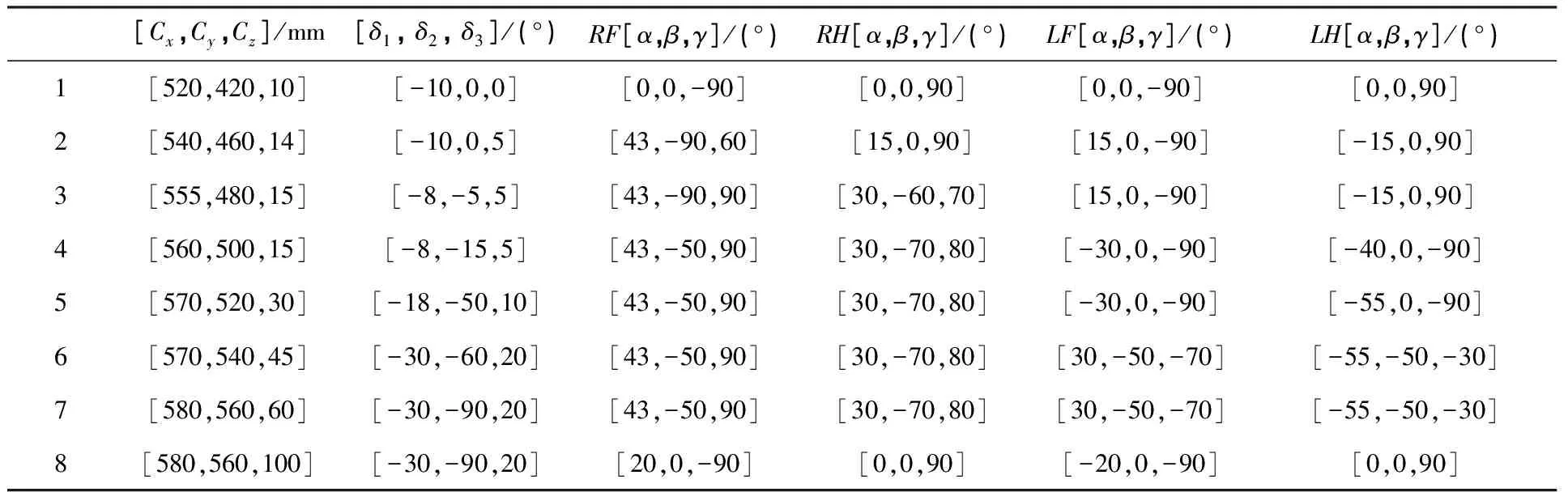
表2 机器人身体中心及各个腿关节旋转数据(10°)

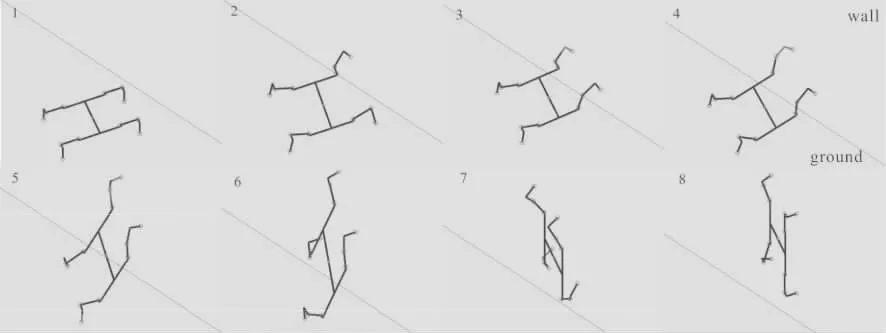
图7 仿壁虎机器人从地面过渡到墙面的步态仿真(10°夹角)

当身体纵向截面和墙壁面的夹角不断增大时就会出现一个临界角，目前计算得到临界角为60°。超过临界角时，机器人的前肢跨上墙壁后，由于刚性构件的腰部不能进行弯曲，后肢够不到墙壁，机器人就不能够以侧爬的方式爬上墙壁面，必须先调整身体纵向截面和墙壁面的夹角，调至临界角以内，再以侧爬方式过渡到墙壁面。表3所示为同样的方法计算得到的仿壁虎机器人各关节数据，同上，得到图8所示的仿真过程。值得注意的是，过渡过程中右后腿和左前腿的抬起顺序由落脚点与墙壁的距离决定，哪只足端脚掌到墙壁的距离先小于步长乘以身体纵向截面和墙壁夹角的余弦值，哪只腿就紧随右前腿跨上墙壁。后期的研究中可以在身体中心安装距离传感器，测量身体中心离墙壁的距离，再经过变换矩阵求出各足端脚掌离墙壁的距离，判断抬脚顺序。

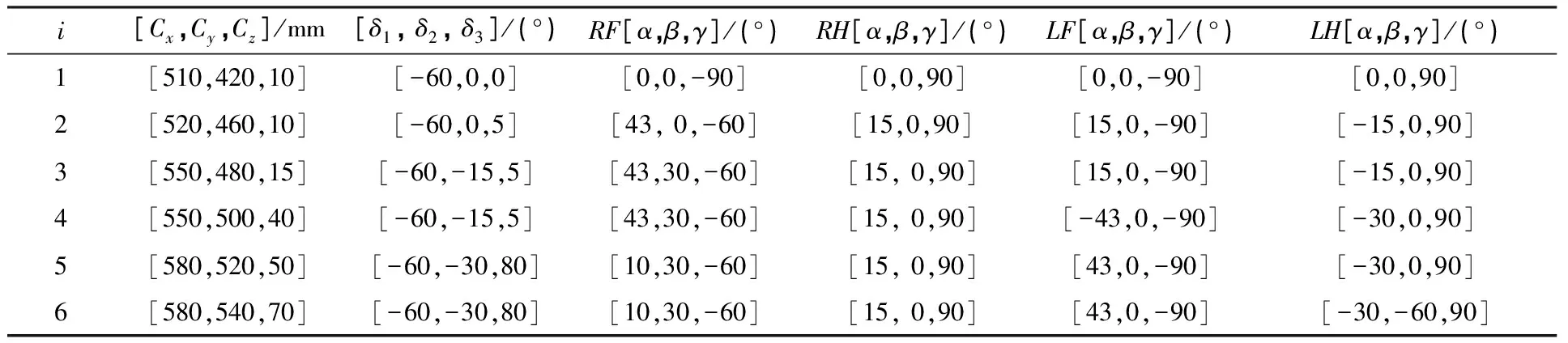
表3 机器人身体中心及各个腿关节旋转数据(60°)

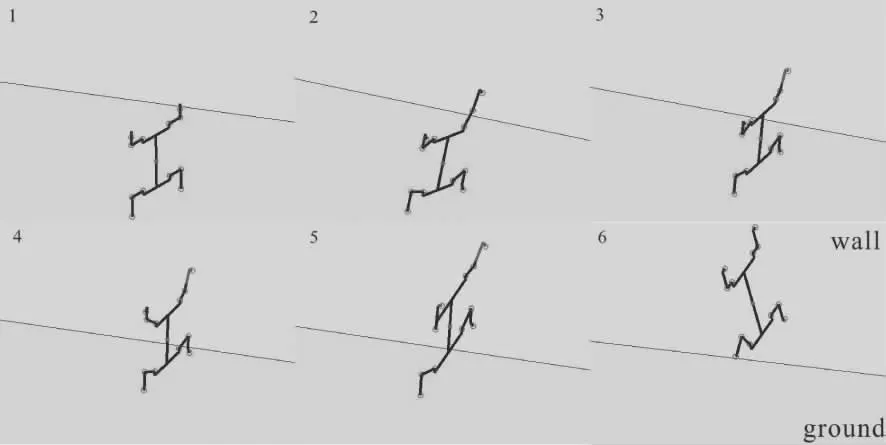
图8 仿壁虎机器人从地面过渡到墙面的步态仿真(60°夹角)

机器人实际爬行中关键步态中间的步态可以通过插值法计算得到。首先插值求出身体中心坐标，再通过变换矩阵求得各足端脚掌的坐标，用前文所述方法求解每一个步态中4个足端脚掌的落脚点，从而可以得到整个过渡过程中的步态序列和关节数据，对整个过渡过程实现仿真。

4 结语

本文通过Matlab软件规划并仿真了仿壁虎机器人的侧爬式地壁过渡步态。首先建立了仿壁虎机器人杆结构模型，详细计算了仿壁虎机器人足端脚掌在侧爬式地壁过渡过程中每一个步态中确定落脚点的过程，用正逆向运动学交替的方法确定了对角步态下每一步中从完整工作空间筛选到最优落脚点的过程，然后用插值法规划了过渡过程中机器人身体中心的轨迹。在轨迹上选取关键点，用Matlab计算得到关键步态的关节旋转数据。对整个过程进行了仿真分析，为仿壁虎机器人的过渡步态提供了数据支撑。