高阶变性椭圆齿轮副接触应力研究

刘炀，韩飞，张国花，王志伟

(合肥工业大学，安徽 合肥 230000)

0 引言

通常将节曲线为圆形的齿轮称为圆柱形齿轮。非圆齿轮就是节曲线为非圆形状的齿轮。圆柱齿轮极径随着极角变化是固定不变的，而非圆齿轮的极径随极角变化而变化[1]。

根据齿轮副传动比的计算公式可知，圆柱形齿轮的传动比是恒定的。而非圆齿轮由于其节曲线上各点距回转中心的距离各不相同，所以非圆齿轮传动的过程中，其传动比是变化的，当非圆齿轮节曲线上各点与回转中心之间的距离按照一定的函数关系变化时，其传动比也是按照一定的函数规律进行变化的[2]。在工程实际中，非圆齿轮多用于要求传动比呈一定规律变化的场合。

1 高阶变性椭圆齿轮节曲线方程

高阶变性椭圆齿轮机构是节曲线为高阶变性椭圆形状的齿轮机构，高阶变性椭圆是由普通椭圆通过变性和升阶变形得来的[3]。

高阶变性椭圆齿轮的节曲线极坐标方程为：

(1)

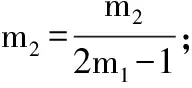
式中:n1为高阶变性椭圆齿轮中主动轮的阶数，m1为主动轮的变性系数，由设计高阶变性椭圆齿轮时所取参数确定。

假设高阶变性椭圆齿轮副的中心距为a，则从动轮的极坐标方程为[4]：

r2=a-r1

(2)

1.1 高阶变性椭圆齿轮的传动规律

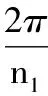
图1 主动轮极径随极角变化规律

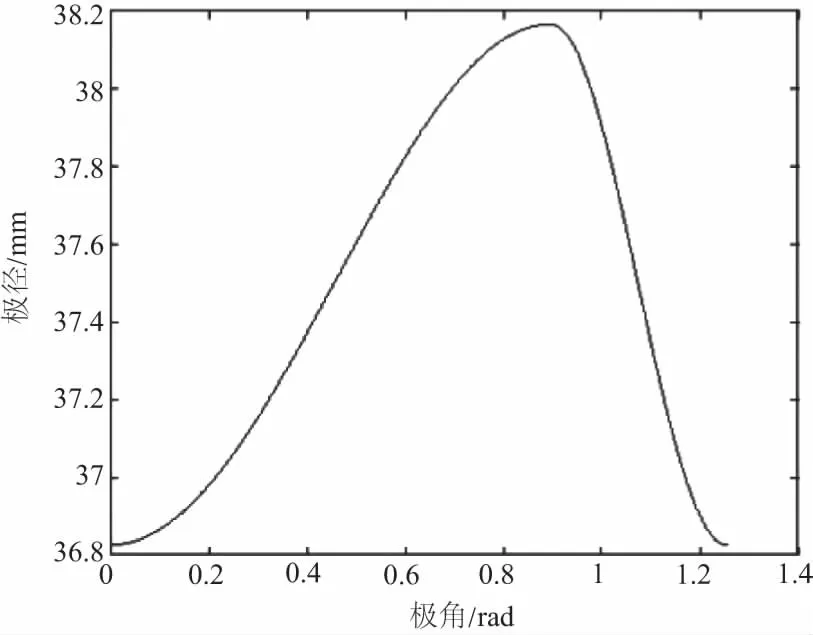
图2 从动轮极径随极角变化规律

根据传动比的计算公式可知，高阶变性椭圆齿轮副的传动比为：

(3)

根据齿轮副中主从动轮的极径随极角的变化曲线可以推得，由于主动轮极径随极角先减小后增大，从动轮的极径随极角先增大后减小，则由公式(3)可得，齿轮副传动比随极角增大，先减小后增大，则运用Matlab绘制传动比随极角的变化规律如图3所示。

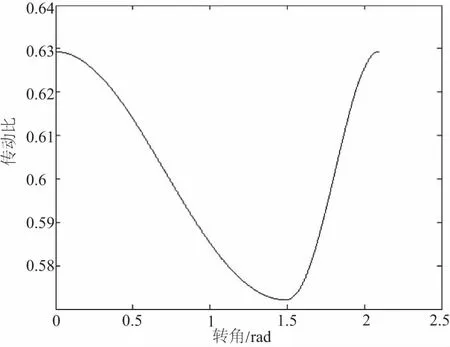
图3 齿轮副传动比变化曲线

假设主动轮以角速度ω1匀速转动，将r1看作是转角φ1的函数，则将ω2对φ1求导可得从动轮的角加速度为：

(4)

对公式(4)运用Matlab做出从动轮关于转角的变化曲线如图4所示。

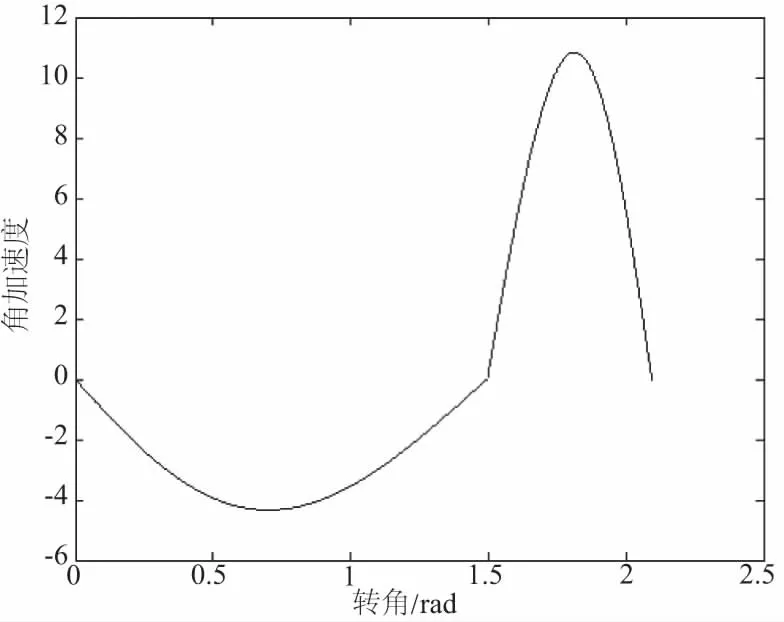
图4 齿轮副从动轮角加速度变化曲线

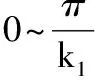
1.2 高阶变性椭圆齿轮机构力与力矩的传递

非圆齿轮受力分析如图5所示，根据非圆齿轮副接触力的计算公式可得，高阶变性椭圆齿轮副齿面上的接触力为：

(5)

式中：Mmp为齿轮副主动轮上动力的瞬时功率；Mdf为加在从动轮上负载的瞬时功率,做负功；α12为节点的压力角。

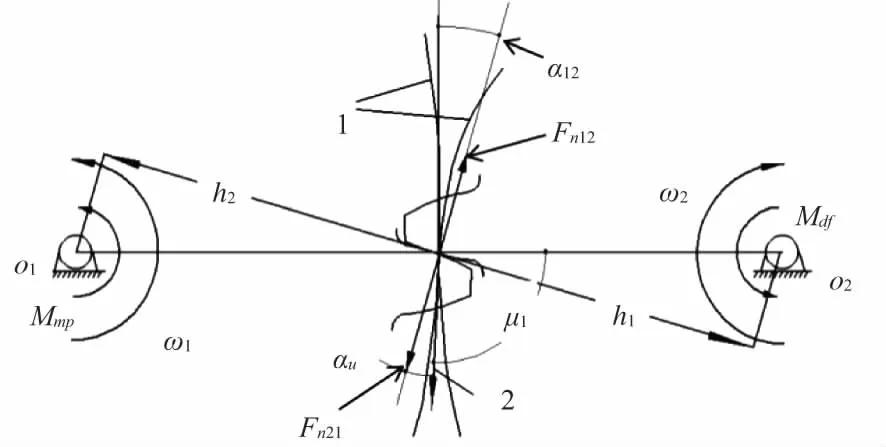
图5 非圆齿轮受力

由于主动轮角速度ω1为定值，则ε1为0，Jt1对φ1的导数为0，则：

(6)

1.3 高阶变性椭圆齿轮工作过程中接触力变化情况分析

由上节可知，当高阶变性椭圆齿轮副的主动轮以一定的角速度ω1转动时，Jt1对φ1的导数和ε1均为0。

齿轮副主动轮上的主动力矩Mmp为：

(7)

则将式(7)代入式(6)可得：

(8)

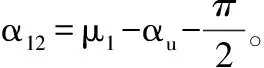
(9)

其中，r1和r2分别为非圆齿轮副在该瞬时主动轮与从动轮啮合点处的极径，再将ω2对极角θ进行求导，可得到从动轮的角加速度ε2：

(10)

根据公式(8)进行分析可得，齿轮齿面上的接触力Fn12与参数Mdf，Jt2,ε2,r2和cosα12有关，则可以根据公式来分析齿面方向接触力Fn12的变化规律，且根据高阶节曲线的基本知识可以推得。若主动轮为n1阶，则在主动轮旋转一周时，节曲线变化n1个周期，周期与周期期间的各个参数均相同，则齿面的法向接触力Fn12在主动轮旋转的一个周期中将出现n1个峰值，则初步推断主动轮的阶数n1与周期内齿面法向接触力Fn12的峰值数相同。由齿轮齿面法向接触力的公式可知，其中参数与从动轮阶数n2无关，则初步推断法向接触力与从动轮阶数n2无关。下面分情况进行齿面方向接触力Fn12的变化规律分析及验证。

当从动轮上的阻力矩较小，导致当角加速度ε2为负时Mdf+Jt2ε2<0时，齿面方向接触力Fn12将<0，此时说明主动轮与从动轮脱开，法向接触力为0。

当从动轮上所加的阻力矩Mdf较大，导致Jt2ε2小到可以忽略时，Mdf+Jt2ε2与Mdf近似相等为定值，则齿面方向接触力Fn12的变化规律由公式的分母r2cosα12确定。此时Fn12的变化规律运用Matlab作图而得。

选用参数Mdf=600、Jt2=20对三阶齿轮运用Matlab绘图，结果如图6所示。

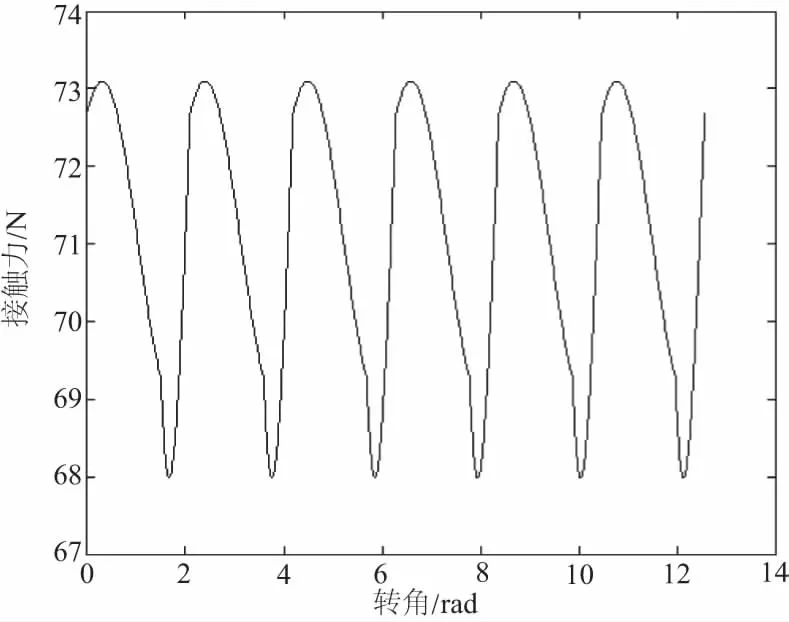
图6 n1=3，n2=3时,Mdf较大时Fn12的变化规律理论曲线

再以同样类型的条件将齿轮副导入到Adams中进行接触力分析可得到曲线如图7所示。

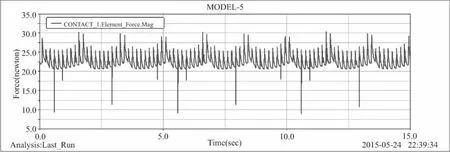
图7 n1=3，n2=3时,Mdf较大时Fn12的变化规律实际曲线

将理论图像与运用Adams进行分析所得的实际图像进行比较，由于在理论图像绘制时并未考虑重合度的问题，则导致实际图像与理论图像有一定的误差，但是两者图像近似，初步证明上述Fn12的变化规律分析正确。

当节曲线的极径变化比较平缓时(即传动比最大值与最小值之比接近于1时)，cosα12值的变化范围相对较小，在计算中可以忽略，则齿面接触力的变化主要由角加速度ε2和从动轮的极径r2决定。

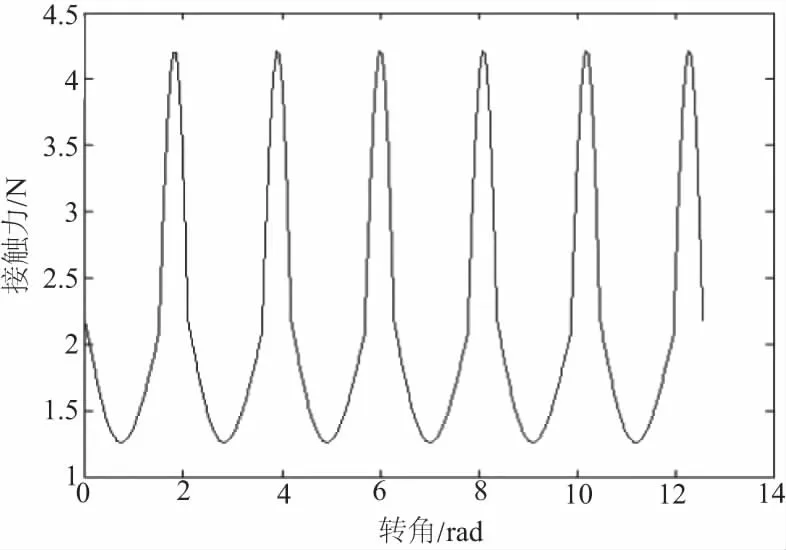
图8 n1=3、n2=3时，Fn12的变化规律理论曲线

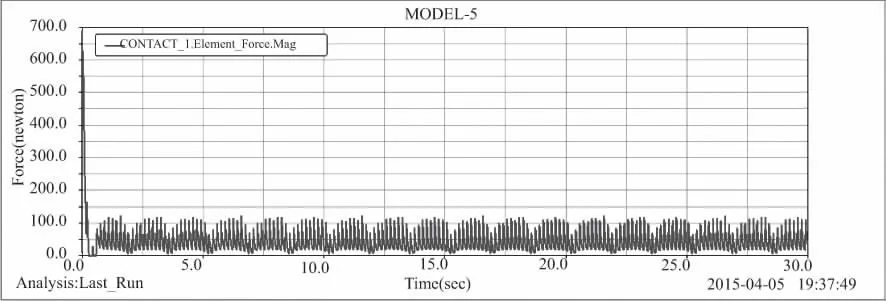
图9 n1=3、n2=3时，Fn12的变化规律实际曲线

与上述分析相同，由于重合度的问题导致Fn12的最大值位置有所不同，但是其变化规律相同，初步证明上述Fn12的变化规律分析正确。

但是当节曲线的极径变化剧烈(即传动比最大值与最小值之比较大时)，cosα12值的变化范围相对较大，此时Fn12的变化规律可根据绘图观察而得，而最大值出现的位置能够通过求得使Fn12表达式为0的点而得到。

1.4 高阶变性椭圆齿轮机构接触应力计算公式推导

由上节已知，通过非圆齿轮副的实际运行的状况可以由公式求得齿轮副轮齿接触面上的法向力，在求得齿轮副齿面上的法向力之后，通过赫兹理论，可以求得齿面上的接触应力，受力分析及计算示意如图10所示。

由赫兹理论的公式可知，两接触面的接触应力为[5]：

(11)

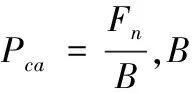
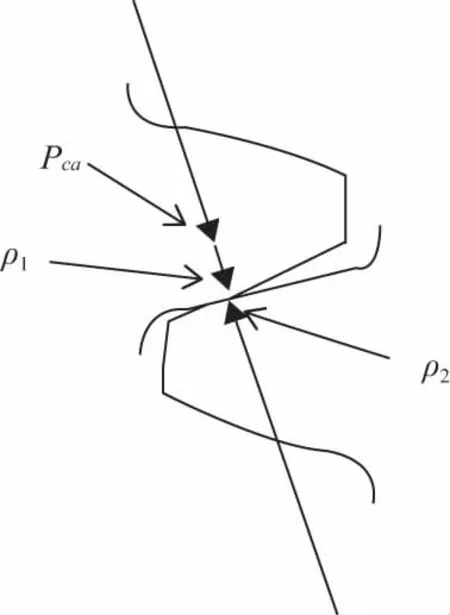
图10 赫兹理论计算公式示意图

在高阶变性椭圆齿轮中，虽然非圆齿轮在节曲线上各处齿形互不相同，但是运用圆柱齿轮的齿形来近似计算相互接触处的综合曲率半径，则由公式有：

(12)

其中，i为传动比，α为齿形压力角，一般为20°。d1为小齿轮的分度圆半径，对于非圆齿轮副来说，d1为啮合点处的曲率半径的2倍。

2 高阶变性椭圆齿轮接触应力分析

上节通过Matlab进行了轮齿齿面接触力的变化曲线的模拟，得出了非圆齿轮副运转过程中齿轮齿面的接触力的变化规律，下面运用Ansys进行静接触应力分析证明运用齿轮的赫兹理论公式进行非圆齿轮齿面接触应力的正确性。

由Jt2的定义可知，Jt2为与从动轮相联结的构件转化到从动轮上的转动惯量，所以为了简化计算过程，提高Ansys接触应力计算的效率，将分析的模型进行简化，去除掉与主动轮和从动轮相联结的构件，仅对2个齿轮的装配体进行应力分析，则Jt2=0，将式(7)化简可得：

由于加在从动轮上的阻力矩为定值，在每一个瞬时，齿轮副的传动比为一个定值，则由上式可得Mmp也为一个定值。由于需要对齿轮副进行静接触应力分析，所以直接在主动轮上给定一个主动力矩进行接触应力分析，虽然此时阻力矩不为定值，但是对每个啮合的轮齿来说，给定主动力矩能够通过公式算出齿面上的法向接触力，对于验证齿轮的赫兹理论计算公式是可行的。

2.1 高阶变性椭圆齿轮静接触应力分析过程

运用Workbench中的静力结构模块(static structural)，将齿轮三维模型导入到Ansys中，定义其为结构钢(structural steel)，再在齿轮副上加上No separate接触类型，以一对啮合齿面为目标面和接触面定义接触。再确定边界条件：约束方面，运用远端约束(remote displacement)约束掉主动轮的x，y，z方向的移动自由度及x，y方向的转动自由度，并保持主动轮绕z轴转动的自由度；再运用固定约束(fixed)将从动轮固定。动力方面，在主动轮上加上与主动轮运转方向相同的动力矩Mmp。观察冯米塞斯应力云图(von-mises stress)，接触面附近应力的最大值就是所要求得的接触应力[6]。

2.2 高阶变性椭圆齿轮静接触应力分析结果

图11 主动轮为三阶，从动轮为五阶的高阶变性椭圆齿轮的齿面接触应力云图

选择载荷系数K=1.3，E1和E2为200 GPa，μ1和μ2为0.3，将上述参数带入公式计算得到齿面的接触应力为756.988 MPa。再从应力云图中读数得出接触面附近的最大应力值为733.46 MPa。计算可得公式的误差为3.1%，在误差范围之内，所以初步证实了高阶变性椭圆齿轮齿面接触应力计算公式的可行性。

3 结语

本文对高阶变性椭圆齿轮的接触应力作了相应的研究，所做研究结果如下：

1) 得出了高阶变性椭圆齿轮副运转过程中齿面接触力的变化规律。

2)推导出了高阶变性椭圆齿轮副接触应力计算的可用公式。

3)运用Ansys初步验证了接触应力计算公式的可行性。