基于改进遗传算法的浮法玻璃优化切割

王聪聪，杨明顺，原 欣，高新勤

WANG Congcong,YANG Mingshun,YUAN Xin,GAO Xinqin

西安理工大学 机械与精密仪器工程学院，西安 710048

School of Mechanical and Precision Instrument Engineering,Xi’an University of Technology,Xi’an 710048,China

1 引言

浮法玻璃是平板玻璃的一种，具有表面平整光滑、透视性佳、厚度均匀等优点，广泛应用于制镜玻璃、汽车挡风玻璃、建筑门窗等多个方面[1]。和普通平板玻璃不同，浮法玻璃生产过程中的许多因素都会导致玻璃表面产生各种缺陷，而以目前的生产水平，浮法玻璃厂家很难杜绝缺陷的出现[2]，这些缺陷的种类、数量和大小会不同程度地影响玻璃质量，进而影响玻璃价格。因此，在浮法玻璃切割过程中，仅关注提高玻璃原板利用率的传统切割方法对浮法玻璃不再适用，必须根据浮法玻璃的生产特性，提出新的优化切割方案。

玻璃切割问题是一个典型的组合优化问题，类似的问题还有二维下料问题、矩形件排样问题、二维装箱问题等。近年来，学者们对该类问题进行了大量研究。文献[3]针对玻璃优化切割问题，以玻璃原板利用率最大为优化目标，提出了一种启发式优化排样算法，并通过实例对该算法进行了验证；文献[4]通过对玻璃切割问题的研究，以玻璃原板利用率最大为优化目标，提出了一种融合量子粒子群优化和蚁群优化的混合算法，并通过实验对该算法进行了验证；文献[5]针对有约束的两阶段二维切割问题，以板材利用率最大为优化目标，提出了一种并行算法，并以实例对该算法进行了验证；文献[6]针对矩形件二维下料问题，以板材利用率最大为优化目标，提出了一种单毛坯条带四块排样方法，并通过实验对该方法进行了验证；文献[7]针对多规格的两阶段二维一刀切下料问题，以板材利用率最大为优化目标，提出了一种列生成启发式算法，并以实例对该算法进行了验证；文献[8]针对一刀切矩形件排样问题，以板材利用率最大为优化目标，提出了一种将启发式递归与免疫克隆算法相结合的混合优化算法，并以两个实例对该算法进行了验证；文献[9]针对二维矩形件优化排样问题，以板材利用率最大为优化目标，提出了一种确定性启发式最佳匹配算法，并以两个实例对该算法进行了验证；文献[10]针对二维装箱问题，以填充率最大为优化目标，提出了一种混合进化算法，并通过实例对该算法进行了验证；文献[11]针对离线定向和不定向二维装箱问题，以填充率最大为优化目标，提出了一种超启发式算法，并通过实验对该算法进行了验证。

图1 浮法玻璃优化切割过程图示

上述算法都不同程度达到了减少材料浪费，提高原板利用率（填充率）的目的，但仅考虑提高玻璃原板利用率，并不能完全满足浮法玻璃优化切割的基本要求。浮法玻璃的价格是由切割获得的玻璃成品的面积和玻璃质量共同决定的，因此，即使玻璃原板利用率最大，也并不能保证玻璃成品总价格最高。

迄今为止，仅有少数学者在解决以上组合优化问题时，将缺陷对成品质量的影响考虑在内。文献[12]针对考虑质量要求的一维下料问题，提出了一种二阶段序列启发式算法，并以实例对该算法进行了验证；文献[13]针对考虑缺陷的二维切割问题，以切割获得的矩形块的价值最大为优化目标，提出了一种基于动态规划的启发式算法，并通过实例验证了算法的有效性；文献[14]针对纺织工业中考虑缺陷的布料切割问题，以总利润最大为优化目标提出了一种改进模拟退火算法，并通过实例证明了算法的有效性；文献[15]针对考虑缺陷的玻璃优化切割问题，以最小化切割获得的废品数量为优化目标，提出了一种基于动态规划的算法，并通过实例证明了算法的有效性。

本文在上述研究的基础上，结合浮法玻璃的生产实际，考虑相应的缺陷分级和玻璃分级标准，同时考虑提高玻璃成品质量和玻璃原板利用率，以玻璃成品总价格最大为优化目标建立数学模型，提出了一种符合浮法玻璃切割问题特性的遗传算法。

2 浮法玻璃优化切割问题简介

浮法玻璃的切割过程主要包括：缺陷检测、生成切割方案、纵向切割和横向切割4个步骤，如图1所示。在实际生产过程中，玻璃带被输送辊道缓慢匀速向前输送，在玻璃带运行过程中，首先，通过缺陷检测装置，获得玻璃带上各缺陷的位置、种类和大小等信息；其次，在已知玻璃缺陷信息的基础上，根据切割订单要求，在某一固定长度的玻璃带上生成有效的切割方案；最后，按照确定的切割方案实施纵向切割和横向切割，获得玻璃成品。

与普通平板玻璃切割相比，浮法玻璃优化切割的特性主要体现在以下三方面：

（1）浮法玻璃的切割工艺要求。纵切必须切整个板宽，中间不能抬刀，横切可以改变玻璃规格。据此可知，在规划切割方案时，只有长度相等的玻璃原片才能排放在玻璃原板的同一列。以表1中的切割订单为例：订单编号为1的玻璃原片可以和自身或编号为2的玻璃原片规划在同一列。

表1 切割订单

（2）浮法玻璃原片质量等级的判定。按照浮法玻璃国家标准或企业自行制定的标准，可将切割获得的玻璃成品划分为若干个质量等级，不同等级的玻璃允许含有的缺陷种类、数量和等级不同，玻璃质量等级越高，其每平方米价格越高，因此应尽可能切出质量等级较高的玻璃成品。

（3）玻璃原片的质量等级与其排放位置息息相关。如图2所示，假设排放在第1列第1个位置和第2个位置的订单编号分别为i和j(i≠j)，若交换这两块玻璃的排放位置，并不会改变玻璃原板的利用率，但由于玻璃原片的位置变动，其上包含的缺陷信息也随之改变。因此，当某块玻璃原片的位置发生变动，其质量等级需要根据新的缺陷信息进行重新判定。

图2 排放位置对玻璃原片质量的影响

3 数学模型

浮法玻璃优化切割问题是指：在一块已知长度、宽度以及缺陷信息的浮法玻璃板面上，根据订单要求切割一定规格的玻璃原片时，应优先规划质量较好的玻璃原片，并保证玻璃原板的利用率较大，以使得切割所得玻璃成品的销售总价最高。

该问题中各变量及其符号表示如下：

Length为玻璃原板的长度；Width为玻璃原板的宽度；n为玻璃原板上的缺陷点总数；D为缺陷集，其中即每个缺陷点均含有3个基本属性：缺陷位置pi，缺陷种类ti，缺陷大小si，其中pi=(xi,yi)，xi、yi分别为缺陷点中心到切割原点的横向和纵向距离，ti∈{气泡，夹杂，光畸变，锡灰，玻筋，线道，其他}。

m为切割订单包含的订单规格总数；CO表示切割订单，其中Oj=(lj,wj)，lj和wj分别表示切割订单中各订单规格对应的长度和宽度，l和w分别表示切割订单中所有订单规格对应的长度和宽度的集合，

DC为缺陷分级参数，用于判定缺陷的等级，DC=根据缺陷分级参数可将缺陷划分为H+1个等级，等级为H+1的缺陷也称为“不允许缺陷”。

QC为玻璃分级参数，用于判定玻璃原片的质量等级，其中O≤M1≤M2≤…≤MT，且矩阵Mt互不相等（“≤”表示前一个矩阵的所有元素均不超过后一个矩阵对应位置的元素）。Mt表示一个N×(H+1)的矩阵，O表示一个和矩阵Mt同型的零矩阵，N为玻璃原板上包含的缺陷种类数，矩阵Mt中第i行第j列的元素Mt(i,j)表示等级为t的玻璃每平方米允许含有种类为i等级为j的缺陷的数量，根据玻璃分级参数可将玻璃划分为T+1个质量等级，等级为T+1的玻璃也称为“废品级玻璃”。

SP为玻璃单位面积价格的集合，SP={St|t=1,其中St表示等级为t的玻璃每平方米价格为St。

xc,r为决策变量，其值等于排放在玻璃原板第c列的第r块玻璃原片的订单规格编号；colMax为玻璃原板上排放玻璃原片的最大列数；glaNumMax为每列最多可以排放的玻璃原片块数；colReal为玻璃原板上实际排放的玻璃原片的列数；glaNum(c)为第c列实际排放的玻璃原片的块数；集合cset为列数集合cset={1,2,…,colMax}；rset为块数集合，rset={1,2,…,glaNum(c)}；lrnd等于集合l中的任意一个值，即glassArr表示一个可行的切割方案；g(c,r)表示该切割方案中排放在玻璃原板第c列的第r块玻璃原片的信息集：

其中，xst(xc,r)和yst(xc,r)分别为该玻璃原片左下角距离切割原点的横向和纵向距离；lr(xc,r)和wr(xc,r)分别表示该玻璃原片的长度和宽度；Dr(xc,r)为该玻璃原片上包含的缺陷集，Dr(xc,r)∈D,nr为该玻璃原片上的缺陷总数，dpk、dtk、dsk分别表示该玻璃原片上各缺陷的位置、种类和大小，为该玻璃原片对应的缺陷计数矩阵，用来存储该玻璃原片实际每平方米包含的不同种类、不同等级缺陷的数量；glag(xc,r)为该玻璃原片的质量等级；pr(xc,r)为该块玻璃原片每平方米的价格。图3为一个可行切割方案示例。

该问题的目标函数及约束条件如下：

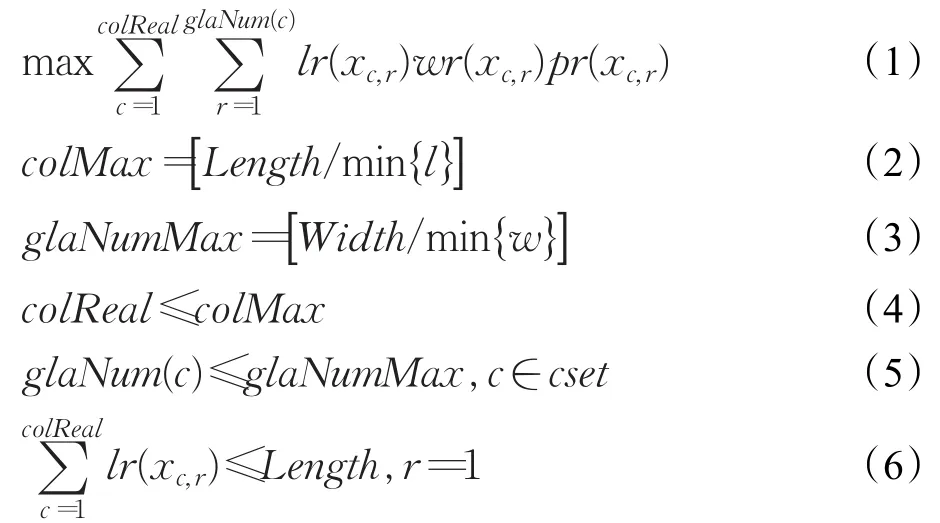
图3 可行切割方案示例

式（1）为目标函数的计算公式，其值为玻璃成品的总价格；式（2）、（3）为玻璃原板最多可以排放玻璃原片的列数colMax，及每列最多可以排放的玻璃原片的块数glaNumMax的计算公式；式（4）、（5）表示玻璃原板实际排放的玻璃原片的列数不超过colMax，每列实际排放的玻璃原片的块数不超过glaNumMax；式（6）、（7）分别为玻璃原板的长度约束和宽度约束，表示排放的所有玻璃原片均不能超过玻璃原板的边界；式（8）为排放在同一列的玻璃原片的等长约束，即排放在玻璃原板同一列的玻璃原片的长必须相等；式（9）为决策变量的取值范围，表示排放的玻璃原片的规格必须来自切割订单；式（10）、（11）为该玻璃原片上缺陷的位置约束，表示同时满足式（10）、（11）约束的缺陷点在该玻璃原片上；式（12）为缺陷等级的判定公式；式（13）为玻璃质量等级的判定公式，其含义为已知某块玻璃的缺陷计数矩阵CM，玻璃分级参数QC，首先判断CM≤M1是否成立（CM的所有元素均不超过玻璃分级参数矩阵M1对应位置的元素），若成立，则该玻璃等级为1，否则降级，继续判断CM≤M2是否成立，若成立，则该玻璃的等级为2，否则降级，继续判断，以此类推，若直至CM≤MT仍不成立，则该玻璃等级为T+1（即废品级）；式（14）为玻璃原片单位面积价格的判定公式，用于根据玻璃原片的质量等级进一步判定其每平方米的价格。

4 算法设计

浮法玻璃优化切割属于NP难类组合优化问题，随着订单规格的增加及缺陷信息的多样化，寻优过程将变得十分复杂，此时很难在有限时间内遍历所有解空间，从中找出最优解，因此精确求解算法不再适用。遗传算法是基于进化理论原理发展起来的一种高效的随机搜索算法，在解决组合优化问题时具有较好的性能。本文根据浮法玻璃优化切割问题的特点，提出了一种基于玻璃原片排放位置编码的遗传算法。以下对该算法的基本步骤进行说明。

4.1 编码

根据浮法玻璃切割“纵切必须切整个板宽”的要求（即排在同一列的订单规格的长度必须相等），以及玻璃原片排放位置对其质量等级的影响，提出了一种基于玻璃原片排放位置的序列编码方式。每条染色体含有gn=colMax×glaNumMax个基因，每个基因gi的取值为切割订单中某一个订单规格的编号，即区间 [glaNumMax×(k-1)+1,k×glaNumMax]上的基因值对应的玻璃规格的长度相等，

以表1中的订单规格为例，假设玻璃原板的长Length为12200，宽Width为4000，根据式（2）、（3）可知该玻璃原板最多可以排放6列，每列最多可以排放2块玻璃原片，染色体基因数gn=6×2=12。经过编码得到一个可能的染色体如图4所示，该染色体表示玻璃原板上每个位置拟排放的订单规格。如：第一个基因位上的元素7表示排放在玻璃原板第一列的第一块玻璃原片的订单规格编号为7；而编号为7和编号为6的订单规格的长度相等，可以排在同一列。

图4 染色体编码示例

4.2 解码

为得到具体规划方案，需要对染色体进行解码。根据玻璃原板的宽度约束和长度约束从左向右对染色体依次进行解码，获得每列实际允许排放的玻璃规格。图4所示染色体的解码结果为glassArr={(7,6),(5),(1,2),(4,3),(2,1)}，其含义为：玻璃原板第一列实际排放的订单规格编号依次为7和6，第二列排放的订单规格编号为5，以此类推。

4.3 种群初始化

为保证初始种群的多样性，采用一种启发式搜索算法获得符合浮法玻璃切割要求的初始种群。一个可行初始解的生成过程如下：

步骤1输入玻璃原板上可排放玻璃原片的最大列数colMax，每列可排放的玻璃原片的最大块数glaNumMax。

步骤2令c=1,r=2。

步骤3从切割订单中随机选择一个订单规格编号firstp，排放在第c列的第1个位置，即染色体的第glaNumMax×(c-1)+1个位置。

步骤4在切割订单中寻找和firstp等长的所有玻璃规格的编号，存放在集合eql中。

步骤5在等长订单规格集合eql中随机选择一个订单规格编号，排放在第c列第r个位置，即染色体的第glaNumMax×(c-1)+r个位置。

步骤6判断r=glaNumMax是否成立，若成立，继续进行步骤7，否则令r=r+1，转步骤5。

步骤7判断c=colMax是否成立，若成立，结束程序，否则，令r=2,c=c+1，转步骤3。

将以上过程循环N(p)次，即可获得该问题的初始种群。

4.4 计算适应度函数值

采用该问题的目标函数值作为该算法的适应度函数值，第i个染色体的适应度函数值的计算公式为：

某块玻璃原片的价格是由其面积lr×wr及其单位面积的价格pr共同决定的，当订单规格已知时，该玻璃原片的面积是确定的，但该玻璃原片单位面积的价格需要由其包含的缺陷信息判定。

以下给出根据某块玻璃原片上包含的缺陷信息，判定其质量等级，进而判定其单位面积价格的步骤：

步骤1输入缺陷分级参数DC,玻璃分级参数QC,玻璃单位面积价格的集合SP,玻璃原片上包含的缺陷集合Dr。

步骤2根据缺陷分级参数DC判定该玻璃原片上各缺陷的等级，见式（12），整理缺陷的种类和等级信息，获得该玻璃原片的缺陷计数矩阵CM。

步骤3根据缺陷计数矩阵CM判定该玻璃原片等级，见式（13）。

步骤4根据玻璃原片等级判定其每平方米价格，见式（14）。

根据以上过程，依次判断glassArr中每块玻璃原片的单位面积价格，再根据式（15）计算该染色体对应的适应度函数值。

4.5 选择算子

采用随机按比例的方式选择个体进入交配库，使得适应度函数值较大的个体被选择概率较大。

步骤1将所有个体的适应度函数值按照升序排列，得到集合Fsort。

步骤3将步骤2循环N(p)次，直至选满N(p)个个体为止。

4.6 交叉算子

为保证交叉后染色体的可行性，本文针对浮法玻璃切割问题的特点，提出了一种两点交叉法。

步骤1从选择操作产生的交配库中随机选取两个染色体F1、F2，作为交叉操作的父代。

步骤2随机产生两个交叉点P1、P2，为保证两个父代经过交叉后不破坏染色体的可行性，P1,P2∈{k×glaNumMax}，其中k=1,2,…,colMax-1，且P1≠P2。

步骤3将父代染色体F1中第[1,P1]、[P2+1,gn]之间的基因复制到子代染色体O1的对应位置，其中gn为染色体包含的基因总数。

步骤4将父代染色体F2中第[P1+1,P2]之间的基因复制到染色体O1的对应位置，获得子代染色体O1。

步骤5将F1和F2的位置交换，同理，可以得到后代O2。

如图5所示，对父代F1、F2执行交叉操作，选择交叉点P1=4,P2=8，按照以上方式执行交叉操作，得到子代O1、O2。

图5 染色体交叉示例

4.7 变异算子

为避免搜索过程过早地陷入局部最优，变异算子随机选择部分染色体的部分基因进行变异，具体步骤如下：

步骤1依据变异概率Pm和变异临时随机数Pmt的大小关系判断是否对该个体进行变异，若Pmt≤Pm(Pmt,Pm∈[0,1])成立，则对该个体进行变异操作，否则，不进行变异操作。

步骤2随机选择排放在玻璃原板的第k(k=1,2,…,colMax)列的所有玻璃原片进行变异，即选择染色体在区间[glaNumMax×(k-1)+1,k×glaNumMax]之间的基因进行变异。

步骤3随机生成一组可行的列订单组合替换排放在第k列的订单规格，得到变异后的染色体。一个可行列订单组合的生成步骤为：从切割订单中随机选择一个玻璃规格编号firstp，排放在第1个位置；在切割订单中寻找和firstp等长的所有玻璃规格的编号，存放在集合eql中；在等长订单规格集合eql中随机选择订单规格编号，排放在第[2,glaNumMax]个位置。

为避免种群收缩于局部最优解，又使种群进化保持一定的连续性，在进化过程中采用动态变异率。在进化的初级阶段，采用较高的变异率，使种群具有足够的突变性，避免收敛到局部最优解，而随着进化代数的提高，降低种群的变异率，避免种群无序化，使其在较优情况下向着最优解靠拢。取第t代个体的变异率Pm,t=N/(N+t)×Pm，其中Pm为最初设定的变异率，N为开始阶段设定的最大迭代次数，t为当前迭代次数。

4.8 精英保留策略

为加快算法的收敛速度，防止进化结果停滞不前或发生随机漫游现象，采用最优保留策略，即从本代染色体中选择适应度值最高的染色体中的一个，来取代子代染色体中适应度值最低的染色体中的一个。

4.9 算法整体流程

设P(t)为第t代种群，算法整体流程如下：

步骤1输入相关参数。输入浮法玻璃切割相关参数，即种群规模N(p)，交叉概率Pc，变异概率Pm，最大迭代次数N。

步骤2初始化种群。令t=0，产生个体数为N(p)的初始种群P(0)。

步骤3计算适应度函数值。根据缺陷分级参数、玻璃分级参数判定每块玻璃原片的质量等级，判定其单位面积的价格，进而计算第t代种群P(t)中每个个体的适应度函数值。

步骤4选择操作。采用随机按比例的方式，从P(t)中选择N(p)个个体复制到P(t+1)中。

步骤5交叉操作。依据交叉临时随机数Pct和交叉概率Pc的大小关系，Pct、Pc∈[0,1]，从选择操作所得种群中随机选择一对临时父代进行交叉，共进行N(p)/2次，产生N(p)个后代形成的临时种群。

步骤6变异操作。对于交叉操作产生的临时种群，依据变异临时随机数Pmt和当代变异概率Pm,t的大小关系，对个体进行变异操作，产生N(p)个后代形成新的后代种群。

步骤7最优保留策略。用P(t)中适应度函数值最大的一个个体取代P(t+1)中适应度函数值最小的一个个体。

步骤8令t=t+1，判断是否达到最大迭代次数，即若t=N，输出计算结果，结束程序；否则，转步骤3。

5 实例分析

5.1 实例说明

现有一块长12200 mm、宽4000 mm的浮法玻璃原板，经检测，该玻璃板面上共含有40个缺陷点，表2为各缺陷点的详细信息。已知缺陷等级参数DC={0.5,1.0,1.5,3,5}，玻璃分级参数QC={M1,M2,M3}，各等级玻璃单位面积的价格依次为11.2 元/m2，10.5 元/m2，9.6 元/m2，0元/m2，在该玻璃原板上切割表1所示订单规格，要求尽可能使获得的玻璃成品总价格最高。

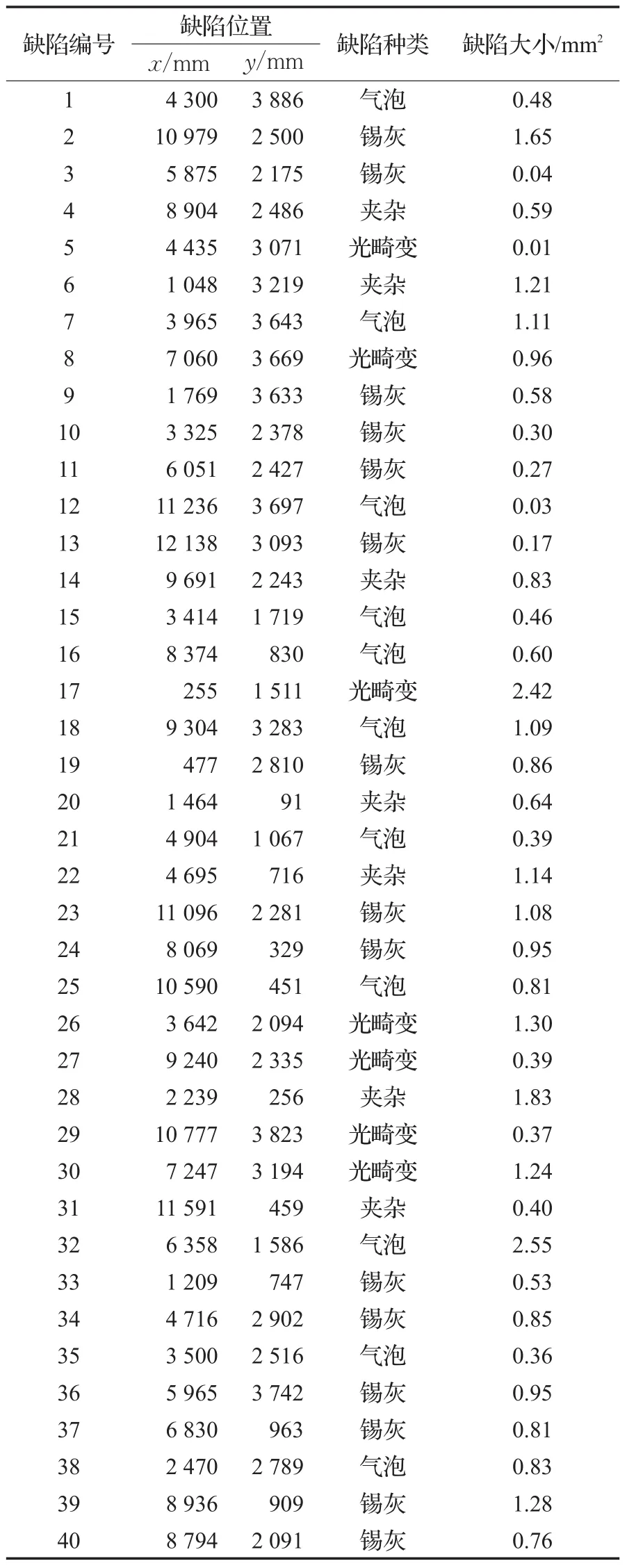
表2 缺陷信息

表3 实验结果统计

玻璃分级参数QC中M1、M2、M3的取值如下：

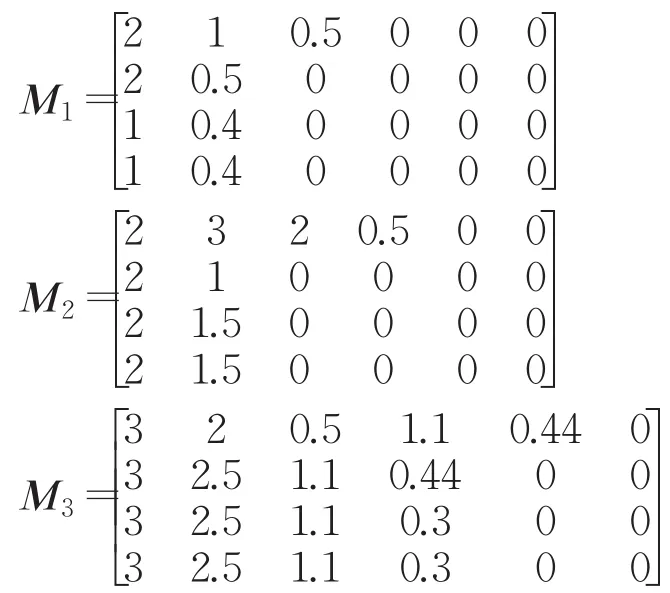
5.2 求解结果与分析

采用本文提出的改进遗传算法解决上述算例。令种群规模N(p)=10，迭代次数N=50，染色体交叉概率Pc=0.8，变异概率Pm=0.2。对遗传算法而言，其优化结果并不是唯一、确定的，因此针对以上浮法玻璃切割问题，将该遗传算法运行10次，计算结果见表3。

根据表3所示实验结果，可得出以下结论：

（1）对浮法玻璃优化切割问题而言，切割获得的玻璃成品块数越多，玻璃成品总价不一定最大。如：第1次和第2次实验均获得12块玻璃成品，但其玻璃成品的总价格均不是最大。

（2）切割获得的玻璃成品总面积最大，玻璃成品总价不一定最大。如：第6次实验获得的玻璃成品总面积最大，但其玻璃成品总价并不是最大。

（3）玻璃成品的总价是由玻璃成品面积和玻璃质量等级共同决定的。如：第7次实验获得10块玻璃成品，玻璃成品总面积为39.7788 m2，但其所得玻璃成品总价最大，是上述实验中的最佳方案。

以上10次实验中，第7次实验获得的玻璃成品总价最大，将该次实验对应的切割方案作为上述实例的最终切割方案，图6为最终切割方案的示意图。

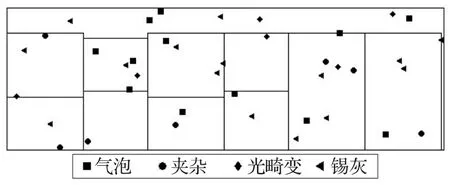
图6 玻璃原板缺陷信息及切割方案图示

5.3 算法性能比较

针对浮法玻璃优化切割问题，以玻璃成品总价格最大为优化目标，本文还提出了一种基于局部遍历的启发式搜索算法，该算法在保证排放在每个位置上的玻璃原片的质量等级最高的基础上，使其面积尽可能大，以保证排放每个位置的玻璃原片的价格最大。针对表4中6组不同的切割订单，将其优化结果与改进遗传算法进行比较。

由表5可知，和随机启发式算法相比，本文提出的改进遗传算法具有更好的性能，且针对一个确定切割订单和玻璃原板，随机启发式算法只能找到一组解决方案，而遗传算法每次运算可以获得最优解对应的多个解决方案，可以为规划人员提供多种选择。

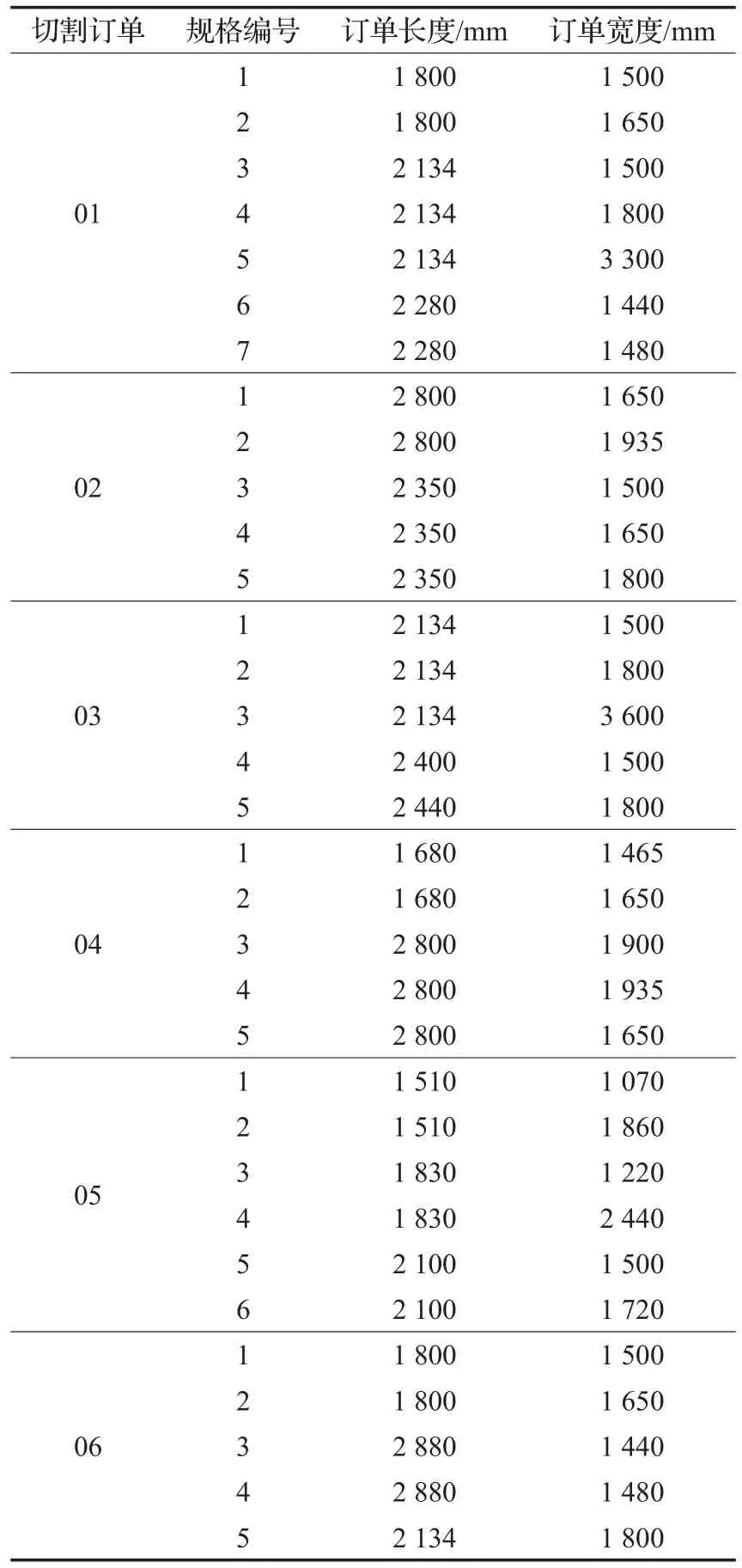
表4 切割订单

表5 算法优化性能对比

6 结束语

本文针对浮法玻璃切割问题，根据缺陷分级参数和玻璃分级参数对玻璃原片的质量等级进行判定，进而获得玻璃原片的价格，以玻璃成品总价最大为优化目标，建立该问题的数学模型，提出了一种基于玻璃原片排放位置编码的遗传算法。对算法的各个模块进行了设计，并以实例验证了所建模型的正确性及算法的有效性。实验结果表明：浮法玻璃的成品总价格是由玻璃成品面积和玻璃质量等级共同决定的，仅追求玻璃利用率最高或玻璃质量等级最高，均不能满足生产利益最大化的要求。本文提出的遗传算法，在一定程度上能够提高玻璃成品的销售价格，具有较好的性能。