地铁车辆受电弓上框架疲劳裂纹成因分析
2018-08-20欧昌宇吴积钦
欧昌宇 钟 源 吴积钦
(西南交通大学电气工程学院,610031,成都//第一作者,硕士研究生)
受电弓作为地铁车辆的重要元件,其良好的运行状态是列车安全运行的重要条件[1]。随着地铁的快速发展,刚性接触网得到广泛的使用,但问题也逐渐显露。由于长期工作在受限空间中并经受燃弧、电磁干扰等因素的影响,受电弓的一些关键部位在较短的时间内会出现裂纹[2-3],从而极大地影响列车安全运行。文献[3]指出,受电弓上框架肘接口处裂纹并非个例。
受电弓裂纹(见图1)的产生是一个复杂的过程,不仅与器件的材料、应力作用形式及大小有关,还与器件的结构及工作环境有关[4-5]。对此,一些学者针对受电弓裂纹的成因进行了研究。文献[6]通过有限元仿真和集中质量模型对TSG19型受电弓上框架裂纹进行了分析,认为受电弓模型的等效参数随着列车运行里程增加而退化,从而导致弓网性能的恶化,加剧裂纹产生。文献[2-3]则从受电弓的材料、焊接工艺方面对受电弓裂纹进行了简单分析,并提出了改进措施,但对裂纹产生的原因没有深入研究和试验验证。
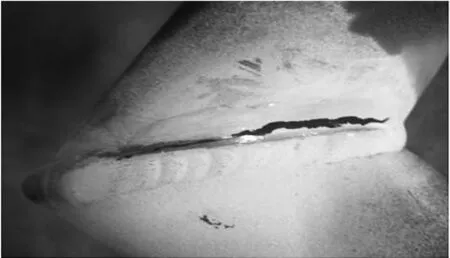
图1 受电弓上框架尾端肘部裂纹实景
文献[4]指出裂纹通常最先出现在应力大或者应力集中的部位,这些部位产生变形量比其它部位大,以致在交变应力作用下更容易产生初始裂纹。随着应力的继续作用,当应力产生的疲劳损伤积累到一定的程度时会导致器件失效。文献[7-8]通过仿真找出器件应力最大处和应力集中区域,并结合试验对器件的裂纹成因进行了分析,通过S-N曲线和Miner线性积累损伤理论对器件的寿命进行了分析。
本文以某型号地铁受电弓为例,通过仿真与试验相结合的方法对受电弓上框架裂纹进行分析,对比隧道内外接触网导高(4 600 mm与4 040 mm)下的估计寿命值,为地铁受电弓参数设计和优化提供参考。
1 材料分析与仿真结果
1.1 受电弓上框架材料
受电弓框架所使用的材料一般是热处理强化Mg-Al-Si系列合金。本文研究的受电弓上框架使用的材料是铝合金6082T6。铝合金6082T6具有中等强度、良好的焊接性能以及耐腐蚀性,其具体的化学成分见表1,相应的抗拉强度、屈服强度和硬度见表2。
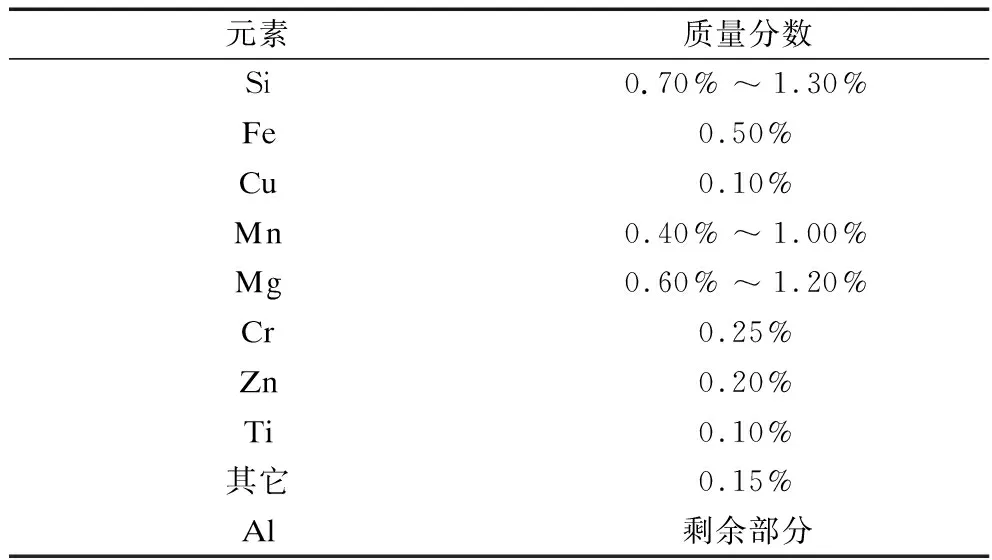
表1 铝合金6082T6各化学成分

表2 不同厚度(t)铝合金6082T6的力学参数
1.2 受电弓上框架有限元计算
裂纹常常出现在应力较大或集中的区域,因此,为了研究受电弓上框架的裂纹成因,首先需要确定受电弓上框架应力分布,以确定裂纹出现是否与应力有关。
根据试验所使用受电弓的尺寸,在ANSYS软件中建立受电弓几何模型,如图2所示。几何模型忽略了受电弓一些细节,如螺母、螺栓及一些不规则形状的影响。各活动关节均设置为铰接,而固定的面与面则视为固定连接。

图2 受电弓的计算模型
为模拟受电弓的工作情况,在下框架底部施加扭矩模拟升弓力矩,将弓头抬升,而弓头利用虚拟的弹簧进行限高和弓网接触力读取。整架受电弓被划分为72 351个网格和193 473个结点,其中上框架有21 377个网格和41 531个节点,如图3所示。
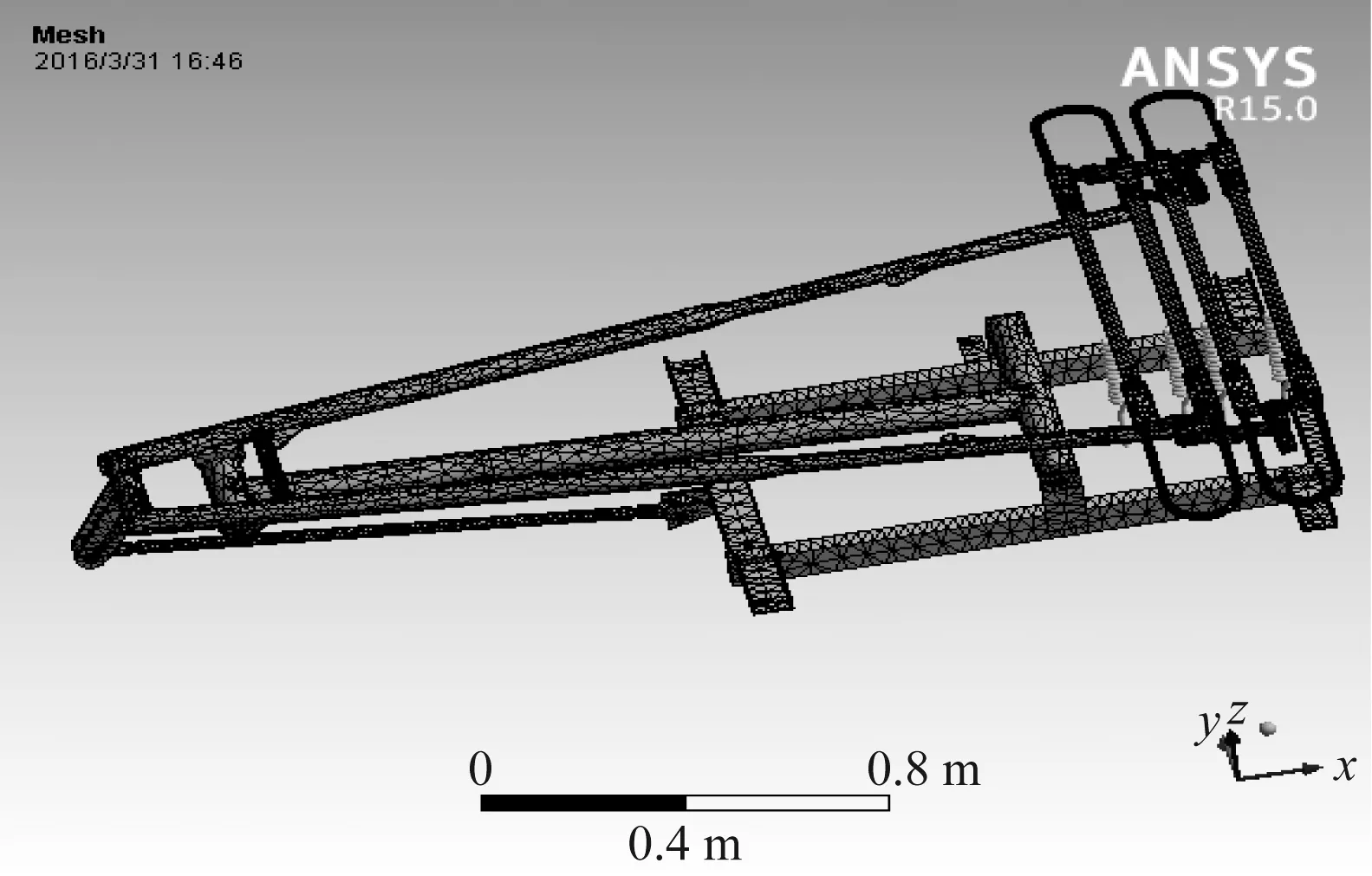
图3 受电弓网格划分
将弓头限制离原始位置220 mm处,并且将4个滑板下弹簧的力之和控制在120 N,即受电弓工作高度4 040 mm、弓网静态接触力120 N。此时,受电弓上框架的有限元计算结果如图4与图5所示,应力主要集中在上框架的肘部位置。上框架应力分布基本符合左右对称,但靠弓头一端的应力明显小于靠下框架一端,在尾端肘部应力值达到最大(83 MPa),并且集中在肘部焊缝周围。上框架尾端肘部应力主要是轴向拉伸应力,其作用方向基本垂直图1中裂纹扩展的方向。由此可见,应力多集中于受电弓肘部并且其方向垂直于焊缝。可以推断,受电弓裂纹的产生主要由应力集中引起。
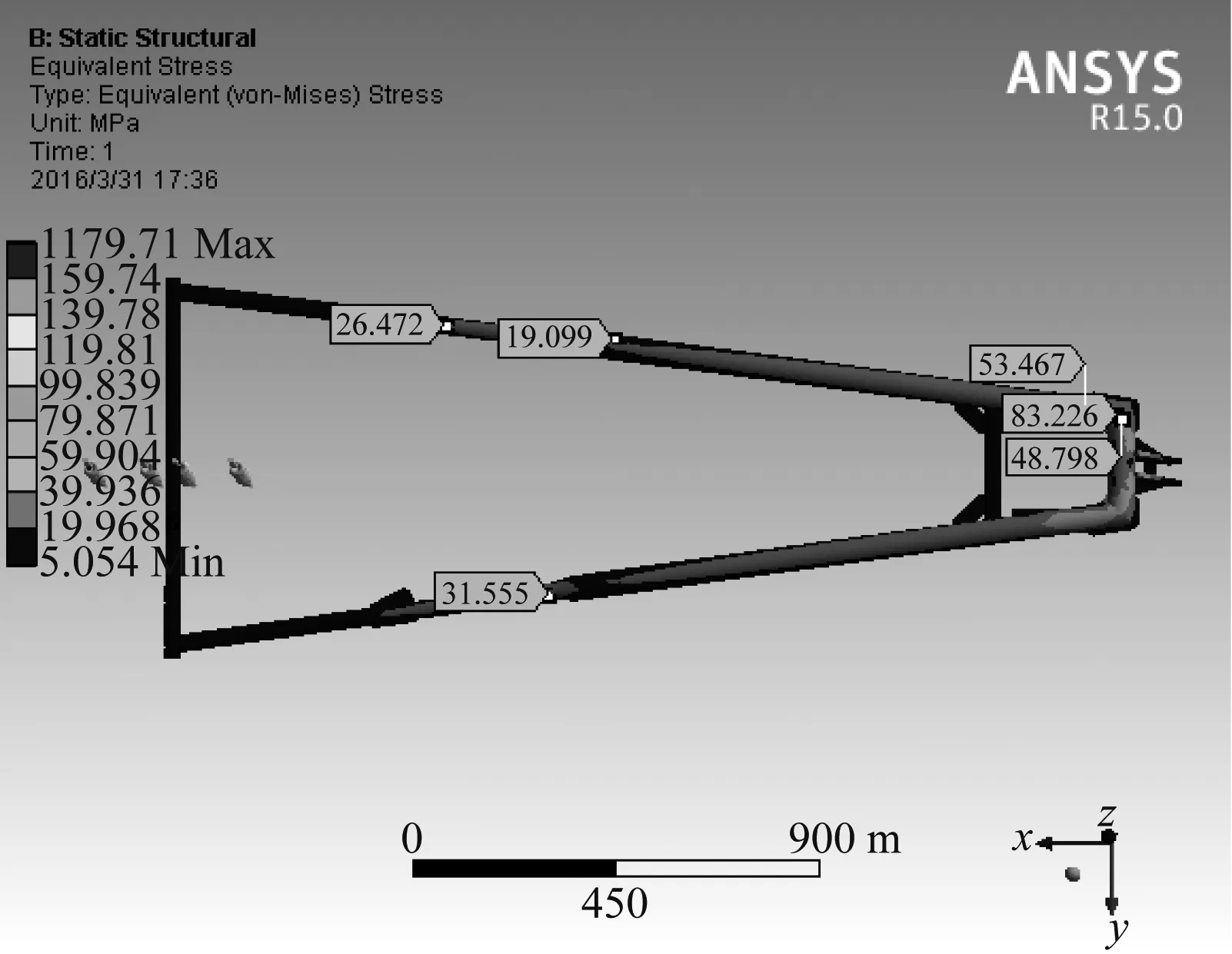
图4 受电弓上框架等效应力
2 试验测试及结果
2.1 试验设置
为验证有限元模型是否准确,需要测量受电弓实际应力情况。将该型号地铁受电弓固定于地面,通过调节气囊压力将静态接触力固定在120 N,并在受电弓上方设置限制装置,模拟受电弓实际工况。在室温条件下,测量不通电情况下的受电弓上框架应力。
试验选用电阻式应变计对受电弓上框架尾端肘部应力值进行测量。电阻式应变计结构简单、精度高、测量范围广,而受电弓没有电流作用,在合理的温度补偿条件下,使用电阻式应变计能够准确得到上框架尾端肘部的应力变化情况。根据图5所示的有限元计算结果,在受电弓上框架尾端肘部分别粘贴4枚电阻式应变计,其方向参见图5。
由于条件限制,试验以50 mm为增量,分别测量受电弓工作高度在3 890~4 390 mm范围内的应力值,得到应力与受电弓工作高度的关系曲线。
2.2 试验结果
试验采集的数据是1/4电桥电路的电压灵敏度系数Uo/U、Uo/U与测试点的轴向应变量ε有如下关系:
对式(1)变换得
式中:
K——应变计的灵敏度系数;
U——1/4电桥电路激励电压;
Uo——1/4电桥电路输出电压。
依据广义胡克定律中杆件应力与应变的关系,计算测试点的应力S如下:
S=E×ε
(3)
式中:
E——材料弹性模量,依据受电弓上框架所使用材料,取E=0.7×105MPa。
通过式(1)—(3),可由测量到的灵敏度系数计算4个测试点在各测试工作高度下的应力值,如图6所示。由图6可见,应力随工作高度的增加而呈线性减小,且测试点1、3的应力为正值,测试点2、4为负值。
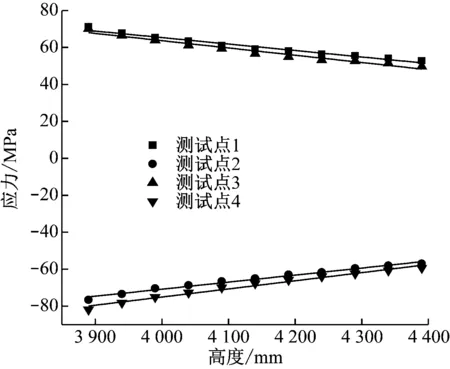
图6 受电弓上框架尾端肘部应力拟合曲线
将4个测试点的应力值进行线性拟合,可得到应力随高度的变化关系式:
式中:
S1、S2、S3、S4——测点1至4的应力,MPa;
h——受电弓工作高度,mm。
由式(4)可得,在工作高度4 040 mm时,测试点1至4的应力值分别为63 MPa、-69 MPa、61 MPa、-72 MPa,这与有限元模型计算得到的上框架尾端肘部应力基本相吻合。因此,可认为仿真结果可以反映受电弓上框架尾端肘部区域的应力分布情况。
3 疲劳寿命值估计
3.1 疲劳寿命分析
S-N曲线是疲劳强度与疲劳寿命之间的关系曲线,S-N曲线与器件的材料、形状、加工精度和热处理方式都有关系。S-N曲线在对数坐标系中应力S与应力循环作用次数N成线性关系,即S与N有如下关系:
式中:
S1 000——N为1 000次时的应力;
Sbe——屈服强度;
Nf——疲劳寿命极限。
文献[5]指出,铝合金没有一个真实的疲劳极限值,常规的做法的是以5×108循环次数作为铝合金的伪疲劳寿命极限值。而S1 000和Sbe与最终拉伸强度Su有如下关系:
S1 000=0.9Su
(6)
材料的疲劳极限Se.R与屈服强度Sbe有如下关系:
Se.R=SbeCLCDCSCR
(8)
式中:
CL、CD、CS、CR——分别为载荷因子、材料形状因子、材料表面因子、可靠度因子。根据本次试验的情况分别取CL=1.0、CD=0.78、CS=0.82、CR=0.9。
由式(5)—(8)并结合表2中材料的屈服强度,绘制出受电弓上框架尾端肘部的S-N曲线,如图7所示。
由图7中的S-N曲线,推导出应力作用次数N(疲劳寿命)与应力幅值S有如下关系:
N=ASb
(9)
式中:
A——疲劳强度系数;
b——疲劳强度指数。
依据S-N曲线推导出A的表达式为
(10)
疲劳强度指数b为S-N曲线在对数坐标下的斜率。将式(4)代入式(9),得到受电弓工作高度h与测试点应力作用次数N的函数:
Ni=A(cih+Bi)b(i=1,2,3,4)
(11)
式中:
ci、Bi——测试点1至4拟合直线的斜率和截距。
由此绘制出受电弓工作高度与上框架肘部疲劳寿命曲线,如图8所示。
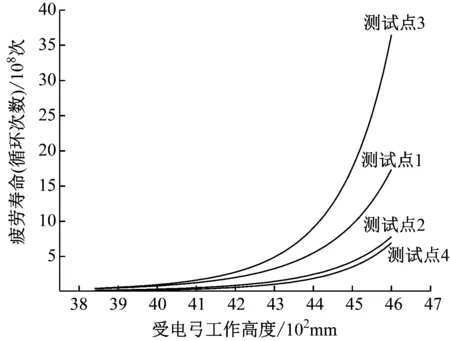
图8 疲劳寿命与受电弓工作高度变化曲线
由图8可以看出,受电弓上框架尾端肘部的疲劳寿命值与受电弓工作高度有密切关系,即受电弓工作高度越高,其寿命值越长,反之则越短。受电弓上框架测试点1至4在4 600 mm工作高度下的寿命值分别是在4 040 mm工作高度下的17.5、17.7、30.0、24.6倍。由此可见,在不考虑接触网弹性的情况下,长期工作在隧道外(4 600 mm)的受电弓寿命远大于工作在隧道内(4 040 mm)受电弓。如再考虑隧道外采用柔性接触网和隧道内采用刚性接触网的情况,则其寿命的差值将会更大。
3.2 算例分析
以文献[3]中所描述的受电弓上框架裂纹案例为实例进行分析。该线路除部分区段为地上线路,其余全部为地下线路。隧道内线路采用刚性接触网,其跨距按6 m布置。列车最高运行速度80 km/h。
受电弓振动属于随机振动,但在理想条件下,受电弓的振动可视为由接触网弹性的变化引起。接触网弹性以一跨为单位,呈周期变化。因此,取受电弓平均运行速度v=43 km/h,接触网平均跨距L=6 m,可以粗略地认为受电弓振动频率为v/L,则受电弓主要振动频率为2 Hz。地铁车辆每日运行时间段为6:30—23:30,但列车不是每时每刻都在运行,因此,对地铁车辆的运行时间做出每天8 h的假设,则在1日内受电弓所经历的振动估计为6×104次。地铁作为公共交通基本上每天都得运行,但列车有停运、检修等情况,因此,对地铁车辆做出1年运行300 d的估计,则在1年内受电弓经历的振动为1.8×107次。因测试点4的寿命值比其它3个测试点小,则以测试点4在工作高度为4 040 mm时的寿命值(2.8×107次)作为受电弓上框架尾端肘部的疲劳寿命极限值。依据Miner线性损伤积累原理,估计出尾端肘部出现裂纹的时间在1.5年左右,这与文献[3]中记载的裂纹出现时间基本符合。由此可见,受电弓上框架肘部裂纹主要是由于隧道内受电弓低工作高度所导致的应力集中造成的。
4 结论
本文对受电弓上框架应力情况进行了仿真分析与试验测试,通过对其结果的分析得到以下结论:
(1)受电弓上框架应力集中于肘部接口处,该处应力值随受电弓工作高度的上升而降低。长期工作在隧道内的低工作高度使该处应力集中而导致裂纹产生。
(2)根据应力与疲劳寿命、应力与工作高度的关系,建立了受电弓上框架肘部疲劳寿命与工作高度之间的函数,并由此计算得到隧道内工作的受电弓寿命是隧道外工作的1/30。
(3)通过算例对隧道内刚性接触网条件下的受电弓进行分析,发现其上框架肘部出现裂纹的时间为1.5年左右,与文献记载情况基本符合,进一步印证了分析结论。
对此,本文提出以下建议:
(1)适当加大受电弓的工作高度,以降低受电弓上框架肘部的应力;
(2)优化受电弓的结构,使上框架承受的应力减小;
(3)使用性能更优的材料或者增加上框架尾端肘部的厚度,以提高受电弓的疲劳寿命。
