嵌入式轨道竖向支撑刚度优化设计*

何远鹏 罗信伟 焦洪林 杨 刚 韩 健 赵 悦 肖新标

(1. 西南交通大学牵引动力国家重点实验室， 610031， 成都； 2. 成都市新筑路桥机械股份有限公司， 611430， 成都；3. 广州地铁设计研究院有限公司， 510010， 广州//第一作者，硕士研究生)

嵌入式轨道是有轨电车的常用轨道。这种轨道沿纵向连续的支承方式大大降低了由于传统离散支承的不平顺性引起的轨道结构振动，并通过槽型轨周围的弹性材料变形耗能，减振降噪性能良好，稳定性好，养护维修量少，特别适用于有轨电车线路轨道，在国外有轨电车系统中已有应用先例[1-2]。嵌入式轨道的槽型轨与道床的连接方式不同于传统的轨道结构中离散的扣件连接方式，它是在混凝土整体道床中设置一个凹槽，槽型轨放置在凹槽内，以高分子弹性材料敷设至槽型轨的轨头下方将槽型轨固定。有轨电车系统钢轨支撑刚度影响因素多元化，影响因素包括浇筑填料弹性模量、密度，承轨槽尺寸，轨垫板弹性模量、密度、厚度，PVC管尺寸直径等槽内结构参数，从而导致支撑刚度对嵌入式轨道动力学性能的影响存在差异。

文献[4]对嵌入式轨道的稳定性进行了分析，得到了嵌入式轨道在稳定性上的优越性；文献[5]对比分析了嵌入式轨道与扣件式轨道在动力学上的差异，并指出了嵌入式轨道在动态响应上的优势；文献[6]建立了嵌入式轨道振动与噪声模型，对比分析了现有嵌入式轨道、优化后的嵌入式轨道以及普通板式轨道，得出优化的嵌入式轨道能降低噪声4～6 dB；文献[7]使用波数有限元-边界元法对嵌入式轨道振动与噪声进行了响应计算，对比分析了嵌入式轨道与普通轨道的降噪效果，对于600 Hz以上的振动噪声，嵌入式轨道的降噪效果比较明显。以上国内外学者都对嵌入式轨道进行了深入的对比分析研究，但是并没有针对给定的嵌入式轨道形式给出最优材料参数建议。

本文主要针对新式嵌入式预制轨道板结构，建立有限元模型，分析影响承轨槽支撑刚度的因素以及竖向支撑刚度的范围，并建立有轨电车-嵌入式轨道耦合动力学模型，分析承轨槽填充材料支撑刚度对嵌入式轨道系统动态特性的影响，得到竖向刚度的合理范围，从而可以选取相应的材料参数得到最优的竖向刚度。

1 嵌入式轨道有限元模型

为了调查影响钢轨竖向支撑刚度的因素以及竖向刚度的影响范围，本文建立了包含槽型轨、高分子浇筑填料、轨垫板、PVC管、嵌入式轨道板等关键因素的嵌入式轨道有限元模型，如图1所示。

图1 嵌入式轨道有限元模型

有限元模型所用的基本参数为新筑路桥机械股份公司的嵌入式轨道设计参数。在基本参数的基础上进一步调查参数的变化范围，分析其对钢轨支撑刚度的影响，参数调查的范围如表1所示。

表1 影响钢轨竖向支撑刚度的主要参数及其变化范围

2 有轨电车-嵌入式轨道耦合动力学模型

在明确了钢轨竖向支撑刚度的影响因素和影响范围之后，进一步建立有轨电车-嵌入式轨道耦合动力学模型，调查合理的刚度取值范围，从而优选出基于动力学性能的承轨槽内结构参数。

2.1 车辆系统模型

根据车辆动力学理论[8-9]，有轨电车系统可简化为由车体、摇枕、构架、轮对/轮组(动车为传统轮对，拖车为独立轮组)和两系悬挂系统组成，其动力学模型如图2所示。车体与构架用二系悬挂连接，而轮对轴箱和构架间则用一系悬挂连接。

根据达朗贝尔原理，对有轨电车车辆子系统各部件进行受力分析，可求得车辆各部件之间的相互作用力，从而建立并求解车辆系统各部件的运动微分方程。本文所建立的有轨电车整车系统[5]由3个车体、3个转向架构架、2个摇枕、4个传统轮对、2个独立轮组轴桥、4个独立车轮等组成，整个车辆子系统共有76个自由度。

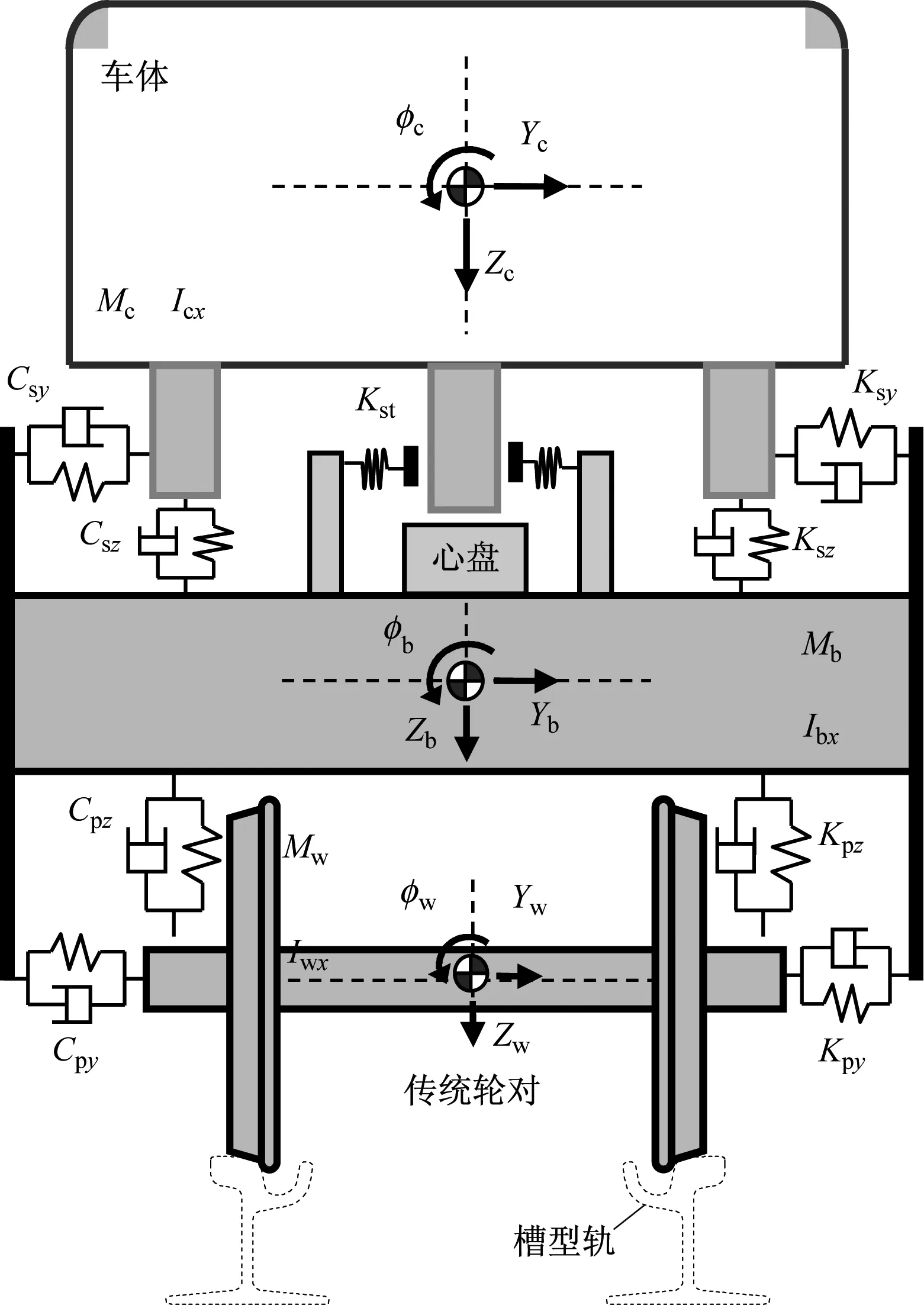
图2 有轨电车动力学模型

2.2 轨道系统动力学模型

嵌入式轨道由槽型轨、承轨槽填充材料、轨道板及其以下基础组成，如图3所示。通过对嵌入式轨道动力学性能进行调查，给出的嵌入式轨道动力学计算模型见图4。其中，左右槽型轨被视为连续弹性支承基础上的Timoshenko梁，考虑钢轨的竖向、横向和扭转振动，轨道板用三维实体有限元单元模拟。槽型轨填充材料用三维粘弹性弹簧-阻尼单元模拟，轨道板以下基础的支撑效果用等效的弹簧/阻尼单元模拟。

图3 嵌入式轨道结构

图4 嵌入式轨道动力学模型

2.3 轮轨空间接触模型

轮轨空间动态接触几何关系的求解思路参考 “新型轮轨空间接触几何关系”计算模型[10]。轮轨接触点的确定采用迹线法[11]和最小距离法。针对新津线有轨电车车辆的车轮踏面外形，采用SY8型踏面，钢轨采用59R2槽型轨。轮轨空间动态接触力模型包括轮轨法向力计算模型和轮轨切向力计算模型两部分。轮轨法向力采用Hertz非线性弹性接触理论求解；关于轮轨蠕滑力的计算，首先以Kalker线性蠕滑理论计算[12]，轮轨间蠕滑达到饱和后，采用Shen-Hedrick-Elkins理论进行非线性修正[13]。

3 结果与分析

3.1 填充材料对竖向刚度影响分析

根据所建立的嵌入式轨道有限元模型，加载竖向载荷，计算得到实际参数情况下的钢轨竖向支撑刚度为127 kN/mm，与实测值一致，证明了利用本文所建立的有限元模型计算钢轨竖向支撑刚度是有效的。

图5给出了钢轨竖向支撑刚度随着浇筑填料弹性模量改变的变化曲线。由图5可见，钢轨竖向支撑刚度随着浇筑填料弹性模量的增大而增大，呈随着弹性模量的增大刚度变化的趋势变平缓，填充材料弹性模量浮动值从-5～3 MPa，相应地，竖向支撑刚度的变化范围为40～150 kN/mm，增大接近4倍。

图5 浇筑填料弹性模量对钢轨竖向支撑刚度的影响

图6给出了钢轨竖向支撑刚度随着轨垫板弹性模量改变的变化曲线。由图6可见，钢轨竖向支撑刚度随着轨垫板弹性模量的增大而增大，轨垫板弹性模量浮动值从-4 Mpa增加到4 Mpa，则钢轨竖向支撑刚度从80 kN/mm增加到150 kN/mm(增大近2倍)。

图7给出了钢轨竖向支撑刚度随着PVC管直径改变的变化曲线。由图7可见，随着PVC管直径值的增加，钢轨竖向支撑刚度先缓慢减小，再缓慢增大，在管直径浮动值为0～10 mm附近存在极小值，约为127 kN/mm；在管直径浮动值30 mm附近钢轨竖向支撑刚度取得最大值，约为129 kN/mm。与浇筑填料和轨垫板的弹性模量影响相比，PVC管直径变化对钢轨竖向支撑刚度的整体影响不大。

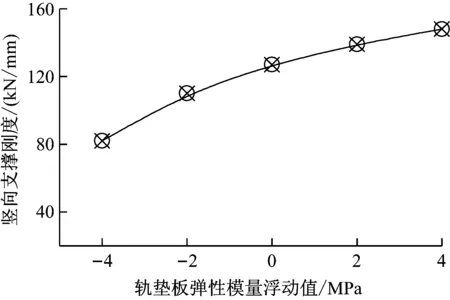
图6 轨垫板弹性模量对钢轨竖向支撑刚度的影响

图7 PVC管直径对钢轨竖向支撑刚度的影响

图8给出了钢轨竖向支撑刚度随着承轨槽深度改变的变化曲线。由图8可见，钢轨竖向支撑刚度随着承轨槽深度的增大而减小，且减小趋势随着深度的增大而变缓，呈现非线性关系。承轨槽深度由-10 mm增加到10 mm，钢轨竖向支撑刚度从180 kN/mm降低到100 kN/mm。

图8 承轨槽深度对钢轨竖向支撑刚度的影响

图9给出了钢轨竖向支撑刚度随着承轨槽宽度改变的变化曲线。由图9可见，钢轨竖向支撑刚度随着承轨槽宽度的增大而减小，且减小趋势随着承轨槽宽度的增大而变缓，呈现非线性关系；随着承轨槽宽度从-20 mm增加到+20 mm，钢轨竖向支撑刚度从136 kN/mm降低到126 kN/mm。

图9 承轨槽宽度对钢轨竖向支撑刚度的影响

通过图8、图9的对比可知，承轨槽深度变化对钢轨竖向支撑刚度的影响比宽度变化的影响更为明显。

综上所述，PVC管直径、承轨槽宽度对钢轨竖向支撑刚度影响不显著，而浇筑填料弹性模量、轨垫板弹性模量以及承轨槽深度对钢轨竖向支撑刚度影响较大。由图5可见，通过更改浇筑填料弹性模量可得钢轨竖向支撑刚度的最小值为40 kN/mm。由图8可见，通过更改承轨槽深度可得钢轨竖向支撑刚度的最大值为180 kN/mm。本文钢轨竖向支撑刚度取值范围为40～180 kN/mm。

3.2 典型工况下嵌入式轨道动力特性

列车以70 km/h速度在直线轨道上运行，轨道谱选用随机不平顺激励，承轨槽填充材料的横向刚度为52 kN/mm，竖向刚度为127 kN/mm，横向阻尼为9 kN·s/m，竖向阻尼为11 kN·s/m。图10和图11分别给出了随机不平顺激励下的钢轨和轨道板的动力响应结果。

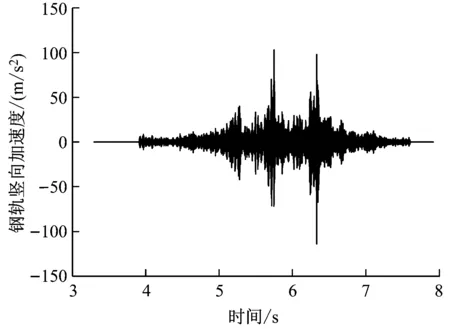
a) 钢轨竖向加速度

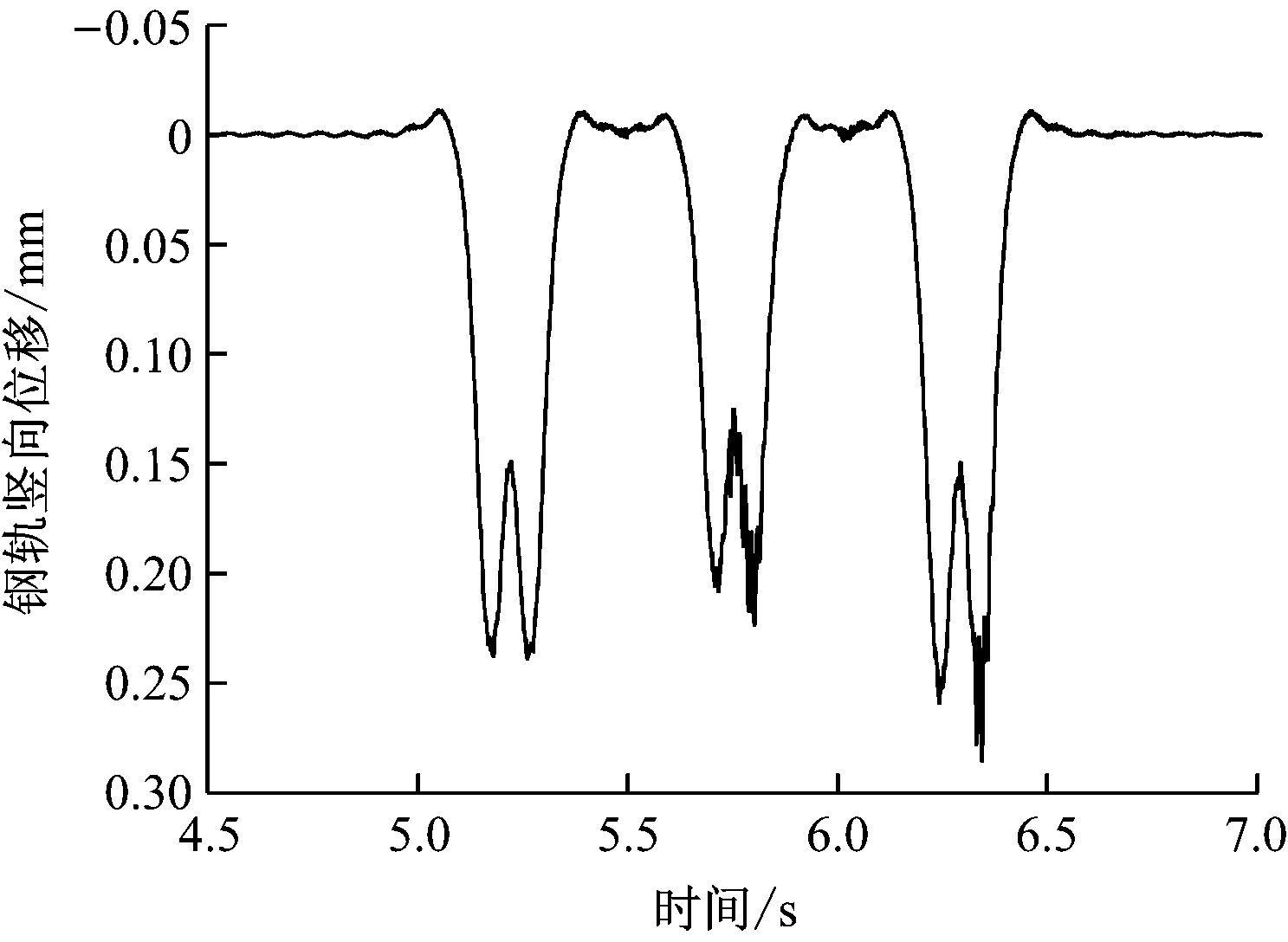
b) 钢轨竖向位移图10 钢轨竖向加速度与位移

a) 轨道板竖向加速度

b) 轨道板竖向位移图11 轨道板竖向加速度与位移

由理论分析并结合图10 a)可知，从5 s后第一个转向架开始通过观察点，随后第2、第3个转向架依次通过观察点，第1、2、3个转向架通过时激励起来的最大钢轨加速度依次为40 m/s2、103 m/s2、112 m/s2。由此可得，钢轨的最大加速度发生在最后一个转向架离开观察点时。理论分析并结合图10 b)可知，当第一个轮对通过观察点时，钢轨先向上翘曲，翘曲高度为0.01 mm，而第1、2、3个转向架通过观察点时，钢轨最大位移依次为0.24 mm、0.22 mm、0.29 mm，即钢轨的最大位移发生在第3个转向架离开观察点时。

由理论分析并结合图11可知：轨道板竖向加速度最大值 8 m/s2出现在第2个转向架通过观察点时；当第一个转向架通过观察点时，轨道板发生向上翘曲，翘曲高度为0.008 mm，而第1、2、3个转向架通过观察点时，轨道板最大位移的依次为0.05 mm、0.045 mm、0.056 mm，可以看出轨道板的最大位移发生在第3个转向架离开观察点时。

以本节计算工况为参考工况，在此基础上选用不同的钢轨竖向支撑刚度，调查钢轨竖向支撑刚度对轨道动力响应的影响。根据对钢轨竖向刚度的影响因素调查可知，竖向支撑刚度的取值范围在40～180 kN/mm，故以此范围作为刚度取值范围。选取轨道结构各响应的最大值作为对比目标，分析钢轨竖向支撑刚度的改变对其产生的影响。

3.3 钢轨竖向支撑刚度对轨道动力特性的影响

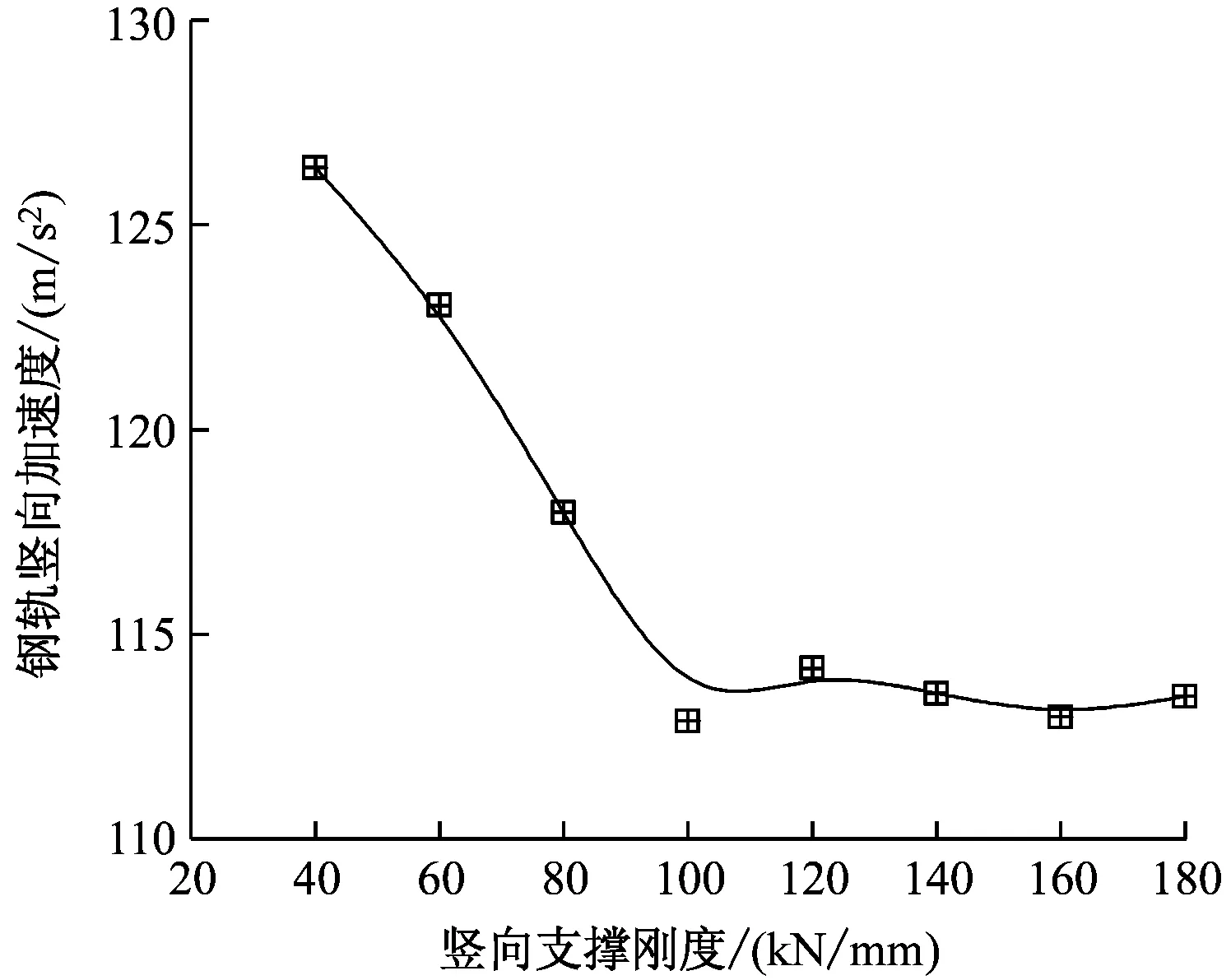
图12给出了嵌入式轨道动力响应随着钢轨竖向支撑刚度改变的变化情况。由图12可见：钢轨的竖向加速度和位移均随着钢轨竖向支撑刚度的增大而减小，当钢轨竖向支撑刚度达到100 kN/mm时，钢轨竖向加速度和竖向位移变化趋于平缓；轨道板的竖向加速度和竖向位移均随着钢轨竖向支撑刚度的增大而缓慢增大，且幅值较小。综合考虑钢轨竖向支撑刚度对钢轨和轨道板竖向动态特性的影响，钢轨竖向支撑刚度取值范围选择在100 ～ 140 kN/mm内较为合适。

a) 钢轨竖向加速度

b) 钢轨竖向位移

c) 轨道板竖向加速度

d) 轨道板竖向位移图12 钢轨竖向支撑刚度对嵌入式轨道动力响应的影响

结合钢轨竖向支撑刚度最优取值范围可知，在原有参数基础上，浇注填料弹性模量浮动值建议为0～2 MPa，轨垫板弹性模量浮动值取为-2～2 MPa，承轨槽深度浮动值取为0～10 mm，而PVC管直径和承轨槽宽度对钢轨竖向刚度影响不大。

4 结语

本文调查了钢轨竖向支撑刚度的影响因素，结果表明浇筑填料弹性模量、轨垫板弹性模量、承轨槽深度对钢轨竖向支撑刚度影响显著，而PVC管直径、承轨槽宽度对钢轨竖向支撑刚度影响不大。同时，建立了有轨电车-嵌入式轨道耦合动力学模型，初步分析了嵌入式轨道结构的动力学特性，并调查了钢轨竖向支撑刚度对轨道动态特性的影响，给出了基于轨道动力学特性的钢轨竖向支撑刚度的合理性取值范围为100～140 kN/mm。根据钢轨竖向支撑刚度的合理取值范围，在原有参数基础上，浇注填料弹性模量浮动值建议取为-1～1 MPa，轨垫板弹性模量浮动值取为-2～2 MPa，承轨槽深度浮动值取为0～10 mm。