平面三向织物复合材料增强体顶压性能有限元分析

2018-08-20，，，

材料科学与工程学报 2018年4期

，，，

(江南大学生态纺织教育部重点实验室，江苏无锡 214122)

1 引言

纤维增强复合材料通常是由纤维增强体和树脂基体组成的，由于其具有高的比模量和比强度，低的密度、以及可设计性强等优点，在航空航天领域得到越来越广泛的应用[1-2]。纤维增强体在复合材料中作为主要承载体承受更多的载荷作用，因此，纤维增强体的力学性能在更大程度上决定了复合材料的力学性能[3-4]。平面三向织物是由三组互成60°夹角的纱线彼此交织而成的一种织物[5-6]，该织物具有很好的准各向同性，采用树脂与其复合可得到一种具有准各向同性、质量较轻的复合材料结构[7-8]。

张天阳等[9-11]对机织物顶破过程进行有限元分析，研究顶破过程中机织物的应力应变分布、能量吸收机制以及摩擦作用的影响。赵磊等[11-13]对三维机织增强复合材料弹道顶压边缘部分进行有限元分析，研究了子弹在三维机织增强复合材料中应力波的传播过程，对比分析子弹顶压后边缘部分的实验结果和模拟计算结果，并对三维机织增强复合材料的最终破坏模式与常用层合板进行比较。孙汉健[14]对不同结构纺织复合材料进行准静态侵彻实验分析及有限元模拟，研究以纯铝 MTS 实验数据为标定，分析了准静态侵彻载荷—位移曲线及其破坏机理，比较了不同结构纺织复合材料以及纯铝的位移—载荷曲线，由此计算得到位移与吸能关系曲线；同时根据复合材料各自织物中纤维束排列及织物成型特点，分别建立了复合材料的细观结构模型和单胞模型。

本文通过ANSYS有限元模拟软件，对用于复合材料增强体的平面三向织物和平纹织物在恒定静态载荷作用下的力学行为进行分析，并进行两种织物的力学行为对比。

2 建立模型

2.1 结构参数假设

平面三向织物增强复合材料是由织物增强体和树脂基体共同构成的材料，故材料在承受载荷时，平面三向织物和树脂基体的作用机理十分复杂。为减少工作量并进行有效的模拟，根据对织物细观结构观察，本文在构建模型时对平面三向织物做出一些理想化的假设[15]：

(1)织物中的纱线被看做是凸透镜形截面的均质体，忽略纱线中长丝之间的空隙；(2)假设纱线的表面是均匀且平滑的。纱线表面的粗糙程度由纱线间摩擦系数来表征；(3)初始状态下，所有经纱和纬纱之间是紧密接触的，交织点处没有空隙。

2.2 建立模型

借助PRO/E构建出平面三向织物和平纹织物的结构模型。纱线凸透镜型截面尺寸通过放大测量按比例计算得到，如图1所示。通过扫描中心线的方式绘制出纱线模型，并通过装配功能将纱线按平面三向织物和平纹织物的交织规律固定在一起(如图2所示)，其尺寸为直径为20mm和厚度为0.58mm(图2(a)、(b))的平面三向织物与平纹织物实物图(图2(c)、(d))的对比。构建出冲头的结构模型，冲头是一个直径为5mm的球形模型。

图1 纱线截面图Fig.1 Yarn cross section

图2 平面三向织物(a,c)和平纹织物(b,d)结构模型Fig.2 Plane tri-axial fabric (a,c) and plain fabric (b,d) structure model

3.1 材料参数

平面三向织物、平纹织物和冲头的材料定义如下：组成织物的纱线为锦纶纤维制成的纱线，冲头材料是钢，两种材料的主要参数如表1，织物参数如表2所示。

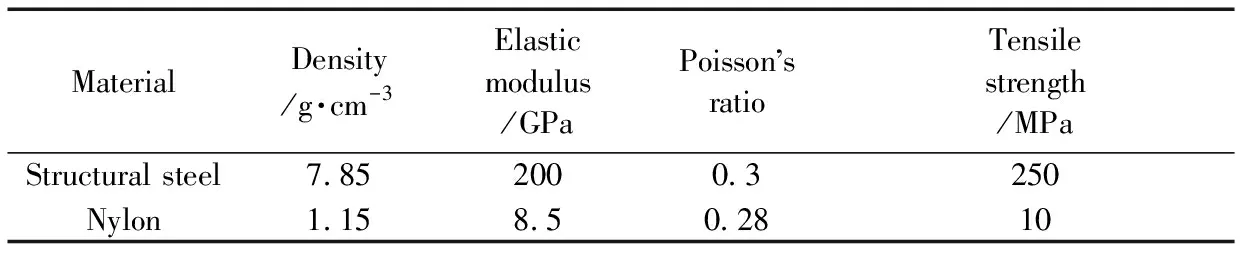
表1 冲头和试样材料参数Table 1 Punch and sample material parameters

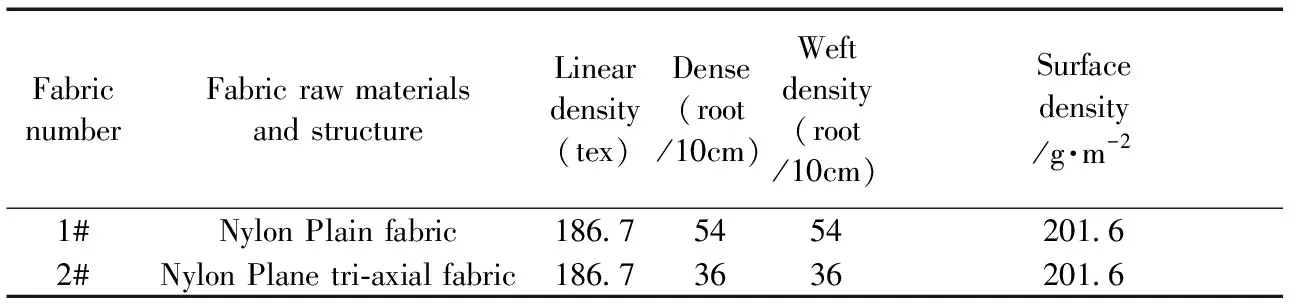
表2 平面三向织物和平纹织物结构参数Table 2 Triaxial fabric and plain weave fabric structure parameters

3.2 网格划分和施加载荷

将建立织物的结构模型导入分析软件ANSYS，借助布尔运算将其中的纱线连接为一个整体，平面三向织物的几何结构比较复杂，因此采用四面体单元对平面三向织物(图3a)和平纹织物(图3b)模型进行网格划分[4]。

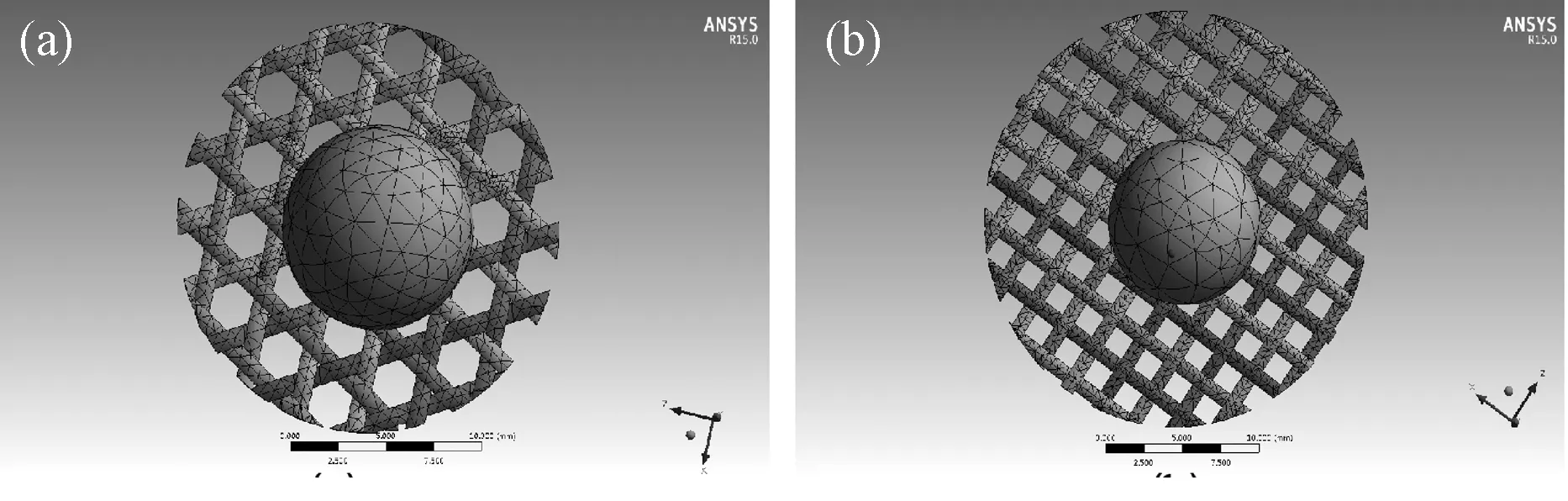
图3 平面三向织物(a)和平纹织物(b)网格划分Fig.3 Mesh Classification of the plane tri-axial fabric (a) and the plain weave fabric (b)

其中，平面三向织物的Nodes和Elements分别为16516和7274，平纹织物的Nodes和Elements分别为16788和5501构成。对平面三向织物和平纹织物添加约束，纱线的截面添加Fixed Support完全固定约束；结合前人实验和模拟分析结果，对冲头添加Pressure压力载荷，其中x方向、z方向为0MPa，y方向分别施加0.2、0.4、0.6及0.8MPa载荷，探究同一载荷同样面密度下，平面三向织物和平纹织物的变形、应力及弹性应变的差异和不同载荷下织物应力、弹性应变和织物形态变化规律。

4 结果与分析

4.1 顶压形变

图4 平面三向织物顶压变形云图Fig.4 Top pressure deformation nephogram of the plane tri-axial fabric

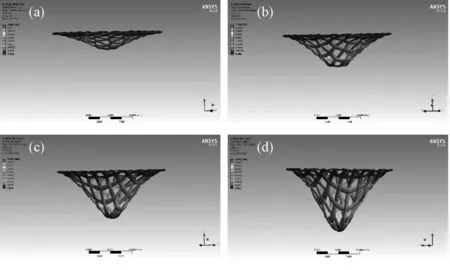
图5 平纹织物顶压变形云图Fig.5 Top pressure deformation nehogram of the plain fabric

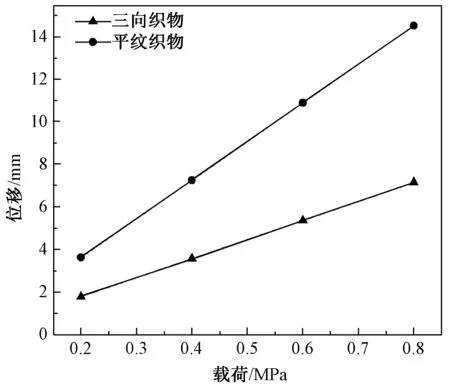
图6 平纹织物和平面三向织物变形载荷-位移关系图Fig.6 Deformed load-displacement of plain weave fabric and plane tri-axial fabric

平面三向织物和平纹织物顶压形变云图分别如图4和图5所示，图4和图5中(a)、(b)、(c)和(d)分别代表平面三向织物和平纹织物在承受0.2、0.4、0.6及0.8MPa载荷作用下织物变形云图，可以看出随着载荷的增加织物变形程度加大。但可以看出在同一载荷下两种织物的变形有明显的差异，平纹织物的变形相对较大。

平面三向织物和平纹织物的变形载荷-位移图如图6所示，可以看出在同样载荷下平纹织物的位移变形是平面三向织物位移变形的2倍左右，这是因为平面三向织物在承受载荷时，载荷可以沿着6个方向分散，在更多的方向起到分解载荷的作用，相反平纹织物在承受载荷时，载荷只能沿着经纬纱的4个方向分散载荷，从而导致织物在承受同样载荷时位移变形不同。

4.2 顶压应力

分别对平面三向织物和平纹织物在恒定静态载荷下的应力分布进行模拟，结果分别如图7和图8所示。

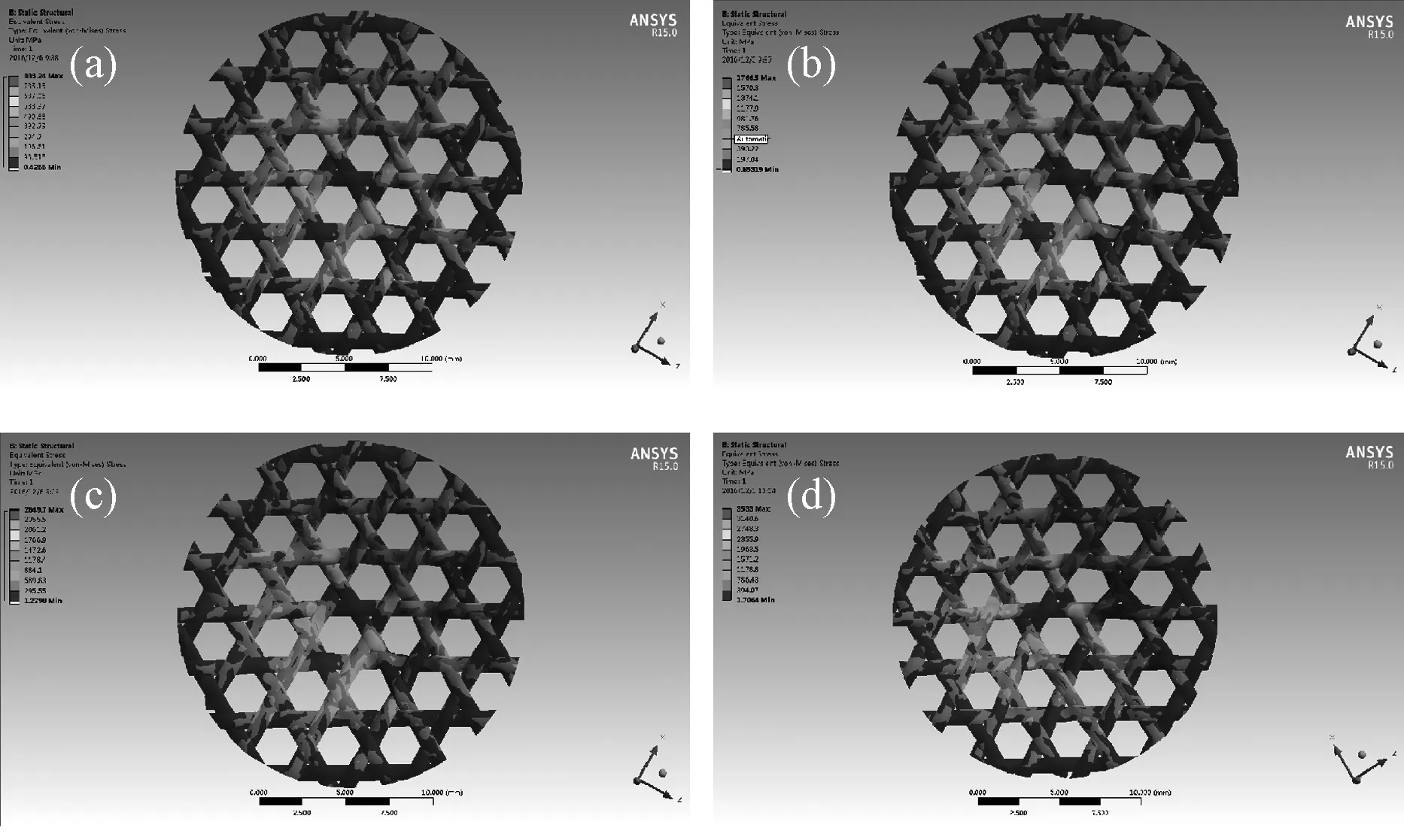
图7 平面三向织物顶压应力云图Fig.7 Top pressure stress nephogram of the plane tri-axial fabric

图8 平纹织物顶压应力云图Fig.8 Top pressure stress nephogram of the plain fabric

图7、图8中(a)、(b)、(c)和(d)分别代表平面三向织物和平纹织物在0.2、0.4、0.6和0.8MPa载荷作用下的应力分布云图，可以看出平面三向织物和平纹织物在受到冲头顶压的部位与织物的边缘相比应力相对较大，这是因为与冲头接触的部分承受较大的载荷，而在其周围未与冲头接触部位承受的载荷较小；两种织物中，平面三向织物的应力分散得比较均匀，平纹织物的应力则集中于与冲头接触的部位。

选取织物应力应变云图中的最大应力和最小应力，绘制平面三向织物和平纹织物应力-载荷曲线见(图9和图10)，其中图9表示两种织物在不同载荷下织物的最小应力，图10表示两种织物在不同载荷下织物的最大应力。由图9可知，在同样载荷作用下平纹织物的最小应力是平面三向织物的10倍左右，例如在0.4MPa载荷下三向织物最小应力是0.85319MPa，而平纹织物最小应力是7.335MPa。图10所示平面三向织物和平纹织物最大应力值基本一致。

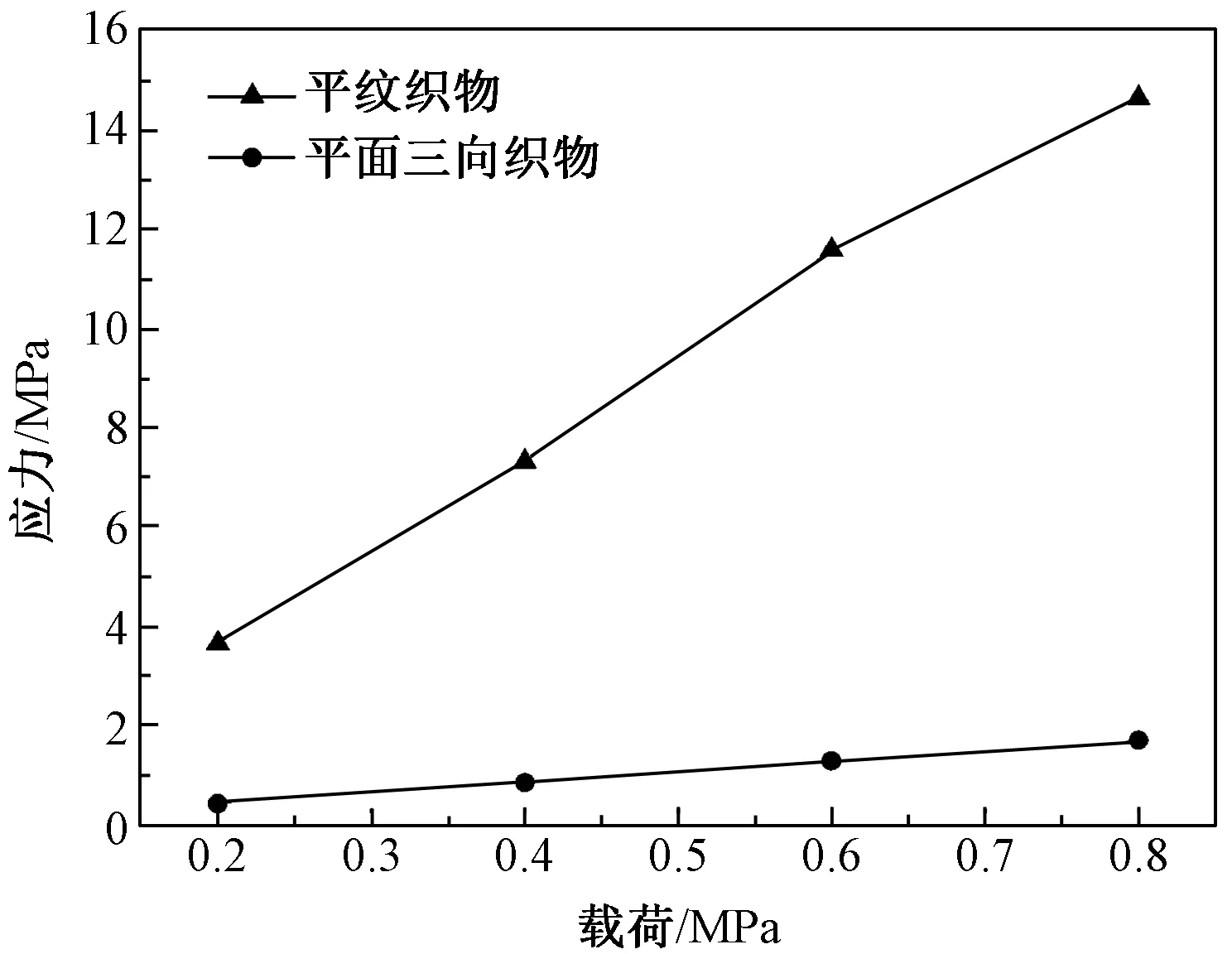
图9 平面三向织物和平纹织物最小应力-载荷曲线Fig.9 Minimum Stress-Load curves of the plane tri-axial fabric and the plain fabric

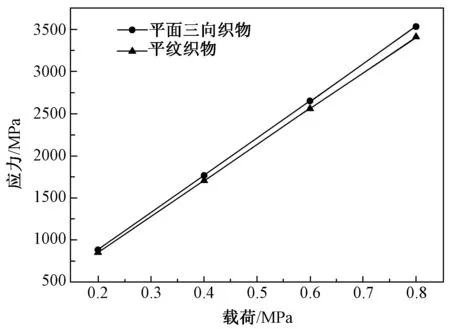
图10 平面三向织物和平纹织物最大应力-载荷曲线Fig.10 Maximum Stress-Load curves of the plane tri-axial fabric and the plain fabric

原因分析：从图7和图8中可以看出在织物与冲头接触的部位，织物中产生的应力最大，此时织物承受的载荷最大且没有出现载荷分散的现象，因此两种织物应力基本一致。但当载荷沿着纱线方向向边缘分散过程中，平面三向织物分散的方向较多，而平纹织物只能沿着经纬两个方向分散载荷，分散的方向较少。因此，平面三向织物较平纹织物具有更好的抵御破坏的能力。

4.3 顶压应变

分别对平面三向织物和平纹织物在恒定静态载荷下的应变分布进行模拟，结果如图11和图12所示，图11、图12中(a)、(b)、(c)和(d)分别代表的是载荷为0.2、0.4、0.6和0.8MPa作用下平面三向织物和平纹织物的应变分布云图。在图11中，可以看出冲头与织物直接接触的部分比未与冲头接触部位的织物应变较小。而在图12中可以看出,织物与冲头直接接触部分的应变较为明显，而边缘部分的应变相对较小。

图11 平面三向织物顶压应变云图Fig.11 Top pressure strain nephogram of the plane tri-axial fabric

图12 平纹织物顶压应变云图Fig.12 Top pressure strain nephogram of the plane fabric

由以上分析可知，平面三向织物和平纹织物的应变变化趋势基本一致，但也存在着差别，如图13和图14所示，图13表示平面三向织物和平纹织物在载荷作用下最小的顶压应变，可以看出在同样载荷作用下平纹织物的顶压应变大于平面三向织物，并且相差近10倍左右。图14代表平面三向织物和平纹织物在载荷作用下最大的顶压应变，图示在同样载荷作用下平纹织物和平面三向织物顶压应变基本一致。

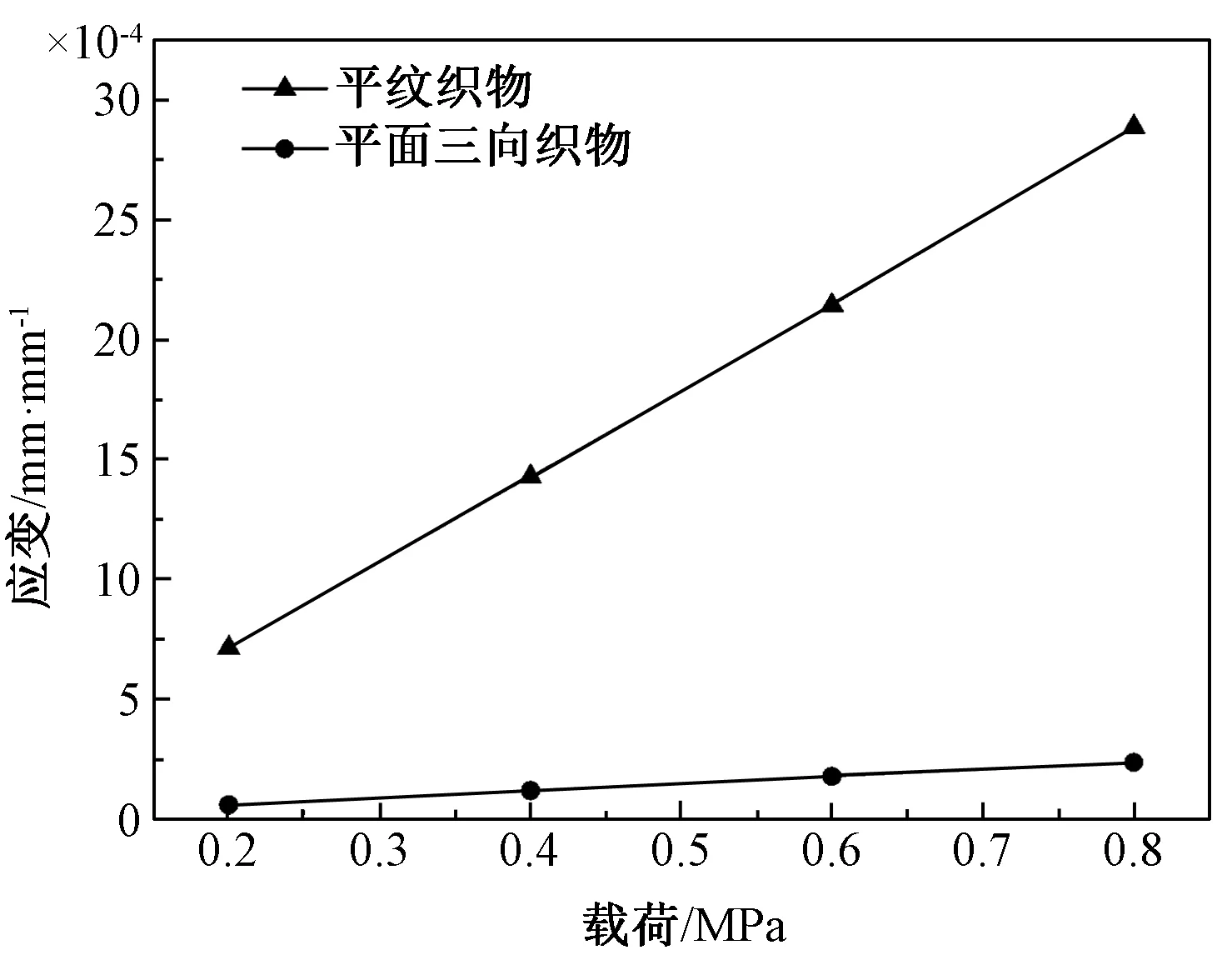
图13 平面三向织物和平纹织物最小应变-载荷曲线Fig.13 Minimum Strain-Load curves of the plane tri-axial fabric and the plain fabric

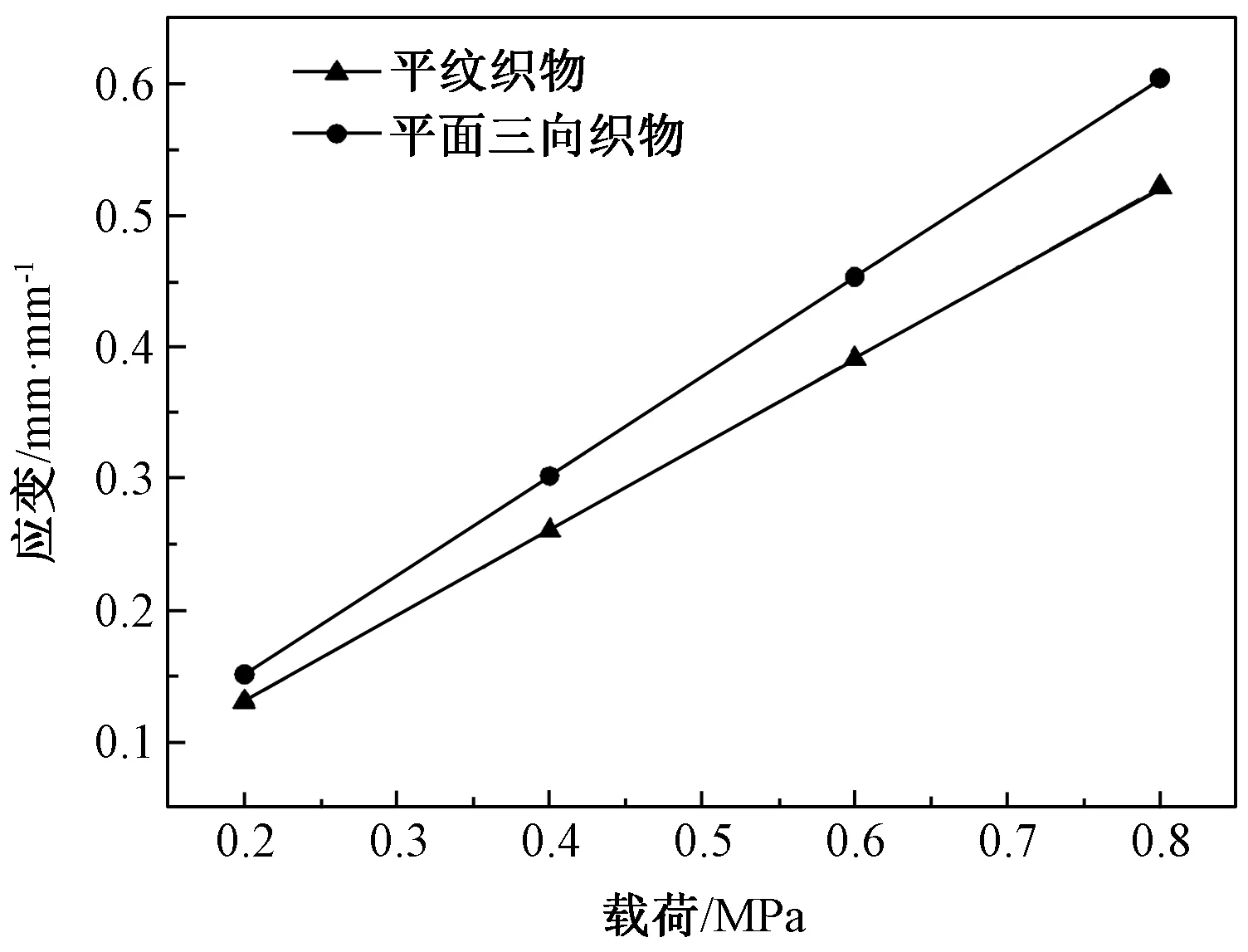
图14 平面三向织物和平纹织物最大应变-载荷曲线Fig.14 Maximum Strain-Load curve of the plane tri-axial fabric and the plain fabric

原因分析：在恒定静态载荷作用下冲头与织物直接接触的部位，织物产生的顶压应变最大，由于平面三向织物和平纹织物都是和冲头接触，受载荷直接作用，因此此时在同样载荷下顶压应变一致。但在织物与冲头没有接触的部位，由于平面三向织物在承受载荷时，载荷分散比平纹织物均匀，当载荷传递到织物边缘时，平面三向织物产生的顶压应变就小得多，相反平纹织物在承受载荷时，载荷只能沿着织物经纬纱的方向传递，当载荷传递到织物边缘时的顶压应变相对较大。