LCD缺陷检测系统的图像压缩感知方法
2018-08-20黄建军
冯 奇 黄建军 张 源 赵 斌
(1. 深圳大学信息工程学院,广东深圳 518060; 2. 深圳市华星光电技术有限公司,广东深圳 518132)
1 引言
随着数字成像技术和集成电路的迅猛发展,高清LCD屏作为液晶电视、笔记本电脑、桌面显示器、智能手机等产品的核心部件,正向着大画面、低功耗、轻薄化、高分辨率的方向发展,主流的全高清屏(FHD)物理分辨率达到了1920×1080,而为满足更高视觉需求的4K屏、8K屏也已投入生产。高清屏的生产过程相当复杂,受工艺、设备、人工和环境等因素的影响,屏幕表面容易形成划痕、破裂、崩边、亮斑、脏污、灰尘、指纹等各种缺陷。为提升高清屏的良品率,这些缺陷的检测和识别至关重要。而现有的人工缺陷检测效率低、人为误差大,已不再适应急速增长的生产需求;在工业视觉检测领域,基于机器视觉的表面缺陷检测逐渐成为主流,有着广泛的应用,如纺织物污损检测、 LCD表面检测、钢表面擦伤检测等[1-2]。
传统的LCD缺陷检测系统先利用高清CCD摄像机对缺陷屏进行完整的数字图像采集,再进行图像分割、特征提取和缺陷识别等后续处理。但随着高清屏的尺寸和分辨率增大,摄像机的分辨率也要随之增大,导致用于缺陷检测的图像数据量激增,以4K屏为例,分辨率3840×2160,真彩色32位,每帧将产生近31.6 MB的数据,这对现有缺陷检测系统的实时图像采集、传输、处理提出了极高的要求。
压缩传感(Compressive Sensing,CS)[3- 4]是一种在采集的同时进行压缩的新技术,只要信号是稀疏的,就可以用低于奈奎斯特率的采样重构出原始信号。高清LCD缺陷图像正是一种稀疏信号,其稀疏性体现在两个方面:首先缺陷在图像中的分布是稀疏的,即缺陷出现的概率较低且缺陷在图像中所占的面积较小,一般是点缺陷如亮点、暗点,线缺陷如暗线、亮线,或者是面缺陷如块Mura、环Mura等;其次待检测图像一般是规则的(等间隔、灰度均匀),而缺陷是不均匀、异常的,容易在特定的变换域中稀疏表示。因此,有学者开始研究将CS应用于缺陷检测。Xie[2]从纹理分析的角度对表面检测技术进行了深入的研究;李清勇等[5]提出了缺陷检测的稀疏表达模型,用两个冗余字典分别表示图像背景和缺陷目标,然后借鉴盲源分离法实现缺陷的分解;王宪保[6]等改进了K-SVD算法用于图像缺陷检测;杨晓霞等[7]根据超声相控阵的成像方法,得到了压缩传感下的腐蚀缺陷图像;王辉等[8]采用稀疏低秩分解实现了铝箔图像的缺陷检测;Cen Yigang等[9]利用低秩矩阵恢复实现了TFT-LCD图像不同类型缺陷的检测;Wang X等[10]采样背景恢复和多通道混合检测方法有效完成了TFT-LCD图像的Mura缺陷检测。尽管上述研究成功地将压缩感知技术应用于图像的缺陷检测,但现有的研究主要集中在缺陷稀疏表示、缺陷图像去噪、缺陷边缘检测、缺陷分割、缺陷特征提取等方面,都回避了如何利用压缩感知获取图像的问题。
针对压缩感知的具体实现,本文提出了一种适用于LCD缺陷图像的压缩感知方法,该方法对高清缺陷图像先行压缩采样后列压缩采样,很好地利用了高清LCD缺陷图像的整体稀疏特性,以较少的采样实现了高分辨率成像,极大地减少了采样数据量,不仅能加快信号的实时处理,还能提高信号的压缩率。
2 行列分离压缩感知方法
2.1 压缩感知理论

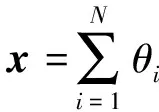
(1)

压缩感知理论指出,可以将稀疏信号x与测量矩阵Φ=[φ1,φ2,…,φM,…,φN]∈RM×N相乘,得到压缩测量向量y∈RM,即:

(2)
其中A∈RM×N为感知矩阵。常用的测量矩阵有高斯随机矩阵、伯努利随机矩阵、循环矩阵等。为保证信号重构效果,A必须满足有限等距特性(Restricted Isometry Property, RIP)[3],即:
(3)
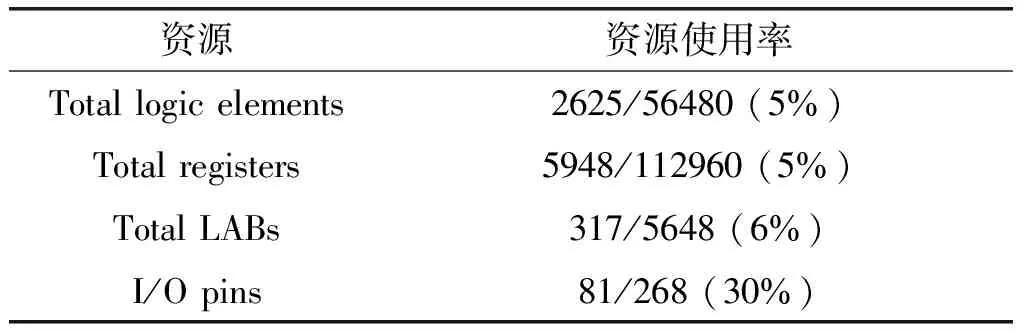
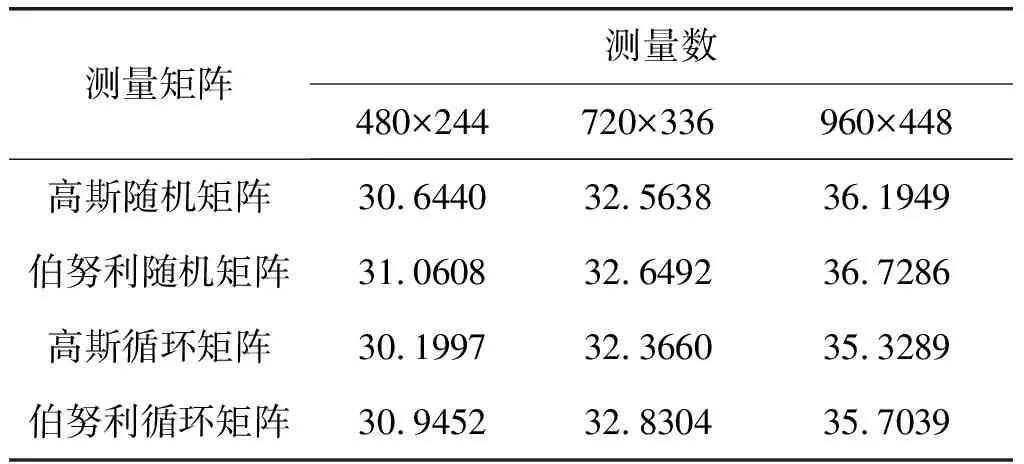
信号重构是压缩感知的核心,即用长度为M的测量向量y重构长度为N(M< (4) 现有压缩感知方法在处理图像信号时,一般是直接CS或者分块CS。直接CS的方法会导致测量矩阵非常庞大,大大增加了压缩测量和信号重构的计算复杂度;而分块CS的方法忽视了图像信号整体的稀疏性,增加了压缩测量和信号重构的次数,使得压缩和重构的效率变低,且块效应似的重构效果变差。为解决上述问题,本文提出了一种高效的LCD缺陷图像压缩感知方法,该方法使用两个不同的测量矩阵对图像的行、列数据先后进行压缩测量,再利用这两个矩阵的等效测量矩阵对信号进行整体的重构。具体过程如下: 设LCD缺陷图像X=[xi j]M×N是稀疏信号,缺陷所占像素点少,在空间域具有稀疏性,对一帧大小为M×N的图像,采用如下的过完备稀疏基: (5) 用行测量矩阵Φ=[φi j]L×N对X的每一行分别做压缩测量,得第i行压缩测量向量: (6) (7) 则有: B=XΦT (8) 用列测量矩阵Θ=[θij]K×M对B的每一列分别做压缩测量,得第j列测量向量: yj=[yi j]K×1=Θ×[b1j,b2j,…,bMj]T (9) (10) 由式(8)、(10)得Y=ΘB=ΘXΦT。 该方法大大减小了测量矩阵的规模,降低了测量过程的复杂度,提高了压缩效率,易于硬件实现。而且这种先按行测量的方法正好匹配了传感器逐行逐像素输出图像信号的模式。 设x∈RMN为X按行堆叠得到的列向量,y∈RKL为Y按行堆叠得到的列向量,则有: y=(Θ⊗Φ)x (11) 因此行列分离压缩感知方法实质上是对信号整体做压缩测量,既减小了测量矩阵的规模,又充分利用了信号的稀疏性,提高了压缩效率。 FPGA具有真正的硬件并行性,处理速度非常快,其现场可编程的特性允许开发者快速修改和升级设计,FPGA厂商提供的大量IP核也降低了开发难度、缩短了开发周期。因此本文采用FPGA设计了针对高清屏缺陷图像的行列分离压缩感知电路,从硬件实现角度说明提出方法的可行性和实用性。 行列分离压缩感知FPGA方案框图如图1所示,主要包括3个模块,压缩采样模块(CS)、控制模块(Control Unit)和图像转置存储模块(Image Transpose RAM)。压缩采样模块分时复用,完成图像的行压缩采样和列压缩采样;图像转置存储器模块暂存CS模块的行采样结果;控制模块主要负责将CS模块的行压缩采样结果写入存储器,并将存储器中的数据按列输送到CS模块实现列压缩采样。另外还有两个复选器SEL1和SEL2, SEL1选择把图像或者存储器中的行压缩采样结果作为CS模块的输入,SEL2选择把CS模块的压缩采样结果输出到存储器或外部端口。 图1 行列分离压缩感知FPGA方案框图 若观测矩阵的值随机为1或-1,则一维信号的压缩采样可以简化为加减运算过程,因此可以直接使用累加器计算。 压缩采样模块具体电路如图2所示,累加器ACC采用FPGA厂商提供的IP核,H是M位的循环左移移位寄存器,用于存储值为1或0(电路中替代-1)的随机伯努利向量。Y是N个16 bit寄存器组成的移位寄存器,存储累加器ACC输出的压缩采样值。所有累加器的数据输入端口都相同,其加减控制端口分别连接到移位寄存器H中的一位。寄存器中存储的0或1值即低电平或高电平控制累加器对输入数据累减或累加。累加器的数据输出端口连接到寄存器Y。 采集一帧分辨率为3840×2160的高清LCD缺陷图像,M=3840,N=960,即在行压缩采样时每行3840个数据获得960个观测值。在列压缩采样时,只使用移位寄存器H中的2160位和448个ACC,即每列2160个数据获得448个观测值,压缩比约5%,即(960×448)/(3840×2160)。 该模块采样前先将伯努利随机向量装载到移位寄存器H,然后在同步时钟的控制下,等data端口将采样数据逐个输入到所有ACC后,使移位寄存器H循环左移,通过H中存储的高低电平控制与其连接的ACC累加或累减输入数据,等一行(列)数据全部输入完毕,此时累加器的输出就是该行(列)数据的压缩采样结果,最后把采样值写入寄存器Y再逐个输出。 压缩采样模块中的ACC1仿真波形如图3所示,其中H(1)控制着ACC1的累加累减运算,data是输入数据,ACC1_Sum是累加器的输出。H(1)为0时,ACC1累减data;H(1)为1时,ACC1累加data。等一行数据输入完毕,ACC1的输出就是压缩采样值Y(1)。移位寄存器和累加器的相互协调工作实现了观测矩阵对信号的压缩采样。 图2 压缩采样模块 图3 ACC1仿真波形 表1 图像转置存储模块接口信号说明 图像转置存储模块的FPGA内部存储器由Altera的ALTSYNCRAM IP核定制生成。其接口信号如图4和表1所示,采用简单的双端口模式,写操作从data端口写入数据,读操作从q端口读出数据。其作用是将按行压缩采样获得的数据依次写入存储器,然后再按列读出。对一帧分辨率为3840×2160的高清LCD缺陷图像,经过行压缩采样,每行数据获得960个观测值,即获得960×2160个数据,把行压缩采样的数据写入存储器,每写入一个数据,地址加1;列压缩采样时需要把按行存储的数据再按列读出,所以每读出一个数据,地址增加960。 压缩采样模块和图像转置存储模块负责处理数据,二者独立或协同工作时需要遵循一定的逻辑顺序,这一顺序由控制模块负责完成。由于压缩采样和数据输出电路在某些阶段同时工作,因此需要设计两个并行的状态机。 图4 图像转置存储模块接口信号 压缩采样状态机如图5所示,其中idle是默认初始状态;waitR表示等待行起始信号,即等待一行有效数据的输入;CS1表示行压缩采样,在此状态完成一行数据的压缩采样。一帧图像数据行压缩采样完毕则进入wRam状态,此状态表示等待行压缩采样数据的数据全部写入存储器,而具体的写入工作由数据输出状态机控制。CS2代表列压缩采样,waitC代表等待下一列数据。数据输出状态机如图6所示,默认初始状态也是Idle;WrRam表示把行压缩采样数据写入存储器;WaitNextRow表示等待下一行数据;WaitCS2表示等待列压缩采样完成;Output状态表示把列压缩采样数据按照一定的时序输出。 结合状态机和各模块的电路结构图总结整个行列压缩感知电路的详细工作步骤如下: 1)检测到图像的起始信号后,随机伯努利向量被同步加载到移位寄存器H。 2)图像数据被逐行逐个输入到所有的累加器,在时钟信号的触发下每输入一个数据,H就循环左移一位,H中存储的高低电平控制累加器的累加或累减。 图5 压缩采样状态机 图6 数据输出状态机 3)一行图像数据全部输入完成后,行压缩采样值即所有累加器的输出数据被写入到移位寄存器Y,再被逐个写入到图像转置存储模块。 4)控制模块重新装载随机伯努利向量到H,并对所有累加器模块的输出清零。 5)重复2)、3)、4)步骤,直到所有行(一帧图像)的数据输入完毕。 6)控制模块将图像转置存储模块中的行压缩采样数据按列读出,并逐个输入到压缩采样模块。 7)压缩采样模块的累加器再次对输入数据进行累加或累减运算,每输入一个数据,H也循环左移一位。 8)一列数据全部输入完成后,控制模块将这一列数据的压缩采样值即所有累加器的输出数据写入到Y,然后再逐个输出。 9)控制模块重新装载随机伯努利向量到H,并对所有累加器模块的输出清零。 10)重复6)、7)、8)、9)步骤,直到所有列的数据都已经从图像转置存储模块读出。 为了方便采集从FPGA输出的压缩采样数据,信号必须依照一定的时序输出。如图7所示,在数据输出状态机控制下,控制模块提供了高电平有效的帧同步信号和行同步信号,分别表示一帧数据和一行数据的起始。 图7 同步信号波形 行列分离压缩感知FPGA电路经过综合、映射、布局、布线生成分析报告,FPGA电路逻辑资源的消耗情况如表2所示。本文使用的5CGXBC7C6U19C7芯片是Altera公司CycloneV系列中的一款高端FPGA芯片,最高支持500 MHz的时钟,由表2可以知道该电路只消耗了5%的逻辑资源。该电路另外采用了一片128 MB的SDRAM作为外部缓存,若采集一帧分辨率3840×2160的灰度图像,压缩采样电路的行测量值缓存器最大需要存储16位的3840×960的数据,即7.03 MB。该电路采用图像信号时钟297 MHz,对一帧图像完成行列采集耗时约10 ms,完全满足实际需求。该电路处理速度快,消耗逻辑资源少,具有很好的实用性。 表2 FPGA逻辑资源消耗统计 为了验证行列分离压缩感知方法的有效性,本节设计了两个仿真实验。实验一采用不同的压缩率对同一高清LCD缺陷图像进行采样,比较不同的压缩比对图像重构质量的影响。实验二在压缩比恒定的情况下,验证行列分离压缩感知方法是否能采集高清LCD图像不同类型的缺陷。实验采用的高清屏缺陷图像分辨率都为3840×2160,行测量矩阵和列测量矩阵采用相互独立的同类测量矩阵,信号重构采用主流的正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)算法。 以一帧相同的高清LCD缺陷图像作为原始待采集图像,测量数分别采用480×244、720×336、960×448,对应的压缩率约为1.29%、2.92%、5.19%。每种压缩情况都分别选取高斯随机矩阵、伯努利随机矩阵、高斯循环矩阵和伯努利循环矩阵作为测量矩阵。测量完成后,用OMP算法对每次得到的压缩测量值进行图像重构。采用信号峰值信噪比PSNR来衡量重构图像的质量,表3的每个PSNR值都是50次实验的平均值。 表3 不同压缩率重构图像的PSNR 实验结果表明重构图像的平均峰值信噪比随着观测数的增加显著增大,当PSNR达到35时,重构图像基本没有失真,重构效果较好。因此当测量数为960×448,即压缩率为5.12%时,由四类不同测量矩阵获得的测量值都能较好地重构原始信号。使用不同测量矩阵、相同测量数重构的信号平均信噪比接近,说明对于行列分离压缩感知方法,这几种不同的测量矩阵的重构效果基本相同。 高清LCD屏缺陷主要分为点缺陷、线缺陷、面缺陷,本实验选取一帧包含这三种缺陷的典型缺陷LCD屏表面图像,如图8所示。采用伯努利循环矩阵作为测量矩阵,该矩阵由值为1或-1的随机伯努利向量循环移位生成。实验测量数为960×448。首先对图8行列压缩采样,再对其进行重构,重构图像的PSNR均值为35.8184。由于原始图像和重构图像分辨率过高,为清晰展示不同类型缺陷的细节,首先对原始图像和重构图像的缺陷部分进行裁剪放大,再针对不同类型缺陷的局部原始图像和重构图像,选用相同的阈值进行二值化处理,实验结果如图9所示。可以看出,行列压缩采样方法在满足一定的压缩率后,可以不失真地采集不同类型的图像缺陷,图像细节信息基本没有丢失。 图8 缺陷LCD屏的表面图像 本文针对压缩感知的具体实现和高清屏缺陷检测系统中缺陷图像采集、存储、传输数据量大的问题,提出了一种适用于LCD缺陷图像的压缩感知方法,其FPGA方案不仅充分利用了图像信号整体的稀疏性,还大大减少了测量矩阵的规模,简化了电路实现,提升了压缩率;通过等效测量矩阵实现了图像的整体重构,保证了重构效果,具有很好的实用性。 需要指出的是,尽管本文采用了离散数字图像作为输入,但实际中可以通过随机解调[15]等AIC方式直接对图像传感器输出的视频行信号进行压缩采样,再对得到的数字信号进行列压缩采样。本文是CS在图像处理实际应用中的一次新尝试,为后续的应用研究提供了一种新思路。 [1] Li Yadong, Gu Peihua. Free-form surface inspection techniques state of the art review[J]. Computer-Aided Design, 2004, 36(13): 1395-1417. [2] Xie Xianghua. A review of recent advances in surface defect detection using texture analysis techniques[J]. Electronic Letters on Computer Vision and Image Analysis, 2008, 7(3):1-22. [3] Candes E, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly imcomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. [4] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory,2006, 52(4): 1289-1306. [5] 李清勇, 梁正平, 黄雅平,等. 缺陷检测的稀疏表示模型及应用[J]. 计算机研究与发展, 2014, 51(9):1929-1935. Li Qingyong, Liang Zhengping, Huang Yaping, et al. The sparse representation model of defect detection and its application[J].Computer Research and Development, 2014, 51(9): 1929-1935. (in Chinese) [6] 王宪保, 章国琼, 姚明海. 稀疏编码改进方法及其在缺陷检测中的应用研究[J]. 小型微型计算机系统, 2017, 38(1):165-168. Wang Xianbao,Zhang Guoqiong,Yao Minghai. Improved Sparse Coding Method and its Application in Defect Detection[J]. Journal of Chinese Computer Systems, 2017, 38(1):165-168. (in Chinese) [7] 杨晓霞, 薛彬, 靳世久,等. 压缩传感在超声相控阵检测系统中的应用研究[J]. 电子测量与仪器学报, 2015, 29(9):1286-1294. Yang Xiaoxia, Xue Bin, Jin Shijiu, et al. Application study on compressed sensing in ultrasonic phased array detection system[J]. Journal of Electronic Measurement and Instrument, 2015, 29(9):1286-1294. (in Chinese) [8] 王辉, 孙洪. 鲁棒主成分分析的铝箔表面缺陷检测方法[J]. 信号处理, 2017,33(4): 577-582. Wang Hui, Sun Hong. Robust Principal Component Analysis for Aluminum Foil Surface Defects Detection[J]. Journal of Signal Processing, 2017,33(4): 577-582. (in Chinese) [9] Cen Yigang, Zhao Ruizhen, Cen Lihui, et al. Defect Inspection for TFT-LCD Images Based on the Low-rank Matrix Reconstruction[J]. Neurocomputing, 2015, 149(3): 1206-1215. [10] Wang X, Dong R, Li B. TFT-LCD mura defect detection based on ICA and multi-channels fusion[C]∥Information Science and Control Engineering (ICISCE), 2016 3rd International Conference on. IEEE, 2016: 687- 691. [11] Chen S S, Donoho D L, Saunders M A. Atomic Decomposition by Basis Pursuit[J]. Siam Review, 2001, 43(1):129-159. [12] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655- 4666. [13] Needell D, Tropp J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]. Applied & Computational Harmonic Analysis, 2009, 26(3): 301-321. [14] Blumensath T, Davies M E. Iterative hard thresholding for compressed sensing[J]. Applied & Computational Harmonic Analysis, 2009, 27(3): 265-274. [15] Kirolos S, Laska J, Wakin M, et al. Analog-to-Information Conversion via Random Demodulation[C]∥Design, Applications, Integration and Software, 2006 IEEE Dallas/CAS Workshop on. IEEE, 2006:71-74.
2.2 行列分离压缩感知方法

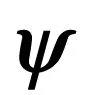

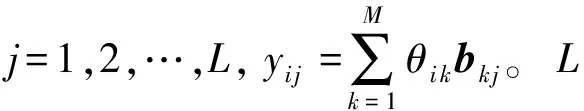

3 行列分离压缩感知的FPGA实现
3.1 行列分离压缩感知FPGA方案框图

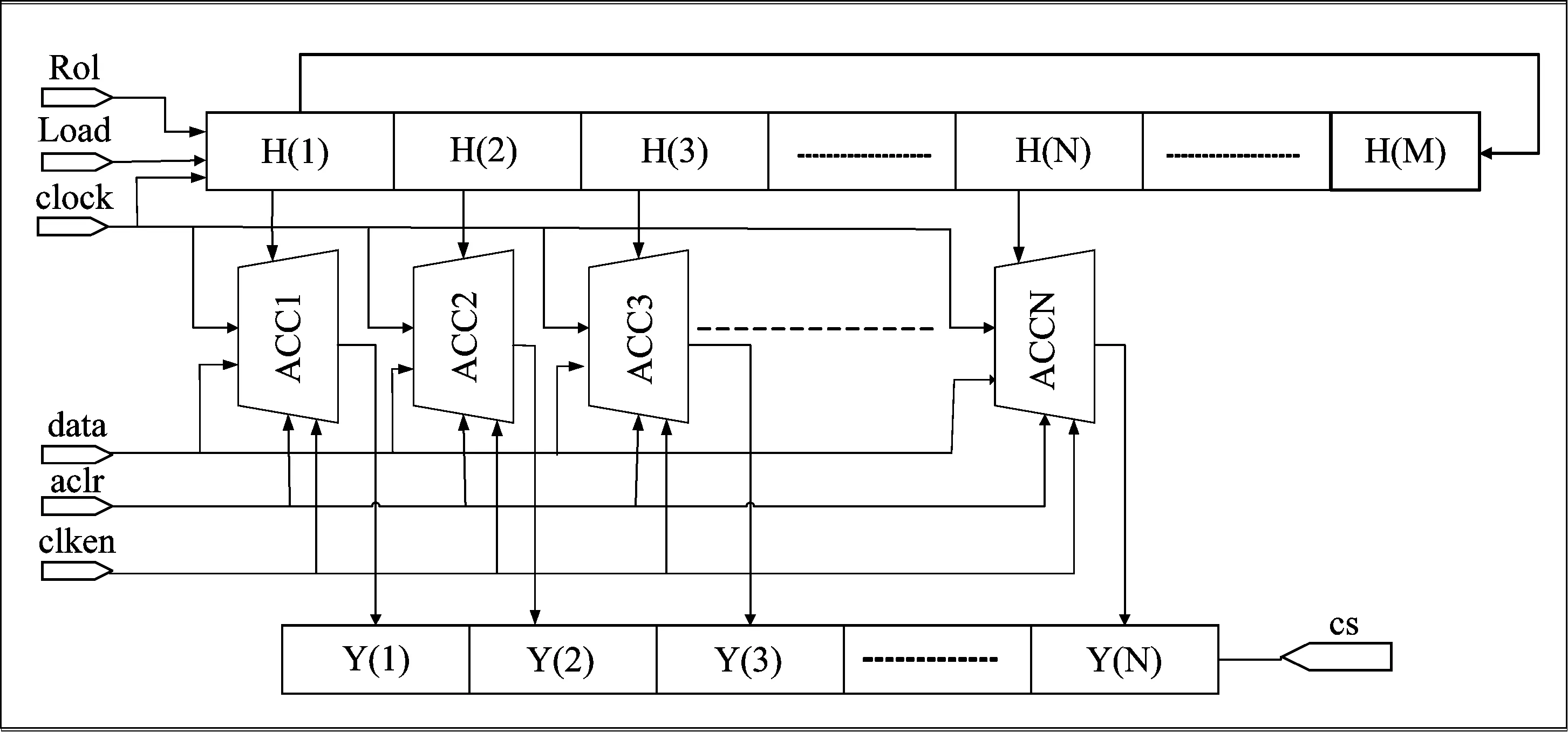
3.2 压缩采样模块
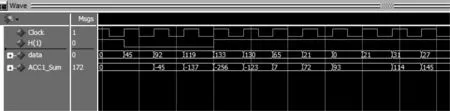
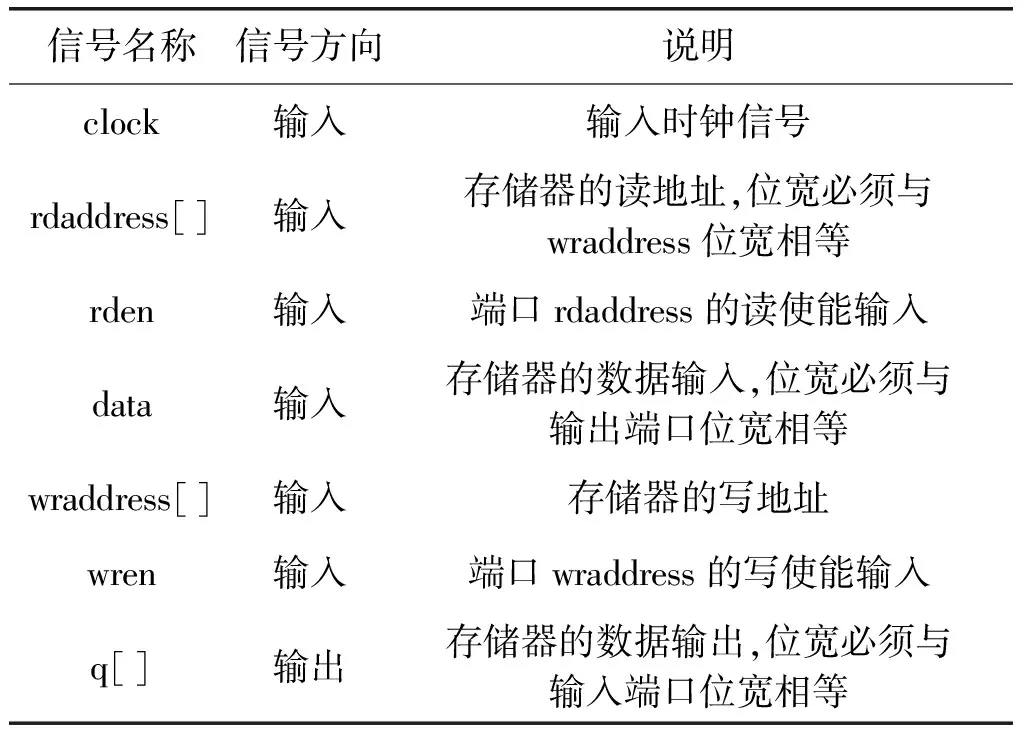
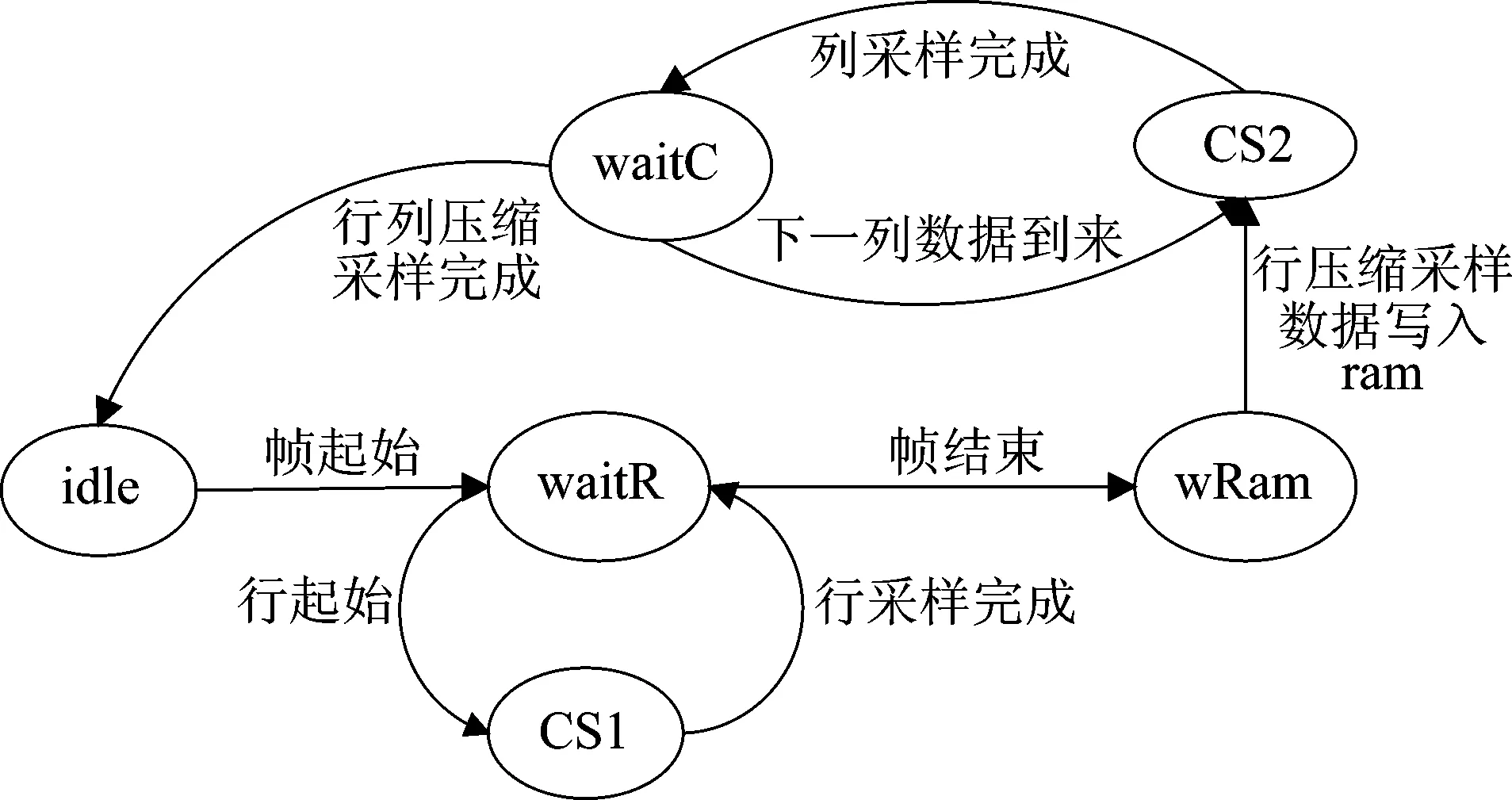
3.3 图像转置存储模块
3.4 控制模块


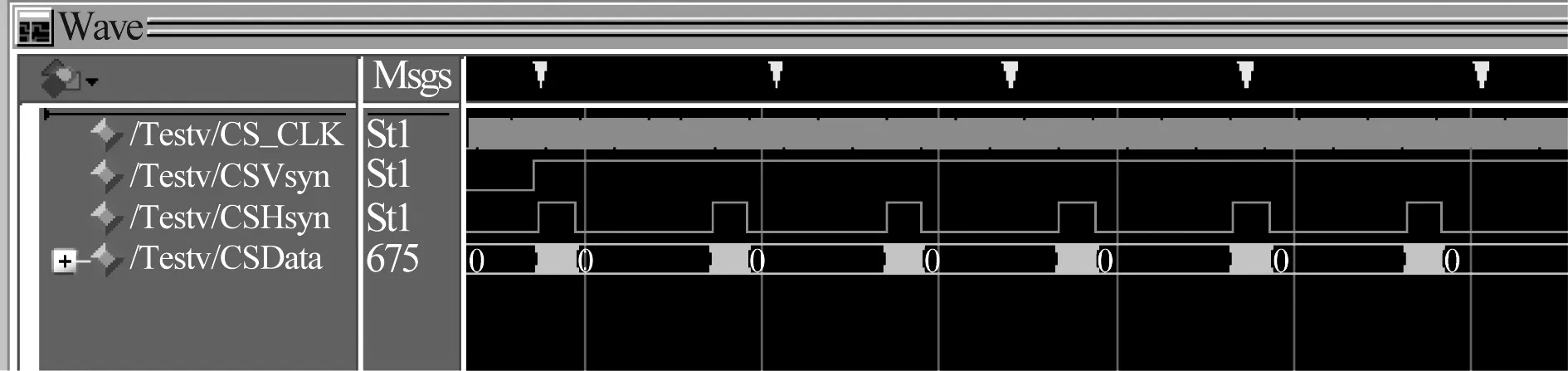
3.5 FPGA电路资源消耗统计
4 仿真实验
4.1 不同压缩率对重构图像质量的影响
4.2 不同类型缺陷的采集和重构


5 结论
