怎样解方案设计题
2018-08-20房延华
文/ 房延华

方案设计问题是中考的重要题型.它以生活中的素材为背景,考查我们运用数学知识解决实际问题的能力.下面以中考题为例,把方案设计题的解法归类总结如下.
一、图形设计问题
例1三块正方形纸板的边长都是60cm,请分别按下列要求设计一种剪裁方法,折叠成一个礼品包装盒(纸板的厚度忽略不计).要求尽可能多地利用纸板,用虚线表示你的设计方案,并把剪裁线用实线标出.
(1)包装礼盒的六个面由六个矩形组成(如图1),请画出设计图;
(2)包装礼盒的上盖由四个全等的等腰直角三角形组成(如图2),请画出设计图;
(3)包装礼盒的上盖是双层的,由四个全等的矩形组成(如图3),请画出设计图.
解:答案不唯一.如图4所示.
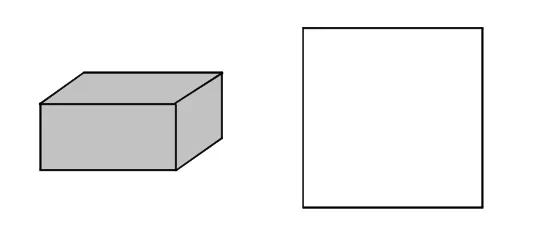
图1
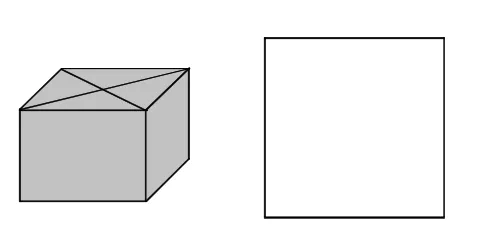
图2

图3
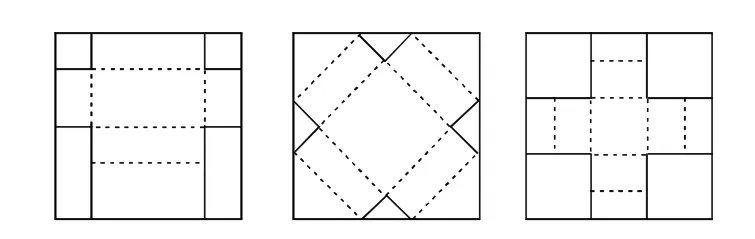
图4
例2阅读以下材料,并按要求完成相应的任务.
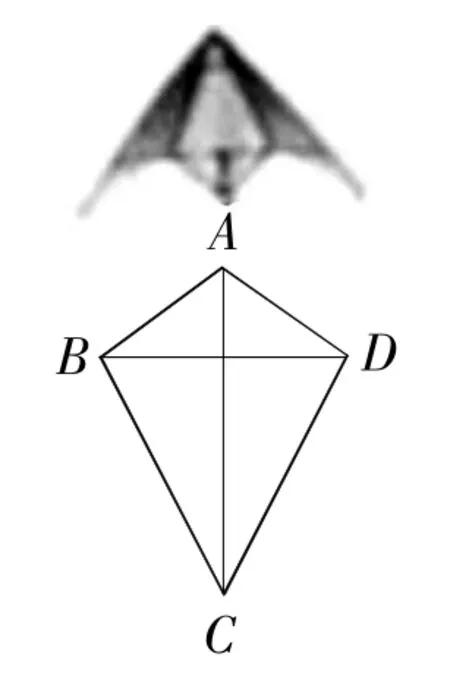
图5
平行四边形、矩形、菱形、正方形和等腰梯形都是特殊的四边形,大家对于它们的性质都非常熟悉.生活中还有一种特殊的四边形——筝形.它的形状与风筝的骨架相似.
定义:两组邻边分别相等的四边形,称之为筝形,如图5,四边形ABCD是筝形,其中AB=AD,CB=CD.
判定:①两组邻边分别相等的四边形是筝形;
②有一条对角线垂直平分另一条对角线的四边形是筝形.
显然,菱形是特殊的筝形,就一般筝形而言,它与菱形有许多相同点和不同点.
如果只研究一般的筝形(不包括菱形),请根据以上材料完成下列任务:
(1)请说出筝形和菱形的相同点和不同点各两条;
(2)请仿照图5的画法,在图6所示的8×8网格中重新设计一个由四个全等的筝形和四个全等的菱形组成的新图案.具体要求如下:

图6
①顶点都在格点上;
②既是轴对称图形又是中心对称图形;
③将新图案中的四个筝形都涂上阴影(建议用一系列平行斜线表示阴影).
解:(1)相同点:①两组邻边分别相等;②有一组对角相等;③一条对角线垂直平分另一条对角
线;④一条对角线平分一组对角;⑤都是轴对称图形;⑥面积等于对角线乘积的一半.
不同点:①菱形的对角线互相平分,筝形的对角线不互相平分;②菱形的四边都相等,筝形只有两组邻边分别相等;③菱形的两组对边分别平行,筝形的对边不平行;④菱形的两组对角分别相等,筝形只有一组对角相等;⑤菱形的邻角互补,筝形的邻角不互补;⑥菱形既是轴对称图形,又是中心对称图形,筝形是轴对称图形,不是中心对称图形.
(2)如图所示:

图7
二、利用方程或不等式设计方案
例3足球比赛规定:胜一场得3分,平一场得1分,负一场得0分.某足球队共进行了6场比赛,得了12分,该队获胜的场数可能是( )
A.1或2. B.2或3. C.3或4. D.4或5.
解:设该队胜x场,平y场,则负(6-x-y)场,
根据题意,得3x+y=12,∵x,y均为非负整数,且x+y≤6,
∴ 当y=0时,x=4;当y=3时,x=3. 选C.
例4某中学计划购进甲、乙两种规格的书柜,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.请解答:
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
解:(1)设甲种书柜单价为x元,乙种书柜的单价为y元.
答:设甲种书柜单价为180元,乙种书柜的单价为240元.
(2)设甲种书柜购买m个,则乙种书柜购买(20-m)个.
∵m取整数,∴m为8,9,10.
购买方案有三种:甲种书柜8个,乙种书柜12个;甲种书柜9个,乙种书柜11个;甲种书柜1个,乙种书柜10个.
三、利用函数设计方案
例5江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)求每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
解:(1)设每台大型收割机1小时收割小麦x公顷,每台小型收割机1小时收割小麦y公顷.
(2)设大型收割机有m台,总费用为w元,则小型收割机有(10-m)台.
根据题意得w=300×2m+200×2(10-m)=200m+4000.

∴有3种方案.
∵w=200m+4000,200>0,∴w随m值的增大而增大,
∴当m=5时,总费用取最小值,最小值费用为5000元.
