基于长短期记忆网络的轴承故障识别

2018-08-20何荇兮张家悦尹爱军

汽车工程学报 2018年4期

唐赛，何荇兮，张家悦，尹爱军

（重庆大学机械传动国家重点实验室，重庆 400044）

随着现代机械制造业的效率提高，在生产过程中，一旦机械设备发生故障就会带来巨大的损失。因此，有效的机械设备故障检测方法具有重大意义。滚动轴承是汽车工业中常用的部件，也是最容易损坏的零件之一，其性能直接影响着汽车的可靠性。杨宇等[1]针对汽车变速器轴承振动信号的非平稳特征，提出了一种基于经验模态分解和自回归模型的滚动轴承故障诊断方法，可以有效识别变速器轴承的工作状态。张红兵等[2]针对汽车滚动轴承系统产生的非线性振动信号的特点，提出用关联维数来描述轴承振动信号的工作状态，进而对其进行故障诊断的方法。

除了传统的轴承故障诊断方法，使用人工智能算法对轴承振动信号进行故障识别逐渐成为研究热点。此类识别方法主要包括特征提取和故障分类两个步骤。国内，贺岩松等[3]利用小波变换的自适应时频局部化优势和奇异值分解，对时频空间特征模式的提取功能提出用小波奇异熵和自组织特征映射神经网络相结合的方法。徐涛等[4]利用谐波小波包分解的归一化特征能量，设计了基于二叉树的多类SVM模型，实现了滚动轴承的故障诊断。尹爱军等[5]提取振动信号在时域、频域、小波域上的38个原始特征，经过等距映射与深度置信网络相结合的算法实现了滚动轴承的故障分类。汤宝平等[6]对故障信号进行经验模态分解，再对表征故障调制特征的本征模态函数计算瞬时幅值欧式范数构成特征矢量，将特征矢量输入到训练好的Elman神经网络中进行故障诊断。王丽华等[7]提出了基于短时傅里叶变换和卷积神经网络的电机故障诊断方法。

汤芳等[8]提出了一种基于稀疏自编码的深度神经网络，实现非监督学习自动提取滚动轴承振动信号的内在特征用于滚动轴承故障诊断。深度学习模型是一种拥有多个非线性映射层级的深度神经网络模型，能够对输入信号逐层抽象并提取特征，挖掘出更深层次的潜在规律[9]。针对传统轴承故障检测存在的采样数据量大、故障特征依赖主观选取等问题，本文提出了一种基于长短期记忆网络的轴承故障识别方法，无需人为提取故障特征向量，直接学习原始的振动信号，实现了故障识别的智能化。王鑫等[10]提出了一种基于长短期记忆循环神经网络的故障时间序列预测方法，同样无需提取预特征，验证了该算法的可行性。

本文首先介绍长短期记忆网络的结构，建立长短期记忆网络的故障识别模型，通过试验得到模型的预测精度，然后提取振动信号小波包能量特征并将该特征输入长短期记忆网络模型和支持向量机模型，试验结果证明，直接运用长短期记忆网络的模型预测正确率更高。

1 基于LSTM的轴承故障识别模型

1.1 LSTM理论

循环神经网络（Recurrent Neural Networks，RNN）是专门用于处理序列数据的深度学习模型。在传统人工神经网络的基础上加入了“记忆”的成分，对当前时刻状态的计算不仅与当前的输入有关，还依赖于上一时刻的计算结果。然而由于“循环”结构的存在，RNN在处理长序列模型时容易陷入梯度消失或梯度爆炸问题。为了解决RNN中的长期依赖问题，Schmidhuber等提出了长短期记忆网络（Long Short Term Memory Networks， LSTM）。如图 1所示，与普通RNN相比，LSTM引入了三个门控制器：输入门（input gate）、遗忘门（forget gate）和输出门（output gate）。门控制器描述了信息能够通过的比例。对于标准循环神经网络，每个时刻的隐层状态由当前时刻的输入与之前的隐层状态相结合组成。但由于记忆单元的容量有限，早期的记忆会呈指数级衰减。为了解决这一问题，LSTM模型在原有的短期记忆单元ht的基础上，增加一个记忆单元Ct来保持长期记忆。

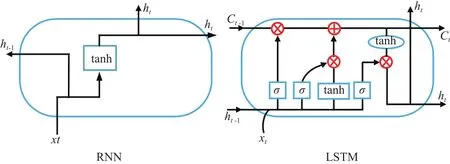
图 1 LSTM对于RNN的改进（多了三个门控制器和一个记忆单元Ct）

1.1.1 临时记忆单元的产生

如式（1）所示，在新的记忆单元Ct产生之前，会先产生临时的记忆单元c'，由这一时刻t的输入层神经元、上一时刻t-1的隐层单元分别与各自权重矩阵的线性组合，跟随非线性激活函数tanh()，得到这一时刻t的临时记忆单元输出c't。

1.1.2 输入门

在产生记忆单元C之前有一个输入门，其作用是判断临时记忆单元c'存储的记忆信息的重要性。如式（2）所示，根据输入层和上一个隐层单元共同判断当前产生的临时记忆单元是否保留，从而判断它以何种程度参与生成最终记忆（或者说对新的记忆的约束）。

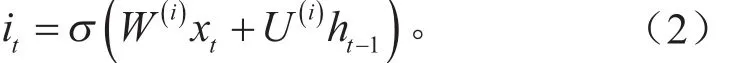
1.1.3 遗忘门

遗忘门与输入门的数学形式相似，它决定了过去记忆单元对当前记忆单元的重要程度，同样的，根据输入神经元和过去的隐层单元来判断过去的记忆单元是否保留。

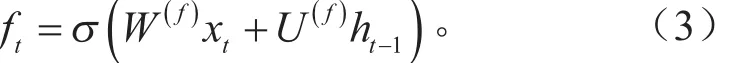
1.1.4 最终记忆单元的产生

如式（4）所示，当前时刻t的最终记忆单元Ct的产生，依赖于通过遗忘门ft控制的过去时刻t-1的记忆单元Ct-1和通过输入门it控制的临时记忆单元c't，将这两者的输出结果相加，得到最终的记忆单元。

1.1.5 输出门

输出门的作用是区分记忆单元和隐层单元，在记忆单元Ct中，存储了大量信息，不仅有临时记忆单元中的短期记忆，还包括过去记忆单元中的长期记忆，大量的信息存在着冗余，记忆单元的信息全部流入隐层作为最后的输出结果会影响模型的性能。输出门的数学形式与输入门、遗忘门类似，如式（5）所示，记忆单元通过一个非线性函数tanh()，再经过输出门的信息筛选，用于隐层单元的迭代，如式（6）所示。

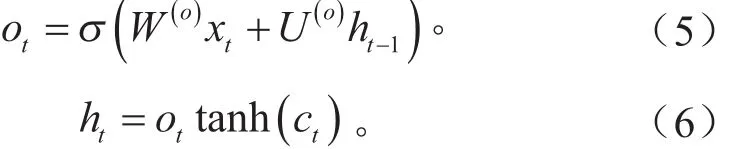
将待处理的训练数据输入到LSTM网络，通过如上逻辑架构的前向计算，就得到LSTM网络的输出，即隐层单元h∈RDh，Dh表示隐层中神经元的数目。对于分类问题，可以映射到一个权重矩阵为W(s)的线性输出层，再跟随softmax函数，计算出分类类别的概率分布。然后按式（8）计算LSTM网络的代价函数。

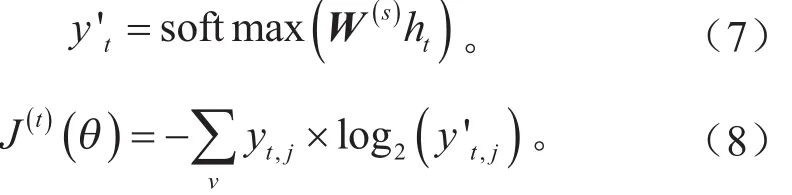
式中：v代表分类数量；yt,j表示在时刻t下属于第j类的真实概率；y't,j表示时刻t下属于第j类的训练概率。

1.2 基于LSTM的轴承故障识别模型

如下描述建立基于LSTM的轴承故障识别模型。

1.2.1 训练阶段

a. 输入层

训练集x∈Rb×t，b表示每次用于训练的小批量样本的个数，t表示样本上的数据维度。引入时间对网络架构的影响，增加时间维度，将训练数据转化为三维矩阵，即Rb×s×i，s代表样本上的时间维度，即序列长度；i代表每一时刻的输入神经元维度。如式（9）所示，将x∈Rb×s×i映射到一个权重为W(i)、偏置为b(i)的线性输入层，改变样本每一时刻的数据维度i。

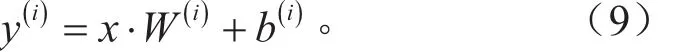
b. LSTM网络层

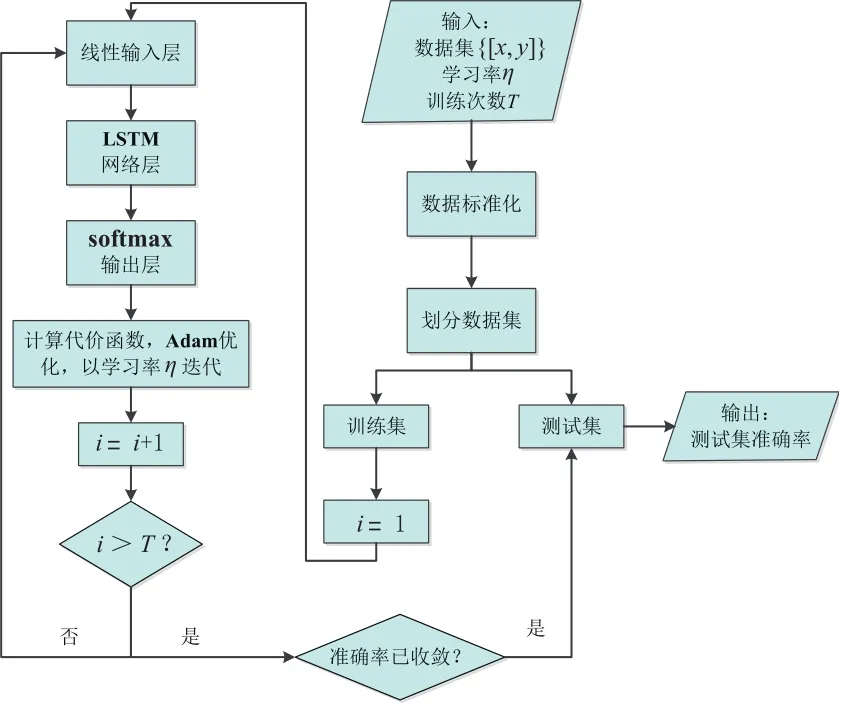
图2 计算流程图

c. 输出层

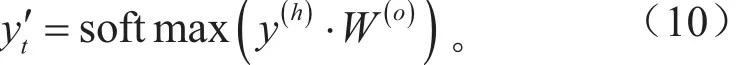
通过softmax输出层，将LSTM网络层的输出维度与最后的分类数目相匹配。式中：W(o)∈Rd×n，n为分类数目。y′∈为网络架构的输出，y′ ∈Rb×n。

d. 代价函数

将训练的输出概率分布与真实的数据分布对比，计算预测输出与实际输出的交叉熵代价函数。

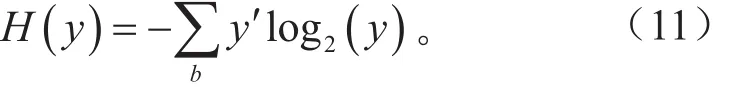
建立如上基于LSTM的网络架构，初始化网络参数，设定训练次数T。每一次训练中，经过前向计算得到当前训练阶段的代价函数，通过误差反向传播进行网络参数的更新，直至达成T次训练，代价函数收敛。

1.2.2 测试阶段

在测试集上，根据训练更新的网络参数来计算预测的分类结果输出，并与真实的类别作比较，计算测试集上的分类预测正确率。

2 试验与分析

2.1 试验数据

本文使用美国Case Western Reserve University电气工程实验室的滚动轴承故障模拟试验台的故障轴承试验数据[14]。试验装置包括电机、转矩传感器、功率计和电子控制设备，如图3所示。使用电火花技术分别在SKF6205轴承的内圈、外圈和滚动体表面加工出0.18 mm，0.36 mm，0.53 mm直径的单点损伤故障。电机风扇端和驱动端故障轴承的振动信号以12 kHz和48 kHz两种不同的采样频率采集得到。图4为四种故障状态振动信号的时域波形比较（采样频率48 kHz，损伤程度0.18 mm，均截取前0.25 s）。可知，内圈失效、外圈失效和正常情况的振动信号有明显差别，滚动体失效与正常情况无明显差别，为直接作用于时间序列振动信号的LSTM模型提供了理论依据。

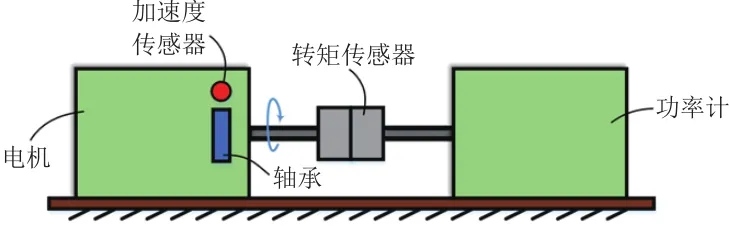
图 3 轴承故障试验平台装置

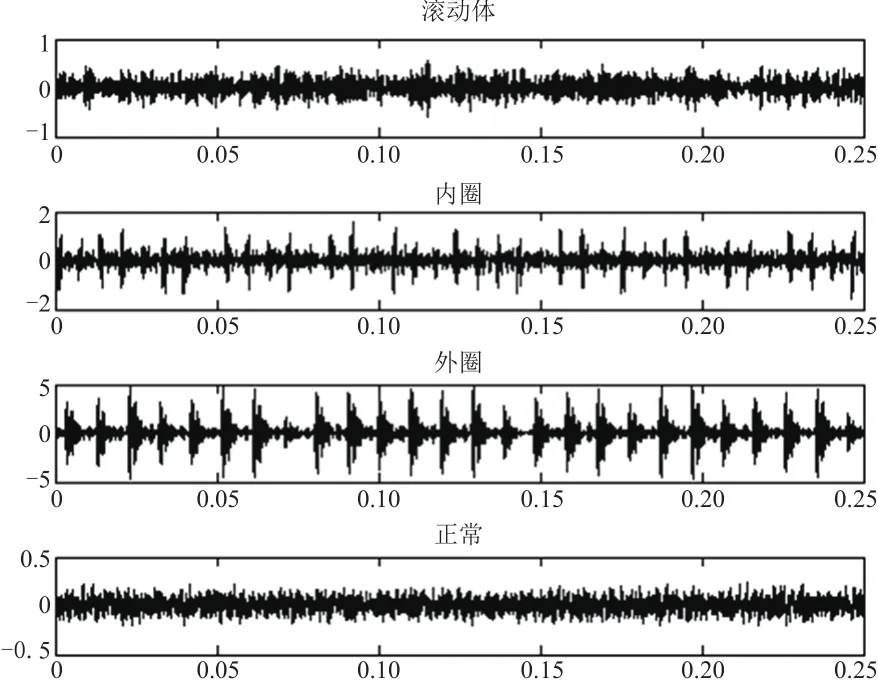
图 4 不同故障部位的时域波形比较

2.2 模型参数对效果的影响分析

尝试先对驱动端轴承下的10个数据集进行分析，载荷为2.205 kW，信号采集频率48 kHz。每个数据集的信号长度为480 000，每2 000个信号组成一个样本，在10个数据集上产生2 400个样本。为了便于训练长短期记忆网络，对每段样本X做标准化处理，如式（12）所示，将样本的向量空间按比例缩放在标准正态分布空间，同时不影响数据自身的分布性质。

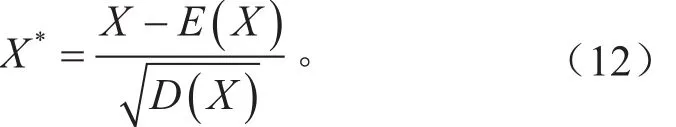
对数据进行预处理后，将2 400个样本按照1∶2的比例随机划分为测试集和训练集。数据集描述见表1。数据集的分类标记基于不同的故障部位和故障尺寸。试验目的是通过学习训练集，寻找数据与分类标记的内在联系，预测测试集上故障轴承的故障部位和故障尺寸。

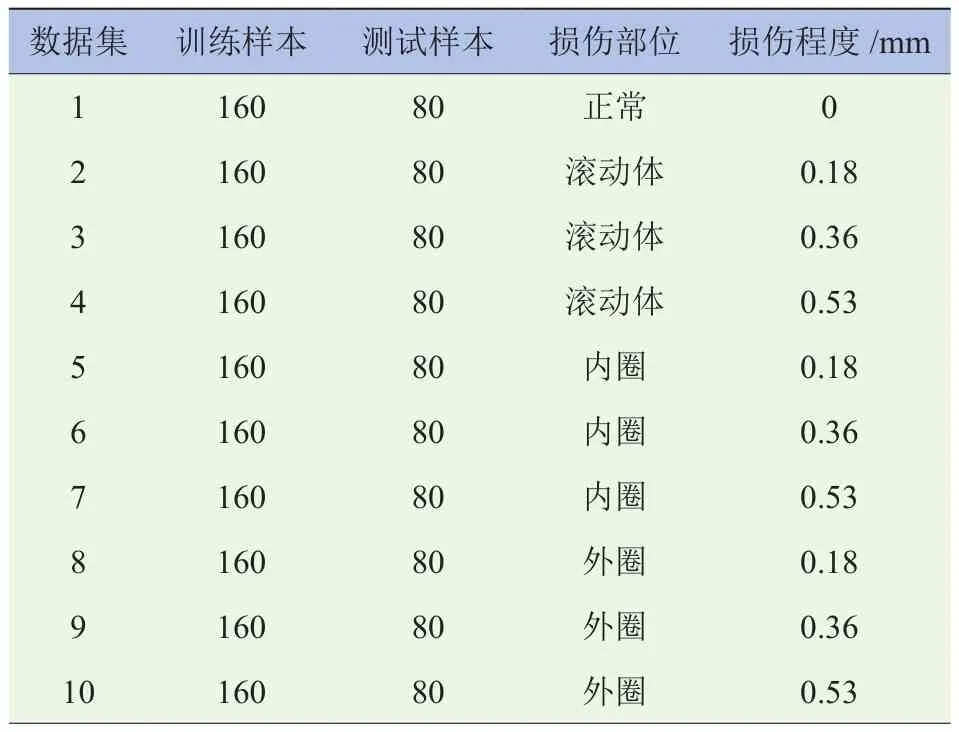
表1 试验数据集

根据建立的基于LSTM的轴承故障识别模型，对该数据进行建模。在训练过程中，一些参数需要自行设定，经过不断迭代，才能得到适合数据的值。对模型性能影响较大的参数有训练次数T、学习率η，序列长度step。试验中尝试对这些参数进行调节。

图5为训练集上的正确率随训练次数T的变化曲线，当训练到2 000次左右，正确率开始收敛，训练到9 000次时，正确率趋势表现为显著下降，随后迅速上升，达到16 800次左右，又小幅下降。预测正确率9 000次后，正确率显著下降，是由于过多的训练次数导致的梯度爆炸，使LSTM单元的神经元激活为0，训练停滞，之后网络重新训练。所以，将训练次数调整为8 000次，可以避免梯度爆炸的出现，并减少运行时间。

图6为不同学习率下正确率随训练次数的变化曲线。学习率为0.001，0.003，0.006时，正确率在迭代次数小于5 000时大致相同，迭代次数为7 000且学习率为0.006时，正确率曲线出现了明显下降。学习率决定了参数迭代到最优值的速度快慢。越大的学习率每次训练时梯度下降的步长越大，越容易跳过最优解。

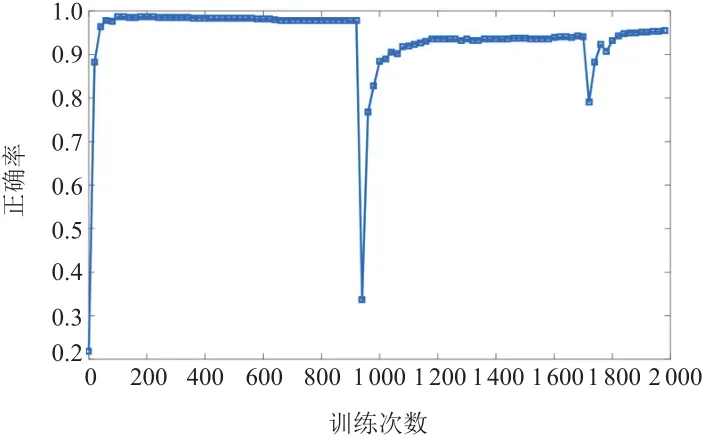
图 5 训练20 000次的正确率变化

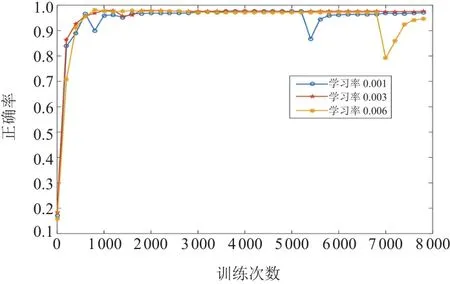
图 6 学习率评估

图7为序列长度s为200和2 000时（学习率0.006，训练8 000次）的正确率变化曲线。LSTM网络中，样本的序列越长，误差向后传播的梯度迭代次数就越多，计算量就越大，影响收敛速度和学习效率。由图7可知，当序列长度为2 000，收敛速度慢，学习效率低，当序列长度为200，正确率则有显著提高，并且也能提升收敛速度和学习效率。

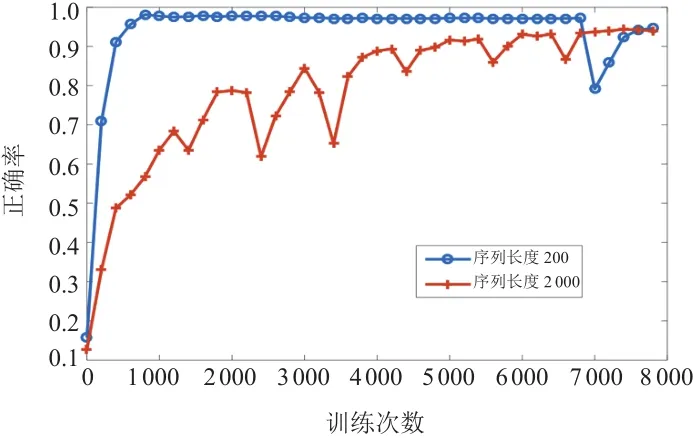
图 7 序列长度的评估

2.3 模型结果

经反复试验和超参数对比，最终确定初始学习率η=0.006，小批量样本大小b=80，序列长度s=200，每一时刻输入神经元个数i=10，LSTM隐层单元的神经元个数d=100，训练次数T=8 000。

该模型正确率最终收敛于98.125%，在10个不同的数据集中，健康状态轴承的预测正确率为100%，其它故障分类的预测结果见表2。

表2 轴承故障分类正确率

2.4 模型对比

为验证模型的正确性，模型结果将与振动信号提取故障特征之后分别使用LSTM模型和支持向量机模型的正确率进行对比。本文提取了小波包能量特征[15]作为模型的输入。

对振动信号选用db10小波进行三层小波包分解，重构第三层8个频带的小波包分解系数，计算对应的归一化的8维小波能量特征向量，并将此能量特征作为LSTM模型的输入。通过试验发现，由于数据规模的减小，运行时间大幅缩短，正确率保持在95.5%，两种模型的正确率变化曲线如图8所示，模型1直接应用LSTM模型，模型2是提取小波包能量特征的LSTM模型，二者比较可得出如下结论：

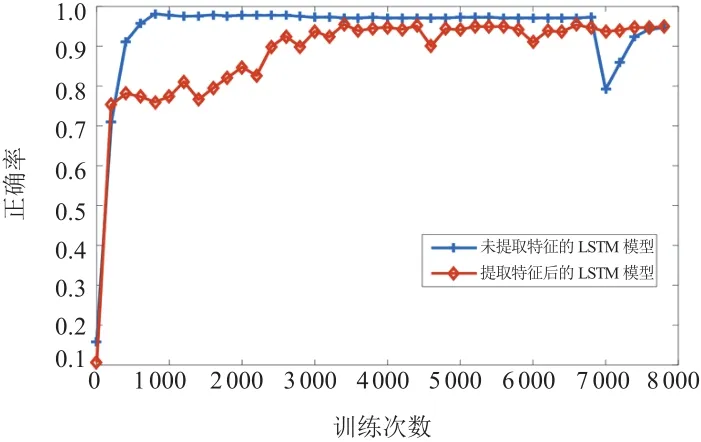
图 8 LSTM模型与提取特征的LSTM模型的比较

（1）直接使用LSTM的每个样本输入维度为200×10，而在时域上提取特征后输入维数降低，正确率也较低。

（2）LSTM主要解决在时序上长期依赖的问题，而相对小波包能量特征是在时序上进一步提取的特征，相互依赖性没有原生数据强。

将小波包能量特征的8维向量作为支持向量机模型的输入。试验中，同样如式（7）所示，先进行数据标准化，在相同的训练集上，通过核函数将低维特征数据映射到高维空间，使用“one-vs-rest”的多分类支持向量机模型训练，核函数选择高斯核，核函数系数设置为0.1，惩罚系数C=1.0，最后相同的测试集得到77%的正确率，低于使用LSTM的分类正确率。

对比基于传统人工提取特征的模型，本文中基于LSTM模型的轴承故障识别模型具有更高的预测准确率。除此之外，基于LSTM模型的方法，无需对特征进行提取和筛选，降低了训练的难度，同时避免了特征选取不当导致的预测精度低下的问题。