斜流环境下导流罩倾覆水动力数值预报研究

2018-08-19王化明赵春慧

浙江海洋大学学报(自然科学版) 2018年3期

盛学，王化明,2，陈林，赵春慧

（1.浙江海洋大学船舶与机电工程学院，浙江舟山 316022；2.浙江省近海海洋工程技术重点实验室，浙江舟山 316022；3.浙江海洋大学东海科学技术学院，浙江舟山 316000）

随着石油、煤矿等不可再生能源的持续消耗，绿色可再生能源的开发已成为人类关注重点。潮流能作为一种绿色可再生能源，具有能量密度高、可预测性强、蕴藏量丰富等优点，越来越受到世界各国青睐。据《中国沿海农村海洋能资源区划》统计，我国沿岸130个水道的理论平均功率约为1.4×107kW，其中浙江、福建、山东和台湾海峡是世界上潮流能资源最丰富的地区之一[1]。但由于潮流流速随太阳、月亮与地球三者之间位置的不同而不停的变化，造成流速很长一段时间处于较低水平，大大限制了潮流能发电装置的能量利用率[2]。

1998年，阿根廷的ISEP小组[3]作出可行性研究，提出了一种对潮流能水轮机性能有很大帮助的改进，即加装导流罩，它能使潮流能量集中起来，使转子附近水域流速增大，从而增大水轮机输出功率，提高效率。2006年，阿根廷布宜诺斯艾利斯大学和美国伊利诺伊大学的PONTA,et al[4]研究低流速环境下浮式潮流能水轮机安装导流罩后的工作状况，实验结果表明低速环境下导流罩能使系统稳定工作，且无需安装齿轮箱等装置，装置利用率大大提升。2008年，加拿大的KHAN,et al[5]在潮流能水轮机实验中对导流罩进一步分析，研究表明导流罩有利于系统聚能效应的提升。而国内早在1989年，张洪雨等[6]就对1 kW直叶片河流发电系统中的导流管进行理论分析和实验论证。2006年，陈晗[7]在弹簧控角竖轴直叶水轮机实验中安装导流罩，研究结果表明安装导流罩后的水轮机性能高于敞水状态下的水轮机性能，但忽略了两种状态下系统稳定性的变化。2009年顾春江[8]从稳定性角度对潮流能水轮机进行优化选型，研究结果表明稳定性是系统优化选型的重要依据，但缺少导流罩稳定性研究内容。2012年崔琳[9]在其学位论文中对座底式水平轴潮流能水轮机的总体设计、流体动力性能与载荷、支撑结构的强度和装置的稳定性关系进行研究，研究表明稳定性是给出导流罩选型的重要前提，但研究环境仅为直流情况。

导流罩作为潮流能水轮机发电系统中重要组成部分之一，研究其性能是当今科学界的一大热门，但目前研究大多集中在导流罩优化选型上[10]，往往忽视其稳定性，且多数研究中潮流方向往往是直流[11-12]，但实际岛屿入海口岸底陡峭、淤泥、暗礁等因素造成潮流方向发生偏移的情况无可避免，且在现实研发中，为了获得高性能导流罩，稳定因素是必须考虑的重要环节之一[8-9]，因此研究斜流环境下导流罩稳定性变化具有极其重要的意义。本文通过粘性流CFD方法对斜流环境下导流罩水动力进行数值模拟，从倾覆性方面进行导流罩稳定性分析，为后续潮流能水轮机发电系统的稳定性计算提供一定参考依据。

1 研究对象

本文导流罩为双向对称结构分布，可适应不同方向潮流，其三维示意图，如图1(a)所示。为更清楚地展示导流罩线型，从图1(b)中可以看出导流罩截面结构，主要包括收缩段、中间段、扩张段，其中收缩段和扩张段型线为维氏曲线型[13]，该线型有利于避免潮流在沿收缩段加速时的边界层分离现象发生，同时保证扩张段出口截面的流线均匀和平行，中间段和外壁型线为直线型。装置各构件主要几何尺寸，见表1。

图1 导流罩基本结构图Fig.1 The basic structure of duct

表1 导流罩主尺度Tab.1 Principal dimensions of duct

2 数值方法

2.1 计算域选择和边界条件的设置

本文导流罩处于无界水域中，计算域入口和侧边界设置为速度入口，顶边界设置为对称壁面，计算域出口设置为压力出口，底边界、导流罩壁面设置为无滑移壁面，如图2所示。

计算域上下游区域距离对导流罩周围粘性流场的分布有重要影响[14]。计算域入口离模型太近，会导致上游区域发生流体阻塞，增大模型阻力。同样地，若计算域出口离水轮机过远，会加大计算运算时间，延长收敛时间[15-16]。为保证计算域内流体能够充分发展，本文计算域上下游距离根据文献[17]进行设置，计算域长度设置为5.00 m，宽设置为4.00 m，高设置为1.03 m，其中导流罩距离入口1.50 m，底边界距离导流罩下表面0.03 m。为方便表述导流罩，本文定义中心线以左区域内导流罩为左侧导流罩，中心线以右区域内导流罩为右侧导流罩，来流方向与中心线的夹角为倾斜角θ，逆时针为旋转正方向，如图3所示。

图2 计算域Fig.2 Computational domain

图3 潮流方向Fig.3 Trend direction

2.2 网格划分和湍流模型

在STAR-CCM+软件中完成建模、网格划分，如图4所示。对导流罩周围进行网格加密，并在近壁面区域设置5层边界层网格，以保证导流罩周围流场的计算精度，网格增长率设置为1.5，最小边界层网格距离导流罩壁面距离为3.1×10-5m，整体网格数量为1.31×106，如图4(b)所示。

图4 导流罩周围网格Fig.4 Computational grid around duct

在本文中流体为淡水，常温常压下设为不可压缩流体，密度ρ=998.2 kg/m3，动力黏度μ=1.003×10-3Pa·s。来流速度Vmin=0.1 m/s，导流罩特征尺寸L=1.00 m，最小雷诺数为9.853×104，满足湍流流动条件。

研究采用RANS方法进行数值模拟[18-20]，湍流模型选用realizable two-layer k-ε湍流模型，运用分离流求解器，压力与力矩耦合采用SIMPLE算法，其中压力项的亚松弛因子设定为0.2，其他项的亚松弛因子设定为0.8。

3 流场计算与结果分析

为预报不同斜流环境下导流罩稳定性差异，本文对导流罩周围流场进行数值分析，通过监测倾覆力矩Q，研究不同来流速度V和倾斜角θ对导流罩倾覆水动力的影响。为方便表征导流罩水动力特性，参考文献[11-12]定义以下系数。

yoz平面内倾覆力矩系数：

xoy平面内倾覆力矩系数：

式中：V—导流罩扩张段入口来流速度，m/s；

ρ—流体密度，kg/m3；

d—导流罩中间段宽度，m；

l—导流罩形心到系统中心的横向长度，m；

Qx—倾覆力矩在yoz平面内的分量，其旋转中心指向x轴正方向的力矩，N·m；

Qz—倾覆力矩在xoy平面内的分量，其旋转中心指向z轴正方向的力矩，N·m。

从图5和图6可以看出，当V=0.4 m/s，倾斜角θ=45°时导流罩周围流场的速度分布云图和压力分布云图。可以清楚地看到即使在斜流环境下，导流罩内部流场部分区域的速度大于外部流场，导流罩仍起到一定的聚流效果，但内部压力和单侧导流罩壁面压力明显不同。

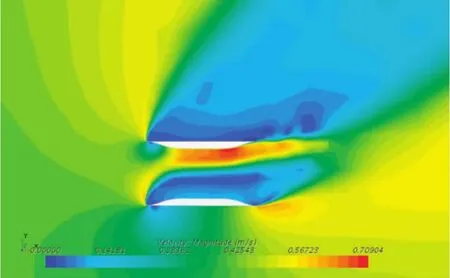
图5 θ=45°导流罩周围流场速度分布云图Fig.5 Velocity distribution around the ducts at θ=45°

图6 θ=45°导流罩周围流场压力分布云图Fig.6 Pressure distribution around the ducts at θ=45°

针对不同斜流情况，研究采用不同来流速度V，依次选取0.1 m/s，0.4 m/s，1.0 m/s，2.0 m/s，对应每一组流速，倾斜角 θ分别选取 0°、15°、30°、45°、60°、75°、90°，共 28 种工况，见表 2。

表2 工况情况表Tab.2 Results for cases with different condition

从图7可以看出倾斜角θ、来流速度V与左侧导流罩倾覆力矩系数CQ关系曲线图。从图中可清楚看出，不同斜流情况，导流罩倾覆力矩系数差异明显。观察图7(a)可以发现，yoz平面内，当 θ=0°时，左侧导流罩CQx曲线位于正向最大值处，且V越大，CQx越大；θ在[0°，15°]范围内，随 θ增大，CQx曲线递减，且斜率最大；从数值上分析，θ在[15°，90°]范围内，CQx整体偏小。

图7 斜流环境下左侧导流罩倾覆力矩系数曲线图Fig.7 Overturning moment coefficient curve of the duct at left side under inclined flow

从图 7(b)可以看出，xoy 平面内，θ在[0°，90°]范围内，CQx始终保持小于 0；θ在[0°，45°]范围内，随 θ增大，CQx曲线递减，但从数值上分析CQx越来越大，当θ=45°时，CQx最大，此时左侧导流罩倾覆趋势最为明显，稳定性最差；θ在[45°，90°]范围内，CQx曲线递增，但从数值上分析 CQx越来越小，θ在[60°，90°]范围内，CQx几乎等于0。

从图8可以看出，V=0.4 m/s时，斜流环境下左侧导流罩内外壁面压力分布云图。可以清楚地看出，斜流环境下左侧导流罩内外壁面压力分布趋势变化明显不同，外壁面压力分布相对单一，较均匀，且整体偏小，内壁面压力分布区别较大，θ在[0°，45°]范围内，内壁面入口段压力明显大于出口段，推动导流罩顺时针旋转，蕴含倾覆倾向，当θ=45°时内壁面出入口段压力相对差值最大，此时倾覆最显著，印证了图7中结论。

导流罩利用内壁型线对来流进行干扰，使潮流汇聚于内部，当来流方向发生改变时，造成斜流环境，使单侧导流罩分别处于上下两游，左侧导流罩位于下游，内壁面先于外壁面接触变化潮流，使内壁面压力偏大，分布趋势变化更直观。

从图9可以看出，倾斜角θ、来流速度V与右侧导流罩倾覆力矩系数CQ关系曲线图。从图9(a)可以看出，yoz平面内，θ在[0°，90°]范围内，右侧导流罩CQx始终小于0，随θ增大，CQx曲线递减，但从数值上分析CQx逐渐增大，θ=90 °时，CQx最大，且整体大于其他工况情况，倾覆趋向最为明显，蕴含较大安全隐患；对比不同V情况可以发现，V越大，CQx数值越大，在[0°，15°]范围内尤为明显。

从图9(b)可以看出，xoy平面内，当 θ=0°时，CQx大于 0，随 θ增大，CQx急剧减小；θ在 [5°，90°]范围内，CQx保持小于0，从数值上分析，θ=15°时，CQx最大，此时右侧导流罩倾覆趋势明显，稳定性较差。

图8 V=0.4 m/s斜流环境下左侧导流罩内外壁面压力分布云图Fig.8 Pressure contour of inside wall and outside wall of the duct at left side under inclined flow at V=0.4 m/s

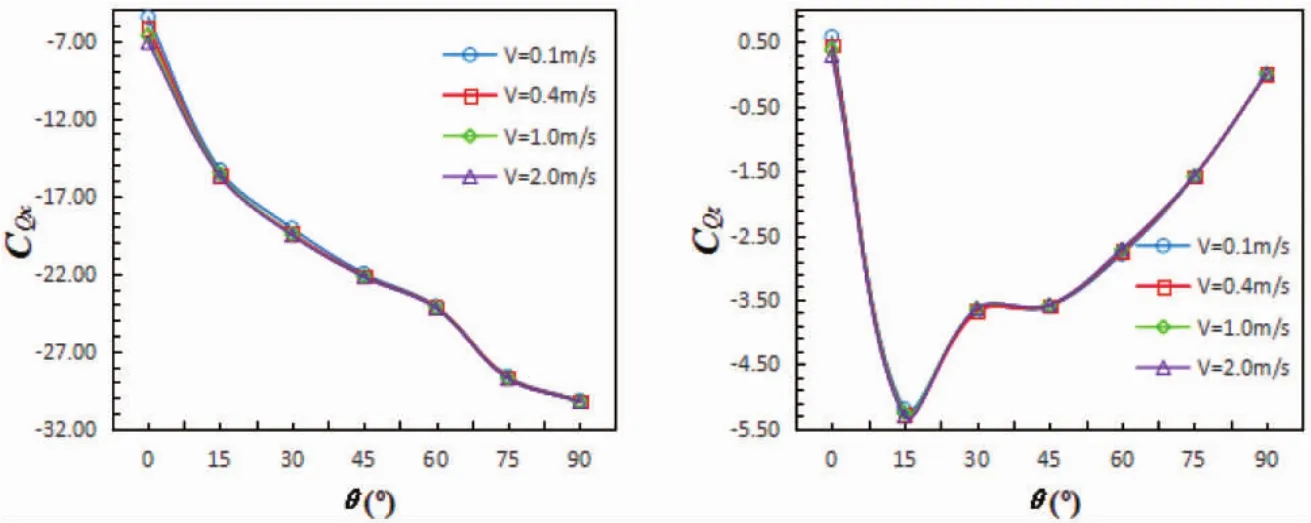
图9 斜流环境下右侧导流罩倾覆力矩系数曲线图Fig.9 Overturning moment coefficient of the duct at right side under inclined flow

从图10可以看出，V=0.4 m/s时，斜流环境下右侧导流罩内外壁面压力分布云图。可以清楚地看到，斜流环境下右侧导流罩内壁面入口段压力小，出口段压力大，存在顺时针旋转倾覆趋向，θ=15°时内壁面出入口段压力相对差值最大，此时顺时针旋转倾覆最显著；θ在[0°，90°]范围内，外壁面压力整体偏大，出入口段压力差异明显，随θ增大，高压区域逐渐向中间段靠拢，因导流罩为座底安装，使导流罩向内翻倒趋势显著，θ=90°处最明显，此时稳定性最差，印证了图9中结论。

在斜流环境中，右侧导流罩处于上游区域，直接受潮流影响，当倾斜角度超过一定值后，潮流直接冲击外壁面，使外壁面压力变大，加剧倾覆趋势，危害装置稳定性。