基于微桩复合模量和复合地基的闸室结构分析
2018-08-18曹睿哲
曹睿哲
(上海市水利工程设计研究院有限公司,上海市 200064)
0 引言
随着水利事业的发展,由于地形、地质条件的限制,许多水工建筑物不得不建设在软土地基上[1]。但是软土地基往往不能满足上部结构对地基承载力和沉降的要求,为了提高地基的承载力和降低水工建筑物的沉降,工程界采取不同的措施对地基进行了处理[2]。近年来,由于地基处理技术的发展,复合地基在水利工程中得到越来越广泛的应用,其已成为很多地基处理方法的理论分析与公式建立的基础和根据[3]。
在复合地基计算中,复合模量法的应用较多,该方法的关键是复合模量表达式的合理性,其对变形计算结果具有直接的影响,这也是广大工程技术人员关心的重要问题之一。另外考虑到闸室结构的受力变形情况与闸室地基的设计密切相关,是不可分割的统一整体。因此,开展微桩群复合地基复合模量闸室结构分析研究是十分有意义的。
1 计算理论
1.1 法基本原理[4~8]
有限元法是将连续体用网格划分为有限数目个单元体,这些单元体之间在节点处相互铰结,形成离散结构,用这些离散结构来代替原来的连续体结构,以分析应力和变形,将荷载移置作用于离散结构的节点上,成为节点荷载。应力—应变关系表示为:

式中:[D]为弹性矩阵。由虚位移原理和应力—应变关系,可建立节点荷载和节点位移之间的关系,即

式中:[K],[δ],[R]分别为刚度矩阵,节点位移和节点荷载列阵。解方程可求得位移,进而可推出应变[ε]和应力[σ]。
1.2 复合地基复合模量理论分析
复合模量表征的是复合土体抵抗变形的能力。由于复合地基是由土和增强体(桩)组成的,因此,复合模量与土的模量和桩的模量密切相关。目前,复合模量的确定方法主要有以下四种方法。
(1)面积加权法[9]
面积加权法是复合模量的传统求解方法,即在等应变假定的基础上求解复合模量。复合地基复合模量Ecs用面积加权平均法计算,即

式中:Eps为桩体压缩模量;Ess为桩间土压缩模量;m为复合地基置换率。
(2)增大系数法[10]
闫明礼、曲秀莉等推导出了以下方法计算复合模量:
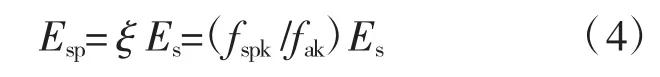
式中:fspk为复合地基的承载力设计值;fak为天然地基承载力特征值;ξ为模量增大倍数。
(3)参变量变分法
郑俊杰、区剑华等在对桩间土采用双折线弹塑性模型分析的前提下,利用参变量最小势能原理对多元复合地基的复合模量进行求解。这种方法考虑到了应力水平变化会引起复合模量的变化。
(4)静荷载试验法[11]
由复合地基荷载试验可以绘制压力p与沉降的关系曲线,即p-s曲线,通过这条曲线可进一步求得复合地基的复合模量E0,计算公式如下:

式中:d为圆形载荷板直径,如为矩形荷载板,则按照面积等效的原则换算得到等效直径;μsp为复合地基泊松比,μsp=mμp+(1-m)μs,μp和 μs分别为桩和桩间土的泊松比。
3 实例分析
3.1 工程概况
某水闸共3孔,中孔净宽7 m,两侧边孔净宽各5 m,胸墙底高程为4.0 m,闸顶、胸墙顶高程均为7.5 m。该工程持力层为软弱地基,因此采用钢筋混凝土30 cm×30 cm的预制方桩来处理地基。桩尖高程为-12.0 m,桩长10.6 m,共285根方桩。底板面层高程为0.0 m,底板厚1.4 m,顺水流方向长15 m,垂直水流方向长21.4 m。
在建立空间三维有限元模型时,地基模型尺寸地选取对计算结果有一定影响[12],为了使计算结果更符合实际,根据萨布尼斯等著的相关国际权威文献中对试验模型尺寸的要求,认为取地基单边尺寸为结构基础单边尺寸的1~5倍就可以反映地基对基础的作用[13]。本次计算的模型在地基的顺水流方向取闸室长度15 m,垂直水流方向取64.2 m,深度取至高程-20 m。
为了提高网格的划分质量,在不影响计算结果的前提下,对所建的模型做了一定的简化处理。模型地基的左右及前后边界为垂直于该面的链杆约束,底面为固接约束。对模型进行网格剖分时,主要采用结构化网格剖分技术。为了更有利于非线性有限元分析,采用六面体减缩线性积分单元,其中闸室和桩体离散为64 562个单元,土体离散为110 522个单元。
由于钢筋混凝土的应变远小于土体的应变,故闸底板及预制方桩采用线弹性材料模拟,土体为弹塑性材料,假定服从Mohr-Coulomb屈服准则[14~16],由于土体自重产生的变形在成桩前已基本完成,故计算中不计入土体自重引起的应变。在底板底面与土体以及桩与桩周土体之间设置了滑动接触面,桩基和底板作为主控接触面,土体作为从属接触面[17],分别模拟底板与土以及桩与土的相互作用,其摩擦系数均取为[18]。底板与桩基的接触近似看做是固接的。闸室结构三维有限元模型见图1。

图1 闸室结构三维有限元模型图
3.2 基本荷载和计算工况
模型施加的荷载主要包括固定荷载、回填土荷载和水荷载。固定荷载主要考虑闸室结构自重。根据《水工建筑物荷载设计规范》(DL5077—1997),墙后水平土压力按主动土压力计算,边荷载按垂直土重计算。按照历年水位变化和现行运行状况,水荷载的加载工况见表1。

表1 计算水位组合表
3.2 计算结果分析
由于实际的工程是微桩群复合地基,故在对该闸进行建模分析时主要考虑两种方法:方法1是根据面积加权法中式(3)计算出相应的复合模量,采用三维有限元进行计算,方法2是建立实际微桩群复合地基进行三维有限元计算。
(1)微桩群复合地基复合模量与沉降分析
按照上述两种方法分别进行有限元计算,计算时均在底板表面加载100 kPa的竖向均布荷载。方法1沉降值分布图见图2。方法2沉降值分布图见图3。
由图2、图3可知:方法1由于采用复合模量法,加固区视作一均质的复合土体,加固区的复合模量远远大于周边土体的变形模量,故加固区的沉降变化较小且把上部荷载均匀地传递给下卧土层,周边土体的沉降变化较大。方法2在加固区由于是桩土共同作用把上部荷载传递给下卧土层,加固区的沉降变化相对方法1来说有所增大,这是由于微桩桩端会刺入下卧土层,产生一定的沉降,此处体现出了两种方法在沉降机理上的差异性。方法1和方法2的最大沉降值分别为 22.78 mm、31.74 mm,误差为 8.96 mm,误差较大。

图2 方法1沉降值分布图(单位:m)

图3 方法2沉降值分布图(单位:m)
(2)微桩群复合地基复合模量参数分析研究
a.荷载的影响
采用两种方法分别进行有限元计算,加载时主要考虑竖向荷载的变化。两种方法计算的最大沉降值曲线以及相应的拟合曲线见图4。
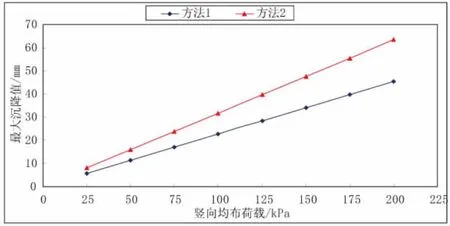
图4 两种方法的最大沉降值曲线图
由图4可知:在一定荷载范围内,随着竖向荷载的变化,两种方法的沉降变化趋势相同且方法1的计算结果均小于方法2,但是随着荷载的增大,两者的误差越大。这是由于在方法2中,微桩的刚度远远大于下卧层土体的刚度,随着上部荷载的增大,微桩刺入下卧土层的现象越明显,所以误差就越大。
b.复合地基桩端下卧土层泊松比的影响
计算时在底板面层加载100 kPa的竖向均布荷载,随着复合地基桩端下卧土层泊松比的变化,两种方法的最大沉降值曲线以及相应的拟合曲线见图5。
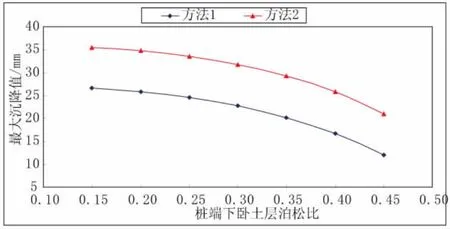
图5 两种方法的最大沉降曲线图
由图5可知:随着复合地基桩端下卧土层泊松比的变化,两种方法的最大沉降值均减小,变化趋势相同,但是方法1的计算结果均小于方法2,两种方法的计算误差基本不随下卧土层泊松比的变化而变化。
c.桩土模量比的影响
计算时在底板面层加载100 kPa的竖向均布荷载,随着复合地基桩土模量比的变化,两种方法的最大沉降值曲线以及相应的拟合曲线见图6。
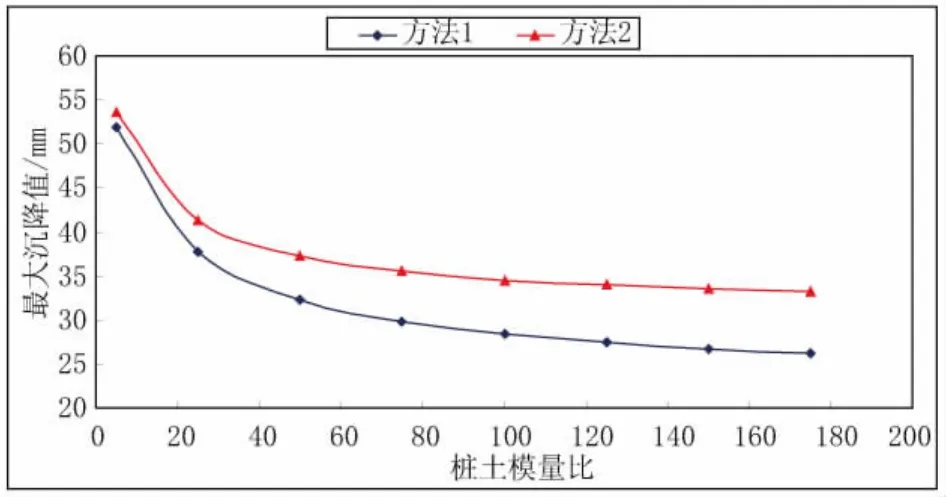
图6 两种方法的最大沉降曲线图
由图6可知:随着桩土模量比的增大,两种方法的最大沉降值均减小且变化趋势相同,在同一桩土模量比下,方法1的最大沉降值均小于方法2的最大沉降值。当桩土模量比小于20时,两种方法计算所得的最大沉降误差较小,当桩土模量比大于20时,两种方法计算所得的最大沉降误差逐渐增大。这是由于当桩基与土体的刚度差越小时,桩基向下卧土层刺入的现象越不明显,两者的误差就越小。由此可见,在一定的桩土模量比范围内,采用方法1计算复合地基沉降时,计算结果是偏小的,并且随着桩土刚度比地增大,误差增大,所以方法1对柔性桩较适用。
(3)微桩群复合地基复合模量与闸室结构分析
a.闸室结构沉降分析
采用方法1和方法2分别对闸室结构进行三维有限元计算分析,根据计算结果,各工况下闸室结构特征位置的沉降值见表2。在正向设计工况下两种方法的闸室结构沉降分布见图7、图8。

表2 闸室结构特征位置的沉降值 mm
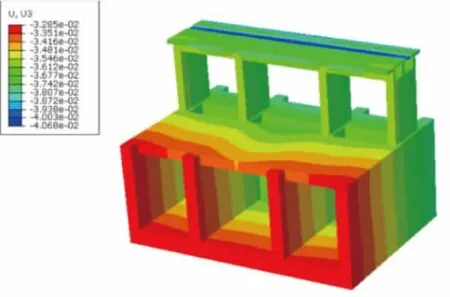
图7 方法1闸室结构沉降分布图(单位:m)

图8 方法2闸室结构沉降分布图(单位:m)
由表2、图7、图8可知:方法1闸室各工况下的沉降较均匀,沉降差较小,与方法2计算的结果相比误差偏大,这是由于方法1计算时,加固层采用复合模量进行计算,加固层的刚度较大,从而沉降值与沉降差均偏小,这与实际的微桩群复合地基在荷载传递机理上是有区别的。因此,对于刚性桩复合地基,采用方法1计算闸室结构的沉降是偏小的。
b.闸室结构应力分析
根据计算结果,方法1和方法2在各工况下闸室结构的最大主拉应力值见表3,最大主压应力值见表4。在正向设计工况下最大主拉应力分布图见图9、图10,最大主压应力分布图见图11、图12。
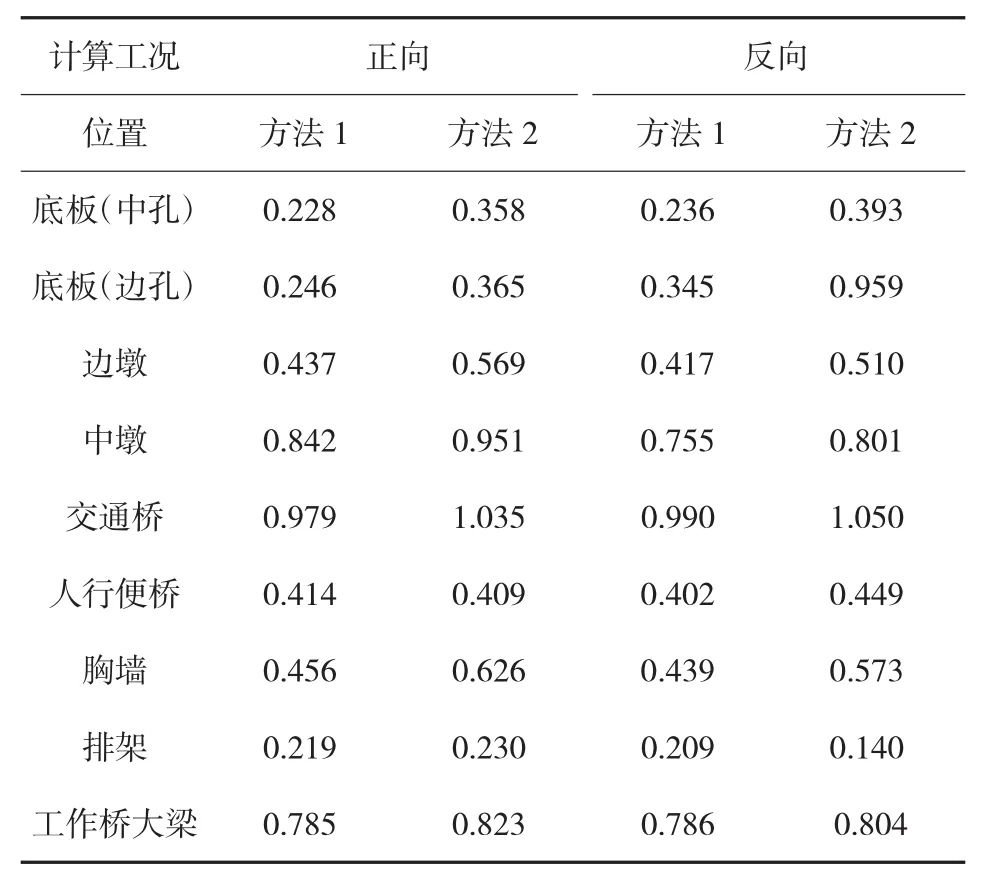
表3 闸室结构的最大主拉应力值 MPa
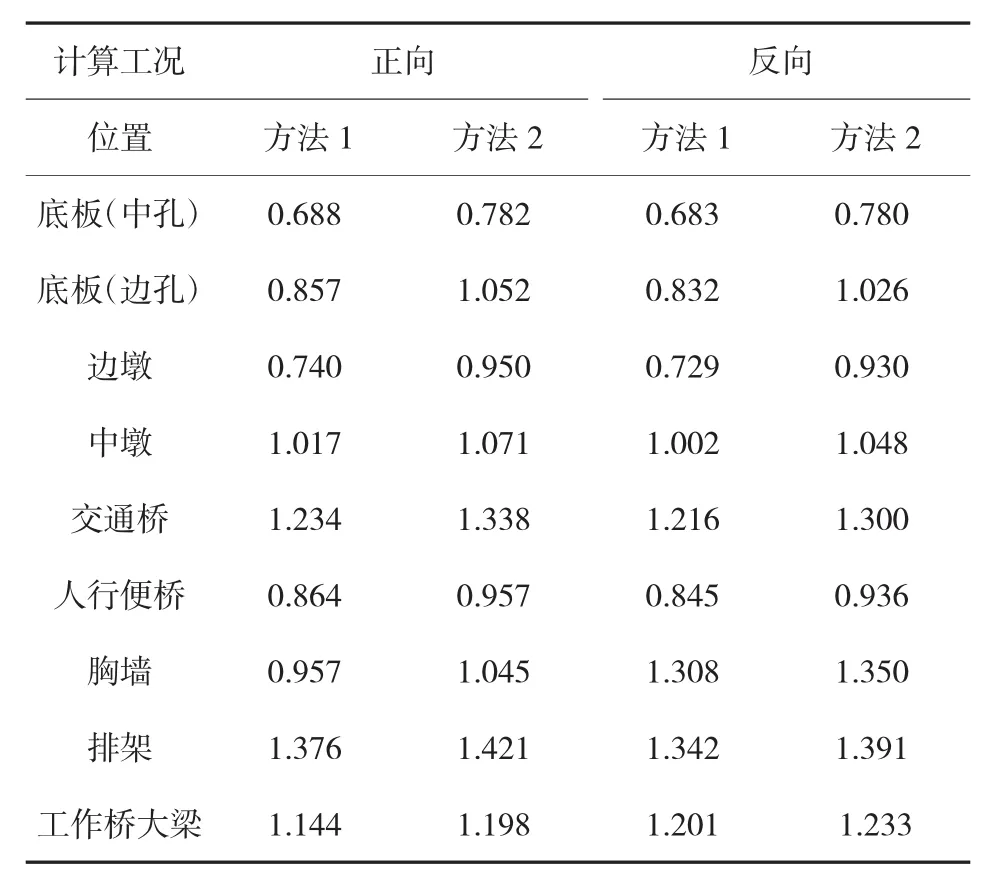
表4 闸室结构的最大主压应力值 MPa
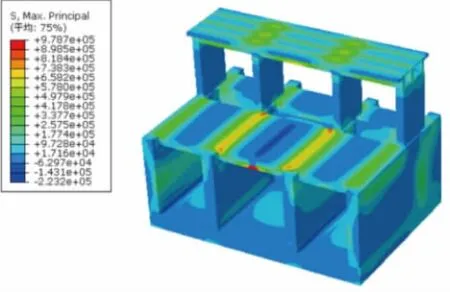
图9 方法1最大主拉应力分布图(单位:Pa)
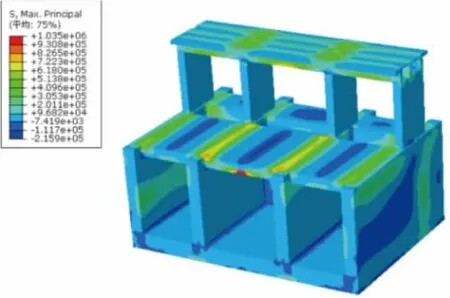
图10 方法2最大主压应力分布图(单位:Pa)
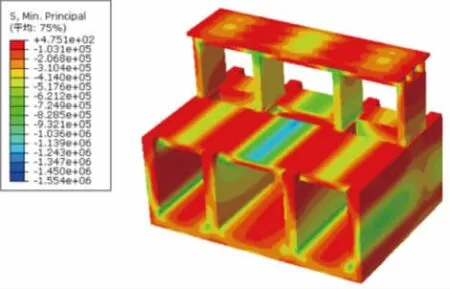
图11 方法1最大主拉应力分布图(单位:Pa)

图12 方法2最大主压应力分布图(单位:Pa)
由表3、表4和图9~图12可知:采用方法1计算闸室结构的应力与采用方法2进行计算的结果相比,两者是存在差异性的,但变化幅度较小。这是由于两种方法在地基的荷载传递机理上是不同的,从而对闸室结构的应力分布的影响也是不同的,计算结果有所差异。由于闸身上、下游的公路桥和人行便桥与闸室底板及闸墩一起浇铸成为三孔一联式的箱型涵洞结构,闸室整体的刚度较大,闸室整体性较好且适用于各种地基条件。因此,各结构的应力值均较小且对地基的荷载传递机理的变化不敏感。
在实际的微桩群复合地基的工程设计中,一般采用方法1来对闸室结构进行计算分析,本文通过两种方法的比较可知方法1对闸室结构强度的计算基本是可行的,对计算结果的影响不大,但对闸室沉降计算的误差较大。对于一些大型工程则不能忽视两种方法的误差,对于误差应给予足够的重视,以此来保证工程设计的可靠性与安全性。对于方法1,关键因素是复合模量的正确选用。
4 结论
(1)对两种方法的沉降计算结果分析可知,两种方法的计算结果是存在较大误差的,因此,对于刚性桩复合地基,在采用复合模量法进行沉降计算时,要合理准确地确定复合模量的大小且对计算结果进行修正。
(2)分别采用两种方法,分析研究了竖向均布荷载、桩端下卧土层泊松比、桩土模量比对微桩群复合地基最大沉降值的影响,从中了解了各参数对最大沉降值的影响规律,同时可以看出方法1较适用于柔性桩,这与规范所规定的适用条件是相吻合的。
(3)采用两种方法对闸室结构的四种工况分别进行有限元计算,经过对比分析可知,方法1的沉降值及沉降差均减小。两种计算方法的闸室结构应力存在差异,但变化幅度较小。采用方法1计算闸室结构内力基本是可行的,对计算结果的影响不大,但对闸室沉降计算的误差较大。对于方法1,关键因素是复合模量的正确选用,因此,在今后除了理论分析研究外,还需要更多的工程实例,积累完整的沉降观测资料,不断对比完善,从而使设计计算更加符合实际。
