合同节水管理项目利益分配方案

杨楠 陈荣 李佳杰

【摘要】合同节水管理项目是一种可以实现多方共赢的节水行为，但是在实现节水效益公平分配方面仍存在一定的问题，阻碍该项目的推广。本文针對我校一实例，采用Shapley算法进行利益的分配，并引入理想点对其分配值进行修正，以提出一种根据多方付出的程度的不同，尽可能公平的利益分配的处理方案。

【关键词】合同节水管理 Shapley算法 理想点

1 背景知识

在党的十九大中，明确提出了关于环保能源的问题、我国人均水资源匮乏，更应该注重水资源的合理利用。

在节水需求的大环境下，合同节水管理项目也便应运而生，合同节水管理项目引入社会化资本，具有广阔的应用前景，然而其利益分配机制不健全导致实施过程中各参与方在分享节水效益的比例上很难达成一致，阻碍了合同节水管理项目的发展。

合同节水管理项目主要应用三种运行模式：节水量保证模式、节水效益分享模式和固定投资回报模式，其中采用较为多的是节水效益分享模式。

节水效益分享模式即节水服务公司通过合同管理的方式募集资本，集成先进适用的节水技术和产品，对用户指定项目进行节水技术改造，建立长效节水管理机制，分享节水效益的新型市场化节水模式。在项目合同运行期间，节水服务公司实际上承担了项目运行和融资两项风险。

2 案例分析

以我校的一合同节水项目为例，此项目采用节水效益分享模式，我校两个校区作为合同节水管理的试点区域，开展相应的实践活动。本文中拟用其中相关数据进行模拟分配计算。

2.1 案例情况

我校节水项目概算990万元，合同期6年，工作历时100天左右。北京GTJS公司对教学楼、学生宿舍、办公楼共计69栋老式耗水洁具进行节水器具更换。并对地下网管及设施进行全面检漏，检出并修复漏点31处，对老旧管道、阀门进行更换，共建地下管网约8000米。还建设用水监管平台，通过安装远传水表283块；监控软件升级改造，建立实时监控平台。在节水改造后，我校在2015年3月到12月，与同期相比累计节水122.2万m3，当地水价以3.98元/m3（假设水价在此期间保持不变），则节约水费486.4万元。

2.2 Shapley算法初始分配

假设N为从事合同节水管理项目的一个组织，其中有n个个体，非空子集S为N中的任意一个联盟，V（S）为通过联盟合作可获得的收益。

设节水服务公司为F，用水客户为Y，主要资金提供者为Z，即北京节水公司为F、河北工程大学为Y、银行为Ze

通过节水合同管理项目的节水测算，当F、Y与Z合作时，总收益V（F，Y，Z）=486.4万元；

假如联盟中无Y参与，V（F）=0，V（Z）=0，V（F，Z）=0。

假如Y不与F合作，而是自行改造节水设备，由于缺乏专业知识经验与技术设备，节水效果必然没有与节水服务公司合作好，按照总节水收益值20%取值得V（Y）=97.28万元；

假如Y与Z合作自行改造，按获得总收益的50%取值得V（Y，Z）=243.2万元；

假如F并未引入银行资金，则资金不能够满足实际需求，节水效益也会减少，按照总节水收益的80%取值得V（F，Y）= 389.12分别求得节水服务公司、用水客户与主要资金提供者节水收益分配初值如下：

2.3 确定影响因素权重及测度值

在得到初始分配方案后，需要对合作各方的投入比例、风险分担、努力水平、迫切程度等情况进行评估测度，确定利益分配影响因素权重及各评价对象i对各影响因素j的测度值aij。

（1）影响因素的权重

①建立影响因数权重判断矩阵

②一致性检验计算一致性检验指标CI

一致性检验结果：通过

③权重向量

计算得权重向量γ

（2）测度值的确定

①投入比重

根据各方投入的资金比列确定投入比重的测度值：

a11=0.31；a21=0.1；a31=0.59

②风险分担

多方合作项目中风险因素众多，可采用层次分析法根据各方所承担的技术风险、合同风险等程度不同确定风险分担测度值：

a12=0.47；a22=0.28；a32=0.25

③努力水平

多方合作项目中各合作方为了项目整体收益，根据项目合同约定的内容所做出的将项目运行向前推进的决策与行动的程度即努力水平，根据努力水平的不同确定努力水平测度值：

a13=0.65；a23=0.25；a33=0.10

④迫切程度

多方合作项目中各参与方根据自身需求对于该节水项目的迫切程度必然不同，据此确定迫切程度测度值：

a14=0.39；a24=0.49；a34=0.12

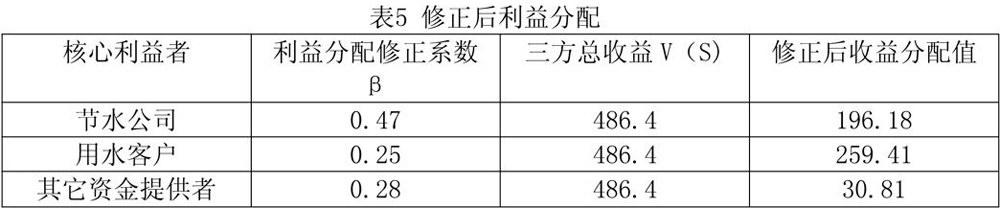
2.4 理想点原理综合修正

理想点原理通过测度各方参与者在多个影响因素方面的理想点距离，实现各因素重要程度的排序，以此来综合修正各参与者的利益分配比例。

（1）构造修正矩阵

设该项目中有3个利益相关者，即评价对象的集合为i={1，2，3}， 有4个修正因子，即评价指标的集合为j={1，2，3， 4}，评价对象i在修正因子j的测度值为aij，得到修正矩阵A

（2）确定理想点

根据标准化矩阵A可得各利益相关者在各修正因子的正理想解bj+和负理想解bj-，设b+、B-分别为正理想解数列和负理想解数列

bj+=max{bij}，bj-=min{bij}

B+=（b1+，b2+，…，bn+），B-=（b1-，b2-，…，bn-）

本文引入每个评价对象到理想点的欧式距离来对其进行修正，定义Di+为评

3 结语

本文在合同节水管理项目核心利益相关者利益分配中采用的算法，还可以推广到其它的领域中合同利益分配方面。只需先使用Shapley算法进行初值计算，然后根据具体情况改变影响因素权重与相关测度值即可较为方便的获得较为理想的利益分配结果。

参考文献：

[1]钟恒.合同节水管理模式在高校的应用研究[J].水利经济2017.

[2]李文华.基础于Shapley-理想点原理的PPP项目利益分配模型研究[D].西安建筑科技大学学位论文，2017.