基于监测资料的岸坡多层土体力学参数反演

刘学德，黄 铭，2

(1.合肥工业大学土木与水利工程学院，安徽合肥230009；2.三峡大学三峡库区地质灾害教育部重点实验室，湖北宜昌443000)

0 引 言

江河岸坡工程是为了保障江河沿岸人民生产生活的安全而修建的，我国沿江、沿海一带经济较为发达，岸坡工程的作用显得尤为重要。近年来，由于大型水利工程的修建，导致中下游河势变化明显，崩岸强度增加，给防洪工程安全、航道稳定、港口和取排水口运行等岸线开发利用带来十分不利的影响。

蠕动、失稳是岸坡工程经常遇到的问题。河水位变化导致岸坡蠕动变形加剧，对工程安全产生重大危害。因此，需对岸坡的蠕动变形进行监测，并采取不同措施防范其失稳破坏。采用数值模拟分析岸坡工程时，数值模型的仿真性和计算参数的准确性，对能否得到准确的计算结果起着重要的作用。在实际工程中，土体参数的确定方法主要包括现场试验法、室内试验法、参数反演法等。其中，现场试验法相对费时耗力，而室内试验法的一个显著缺陷是土体存在扰动，获得的土体参数与实际参数有一定的差别。采用反演方法可有效获得土体参数，省时省力，具有较高的准确性与可靠性。

岸坡工程的土体存在分层现象，随着深度的变化土体性质发生变化，土体参数也随之改变。本次研究中，采用同时反演法与分层迭代反演法分别反演各层土体参数，然后利用得到的土体参数，使用有限元软件，对岸坡工程进行位移场分析，对比不同水位作用下测点处的计算位移与实测位移，综合比较2种反演方法的合理性和准确性。

1 BP神经网络

BP神经网络应用广泛，适用性好。网络的学习过程由信息的正向传播和误差的反向传播组成[1]，基本结构见图1。图中，xj表示输入层第j个节点的输入；Ok表示输出层第k个节点的输出；wij表示隐含层第i个节点到输入层第j个节点的权值；vkd表示输出层第k个节点到隐含层第i个节点的权值；θi为隐含层第i个节点的阈值；αk为输出层第k个节点的阈值；φ、ψ分别表示隐含层及输出层的激励函数。

图1 BP神经网络结构

输入层各神经元负责接收外界信息，并传递给隐含层各神经元；隐含层负责信息变换，然后将变换后的信息传递到输出层，完成一次学习的正向传播。当输出结果与期望值不相同时，进入误差的反向传播阶段。误差通过输出层，按误差梯度下降的方式修正各层权值，向后逐层反向传播。通过信息正向传播和误差反向传播，使各层权值不断调整，循环往复，直至网络输出的误差满足精度要求，或达到预先设定的学习次数。

2 反演方法

2.1 同时反演

(1)反演变量。土体的弹性模量E是影响岸坡位移场的重要力学参数。根据岸坡典型剖面建立二维有限元模型。本文研究中，按照土体性质将岸坡土体划分为上下2层，考虑上下2层土体性质不同，取反演变量E=[E1、E2]T。其中，E1、E2分别表示上下层土体的弹性模量。

(2)训练样本。通过有限元软件计算不同水位作用下的上下层土体测点处位移xt(t对应不同水位情况)，形成训练样本。通过设计出的N组弹性模量，便能计算得到N组训练样本[2]。

(3)网络学习。以xt为输入样本，上下2层土体的弹性模量E为输出样本，将N组训练样本代入到BP神经网络中，并以规定学习次数或误差精度为收敛条件，然后将训练结果保存。

(4)弹性模量反演。将实测位移代入到训练好的神经网络中，即可反演得到土体的弹性模量值。

2.2 分层迭代反演

根据项目资料与试验数据，确定上下2层土体初始弹性模量[3]。从下层开始，先假定上层土体的弹性模量不变，利用不同水位作用下的下层土体测点位移，采用BP神经网络反演下层土体弹性模量，将反演结果代替该土层初始弹性模量，然后反演上层土体的弹性模量，将反演结果代替上层土体初始弹性模量。循环反演，直至前后2次反演的弹性模量的最大差值小于某一容许值为止[4]。

3 计算实例

3.1 岸坡弹塑性模型

某临江岸坡工程的边坡变形受江水位变化影响，临水侧以变化的江水位为水头荷载。根据土体性质，将岸坡土体分为上下2层，上层土体主要成分为粉质粘土，下层土体为粉细砂。岸坡典型剖面有限元模型见图2。

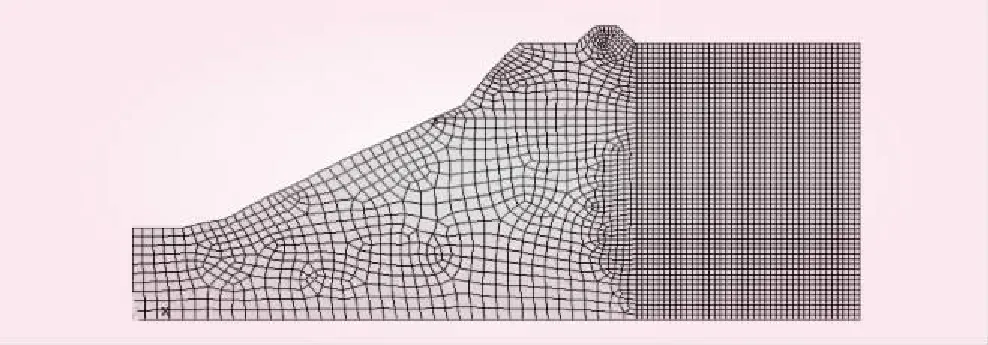
图2 岸坡典型剖面有限元模型

根据资料可知，岸坡工程上层土体天然重度γ为19.1 kN/m3、粘聚力c为15 kPa、内摩擦角Φ为15.3°；下层土体天然重度γ为18.8 kN/m3、粘聚力c为6 kPa、内摩擦角Φ为35.7°。参考相关试验可知，上层土体弹性模量的范围为8.0～18.0 MPa，下层土体为15.0～25.0 MPa。

2014年9月的一天，李淑荣接到勘探南方分公司打来的电话，旺1井需要尽快完成测井资料解释。作为在西藏部署的首口重点预探井，这口井的成败直接关系到整个西藏地区的勘探前景。可西藏冬季有封山期，距离甲方试油仅剩一个月的时间，留给测井解释的时间就更少了，只有48小时。

3.2 BP神经网络的学习样本

采用同时反演法时，利用ANSYS有限元软件分析岸坡位移场。本文将岸坡上下层土体中的测点分别记为A、B(测点位于土体具有代表性位置)，将A、B测点位移作为BP神经网络的输入层。取2016年2月24日～6月7日每隔1日的水位作为临江侧水头边界条件，每个测点可计算得到52个位移，神经网络的输入层共有104个节点，输出层为上下2层土体的弹性模量，输出层节点为2个。

根据均匀设计原理，将上下2层土体弹性模量分别设计成5个水平[5]，上层土体弹性模量分别为8.0、10.5、13.0、15.5 MPa和18.0 MPa，下层土体分别为15.0、17.5、20.0、22.5 MPa和25.0 MPa，最终设计成5×5个试验组。将这25组试验数据代入到有限元模型中模拟位移场，获得25组A、B测点位移，构成BP神经网络的训练样本。

采用分层迭代反演法时，1次反演1层土体的弹性模量。因此，只需计算该层土体测点位移，并以此形成神经网络的训练样本。如反演下层土体的弹性模量时，只需提取B测点的位移，此时神经网络输入层为52个节点，输出层为1个节点，将下层土体5个弹性模量代入有限元模型中进行位移场模拟，得到5组B测点的位移，形成BP神经网络的训练样本。反演上层土体弹性模量时，将上层土体弹性模量均匀设计成5个水平，通过位移场模拟可得5组A测点的位移，将其作为BP神经网络的训练样本。

3.3 BP网络的学习

获得训练样本后，应对样本数据进行预处理，目的是使数据同等重要，此外，数据处理还可防止神经元的过饱和情况。采用下式把数据归一化到(0.1～0.9)的范围之内，即

网络隐含层节点数采用下式计算，即

式中，m为隐含层节点数；n为输入层节点数；l为输出层节点数；β为1～10之间的整数。

采用分层迭代反演法与同时反演法时，BP神经网络的结构分别为52×10×1与104×12×2。把最大训练次数等于10 000次作为收敛条件，2种BP神经网络的误差与训练次数关系见图3。其中，分层迭代反演法的误差曲线为最后1次反演，即上层土体弹性模量确定情况下，反演下层土体弹性模量所得的误差曲线。从图3可知，相同训练次数时，分层迭代反演法比同时反演法的收敛速度更快、精度更高。

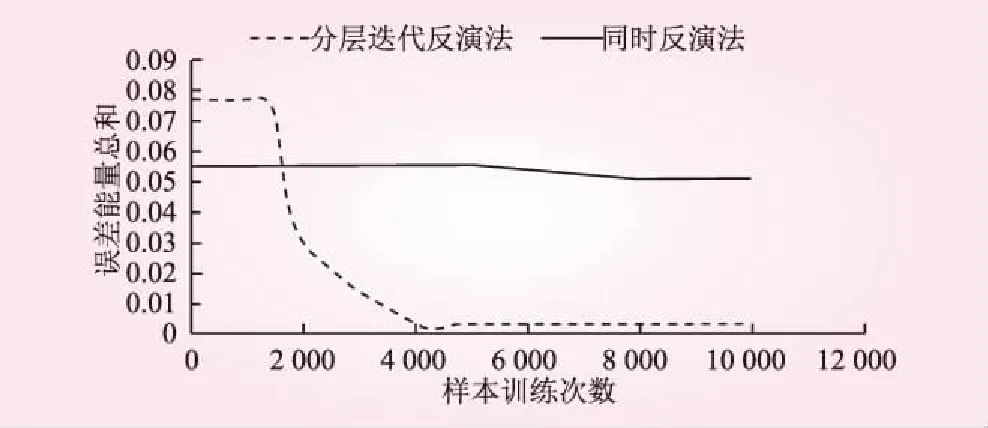
图3 BP神经网络误差

(3)

3.4 反演验证及分析

采用同时反演法时，利用25组A、B测点计算位移构成的样本训练BP神经网络，然后将A、B测点的实测位移代入训练好的BP神经网络中，反演得上下2层土体的弹性模量分别为12.98、20.024 MPa。为了验证反演结果的准确性，取2016年6月7日～7月2日的水位作为有限元模型的边界荷载。水位变化情况见图4。

图4 水位变化情况

将反演的弹性模量代入到ANSYS有限元模型中计算A、B测点的位移[6]，A、B测点的计算位移与实测位移见图5。从图5可知，计算位移随时间变化序列趋势与实测位移随时间变化序列趋势基本相符。采用下式计算A、B测点计算位移与实测位移误差均值，即

(4)

式中，μ为误差均值；Xt为实测位移；N为位移总数。经计算，A、B测点计算位移与实测位移误差均值分别为0.425 4、0.506 5 mm。

图5 实测位移与计算位移对比

采用分层迭代反演法时，分别利用A、B测点计算位移构成的样本训练BP神经网络，然后将A、B测点实测位移分别代入训练好的BP神经网络中，反演可得上下层土体的弹性模量分别为12.208、20.011 MPa。利用反演的弹性模量，通过ANSYS有限元软件，计算A、B测点位移。A、B测点计算位移与实测位移见图6。从图6可知，A、B测点计算位移序列趋势与实测位移序列趋势符合程度更高。A、B测点计算位移与实测位移误差均值分别为0.340 04、0.473 2 mm。

A测点实测位移波动较大，这是由于数据采集误差所致。A测点计算位移与水位对比可知，利用反演参数计算的A测点计算位移与水位变化一致性明显，呼应度较高，也符合实测位移的整体变化趋势，反演后计算结果理想。

比较2种反演方法，由各自所得弹性模量计算的A、B测点计算位移与实测位移的误差均值可知，分层迭代反演法误差均值比同时反演法小，说明分层迭代反演法精度较高。此外，分层迭代反演法比同时反演法的BP神经网络收敛速度更快。

4 结 语

岸坡工程位移变化受水位影响，本文利用有限元软件对其位移场进行分析，分别采用同时反演法

与分层迭代反演法反演岸坡土体弹性模量。为了验证结果的准确性，将2种反演结果分别代入有限元软件中计算测点位移，然后比较测点计算位移与实测位移。算例及分析表明，利用2种反演结果计算的测点计算位移与实测位移均相符；利用分层迭代反演法反演结果计算的测点计算位移与实测位移相符程度更高，拟合效果更好，并且分层迭代反演法反演时所用的神经网络收敛速度更快、误差更小。

图6 实测位移与计算位移对比