三维重建中线段匹配方法的研究
2018-08-17陈起凤雷光元董广峰
陈起凤 ,刘 军*,李 威 ,雷光元 ,董广峰
1.智能机器人湖北省重点实验室(武汉工程大学),湖北 武汉 430205;2.武汉工程大学计算机科学与工程学院,湖北 武汉 430205;3.国投新疆罗布泊钾盐有限责任公司,新疆 哈密 893000
随着信息技术的迅猛发展,三维重建在许多领域有越来越多的应用,如文化遗产保护、文物研究、视频监控、动画电影制作、医学图像处理以及虚拟现实等[1-2]。在计算机视觉中[3-4],基于图像的三维重建技术是根据场景的两张或两张以上的二维图像,由计算机自动计算并匹配场景的二维几何信息和深度信息,最后建立三维模型的过程。传统三维重建是基于点的特征提取与匹配[5-8],三维点云模型在缺少纹理的地方重建精度较差,三维线段模型能提供更充分的结构信息,反映场景的几何拓扑关系[9]。要生成一个基于线段的三维重建模型需要建立来自不同图片的二维线段的对应关系,线段匹配[10-11]指在两组线段中建立对应关系的过程。早期Schimid等[12]提出一种在三视图间自动进行线匹配的方法,在已知相机姿态信息的情况下,建立基于强度的点向线段匹配的对应关系。2005年Bay等[13]提出借助宽基线图像进行线段匹配的方法,通过计算任意相邻线段上像素点的颜色直方图(Hue,Saturation,Value,HSV)来完成,后来一种基于块的线段描述方法[14]被提出,该方法能快速得到亚像素级别直线的位置,但未考虑尺度变化的自适应性,会造成某些块过短从而线段无法被提取的现象。2009年,梯度均值-标准差描述子(mean-standard line deviation,MSLD)算法[15]被提出,该方法建立在梯度直方图基础上,在视角存在缺陷和光照有变化的情况下实验结果良好,但缺少几何属性做约束条件,当存在尺度变换时线段匹配准确率较低。Kim等[16]提出一种利用共面二维线段相交透视不变性的线段匹配方法,在线段交点处通过归一化交叉相关系数进行匹配,但未与建筑外观相结合,在进行多视图三维重建时模型表面会出现空洞现象。针对上述问题,本文将外观和几何约束相结合,利用直线提取(line segment detector,LSD)算法[17]检测直线段。首先寻找相邻图片,然后在相邻图片间进行二维线段匹配,最后进行三维模型重建。
1 线段检测技术
LSD算法是一种能在线性时间内得到亚像素级准确度的直线段分割检测算法,将梯度方向作为判定像素点之间图像关系依据进行线段检测。该算法可分为6个步骤:1)图像缩放;2)梯度计算;3)梯度排序;4)梯度阈值;5)区域增长;6)矩形估计。首先计算每个像素点附近的线场角度,生成一个线场区域即单位向量域,其中所有向量都与通过基准点的水平线相切。该区域被分割为连通的若干部分,它们在一定的容忍度内有相同的水平线角度,这些连通的部分被称为水平线支撑区域。每个水平线支撑区域都是一个直线分割的备选区域,同时需要一个矩形与它对应,水平线支撑区域的主轴表示矩形的主方向。矩形中线场区域角度与矩形主方向在一定容忍度下保持一致的像素点称为对准点。统计出矩形区域像素个数以及对准点个数,通过判定准则判断水平线支撑区域是否为直线段。算法示意图如图1所示。

图1 LSD算法示意图:(a)图片,(b)线场区域,(c)水平线支撑区域,(d)对准点Fig.1 Schematic diagram of LSD algorithm:(a)image,(b)lever-line field,(c)line support regions,(d)aligned points
2 寻找相邻图片
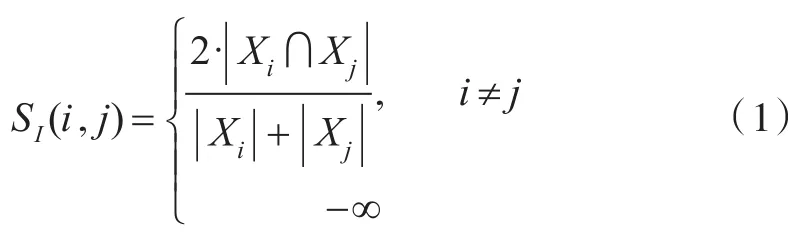
相似性评分越高表示两张图片重叠的部分越多,通过筛选相似性评分得到与图片Ii相邻的图片集合:
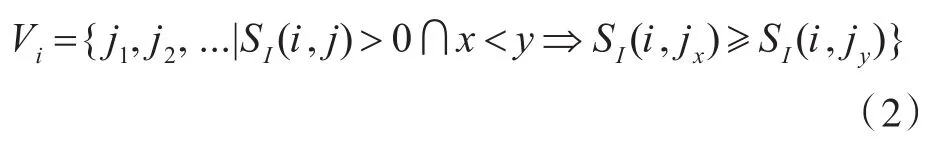
对于每个图片Ii,集合Vi仅包含所有相邻图片Ij的索引,并按照其视图相似性评分SI(i,j)降序排序。由于三维建模中数图片集的数据量较大并且任意两张图片都存在重叠部分的可能性较小,本文选取相邻图片进行二维线段筛选与匹配以达到高效建模的目的。本文使用相邻图片集合Vi中相似性评分最高的前M张图片即VM i,假设图片集I有N张图片,该算法时间复杂度为O(MN)。
3 二维线段匹配
假设二维线段集合Li与Lj分别存在于图片Ii与Ij中,在筛选完相邻图片后,选取相似度评分较高的M张图片,相邻图片Ii与Ij应满足条件二维线段匹配阶段只需进行集合Li与Lj的线段匹配。
根据对极几何知识,本文利用极线约束关系进行二维线段间的匹配。当且时,首先计算的端点与在另一张图片中的极线,得到两条极线与图片Ij中的二维段相交,获得与二维线段的端点与共线的两个交点χ1和χ2,如图2所示。
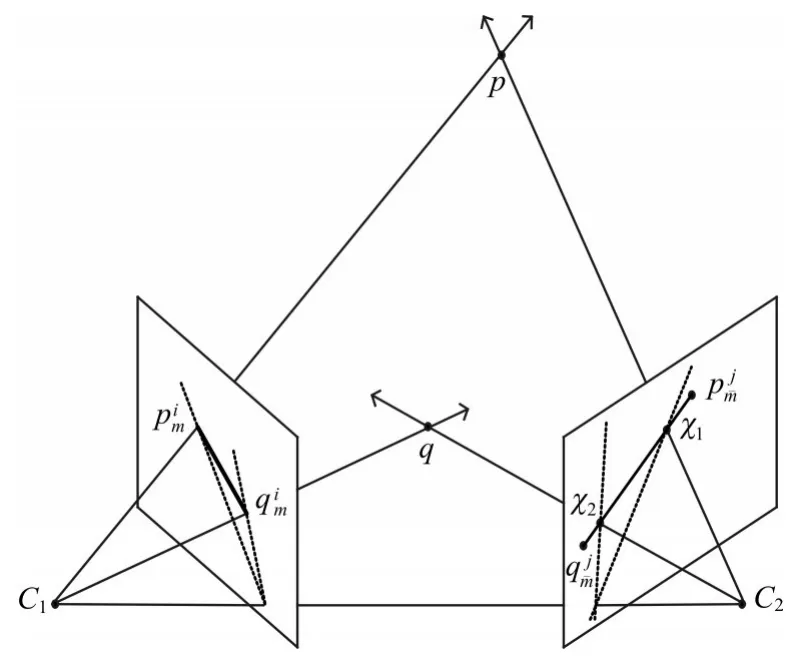
图2 二维线段匹配图Fig.2 Matched image of two-dimensional line segments
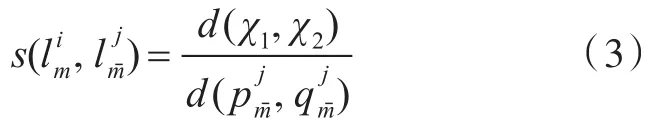
其中,d(χ1,χ2)与表示两个二维端点之间的欧几里得距离。由图2看出,四个端点共线。如果这两个二维线段是同一个三维模型的测量结果,理想情况下匹配得分的值为1。由于光照变化、镜头畸形、相机参数变化、拍摄角度改变等因素,对匹配得分有一定影响,本文只取大于一个定值的一部分集合。假设当匹配得分超过阈值τ时,二维线段与视为一组潜在的匹配线段。
通过阈值筛选,二维线段匹配程序拥有较高的查全率,但查准率很低。单纯提高阈值,在线段检测时会存在检测不精确的问题,本文选取K个与特定二维线段潜在相匹配的线段。二维线段匹配阶段提到了三个重要参数值:二维线段匹配阈值τ、相邻图片个数M、在相邻图中与特定二维线段相匹配的线段个数K。本文将这三个参数分为两组进行评估分析:首先对τ单独进行分析,然后将M与K组合进行分析。
4 结果与讨论
首先用小米无人机、iphone手机、索尼微单相机对武汉工程大学(Wuhan Institute of Technology,WIT)校园建筑进行了3组图片集采集。分别为36张的武汉工程大学图书馆图片集、41张的武汉工程大学教务处图片集、250张的武汉工程大学全景图片集,另外本文选取了PHOTOSCAN软件中50张建模实例图片集。然后,对这4组图片集进行重建实验。
4.1 二维线段匹配阈值τ对重建结果的影响
二维线段匹配阈值τ默认值设置为0.25,即两种可能匹配的二维线段的相互重叠率至少要达到25%。为了获得最佳的阈值,选取5个值0.1、0.25、0.5、0.75、0.9进行对比试验。其中0.1表示二维线段极少重叠,0.9表示二维线段几乎完全重叠。实验结果如表1所示。不同阈值τ下图书馆重建模型如图3所示。
数据表1与图3表明三维模型中的三维线段数量与极线重叠阈值成反比,当阈值增加时,三维线段数量递减;运行时间也与阈值成反比,阈值越小,所花费的时间越长。当阈值低于0.5时,重建模型相对稳定,当阈值超过0.5,重建线段数会减少,三维模型会逐渐模糊,尤其在阈值等于0.9时,重建模型线段数锐减,模型完全不符合预期效果。根据实验结果得出结论:极线重叠阈值应该选择一个较小的值,一般低于0.5更合适,这样可以降低误删正确线匹配的可能性。
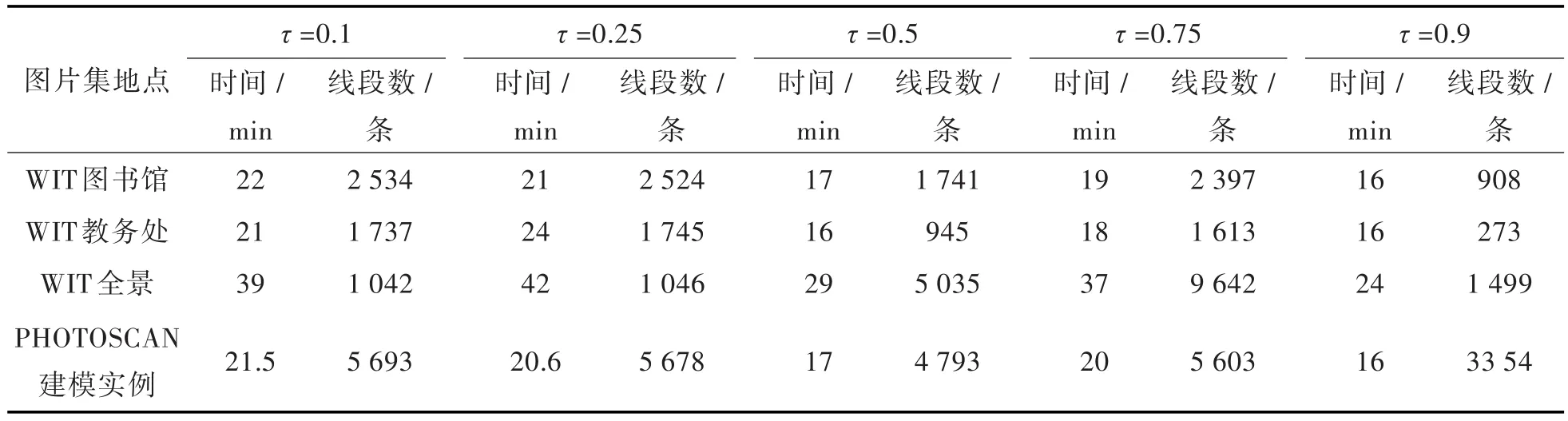
表1 不同二维线段匹配阈值τ下的重建时间与线段数Tab.1 Time and line numbers of 3D reconstruction under differentτ

图3 不同阈值 τ对WIT图书馆三维重建模型的影响:(a)0.1,(b)0.25,(c)0.5,(d)0.75,(e)0.9Fig.3 Effects of different τon 3D reconstruction of library of WIT:(a)0.1,(b)0.25,(c)0.5,(d)0.75,(e)0.9
4.2 M和K对重建结果的影响
相邻图片个数M、在相邻图像中与特定二维线段相匹配的线段数K默认值是10,表示选取每张图片最相邻的10张图片,在可视相邻图片中与某个二维线段相匹配的个数限制为10条。M与K的乘积表示潜在匹配二维线段的总数,在不考虑运行时间的情况下,M与K乘积越大,重建的结果越精确。
为了分析M与K单个参数对重建结果的影响,本文选取WIT图书馆图片集,对M与K分别取M∈{5,10,20}与K∈{1,5,10,20}组合实验,得到12组重建结果,实验数据总表如表2所示,不同M、K对重建结果的运行时间和线段数影响如图4所示。
当拥有充足的运行时间预算时,选用越大的M、K值,重建线段数越多,得到的重建结果会越精密。M选取值为5、20时,重建时间一直随K值增大而增大。M选取值为10,当K值小于5时,重建时间随K值增大而增大;当K值选取5到10时,重建时间随K值增大而减小,K值为10时,重建时间最短;K值由10增到20时,重建时间与K值成正比。

表2 不同M、K下的图书馆图片集重建时间与线段数Tab.2 Time and line numbers of 3D reconstruction of library of WIT at different M,K
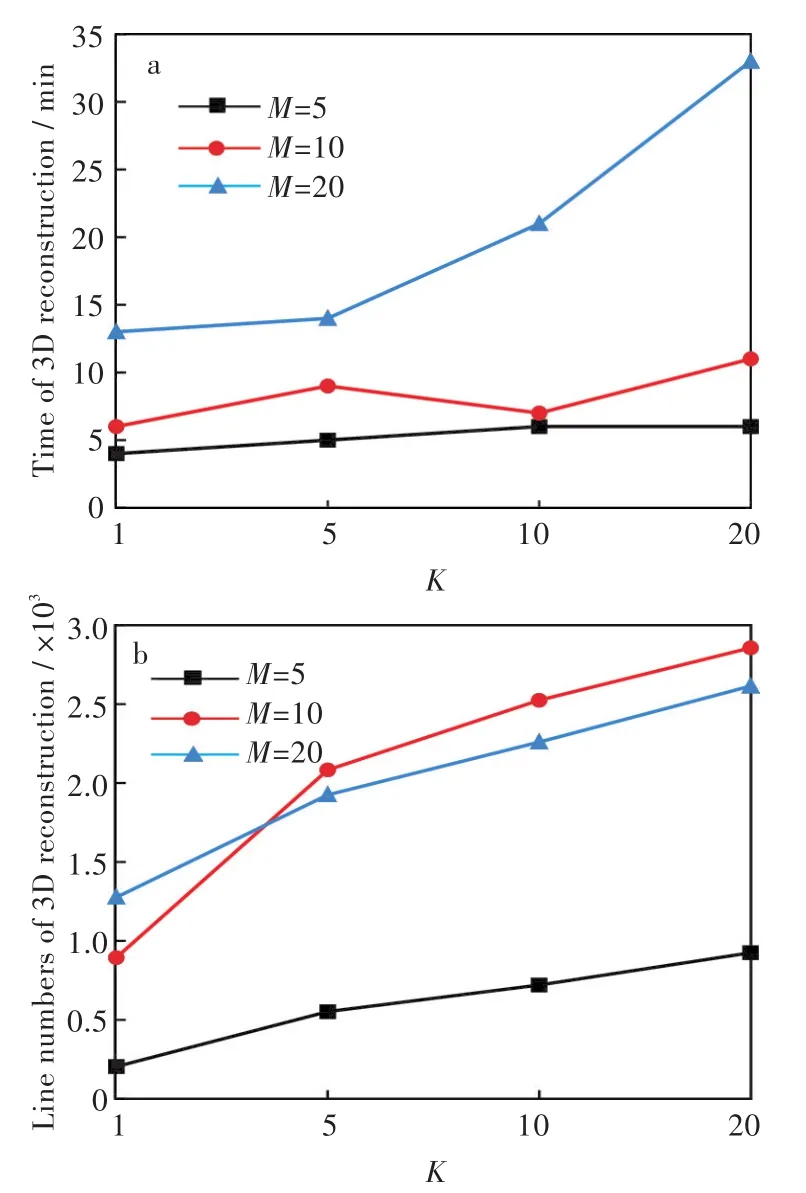
图4 不同M、K对重建结果的影响:(a)时间,(b)线段数Fig.4 Effects of different M,K of 3D reconstruction on(a)time,(b)line numbers
综上所述,选用M=10、K=10组合时,能够接近最佳重建效果并保证算法拥有较低的时间复杂度。
5 结 语
利用LSD线段提取算法检测出图片集中二维线段,在二维线段匹配阶段,对二维线段匹配阈值τ、相邻图片个数M、在相邻图像中与特定二维线段相匹配的线段个数K三个重要参数进行评估,实验结果表明当阈值τ低于0.5,M=10,K=10时三维建模效果最好并且运行时间可接受度较高,为后续对三维重建算法优化提供依据。
