多尺度残差深度神经网络的卫星图像超分辨率算法

汪家明，卢 涛

武汉工程大学计算机科学与工程学院，湖北 武汉 430205

遥感卫星是一种重要的对地观测手段，能够对地面进行大面积的同步观测以获得地面目标的信息。遥感卫星图像在灾害监测预警、资源勘探、和环境检测等领域有着广泛的应用前景。然而，由于硬件设备与成本的限制，遥感图像的分辨率固定。此外，大气湍流、成像过程噪声、设备与景物之间的运动模糊、光学传感器的欠采样，降低了卫星图像的分辨率和质量。为了提高遥感影像的空间分辨率，克服噪声和成像模糊的影响，对遥感图像的超分辨率重建显得尤为迫切。

现有的图像超分辨率重建算法（super-resolu⁃tion，SR）主要分为2类：基于重建的算法和基于学习的算法。基于重建的算法通过多个低分辨率图像来融合亚像素精度的多帧信息［1］，重建出更高分辨率的图像。但基于重建的方法仅能利用低分辨率图像之间的互补信息，不能增加新的高频信息，因此这类重建方法的放大倍数有限。然而后续的识别任务更加关注高频信息中包含的特征［2］。近年来，受到机器学习理论发展的影响，基于学习的方法受到高度的重视日益成为超分辨率算法研究的主流方向。基于学习的算法通过训练样本提供的先验信息，学习低分辨率图像块与高分辨率图像块之间的映射模型。从训练样本的使用角度来看，基于学习的算法可以分为3类：基于表达的超分辨率算法，基于回归的超分辨率算法和基于深度学习的超分辨率算法。

基于表达的算法根据高分辨图像在不同分辨率空间表达系数不变这一性质，使用低分辨字典表示输入图像块，并找寻低分辨率字典对应的高分辨率字典进行重建［3-4］。基于回归的算法通过回归模型对超分重建进行求解［5-6］。考虑到卷积神经网络（convolutional neural network，CNN）的优秀学习能力，通过卷积神经网络［7-8］来学习低分辨率和高分辨图像之间的复杂非线性映射关系，通过多个隐藏层来扩展传统网络的深度。Shi等［9］构建了亚像素空间的卷积神经网络，直接而高效地学习了从低分辨率图像到高分辨率图像的映射函数。Kim等［10］通过深度残差网络证明了深度残差网络层数对于超分辨率性能有提升。生成对抗网络［11］由生成网络和判别网络组成，通过生成网络生成细节，取得了良好的视觉效果，但是客观指标较低。Luo等［12］在 Kim［10］的基础上根据自相似性填充图像取代零填充，避免增加无用的信息，在卫星图像超分辨率任务中表现出了优异的重建效果。

卫星图像超分辨率是特定领域的超分辨率重建问题，准确的边缘和纹理等高频信息对于卫星图像检测和识别任务是至关重要的［13］。待识别目标的全局高频信息在检测任务中占据主导地位，而局部的高频信息在识别任务中不可或缺。但是遥感卫星图像成像范围广，目标的尺度差异较大，直接使用同构同质的网络预测重建不同尺度的目标，导致重建精度不满足要求或者效率低下。而现有的基于多尺度的超分辨率算法中，多尺度信息融合是在像素域或特征域进行，重建结果注重的是图像的内容和局部高频信息，却忽略了全局的高频信息。因此需要一个网络结构，可以灵活处理不同尺度的目标和不同精度的超分辨率任务，预测出不同尺度目标的边缘和纹理等高频信息，并在更加快速和有效的残差空间融合多尺度信息。综合考虑上述问题，本文提出了一个多尺度残差深度神经网络的卫星图像超分辨率算法。

1 基于多尺度残差深度神经网络的卫星图像超分辨率

结合多尺度图像分析和深度残差网络，将同一卫星图像以多尺度的形式放入不同的深度残差神经网络中，建立不同尺度特征的自适应深度神经网络，学习从底层到高层的特征，预测不同尺度空间的高频残差信息。然后通过残差融合网络将预测所得的不同尺度空间的残差图像在残差空间进行加权，进行残差信息之间的互补和融合，使得不同目标能够在最合适的空间进行表达。本文中的多尺度残差网络以两个不同尺度空间子网络为例，分别为尺度空间1和尺度空间2，网络结构图如图1所示。

1.1 残差学习

Kim［10］证明了随着网络层数的增加，大量的超参数促进了网络的非线性表达能力。然而，网络层数的单一级联带了一个不可避免的问题：梯度消失/梯度爆炸导致在反向传播中网络的参数无法优化［14］。由于输入的低分辨率图像和原始高分辨率图像非常相似，本文定义残差图像为ri=yi-xi。残差图像的像素值大多数为零或者较小值。低分辨率图像的插值结果xi属于原始图像yi的低频分量，因此残差图像ri为yi的高频分量。相比直接预测像素域的图像，使用残差学习不仅会大量减少网络携带的信息，可加快网络收敛速度，还可以避免深度网络的不收敛问题［10］。

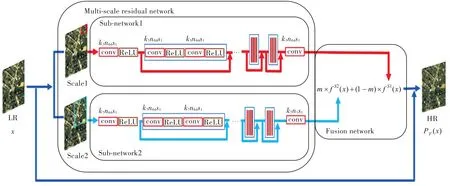
图1 多尺度残差网络的网络结构。网络包括多尺度残差学习网络和残差融合网络两部分（k表示卷积核大小，n表示卷积核个数，s表示步长）Fig.1 Network architecture of multi-scale residual deep neural network.The network includes two subnetworks：multi-scale residual network and residual fusion network.（k is the convolution kernel size，n is the number of convolution kernel and s is stride size）

1.2 多尺度特征提取

在尺度空间1残差学习网络中，本文使用大小为41×41像素的重叠图像块进行训练。本文定义卷积核大小为3×3。网络输出的残差为：

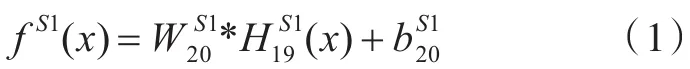
其中fS1(x)为尺度空间1残差学习网络预测所得的残差。为尺度空间1残差学习网络第19层输出的特征图。卷积的权值大小为64×3×3×1，偏置项大小为1×1。

在尺度空间2残差学习网络中使用100×100的非重叠图像块。由于输入图像块大小的增加，所以需要更大的感受野。本文定义卷积核大小为7×7，尺度空间1和尺度空间2残差空间增强网络相似。网络输出的残差为：

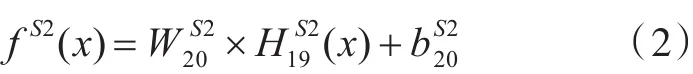
其中fS2(x)为尺度空间2残差学习网络预测所得的残差。为残差学习网络第19层输出的特征图。卷积的权值大小为64×7×7×1，偏置项大小为1×1。

1.3 残差融合网络

相同尺度的目标在不同的尺度空间具有不同的表达形式［15］，本文通过不同尺度空间找寻不同尺度的目标的最适合的表达形式，并通过多尺度的表达形式进行信息互补，保证了目标表达的准确性。本文试图通过融合模型组合尺度空间1的残差信息和尺度空间2的残差信息。融合后的残差为：

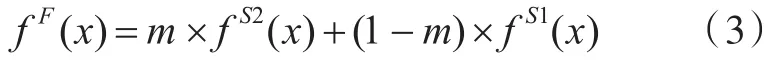
其中m表示尺度空间2预测残差的权重，在本文中m=0.9。最终的重建图像为：

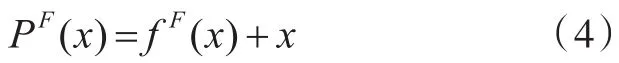
1 .4 损失函数

使用均方误差（mean squared error，MSE）作为网络的损失函数，整体的损失函数为：

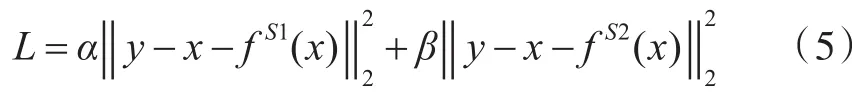
其中α，β控制不同尺度残差学习网络之间的平衡，在本文中α=β=1。网络优化过程中使用梯度下降法来进行反向传播。每次卷积操作都会缩小特征图的大小，通过填充零来保留更多的边缘像素，以更准确地推断中心像素，同时也确保了所有的特征图大小相同。网络损失如图2所示，由于2个子网络训练使用的图像块大小差异，所以对应的网络训练时的损失在量级有差异，但收敛趋势相同，证明了使用不同尺度的残差网络恢复残差的合理性。

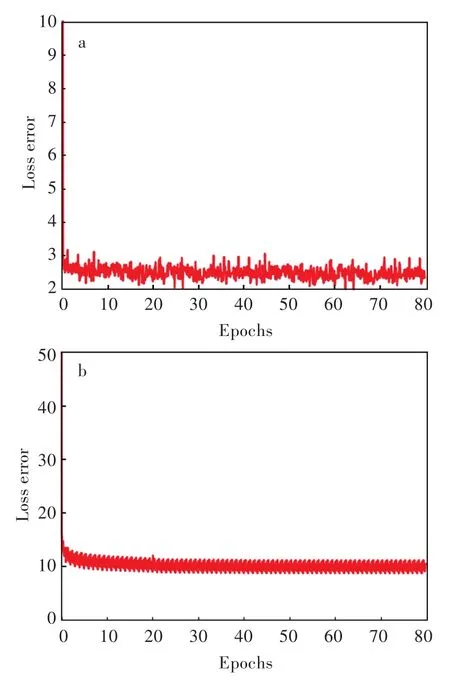
图2 不同尺度残差网络的训练损失图：（a）尺度1，（b）尺度2Fig.2 Training loss of multi-scale residual networks：（a）scale 1，（b）scale 2

2 结果与讨论

2.1 实验数据与参数

本文在Space Net卫星图像数据集中进行实验，并通过峰值信噪比（peak signal to noise ratio，PSNR）本文中定义为RPSNR、结构相似性（structural similarity，SSIM）和互信息（mutual information，MI）作为重建图片质量的客观评估标准。PSNR和SSIM从图像的角度刻画了重建图像与原始图像之间的相似性，而互信息可从信息的角度表示两幅图像之间的信息的依赖程度，互信息评分越高，图像之间的依赖越高，图像之间的相似性也越高。图像x与y之间的互信息定义为：

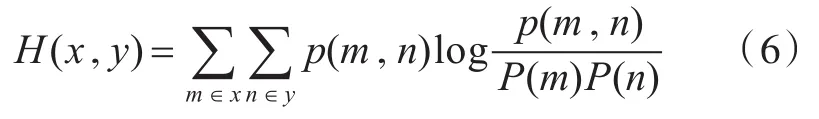
式（6）中，m和n表示灰度值，P(m)表示灰度值为m的像素数量占整幅图像的比例。

Space Net卫星图像数据集中包括里约热内卢、巴黎、拉斯维加斯、上海和喀土穆5个可用的区域，每个地图图像都由完整的高分辨率卫星图像分割为438×406像素的RGB图像，图像的兴趣内容主要为建筑和道路等。从里约热内卢地图中随机选取240张建筑群图像，其中的160张作为训练集，40张作为验证集，余下40张作为测试样本。

本文算法网络为并行网络结构，每个子网络都需要训练80个时期。由于网络层数较深，因此本文算法使用学习率衰减，学习率初始化为0.1，每隔20个时期学习率便会下降至原来的1/10，而网络的动量为0.9。为了避免过拟合，本文使用ℓ2正则化，其权值衰减为0.0001。在尺度空间1残差学习网络中，本文设置步长为1，填充为1，而尺度空间2残差学习网络中，设置步长为1，填充为3。本文使用msra来初始化权重，即满足均值为0方差为的高斯分布（n输入训练样本的个数），使用constant来初始化偏置项，即初始值为0。实验先将RGB图像转换到YCbCr颜色空间，在Y通道中进行重建，重建完成后再将Y通道的图像还原到RGB颜色空间。

2.2 实验结果与分析

对结果进行定量和定性的分析，并使用PSNR、SSIM和MI用于评估重建的结果进行定量分析。此外为了验证本文算法网络结构的有效性，比较了CNN中前沿的算法：加速的基于卷积网络的图像超分辨率算法（auelerating the super_reso⁃lution convolutional neural network，FSRCNN）［16］，经典深度学习算法基于深度卷积网络的图像超分辨率算法（image super-resolution using deep convo⁃lutional networks，SRCNN）［7］的加速优化版本，拉普拉斯金字塔超分辨率网络（laplacian pyramid su⁃per-resolution networks，LapSRN）［17］，视频卫星图像超分辨率算法（video satellite imayery super resolu⁃tion，VISR）［12］。本文中使用的对比算法 FSRCNN的源代码由论文作者Chao Dong提供，LapSRN的源代码由论文作者Wei-Sheng Lai提供，VISR的源代码由论文作者Yimin Luo提供。所有测试图像的PSNR和SSIM如图3所示（由于FSRCNN的客观评分过低，并未在图3中展示），本文算法重建图像的PSNR和SSIM都是最优的，如表1所示，本文算法无论是PSNR、SSIM还是MI都获得了最高的客观评分。与性能排名第二的算法VISR相比，分别提升了0.25 dB，0.01和0.03，表明了多尺度的残差网络通过不同尺度空间更有效地学习图像内容和结构，以及通过更深网络恢复图像的信息的有效性。

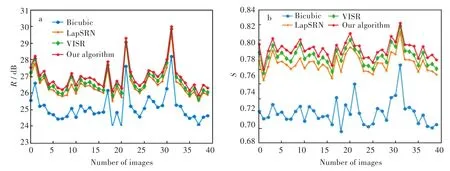
图3 Space Net卫星图像超分辨率结果的客观对比：（a）PSNR，（b）SSIMFig.3 Objective results of super-resolution algorithms over Space Net satellite images：（a）PSNR，（b）SSIM

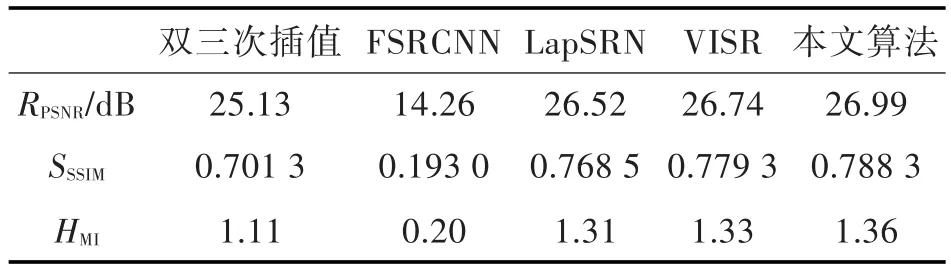
表1 Space Net数据集上PSNR，SSIM和MI的平均结果Tab.1 Average results of PSNR，SSIM and MI on SpaceNet dataset

2.2.1 本文算法与FSRCNN对比 FSRCNN使用亚像素空间来取代SRCNN在像素域的计算，但是FSRCNN中输入的低分辨率图像块大小为11×11像素，对应的高分辨率图像块大小为19×19像素，因此并不适用于尺度差异较大的卫星图像，如图4所示，FSRCNN有较好的重建效果，但是由于尺度问题，导致重建图4（b）中图像块拼接处不平滑，客观评分较低。

图4 SpaceNet卫星图像超分辨率结果的主观对比：（a）双三次插值，（b）FSRCNN，（c）LapSRN，（d）VISR，（e）本文算法，（f）高分辨图像Fig.4 Subjective results of different super-resolution algorithms over SpaceNet satellite images：（a）bicubic，（b）FSRCNN，（c）LapSRN，（d）VISR，（e）our algorithm，（f）high resolution image

2.2.2 本文算法与LapSRN对比 LapSRN为多尺度的深度学习算法，但是LapSRN的多尺度信息融合主要是在训练网络中的特征域进行。而本文算法则是通过构建并行网络，在残差域中进行融合。残差空间与图像的高频信息之间联系更为紧密，且残差域中数值较小，携带的信息量较小，能够有更高的计算效率。

2.2.3 本文算法与VISR对比 VISR通过对低分辨图像进行自相似填充，来避免网络中的零填充带来无用的信息，但是也因此将网络改变为像素域。像素域中的重建会更多的关注于图像中的低频信息内容，而卫星图像超分辨率任务中更希望恢复的是高频信息，且在残差域网络中更为高效。

由图4图像重建客观结果来看，该算法的重建图像比其他算法的结果包含更多的细节信息。使用本文的算法重建的高分辨率图像拥有更多的高频信息。例如，对于小目标建筑，本文的算法使房屋的轮廓更清晰；对于大目标建筑，本文的算法在屋顶的纹理方面有更好的表现；对于建筑间的道路，本文的方法更清晰的重建出了道路中的细纹。总之，由本文的结果证明，使用多尺度的残差网络有助于卫星图像的超分辨复原。

3 结 语

考虑到卫星图像的特殊性，使用多尺度学习来提高卷积神经网络对遥感卫星图像不同尺度先验信息的适应能力，通过融合多尺度残差得到更准确的边缘和纹理等高频信息。在Space Net数据集上的实验结果表明：提出的多尺度残差深度神经网络能有效地增强重建图像中的高频信息，相比前沿的卫星图像而言具有更好的主客观重建质量。