带有多重空间干涉约束的工程调度优化
2018-08-17陶莎盛昭瀚
陶莎,盛昭瀚
(南京大学 工程管理学院,南京 210093)
工程调度是工程现场协调控制的重要任务,其本质上是对一组相互关联的活动进行资源分配[1-3]。空间资源是指工程活动执行过程中对施工现场三维空间的占用[4-5]。为加快工程施工进度,缩短交付期,工程管理者常常安排多个活动并行执行,使得单位时间内空间需求总量增加,引起空间干涉,如空间冲突、拥挤,导致作业效率降低或中断、参建主体间发生冲突,甚至会引发安全事故[6-7]。因此,工程空间资源调度目标是确保在施工现场并行开展多种作业活动时,最大程度地规避空间干涉,确保作业空间充足、有效[8]。
许多学者基于计算机仿真和可视化技术(如4D CAD、BIM 等),设计活动空间干涉识别与应对的流程和方法[9-12]。Zhang等[10]在BIM 中融入遥感技术,利用GPS定位系统跟踪施工人员位置并实时判断其作业空间,基于BIM 平台将作业空间信息可视化,进而识别潜在的空间干涉并及时应对。Choi等[11]设计了一种作业空间规划的流程框架,包括生成4D BIM、识别作业空间、表征空间占用、识别空间干涉以及解决空间干涉问题等5个阶段,避免施工中的空间干涉及其不良影响。这类研究主要是在已知调度计划方案的前提之下,实时地、局部地识别空间干涉并调整调度方案,但缺乏考虑空间干涉的总体调度方案设计的理论研究。
另外,经典的资源受限项目调度问题(RCPSP)模型时常被应用于工程领域。RCPSP 解决的问题是在满足项目活动的工序和资源量限制的前提下,制定调度方案以达到工期最短、成本最低、资源利用率最大等目标[13-14]。RCPSP问题中,受限的资源并没有具体的指代,而是将资源类型大致分为可再生资源(如人力资源)和非再生资源(如材料资源等),并将两类受限资源的一般性特征体现在不同的约束式中,包括非再生资源总量限制约束以及可再生资源在每个时段上的用量限制约束。近年来,关于RCPSP的研究主要集中在优化算法设计上。由于RCPSP是典型的NP-hard问题,研究表明,许多启发式算法,如模拟退火、遗传算法、粒子群算法等,在解决RCPSP及其延伸问题(如多模式资源受限的项目调度问题)时,在算法性能、拓展性、操作便利性等方面均更具优势[15-16]。空间资源作为一类有限的可再生资源,是RCPSP 问题中的受限资源的具体化,因此,RCPSP模型及相关算法设计对其也适用。但目前鲜有学者将项目调度理论模型与空间干涉问题相结合。
综上所述,可以看出,关于考虑空间干涉特征的总体工程调度方案设计,建立考虑空间干涉约束的工程调度优化理论模型等方面的研究尚未深入开展。为此,本文创新性地研究考虑空间干涉的工程调度优化问题,对工程的空间资源和空间干涉进行系统地分类,建立带有多重空间干涉约束的工程调度理论模型。为了有效求解该问题,创新性地设计了考虑多重空间干涉的调度生成机制,并提出一种禁忌模拟退火(Tabu Simulated Annealing,TSA)启发式算法。最后,围绕一个现实的工程案例和随机生成的算例群进行计算实验,验证模型和方法的有效性。
1 工程活动的空间需求与空间干涉
空间是工程活动实施的必要条件之一。工程活动涉及的材料、人、设备等资源以及工程构件都需要占据一定的空间[11]。按占用物内容和用途划分,工程活动空间需求可分为6类,分别为工程构件空间、人力空间、设备空间、危害空间、保护空间和临时空间[6]。
针对这6类空间,按空间占用物特性,可将其划分为:①实空间。空间的占用物是实际的、具体的,如设备、人员、工程的物理构件等。②虚空间。空间的占用物是虚拟的、抽象的,如危害空间、保护空间中的“危害”“保护”等。
进一步,按实体占用物对空间的独占性,实空间又可分为:①刚性空间。占用物所占用的空间不可被压缩,占用物对需求空间独占。例如,工程物理构件所占用的空间,大型设备所占用的空间。②弹性空间。占用物所占用的空间可以被一定程度的压缩,空间可以在一定程度上被其他活动占用。例如,人员或小型灵活型设备所需空间。
综上所述,空间分类关系图如图1所示。
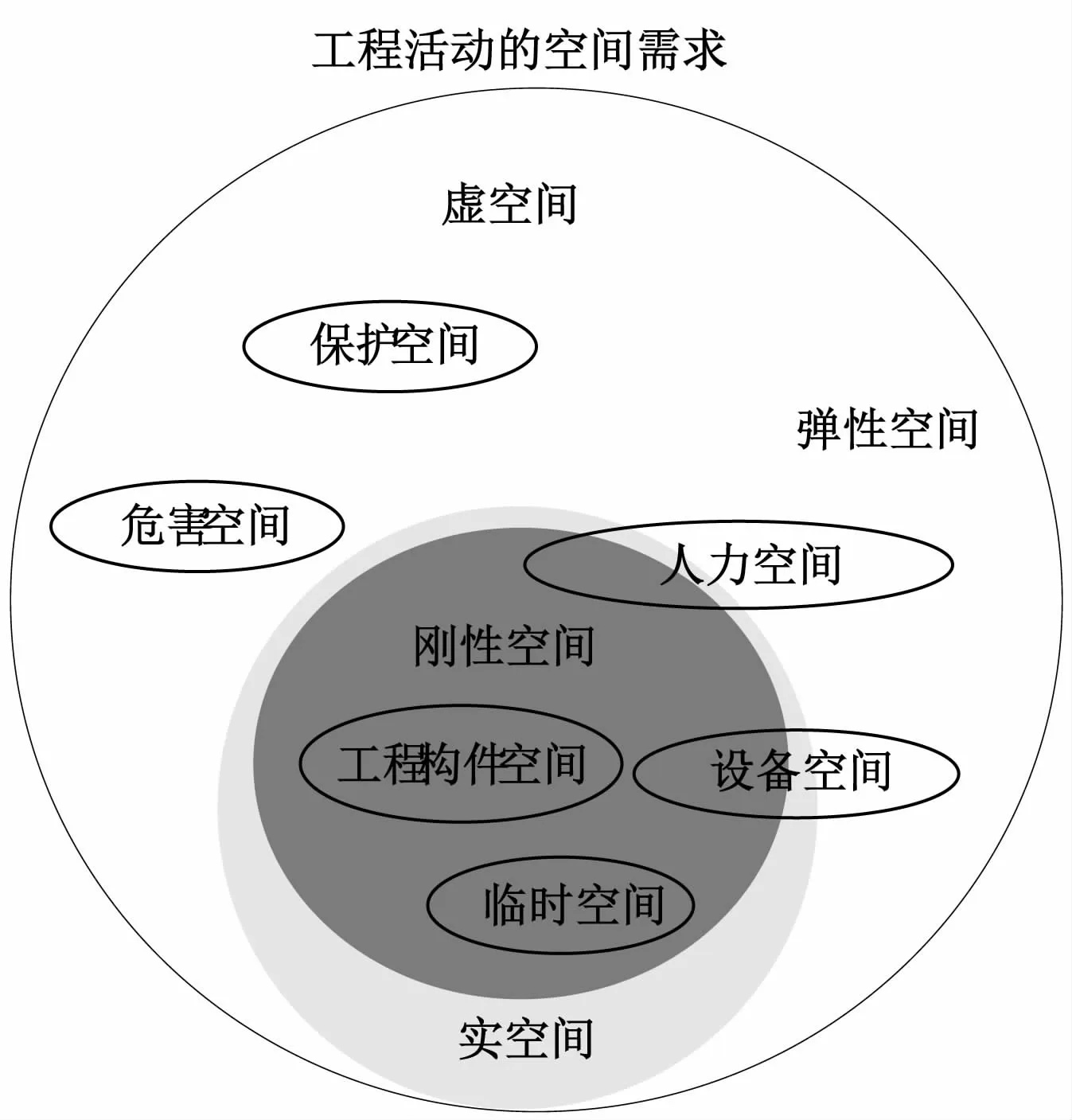
图1 空间资源分类示意图
空间干涉是指工程实施过程中,某作业活动所需的空间被其他活动占用,致使自身的作业空间不足,并进而引发各类不良后果。引发空间干涉的两个必要条件是:①活动并行,即执行时间存在重叠。②两个以上的活动占用同一空间,即空间需求存在重叠。不同的空间相互干涉会产生如下4种不同类型的后果:
(1)安全威胁。危害空间与人力空间的干涉。当一个活动的危害空间和另一活动的人力空间产生干涉时,会对员工生命安全造成威胁。例如,物体高空掉落。
(2)物理冲突。刚性空间与实空间的干涉。若空间被某些实体占用且被要求独占,则该空间排斥任何其他实体的占用。例如,某些物理结构。
(3)破坏冲突。保护空间与实空间、危害空间的干涉。保护空间可能被实空间中的实体或者危害空间产生的危险破坏。例如,混凝土养护。
(4)拥堵。弹性空间之间的干涉。弹性空间具有共享性,但拥挤的环境会引起人员或设备资源的安全性以及工作质量的下降,从而降低项目的整体质量[7,17]。
本文将安全威胁、物理冲突、破坏冲突统称为空间冲突。空间冲突一般表现为物理上的不可行或可能造成较严重的后果(破坏性的、危险的),在工程中应尽可能避免发生。轻度的弹性空间干涉可以提高空间利用率,提高活动的并行性从而加快项目进程,但过度拥堵会影响员工和设备的工作质量。因此,拥堵需要控制在一定范围内。
2 问题描述与一般数学模型
本研究是在经典的RCPSP 模型基础上,创新性地融入了各类空间干涉约束,使求解的最优调度方案不仅满足工序约束,还能避免和控制活动间的空间干涉,有效应对工程现场空间资源有限,活动空间易冲突或拥堵的实际场景。核心问题旨在已知活动工序、工期以及各类空间需求的条件下,安排各活动的开始时间,使其不仅满足活动工序约束,还能避免安全威胁、物理冲突和破坏冲突等3类空间冲突发生,并将拥堵控制在一定范围内,最终实现项目总完工时间最小化的目标。本研究的创新点和难点在于如何数学化表示各类空间干涉。
模型的建立基于4个前提假设:
(1)活动的各类空间需求已知且固定,空间需求不随时间而改变。
(2)活动所需的其他资源供应充足。
(3)安全威胁、物理冲突和破坏冲突是杜绝发生的,拥堵在一定程度上是被允许的。
(4)活动质量与拥堵程度呈线性负相关,即活动质量随着拥堵程度增加而线性降低。值得注意的是,本文建立的模型及算法并不局限于线性的质量影响函数,也可以采用其他函数形式,如二次、指数和S型曲线等。
采用AON(Activity-On-Node)的项目网络,记项目G={N,A}。AON 网络中节点集合N={1,2,…,}表示个项目活动,不失一般性,虚拟项目的开始和结束节点不妨记为O和Θ。0/1矩阵{aij},i,j∈N表示活动之间的工序关系,若i是j的紧前活动,则aij=1,否则为0。设项目整个计划的时间范围为[0,T],并离散化为时间片集合T= {1,2,…,N T},由N T个单位时间间隔构成。建立工程现场空间的三维坐标系,活动的各类空间均定义在该坐标系下。所有已知参数和变量符号含义:
d i—— 活动i的工期
—— 执行活动i需要的实空间
—— 执行活动i需要的刚性空间
—— 执行活动i需要的弹性空间
—— 执行活动i产生的危害空间
—— 执行活动i需要的人力空间
—— 执行活动i需要的保护空间
——活动i的弹性空间对被活动j的弹性空间占用的敏感性
Qi—— 可接受的活动i质量下限,Qi∈[0,1]
—— 活动i的质量对空间拥堵的敏感性
x i≥0—— 开始作业活动i的时间
Γt⊂N——t时间片上正在作业的活动集合
Λi⊂T—— 活动i正在作业的时间集合
∈[0,1]—— 活动i完成的拥堵因子
qi∈[0,1]—— 活动i完成的质量因子
fMS——项目总完工时间
基于上述符号定义,建立如下考虑空间干涉的工程调度优化的一般数学模型:

目标式(1)表示最小化项目完工时间fMS,即虚拟结束节点的开始时间。约束式(2)表示项目活动工序约束,活动的开始时间应不早于其紧前活动的结束时间。式(3)避免安全威胁、物理冲突和破坏冲突的任何一种空间冲突的发生,表示在任意时间片t上并行作业的活动关于3种空间冲突的空间需求都不重叠(重叠空间体积之和为0)。其中的三重积分计算空间的体积,空间重叠用交集运算符∩表示。例如,dxdydz计算活动i的危害空间和活动j的人力空间重叠的空间体积。式(4)计算执行活动i的拥堵因子,表示在活动工期内,活动i的总体弹性空间平均被其他活动占用总空间的百分比。其中,
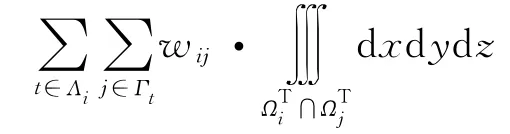

3 禁忌模拟退火算法
模拟退火算法(Simulated Annealing,SA)在求解许多NP-hard问题,尤其是项目调度问题方面具有操作简单和快速收敛的特点。为克服算法搜索陷入局部极值,提高收敛速度,本文在基本的模拟退火优化算法中引入禁忌表,设计TSA 算法。尤其在算法的调度生成机制(SGS)设计上,创新性地融入多重空间干涉约束,即避免安全威胁、物理冲突、破坏冲突以及控制拥堵程度。

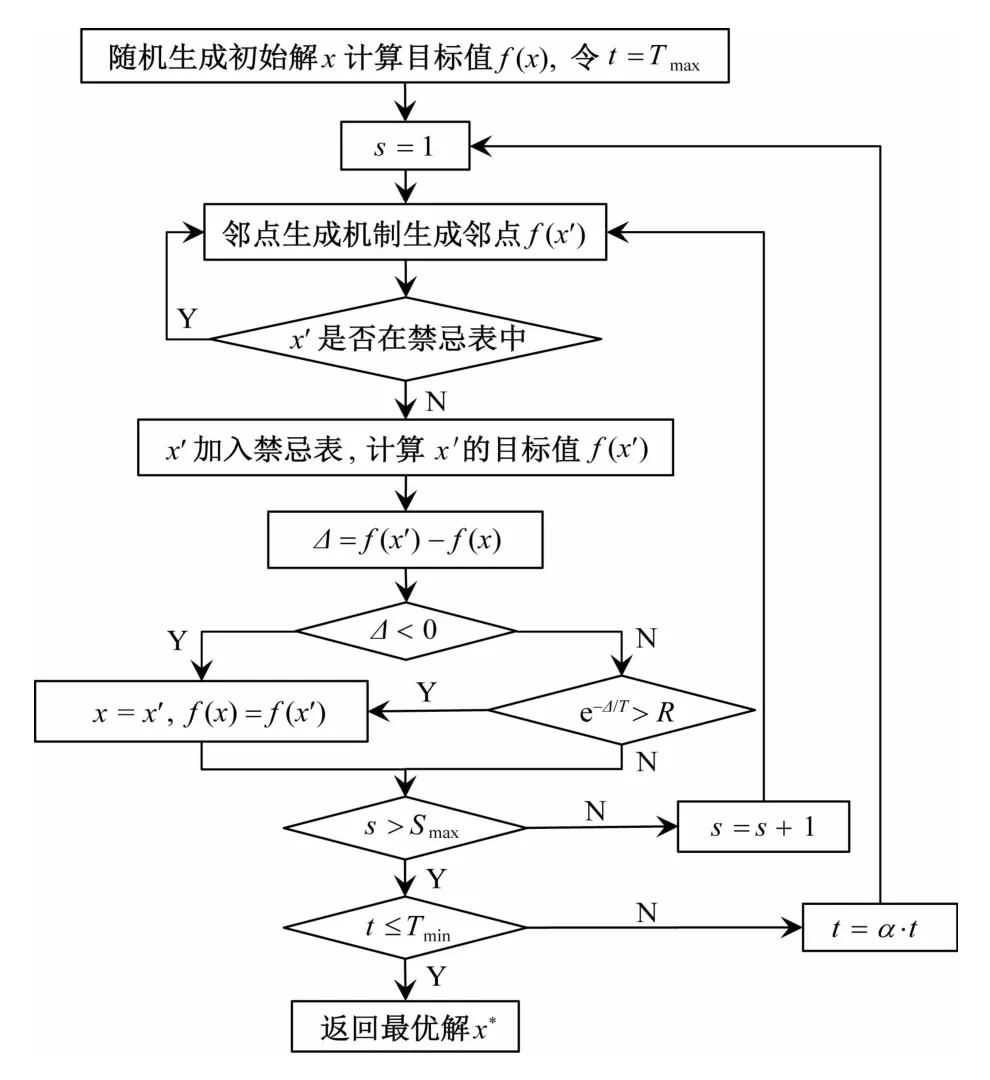
图2 TSA 流程图
启发式算法的关键在于如何将多重空间干涉约束反映到TSA 的内核——调度生成机制(Schedule Generation Scheme,SGS)上,即将AL解码为一个满足时间和空间约束的调度方案。本文设计的SGS基于传统的串行调度生成机制(SSS)创新性地融入多重空间干涉的约束条件。
为方便计算机处理,首先将空间网格化(离散化),设网格粒度Δ= (δx,δy,δz)。工程现场的整体空间被划分为K个网格,每个网格空间大小相同,体积为δx·δy·δz。基于网格化空间,定义已知参数和 变 量。定 义0/1 参 数∀i∈N,k∈K表示活动i的空间占用情况。=1表示活动i的第h类空间需求包含网格k,h∈{S,G,T,R,W,B};反之为0。定义0/1变量,∀k∈K,t∈T表示在t时间段的网格空间k的占用情况。=1表示空间网格k在第t时段被h类需求空间占用;反之为0。网格化后,空间体积的计算表示为占用的网格体积求和。
基于网格化空间,SGS算法伪代码如下:
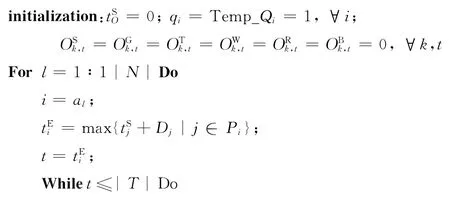

SGS根据AL中的活动顺序依次安排每个活动的开始时间,活动开始时间是满足各约束条件(工序约束、空间冲突约束、质量约束)下的最早开始时间。具体地,针对任意活动i,工序约束要求活动i的最早开始时间应不早于其紧前活动的最晚结束时间,活动i的最早开始时间Pi}。初始化令活动i的开始时间为t iE,接着进行循环操作,判断空间冲突约束和质量约束是否都满足。若约束满足,则当前时间是活动i的开始时间;否则,令活动i的开始时间延迟一单位时间,继续判断约束条件是否满足。依次循环,直至找到满足所有约束的开始时间。针对空间冲突约束,不等式组(7)计算各类空间重叠的体积,进而判断是否存在安全威胁、物理冲突和破坏冲突。其中,“or”条件表示当不等式组中任意一个公式成立,空间冲突发生。针对质量约束,式(8)、(9)计算当前活动与已安排的活动之间弹性空间干涉(拥堵)影响下的质量因子。若质量因子大于下限,则说明拥堵在可接受范围内,分配当前时间为活动的开始时间;否则,不可接受,需将活动开始时间延迟一单位时间,继续上述判断,直至质量约束满足。由于有限的时间延迟操作能减少或避免活动时间重叠,从而减少或避免空间干涉,故SGS可以在有限次迭代中产生满足空间干涉约束的调度方案。当所有活动的开始时间确定,得到一个满足所有约束的活动调度方案,SGS算法结束。
4 计算实验与结果分析
4.1 实际案例分析
基于文献[6]中的真实案例,本文设计的工程案例是一个由9个活动构成的建设项目,各活动基本信息如表1 所示。根据表1,加上虚拟开始节点0和结束节点10,项目的AON 项目网络如图3所示。设置网格粒度Δ= (0.5,0.5,0.5),各个活动的空间需求可视化表示如图4所示。例如,活动3、4、5搭建的脚手架需要临时空间的最小顶点位置为(0,-3.5,0),最大顶点位置为(40,-1.5,9),空间体积为720 m3。其他已知参数以及TSA 算法的参数按表2设置,其中,函数⎿⏋表示向下取整。

表1 活动信息表

图3 AON 网络

图4 三维空间需求
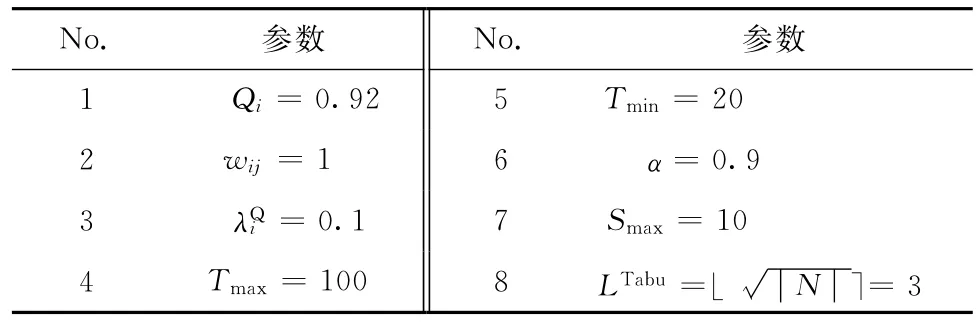
表2 参数设置
执行TSA 算法求解算例,算法在软件MATLAB R2013a上编译,算例实验在CPU 主频2.53GHz、内存2GB、32位操作系统配置的个人计算机上运行实现。仅耗时164.73 s,迭代收敛生成最优调度方案的总工期fMS=15。最优调度方案具体表示为甘特图,如图5所示。由图5可以看出,该调度方案避免了活动6 产生的安全威胁以及活动3、4、5与其他活动可能发生的物理冲突。活动7、8的弹性空间在时间段(2,4]上相互干涉,但只是产生轻微拥堵,活动7、8 的拥堵对活动质量的影响被控制在小于0.02的范围内,活动7、8的质量因子分别是0.983 3和0.999 7,均大于0.98,其他活动质量因子均为1。该方案不仅满足活动工序约束,还避免了空间冲突的发生并控制拥堵在可接受的范围内。

图5 最优调度方案甘特图
4.2 随机算例实验分析
随机生成一组算例,算例规模分别为10、20、30、40、50,每个规模下随机生成5个算例数据,包括项目计划网络以及每个活动的各类空间需求。不妨将每个算例命名为Js-n,其中,s为规模,n为算例编号。例如,J30-2表示规模30的第2个算例。其他已知参数的随机生成规则为:

其中,函数U表示均匀分布。TSA 算法参数设置如表3所示,并令=0.95。

表3 质量下限影响分析
为了验证算法的有效性,采用本文提出的方法(考虑空间干涉)和传统调度方法(不考虑空间干涉)求解算例问题。统计各问题规模下的平均工期和平均质量,如图6所示。由图6可以看出,两种方法求解出最优方案的工期基本相同,但考虑空间干涉的最优方案的平均质量更高。这说明,用本文提出的方法求解的调度方案在确保工期最小的情况下,资源拥堵程度更低。事实上,除了算例J40-4之外的其他所有算例,两方法得到的最优工期均相同。即便对于算例J40-4,不考虑空间干涉的最优工期为38,考虑空间干涉的最优工期为39,仅仅延长了一个单位时间。

图6不考虑和考虑空间干涉工程调度工期和质量对比图
图7所示为不考虑空间干涉约束时最优调度方案的各类空间冲突和总空间冲突水平。由图7可以看出,不考虑空间干涉时,调度方案容易产生空间冲突,并且空间冲突水平随着算例规模的增大而增大。相比之下,本文设计的方法在解码SGS 流程中已经避免了空间冲突,3类空间冲突水平和总空间冲突水平均为0。

图7 不考虑空间干涉时的各类空间冲突
以J50-1为例,研究质量下限Qi对结果的影响。保持其他参数取值不变,设置Qi取值分别为1,0.9,…,0.5。每组参数做3次实验,统计结果见表3。可以看出,随着质量因子下限的不断降低,最优调度方案的总工期逐渐缩短(由79逐渐降至68)。这是因为,当Qi降低,算法允许活动间存在更大程度的拥挤,活动并行的时间增加,故总工期得以压缩。但是总工期对参数改变的灵敏度不同,在[0.8,1]区间内,Qi每降低0.1,总工期下降3~4个时间单位;而在[0.5,0.7]区间内,Qi每降低0.1,总工期只下降了一个时间单位,工期的压缩幅度随Qi的下降呈现逐渐减缓的趋势。此外,随着参数值下降,算法耗时也逐渐减少。这是因为Qi越低,质量约束越容易满足,解码算子(SGS)中的循环次数减少,从而解码速度得以提高。最优方案的平均质量因子和最低质量因子值随着Qi的降低均逐渐下降,但确保活动质量大于等于Qi。
综上分析,本文设计的方法能有效避免安全威胁、物理冲突和破坏冲突等3类空间冲突,有效控制拥堵,将拥堵对活动质量的影响控制在可接受的范围之内,并且尽可能地缩短总工期。本文提出的方法能有效地保证工程调度的效率和质量。
5 结语
在工程实践中,减少活动之间的空间干涉是保障工程进度和质量的重要措施。研究带有多重空间干涉的工程调度优化问题,创新性地将空间从多个角度分类并定义了4类空间干涉。建立考虑多重空间干涉约束的工程调度数学规划模型,设计应对该问题的TSA启发式算法,尤其是在SGS的设计中融入了多重空间干涉约束条件。例举一个工程实例和随机生成的算例群进行计算实验,结果表明,TSA 生成的最优工程调度计划方案能有效地避免安全威胁、物理冲突和破坏冲突3类空间冲突发生,控制拥堵在一定范围内并尽可能地缩短项目工期。本文研究的问题、模型及算法可依据具体的工程特点,自定义空间需求、干涉约束和质量影响函数,具有一定的普适性和可扩展性,为工程管理者提供决策支持。未来可以在空间需求的动态性特征、空间干涉对作业效率的影响以及算法性能提升等方面做进一步研究。
