基于突变理论的海上运输关键节点脆弱性度量

李晶，李宝德，王爽

（大连海事大学 交通运输管理学院，辽宁 大连 116026）

海上运输节点是船舶在海上航行时经过的具有特殊地理位置或特殊供给功能的特定海上区域，主要包括运河、海峡以及重要港口。海上运输节点脆弱性是指当这些节点受到恶劣天气、海盗、海上恐怖主义等随机因素影响时抵抗灾害的能力。关键节点是海上运输网路形成的重要基础和支撑，因此，分析海上运输关键节点的脆弱性对海上运输的顺利进行具有重要的意义。

脆弱性的概念最早是在自然灾害问题研究中提出的，当前较为广泛应用到基础设施等网络安全的研究中。张超等[1]对关联基础设施网络的脆弱性进行了研究，通过仿真实验分析了关联关系对脆弱性的影响；在航运网络安全研究中，Berle等[2]针对海上运输系统脆弱性研究没有考虑不可见因素影响的缺陷，提出了结构性综合脆弱性评价方法对其进行分析；Berle等[3]对于海上运输系统发生中断的后果进行分析，并分析如何减少这种后果；陈鑫[4]采用贝叶斯网络识别出我国海上运输的关键节点，进而对于网络整体的脆弱性进行了分析。

随着海上非传统安全问题凸显，海上运输关键节点安全性的研究日益得到重视。Lee等[5]针对马六甲海峡海盗问题，提出了马来西亚、新加坡和印度尼西亚三国的制度和管理标准需要合作制定的建议。Rusli[6]分析了马六甲海峡的重要性和安全性，探讨了是否应该将马六甲海峡设定为特殊敏感海域；Bonney[7]、El-Eraki等[8]以及Pham[9]分别针对巴拿马运河、苏伊士运河和霍尔木兹海峡的不同方面进行了安全状况分析；吕靖等[10]采用投影寻踪法对我国海上运输关键节点的安全进行了评价。

在以往的研究中，突变理论被应用在有形和无形网络脆弱性评价中。Zhang等[11]采用突变理论对我国4 个区域的信息化水平进行了评估；Sadeghfam 等[12]采用基于多目标评估系统的突变理论法对地下水的脆弱性进行分析；牛志广等[13]针对突发事件对城市配水系统的作用，基于突变理论提出一种新的配水系统脆弱性评价模型；齐迹等[14]将模糊突变原理应用于海上交通风险领域，在构建海上交通风险评价指标体系的基础上，建立了基于模糊突变的海上交通风险综合评价模型；朱乐群等[15]将突变理论进行了推广，采用高维的突变级数法对海上通道的突发事件进行预警分析。

考虑到海上运输节点在运输中的重要作用，本文对海上运输关键节点的脆弱性展开研究。在前人研究的基础上，对传统的突变模型加以改进，构建海上运输节点脆弱性评价模型，以及海上运输关键节点脆弱性评价指标体系。进而，根据我国不同重要物资运输航线所经过的海峡及运河，遴选出我国海上运输关键节点，以此为研究对象进行实证研究。

1 海上运输关键节点脆弱性突变模型构建

1.1 海上运输节点脆弱性特征

海上运输节点安全受到来自外部的各种不确定因素影响，但在各种安全措施的保障下，一段时间内这些威胁因素与节点自身的防御能力之间会处于一种相对静止状态，此时运输节点处于一种稳定的均衡状态。而当某个时间点上，新的安全威胁出现或原有安全威胁影响程度发生改变时，节点原有的均衡状态有可能被打破，运输节点的安全状态发生了突变。因此，海上运输节点处于何种安全威胁之下，且抵御外部安全威胁从而维持其原有均衡状态的能力，综合反映了海上运输节点的脆弱性状况。分析海上运输节点脆弱性，发现其具有如下特征：

（1）海上运输节点的脆弱性受到来自外部的灾害因素和应对灾害的各种措施两类控制变量相互耦合作用的影响。

（2）海上运输关键节点稳定状态在上述两类控制变量的影响下会发生突然改变，通过度量海上运输节点安全的突变状态可以有效评价海上运输节点脆弱性。

（3）在海上运输节点安全威胁发生突变前后会出现两个稳定状态。

1.2 突变模型原理

突变理论是由Thom[16]基于拓扑学、结构稳定性等数学基础提出的，用来解决非连续变化和突变现象的理论。基于突变理论的突变模型由势函数来描述，势函数由状态变量和控制变量来确定，其中，状态变量表示系统的行为状态，控制变量表示影响状态变量的各种因素。设f（x，c）为系统的势函数，其中，x为状态变量，c为控制变量。则临界点方程为

式（1）是一个平衡曲面，由全部临界点组成，在退化的临界点附近系统处于不稳定状态，如果控制变量稍微变动，则有可能导致系统发生突变。而退化的临界点满足如下条件：

通过消除式（2）中的x得到分歧点集方程，分歧点集方程则是所有势函数形式发生变化点的全体。通过分歧点集方程可以推导出归一化公式，归一化公式是将系统各控制变量的不同质态归一化为可以比较的同一种质态，从而对系统进行量化递归运算。求出表征系统状态的系统总突变隶属函数值，以此作为综合度量的依据。

Thom[16]证明，任何动态系统，如果控制变量c中的元素不超过4个，则系统势函数最多只有7种突变形式，其中状态变量为一维的势函数及对应的归一化公式如表1所示。

1.3 模型构建及度量方法改进

1.3.1模型的构建 一般而言，突变现象具有多态性、突变性、不可达性、磁滞性和发散性的特质。在社会科学领域，如果具备上述两个以上的突变特质就可以考虑使用突变模型进行分析[17]。而海上运输节点脆弱性突变特征具备突变现象的特质，采用突变模型可以有效描述海上运输节点从稳定均衡向非稳定状态变化的情况。设置关键节点脆弱性势函数为V（x，c），其中，x为状态变量，c为控制变量。即状态变量为关键节点的脆弱性大小；控制变量为各种影响因素，共同作用决定了关键节点的脆弱性。关键节点的脆弱性状态及判断标准为：

表1 系统函数突变形式

式（3）为关键节点的脆弱性势函数；式（4）为关键节点在状态空间的平衡曲面，该曲面表示关键节点自身所受脆弱性因素作用达到了平衡；式（5）是分歧点集方程，可以判断关键节点脆弱性是否处于稳定状态。当Δ＜0时，表示关键节点脆弱性处于不稳定状态；当Δ=0时，表示关键节点脆弱性处于临界稳定状态，即使是微小的干扰也可能造成关键节点的脆弱性的突变；当Δ＞0时，表示关键节点脆弱性处于稳定状态。具体的度量步骤包括指标的递阶层次结构的构建、各个指标体系突变模型的确立、根据分歧点集方程推出归一化公式以及对结果进行分析计算等。

1.3.2度量方法的改进 以往研究大多采用定性方法建立递阶层次结构，本文考虑建立的递阶层次结构要考虑因素之间的重要性状况，而海上运输关键节点脆弱性指标之间代表性程度不同，指标之间会存在信息重复性问题。因此，为了使脆弱性指标能够综合度量各个运输节点的脆弱性和客观的说明因素之间的重要程度，本文采用因子分析法建立关键节点的递阶层次结构，使之更具有客观性和代表性。

首先，由于原始数据取值范围和度量单位各不相同，故要将指标数据规范化，本文采取规范化的公式，即正向指标和逆向指标：

式中：为影响因素处理后的值；x ij为第i个关键节点的第j个影响因素；i= （1，2，…，n）为关键节点；j= （1，2，…，m）为 影 响 因 素；max（x ij）和min（x ij）分别为第j个影响因素的最大值与最小值。

其次，影响因素因子关系表达式可以描述为：

式中：x1，x2，…，x m为标准化后的影响因素变量；F1，F2，…，Fρ为ρ个因子变量；aij（i=1，2，…，m，j=1，2，…，ρ，ρ≤m）为因子载荷。由式（8）的关系表达式，首先计算因素指标的相关性矩阵，根据相关性矩阵计算的累计方差贡献率可以确立选取的因子指标；然后计算因子载荷矩阵可以确立指标的关系和重要程度，最终可以建立因素指标的递阶层次结构。

在采用突变级数法计算时，得到的值通常具有聚集性，为了使计算的脆弱性指标值更加直观地表示关键节点脆弱性之间的关系和有利于后续操作，依据参考文献[18]，对传统突变级数法计算得到的初始脆弱性综合值进行了改进：

（1）根据关键节点的脆弱性突变模型，计算最底层控制变量均为｛0，0.2，0.4，0.6，0.8，1｝的综合突变值ri，并将这6个值作为刻画初始综合值的等级刻度，不同等级水平的相应区间为[ri，ri+1]，i=0，1，…，4。

（2）将计算得到的脆弱性指数综合值Rj｛R1，R2，…，Rn｝（n为关键节点），根据其落入的等级刻度区间[ri，ri+1]，i=0，1，…，4，将其映射到对应的区间中，得到调整的脆弱性指数的综合值为｝，则

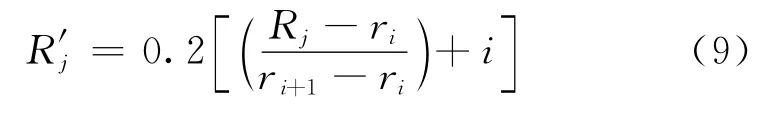
2 海上运输关键节点脆弱性指标体系构建

2.1 影响因素

根据海上运输节点脆弱性的特征可以看出，海上运输关键节点的脆弱性是海上运输关键节点受到一些不利因素影响时的一种抗灾能力，这种抗灾能力一方面取决于灾害的影响程度，另一方面取决于应对灾害的能力。

当前影响海上运输关键节点通过状况的因素主要有传统和非传统威胁两大类。冷战结束后，传统军事对抗对海上运输节点威胁有所减弱，但部分地区内部的军事冲突、海上强国对关键运输节点的军事控制仍然对海上运输节点的通过状况形成重要威胁。除此之外，台风、大雾、浮冰等极端天气的影响，还有大浪、地震、海啸等自然因素，以及近年来海盗、海上恐怖主义等威胁因素对关键节点的脆弱性影响也日趋严重，比较严重的地区像亚丁湾、马六甲海峡等区域。

从海上运输关键节点应对灾害能力方面而言，关键节点所属国及使用国的法律政策、国际合作以及有关国际组织出台的政策协定等都是影响海上运输关键节点保障能力的重要因素。目前，各个关键节点所属国或相关国际组织均积极采取各种措施降低海上运输关键节点的脆弱性。例如，通过各种法律政策、设立专门机构来保障关键节点、加强不同国家之间的合作等。

2.2 指标体系构建

本文将影响海上运输关键节点脆弱性的两类因素作为评价海上运输关键节点脆弱性的一级指标，其中：将表示海上运输灾害性程度的指标称为海上运输关键节点易损性，反映的是系统对外部干扰易于感受的性质，主要取决于系统结构的稳定性；将海上运输关键节点保障能力指标称为海上运输关键节点适应性，是系统对灾害事件的响应与应对能力，以及从灾害损失中的恢复能力，反映了系统可避免损害的程度，决定了系统在灾害事件影响下的实际损失大小。二级指标具体如表2所示，二级指标会随着时间和程度的不同发生变化。其中，易损性二级指标为逆向指标，适应性二级指标为正向指标。

表2 脆弱性指标体系

3 我国海上运输关键节点脆弱性实证分析

3.1 关键节点选取

根据我国不同货物运输航线所经过的重要海峡及运河，以及在该海峡或运河的重要作用，归纳出如表3所示海峡及运河作为我国海上运输的关键节点。

3.2 关键节点脆弱性度量

3.2.1数据来源及规范化处理本文数据主要来自于IBM 的GISIS数据库，其中海盗和事故数量是从2010～2015年统计和筛选出的数据；另外，从劳氏市场协会、FP Marine Risks和一些国家的海事机构网站搜集整理了相关指标数据。运用式（6）、（7）对我国海上运输关键节点各项指标数据进行规范化处理，结果如表4所示。

3.2.2关键节点递阶层次结构建立通过因子分析，前4个因子对我国海上运输关键节点各指标的累计解释率达到88.396，保留前4个因子，计算其因子载荷矩阵如表5所示。

由因子载荷矩阵可以看出，因子1在国际合作、海盗的载荷到达90%以上，事故数量和法律政策因子载荷也比较高，所以，因子1表示受到海盗和事故等对于我国运输关键节点的脆弱性的影响；因子2在军事冲突和军事基地的载荷较高，故因子2表示军事方面对于我国海上运输关键节点的脆弱性的影响；因子3在可替代性和海上恐怖主义的载荷较高，故因子3表示海上恐怖主义、可替代性对于我国海上运输关键节点的脆弱性的影响；因子4在保证性规范和相关组织机构方面的载荷较高，故因子4表示保障性方面对于我国海上运输关键节点脆弱性的影响。

进而建立图1的递阶层次结构模型。其中，每一层从左到右的重要性逐渐减小。

表3 我国海上运输关键节点

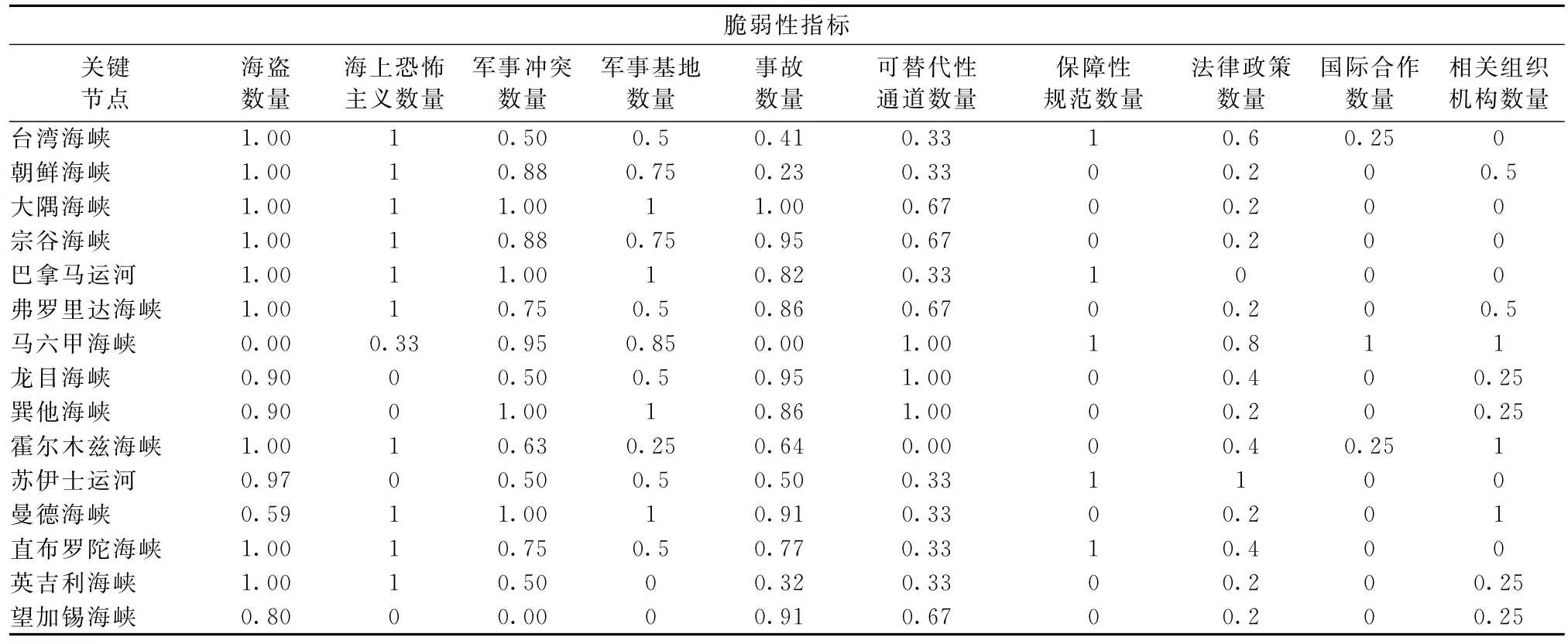
表4 我国海上运输关键节点规范化数据

表5 因子载荷矩阵

3.2.3关键节点递阶层次结构突变模型的确立根据递阶层次结构分析，可以确立如图2所示的我国海上运输关键节点脆弱性突变结构模型。

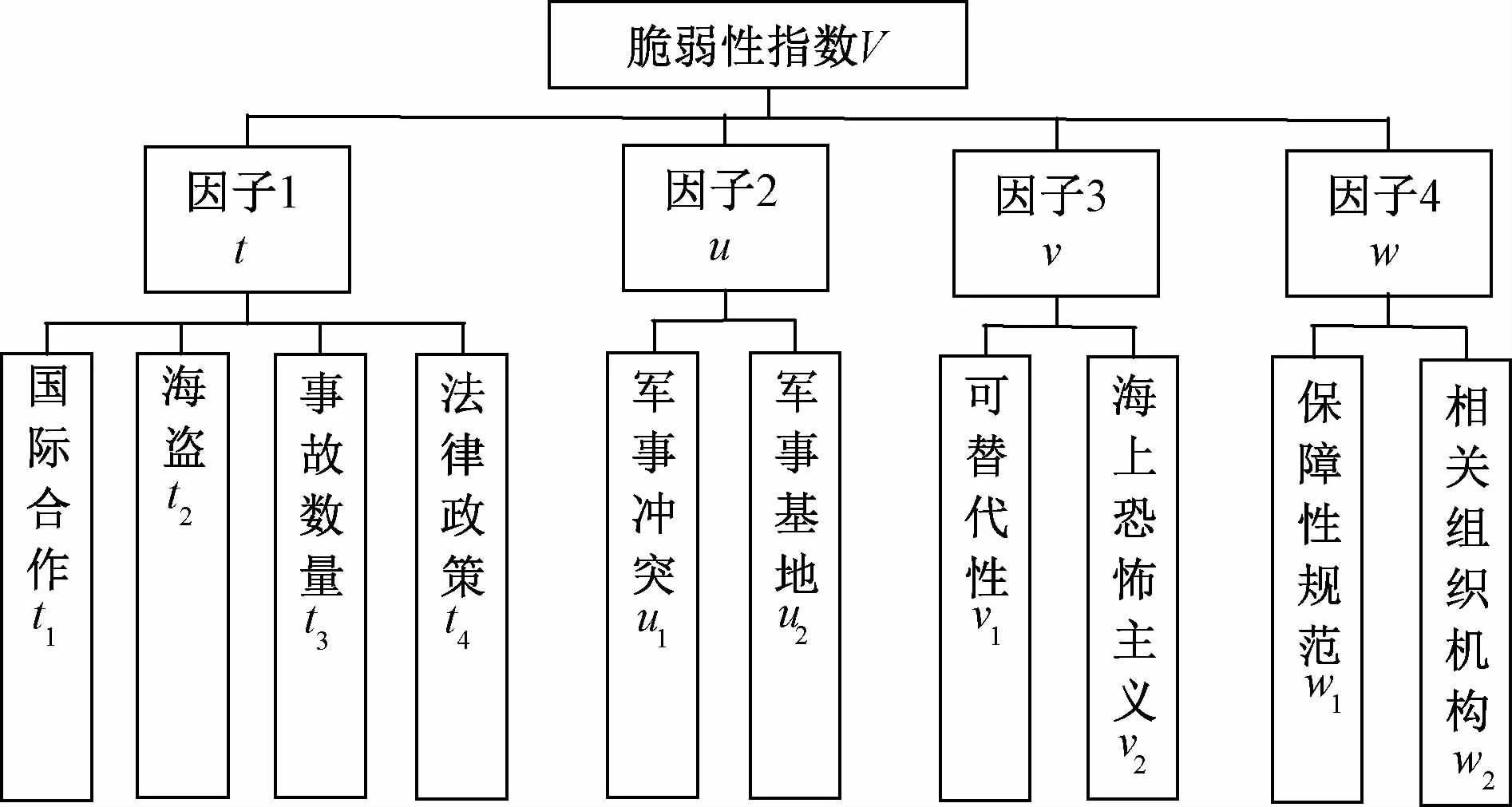
图1 脆弱性度量指标的递阶层次结构图

3.3 结果及分析

3.3.1度量结果根据改进的脆弱性等级计算方法，将我国海上运输关键节点脆弱性等级划分为5级，计算得到关键节点脆弱性等级刻度如表6所示。由于计算结果中脆弱性指数越大表示脆弱性越低，故1级表示脆弱性最高，5级表示脆弱性最低；而较低的脆弱性表示较高的抗灾能力。因此，1～5级脆弱性对应的抗灾能力分为很低、低、中、高和很高5个等级。

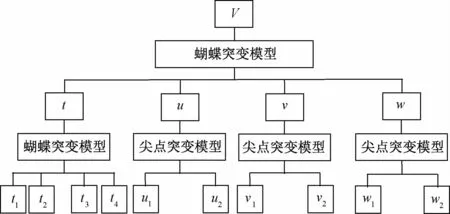
图2 关键节点脆弱性突变模型

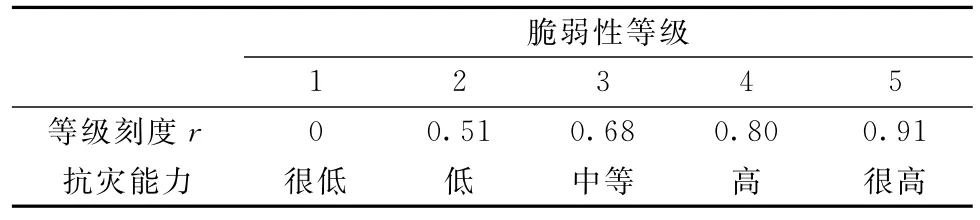
表6 关键节点脆弱性等级刻度表

计算得到的脆弱性指数值、调整的脆弱性指数值和排序如表7所示，其中脆弱性指数值越大，脆弱性越低；因子1～4对于我国海上运输关键节点的脆弱性影响的计算结果如表8所示，其中脆弱性指数值越大，脆弱性越低。

表7 我国海上运输关键节点脆弱性度量结果

3.3.2脆弱性度量结果分析综合来看，我国海上运输关键节点脆弱性状况如图3所示。由图3可以看出，我国海上运输关键节点的脆弱性大部分处于高、中、低3个区间内，其中望加锡海峡脆弱性最高，脆弱性最低的是台湾海峡，并且同一等级的脆弱性相差不大，但是由于本文考虑的是随机因素，故影响脆弱性的因素会随时发生变化。因此，即使脆弱性相差不大，但某一方面的影响因素突然变化也可能造成脆弱性的迅速改变，所以要针对影响关键节点脆弱性的具体不同方面，加强应对的措施。

表8 因子1～4对脆弱性的影响度量结果

脆弱性最低的台湾海峡，从具体影响因素来看，在4个因子中，因子1和因子2，即国际合作、海盗、事故的发生、法律政策、军事冲突和军事基地，对于台湾海峡脆弱性的影响较小。通过分析原始数据可以看出，台湾海峡脆弱性的影响主要来自于天气等因素导致的事故的发生，但台湾海峡整体脆弱性较低，可以看出，目前台湾海峡针对事故发生所进行的保障较多。相对于因子1和2、因子3和4，即可替代性、海上恐怖主义、保障性规范和相关组织机构，对台湾海峡的影响较大。因子3和4主要是适应性指标，所以保障能力是台湾海峡安全的关键，应继续加强与完善相关保障措施。此外，曼德海峡、直布罗陀海峡、弗罗里达海峡、苏伊士运河以及朝鲜海峡的脆弱性也相对较低。

脆弱性最高的望加锡海峡，深入分析可知，易损性指标方面对望加锡海峡的脆弱性影响较大，而适应性指标方面对其影响相对较小，所以综合促成望加锡海峡整体的脆弱性较高。从具体影响因素来看，因子1和4对望加锡海峡的脆弱性较小，因子2和3对其脆弱性影响较大。并且与其他关键节点相比，因子2和3对望加锡海峡脆弱性影响是最大的，即军事冲突、军事基地、海上恐怖主义和可替代性对其影响明显，所以应加强对这些方面的防范。

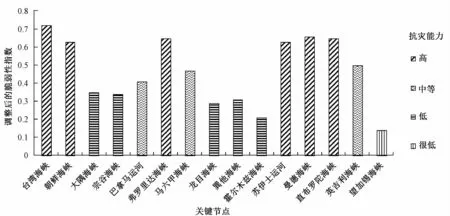
图3 我国海上运输关键节点脆弱性综合度量结果

作为连接太平洋与印度洋的咽喉要道，我国重要货物运输的通道，马六甲海峡的脆弱性相对于其他关键节点的脆弱性则处于中间位置。由表8可以看出，因子4，即保障性规范和相关组织机构方面，对于马六甲海峡脆弱性影响较小，并且相对于其他关键节点，因子4对马六甲海峡脆弱性影响也是比较小的。说明马六甲海峡在脆弱性适应方面目前做得比较好。但是，作为马六甲海峡的替代通道龙目海峡和巽他海峡的脆弱性相对较低，所以马六甲海峡还要在适应性方面不断加强。同时，脆弱性处在中间的还有英吉利海峡、巴拿马运河以及霍尔木兹海峡等。

单从4个因子对关键节点的脆弱性影响来看，因子1对马六甲海峡和巴拿马运河的脆弱性影响最大，对霍尔木兹海峡的脆弱性影响最小；因子2对望加锡海峡的脆弱性影响最大，对大隅海峡、巴拿马运河、巽他海峡和曼德海峡的脆弱性影响最小；因子3对龙目海峡、巽他海峡、霍尔木兹海峡和望加锡海峡的脆弱性影响最大，对大隅海峡、宗谷海峡和弗罗里达海峡的脆弱性影响最小；因子4对大隅海峡和宗谷海峡的脆弱性影响最大，对马六甲海峡的脆弱性影响最小。因此，针对不同因素对关键节点的脆弱性影响大小，要采取相应的措施来进行防范。

4 结语

本文采用改进的突变模型对我国海上运输关键节点的脆弱性进行了度量，为更加准确地描述和分析海上运输关键节点的脆弱性提供了新思路。通过因子分析法定量的建立层次结构，不但避免了主观建立度量指标体系和确定影响因素重要程度的不准确性，而且更加准确地描述了实际问题。此外，对于计算结果还进行了改进，使结果的分析更加直观。结合具体实例的客观数据，进行了模拟验证。结果显示，脆弱性最低的是台湾海峡，最高的是望加锡海峡，而像我国重要的运输节点的马六甲海峡则处于中间位置；4个因子对不同的关键节点的脆弱性产生不同程度的影响。这些结果为我国21世纪海上丝绸之路的重新构建以及战略支点的打造具有重要意义，也为我国海上运输安全提出一些保障措施具有一定的参考意义。

本文基于对海上运输节点影响因素的理论分析得到海上运输节点的评价指标体系，今后可以考虑采用实证分析方法进一步筛选对海上运输节点脆弱性具有影响作用的指标。另外，本文采用改进的突变模型对海上运输节点脆弱性进行了静态评价，数据允许的情况下，可以进行动态评价，进而更加准确及时地把握我国海上运输关键节点脆弱性状况。