基于多目标演化算法的油田危险品物流系统选址-路径问题

杜天松 ，郭海湘，b，c ，潘雯雯，刘 晓

（中国地质大学a.经济管理学院；b.国土资源部国土资源战略研究重点实验室；c.中国矿产资源战略与政策研究中心，武汉 430074）

在物流系统优化方案中，选址和配送问题占有很重要的比重[1]，主要原因是选址问题是企业的中长期决策，作为物流系统优化的重要节点，仓储中心选址的好坏直接影响企业的服务质量、配送效率和运输成本，对企业物流发展具有重要的战略意义；而配送问题则是企业的中短期决策，运输成本已经占到物流总成本的70%[2]。因此，研究该问题对企业降低配送费用、提高利润和市场竞争力具有重要的战术参考价值。上述两个问题可以归纳为目前供应链与物流研究中的选址问题[3]和车辆路径问题[4]，早期的研究通常将两者分开单独研究，由物流实践中发现，选址问题和车辆路径问题在决策过程中具有内在关联性，即两者一般都要考虑物资集散中心和客户的分配关系、运输成本的最小化。因此，将两者集成研究，即选址-路径问题[5-7]对于设计最优的物流布局与布置配送路线具有重要的研究意义。

选址-路径问题（Location-Routing Problem，LRP）在近5年得到了迅速发展，主要研究方向有电子商务配送、军事基地构建[7]、应急物流[8-9]以及垃圾回收处理等[10-11]。从研究内容来看，目前专门从事选址-路径集成化物流视角来研究油气田、煤矿等能源企业物资配送问题[12-13]的文献较少，并且主要研究的是普通物资仓库的选址-路径问题，而对占油井年物资需求量达10%的危险品的存放仓库的选址-路径问题研究甚少。除此之外，目前的研究绝大多数假设仓库和需求点间是通过点对点的方式进行定点配送，该配送方式在需求物资同质化、需求点较少的物流网络中具有优化物流布局的积极作用。事实上，当前需求物资的多品种、小批量趋势日益明显，许多大型企业借鉴电商物流配送的经验，基于现有的配送设施，通过采取集中配送和定点配送相结合的方式，达到降低成本、增加效率的目的。例如，华北分公司——鄂南油田，随着该地勘探开发的不断深入，边缘井和单井数量日益增加，致使物资供应战线逐渐拉长，原有的定点配送和多库并存模式已经不能满足企业安全生产的要求，决策者考虑整合现有的危险品物资仓库、重构物流配送网络，以优化当前的物流网络布局。

鄂南油田位于甘陕交界地区，鄂尔多斯盆地南部，主要包括红河、洛河、泾河、渭北四大产油区块，2013年度鄂南油田年产油量5.45万t，是中国石油化工股份有限公司重要的石油产区之一。在当前的鄂南油田物资配送系统中，现有的7个县级危险品仓库为鄂南4个油田共584口开油井的生产提供化学药剂等物资。但是，随着该地勘探开发的不断深入，边缘井和单井数量日益增加，致使物资供应战线逐渐拉长，原有的定点配送和多库并存模式已经不能满足企业安全生产的要求，公司决定对现有的危险品物资仓库进行整合，并借此改进传统点对点的物资配送模式，亟待建立新的县级综合型物资仓库及配送网络，以优化当前的物流网络布局。公司经初步考察决定符合油田危险品物资仓库建库要求的县城共有18个，如图1所示；同时，各候选县城还要作为物资运往油井过程中的必经节点，负责对危险品运输车辆进行必要的安全检测和给养补充。

在物流网络布局优化决策中，已有文献主要是从服务质量、配送效率和运输成本等角度对网络布局的优劣进行分析[14-15]。张敏等[16]分析了在危险品物流网络中所需要考虑的优化目标，如运输成本、风险和风险公平性等；王海军等[17]利用机会约束方法，建立了在一定应急限制期下，时间最小化和成本最小化的双目标随机规划模型；Shang等18]对某制药工厂的选址进行了优化研究，主要考虑了运输成本和配送服务的可靠性等指标。基于上述分析，对于危险品物流网络而言，控制运输成本和减少风险是布局优化的重点，同时考虑到危险品物资在运输过程中易受外界条件的影响发生物化作用，若不及时运达，其利用价值会有所降低。因此，配送可靠性也是需要考虑的主要目标。

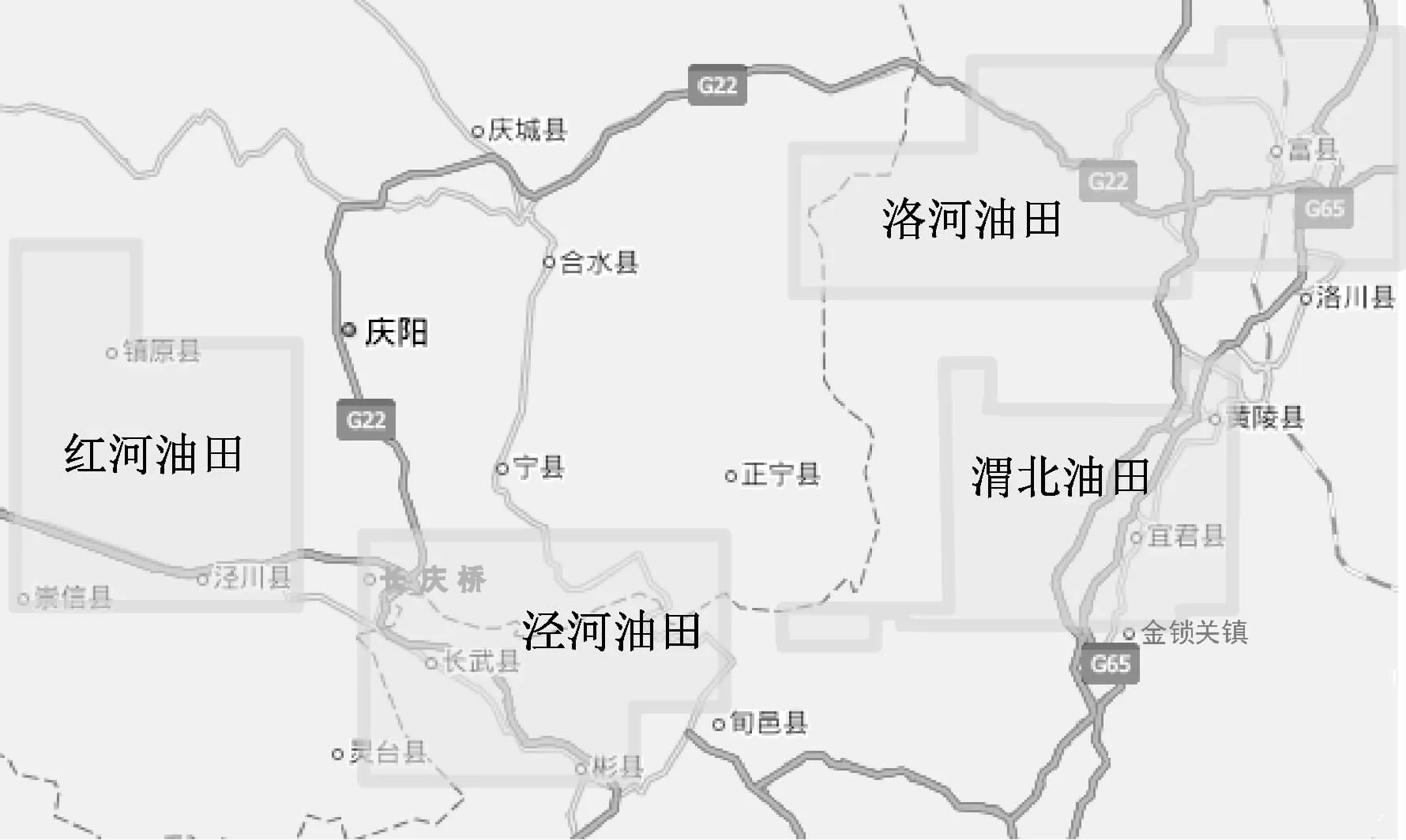
图1 鄂南油区危险品仓库候选点分布图

因此，本文提出了一个可以有效结合集中配送和定点配送的双层物流配送网络，从选址-路径集成化的角度，建立了一个总成本最小、风险最低、配送可靠性最强的油田危险品物资运输的多目标规划模型（Multi-ObjectiveLocation-Routing Problem of Oil-field Hazardous Material Transportation，MOLRPOHMT）。对于多目标优化问题的求解，Deb[19]提出Pareto最优解集合，并通过该集合找到最满意方案，Stummer等[20]针对医院选址问题，建立了多目标优化模型，通过采用禁忌搜索算法求得近 似Pareto最优解。因此，本文在求解MOLRPOHMT问题时，通过设计合理的编码和解码，将选址和路径问题集成优化，并结合多目标演化算法（Multi-ObjectiveEvolutionary Algorithms，MOEA）和Pareto的相关概念，通过合理地选择、交叉和变异策略，求得Pareto最优解集；在此基础上，本文引入随机多属性可接受度分析方法（Stochastic Multi-attribute Acceptability Analysis，SMAA）对Pareto最优解集进行再次筛选，求得最优选址方案和配送路线，具体研究思路如图2所示。

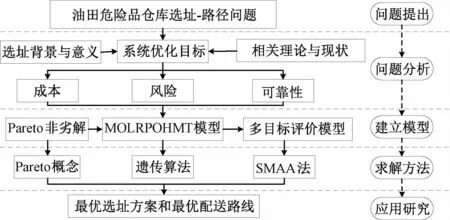
图2 研究思路

1 MOLRPOHMT模型

1.1 优化目标

（1）成本。成本是影响集成物流系统设计的一个重要因素。本文主要考虑新建危险品仓库的固定费用（包括土地租赁费用、建站费用及用于维护正常业务流程的运营费用等）、运输费用和因路网危险度瓶颈限制而带来的安全费用，文中将这3项成本之和最小化作为一个优化目标。

（2）风险。风险广泛存在于危险品物流系统中，人们希望危险品仓库和危险品配送路线离自己越远越好。一般而言，需要考虑两类风险：①存在于配送过程中的运输风险；②仓库选址时带来的选址风险。已有的风险表示方法有：传统风险、暴露人口数量风险、危险事件概率风险、感知风险和条件风险等[21-22]。本文采用暴露人口数量最小化作为优化目标。

（3）可靠性。油田危险品物资在运输过程中易受外界条件的影响发生物化作用，若不及时运达，其利用价值会有所降低。基于上述危险品物资时效性的特殊要求，本文将危险品物资送达所需时间的快慢作为评判标准来研究危险品物流配送系统的可靠性。

1.2 模型假设

为了更清晰地描述本文研究的问题，首先就路段和道路危险度等级做出如下说明：路段是指路网中任意两个节点间的通路。就本模型而言，车辆完成一次危险品物资的配送，需要从危险品仓库出发，途经多个中间节点，即通过多条路段后到达危险品物资需求点；而危险度等级是指在运输过程中因某些道路自身的因素（如路面平整度、安全防护程度和区域人员密度等）导致的道路危险性程度。在本模型中，路网中每个路段的危险度等级均不同，特别地，对于危险品仓库到任意需求点的任意一条通路而言，该通路中各路段的危险度中最高的那个危险度定义为该通路的危险度。由此可知，危险品物流网络中存在着危险度瓶颈限制：当配送车辆的安全配置等级高于或等于该路线的危险度等级时，就可安全地选用该路线；当配置低于该路线危险度等级时不能选用该路线，如果非要选择该路线，则必须将运输装备的安全配置增强到与之相匹配，配置的增强导致了总成本的增加。

其次，就鄂南油区配送模式做出如下说明：在传统物流配送模式中，鄂南油区首先是将分属于不同乡镇的油井物资需求进行整合，再通过由该县的危险品物资仓库安排相应车型的运输车辆，进而对各乡镇所需物资进行定点配送，这种单车场多车型的配送模式对沟壑纵横、地形高差较大的鄂南油区而言，既增加了运输成本，也增加了配送风险和配送时间。因此，有必要改进传统的物流配送模式，采用“油公司”管理模式下的双层配送网络去解决该选址-路径问题。该网络更多考虑了中途停靠节点在优化“多品种-小批量”物资配送网络的作用，中途停靠节点相当于虚拟车场，主要负责物资的再次调度转运，并且该点实现了集中配送和定点配送的有效结合：首先将各中途停靠节点下辖的油井所需危险品物资量进行整合，通过大运载车辆由危险品物资仓库以最为便捷的通道运往各中途停靠节点；进而，通过相应车型对需求进行分割，再由中途停靠点运往所辖区域内的油井，如图3所示，分别描述了危险品物资仓库和中途停靠点、中途停靠点和各井口之间的物资配送关系，而本文主要研究上层网络的仓库选址及车辆路径问题，并将中途停靠节点抽象为虚拟物资需求点，汇集了该点所辖区域各井口的物资需求。同时，考虑到各油井所在县城还要作为物资运往井位过程中的必经节点，负责危险品车辆的安全检测和给养补充。因此，在构建配送网络时，首先需要给出一定数量的县城作为建库候选点集合，并从建库候选点中选择确定数目的危险品仓库来服务油井，同时考虑将各县城作为物资需求点。该点既要对危险品运输车辆进行必要的安全检测和给养补充，又要负责所辖区域内的物资需求的再次转运。特别地，就建库选址点而言，它既是危险品仓库所在地，又是物资需求点。因此，物资流动所产生的成本、风险和时间可以忽略不计。

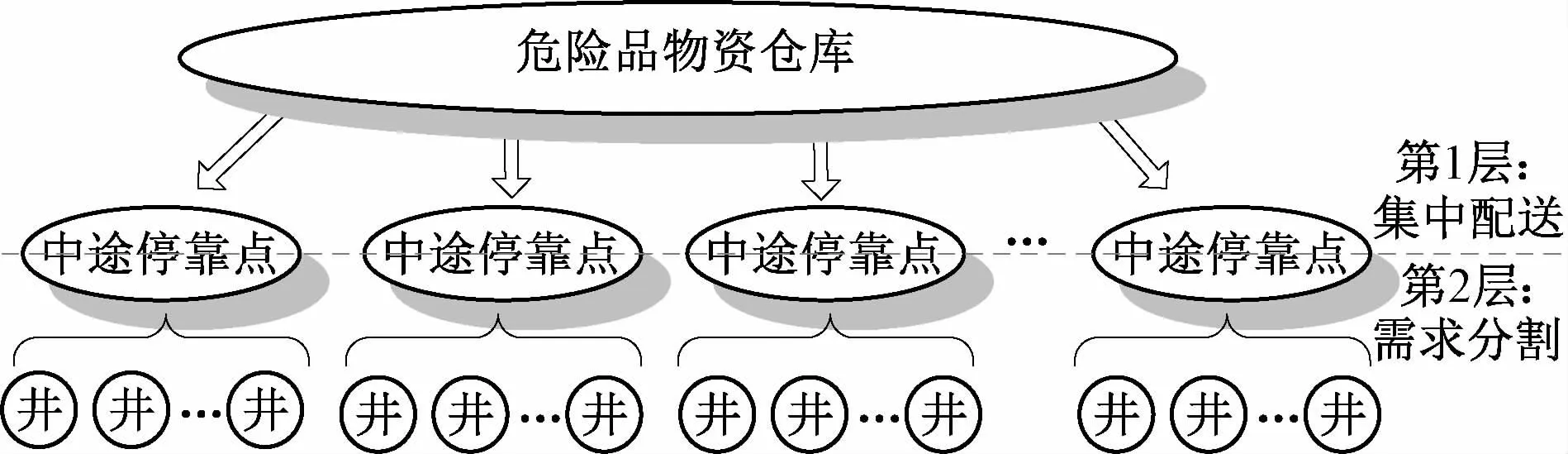
图3 鄂南油区危险品双层配送网络图

在明确上述定义的基础上，对本模型进行合理假设：

（1）建库候选点无容量和流量限制。

（2）每辆车最多服务一个物资需求点，且每个物资需求点只被一辆车服务。

（3）每个物资需求点选择由配送路线所含路段数较少的一个建库候选点提供服务。

（4）车辆有容量限制、但无数量限制，且不具备任何安全配置等级。

（5）如果某建库候选点被选中，则建立该危险仓库的固定费用已知。

（6）危险品仓库选址风险的危害半径已知，运输风险的危害半径已知，且到各需求点所需经过的各路段的驾车距离已知。

（7）各物资需求点的危险品物资需求量是确定的，并且在一定时期不变。

（8）配送网络需要的危险品仓库数量已知。

（9）路网中每个路段的危险度等级已知。

（10）各物资需求点所辖区域的井口数量、居民点人数和所辖区域面积已知。

油田危险品的独特性质使得危险品物流网络与其他产品的物流网络存在明显的区别，该网络的设计原则是在充分保证安全性的前提下兼顾经济性。为了保证安全性，避免服务仓库和车辆因容量和流量的限制而使得需求点不得不接受交叉服务带来的安全隐患，在配送网络设计阶段，决策者往往根据需要选择载重量较大的车辆，并及时扩建或新建仓库，从而保证假设（1）、（2）成立。假设（3）重点考虑路线的选择问题，路段数与各目标函数值成反比关系，即通常情况下，路段数越少的路径方案，其各目标函数值相对越优；但是由于路网中存在危险度瓶颈限制、运输风险和运输时间，致使在最少路段数下的路径方案不一定满足各目标函数值同时最优。因此，有必要将路线选择与危险品仓库选址集成求解，通过均衡各函数目标得到路网最优路径方案。假设（4）描述了运输车辆在安全配置方面参差不齐，既难以量化，又难以与道路危险度等级相对应。因此，假设各运输车辆均无安全配置等级，且以安全费用的形式代入成本函数中。即道路危险度等级越高，其成本越高，从而保证各运输车辆在克服危险度瓶颈限制的同时简化计算的目的。假设（5）～（10）是在符合实际情况的前提下为简化模型而做的一些假设。

1.3 参数和决策变量

G（M，N，P）是一个给定的路网图，如图4所示，M=｛I，F，B，Z｝为路网中有关危险品仓库和物资需求点的信息集合，首先需要在建库候选点集合I中选出一个作为建库选址点，即危险品仓库i（i∈I），而其他各点则被定义为物资需求点j（j≠i，j∈I）；F=｛fj|i∈I｝为建立危险品仓库的固定费用；

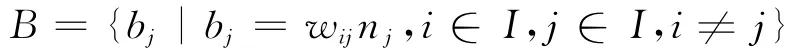
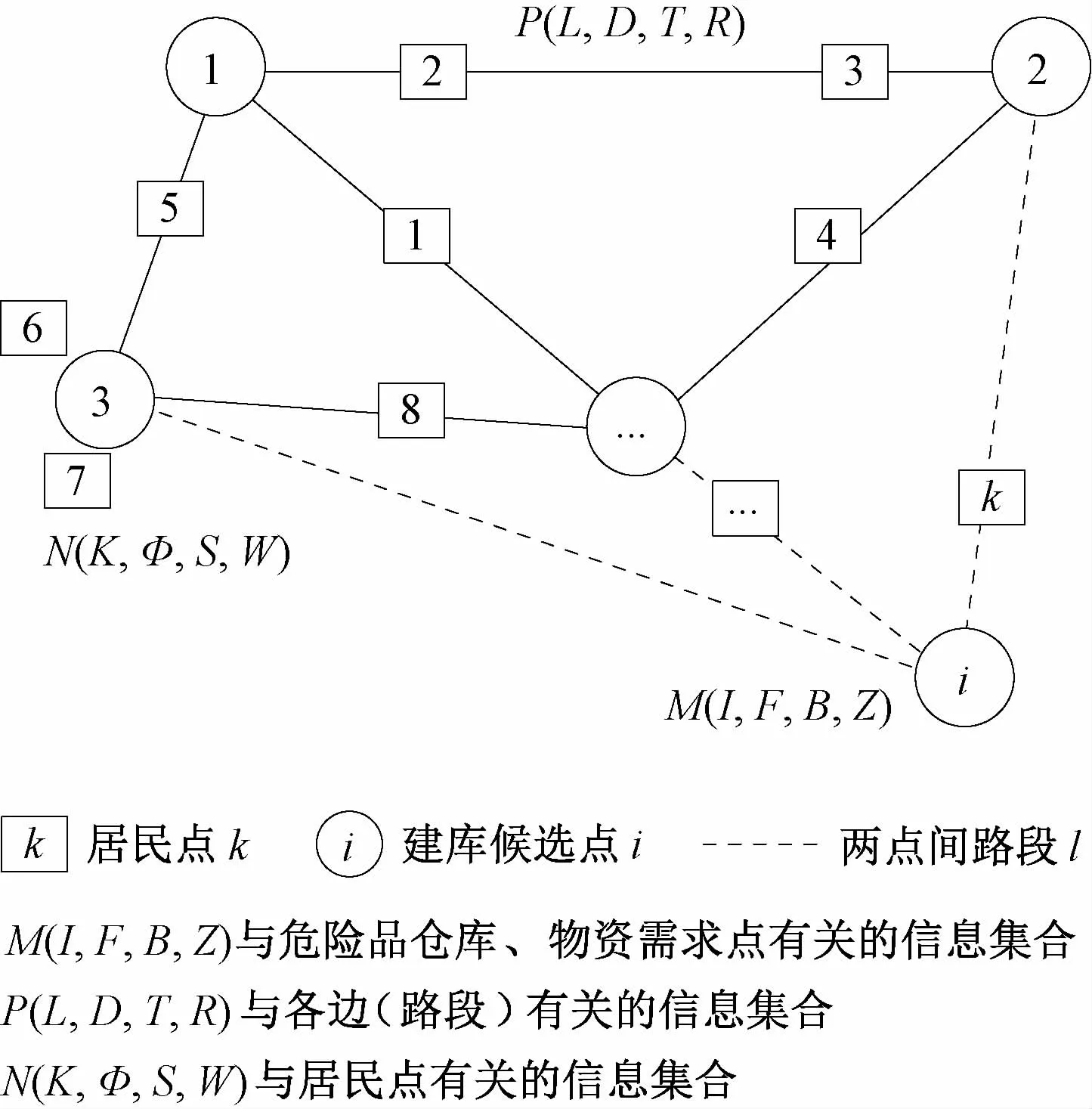
图4 基于MOLRPOHMT模型的路网图G（M，N，P）

为任意物资需求点的年危险品物资需求量集合，其中：w ij为危险品仓库i到物资需求点j单井危险品物资年配送量；nj为物资需求点j所辖区域内的油井数目；Z为危险品仓库和需求点下辖的危险品特种车辆类型，用z表示车辆类型，则每种类型车辆载重量为Qz（z∈Z）。N=｛K，φ，S，W｝为网络中所有受危险品物资存储、运输影响的居民点的信息集合；K为路网中所有居民点k（k∈K）的集合；

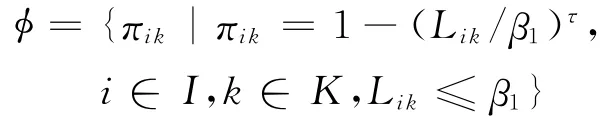
为事故发生时危险品仓库i对受影响居民点k产生危害的风险因子，其中Lik为危险品仓库i与居民点k之间的欧氏距离；β1为选址风险的危害半径，特别地，当Lik＞β1时，πik=0；幂指数τ的取值可根据实际情况确定，本文取τ=2。S=｛sk|k∈K｝为居民点k处所辖区域的面积；W=｛w k|k∈K｝为居民点k处的居民数。P=｛L，D，T，R｝为路网中与各边（路段）有关的信息集合；L为路网中所有路段l的集合；

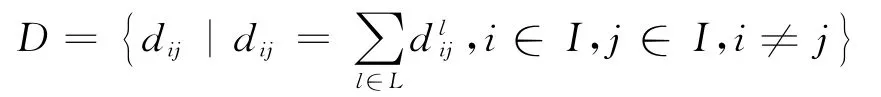
为从危险品仓库i到任意物资需求点j的网络最短路，其中为危险品仓库i到任意物资需求点j间所经过路段l的驾车最短路；

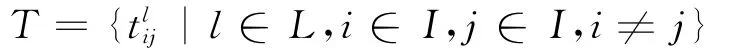
为危险品仓库i到任意物资需求点j间所经过路段l的时间；

为危险品仓库i到任意物资需求点j间所经过路段l的路网危险度等级。β2为运输风险的危害半径，即当居民点k离路段l的最短距离小于β2时，认为该居民点k在路段l上，并受到运输风险的威胁；V j为车辆从被服务的物资需求点j离开时车辆的剩余装载量；cij为危险品仓库i到物资需求点j的单位运输费用（单位：元/（t·km-1））；

为单辆车的安全费用，是一个可抵御最大危险度等级的非递减函数，其中：θ为常数；rij为从危险品仓库i到任意物资需求点j间该条通路的危险度等级，而该条通路的危险度等级一般定义为该通路中各路段的危险度中的最大值。

下面对模型中所涉及的决策变量进行简要介绍：

1.4 数学模型和约束条件

本模型综合考虑了成本、风险和可靠性3个目标，并从建库候选点中选出确定数目的危险品仓库来服务用户，并据此确定危险品仓库到任意需求点的配送路线，问题建模如下：

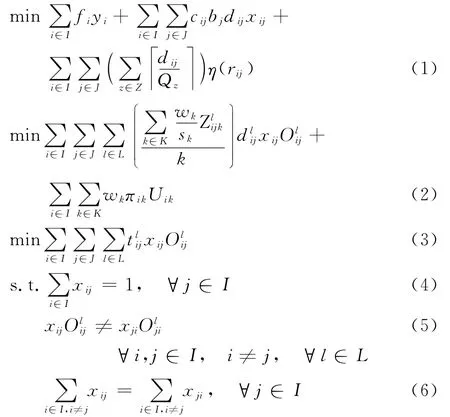
目标函数式（1）表示求最小化的建库费用、运输费用和安全费用之和；式（2）表示最小化的运输风险和选址风险之和；式（3）表示最小化的配送时间；约束条件式（4）确保每个物资需求点只被服务一次；式（5）保证每个路段不被重复遍历；式（6）表示每个物资需求点的车辆进出次数相等；式（7）表示车辆从物资需求点离开时的剩余装载量为0，即车辆一趟只服务一个物资需求点；式（8）确保物资需求点由已开设的危险品仓库负责配送物资；式（9）要求满足每个物资需求点所辖油井危险物资需求量；式（10）要求危险品仓库与任意需求点间的网络最短路由最少的子路段集成；式（11）表示候选点只能有一个被选中建库；式（12）～（16）表示决策变量的0-1整数约束。

2 多目标演化算法

基于多目标的选址-路径问题是NP难问题，传统的精确算法在解决该问题时，对需求点和设施的数目有严格的限制，尤其是当问题规模较大时，该算法存在一定的局限性。目前，以演化算法为主的启发式算法是解决NP难问题的常用方法，它主要是通过模拟生物界物种进化的过程来优化实际问题。演化算法种类繁多，模拟退火算法、差分演化算法、遗传算法等都属于此范畴，而本文选用遗传算法来求解选址-路径问题，主要是因为遗传算法在求解多目标优化问题时具备整数编码简单、全局搜索能力强、收敛速度快等优点[23]。

2.1 染色体的编码

染色体编码应满足完备性、非冗余性和易读性等原则。染色体采用实数编码，每个染色体分为两段，染色体子段1描述的是危险品仓库选址方案，在此假设有m个建库候选点，需要从这些候选点中随机选出1个作为建库的选址点，即危险品仓库i（i∈m），则其他各点被定义为危险品物资需求点j（j≠i，j∈m）；染色体子段2描述的是车辆路径方案，根据假设可知，有m-1个车辆路径方案，为便于研究，各路径方案的编码设计用车辆在危险品仓库i到需求点j间行驶所需经过的路段数n ij表示，符合该路段数的路径方案即为该条线路的车辆路径方案。染色体表示结构如图5所示。

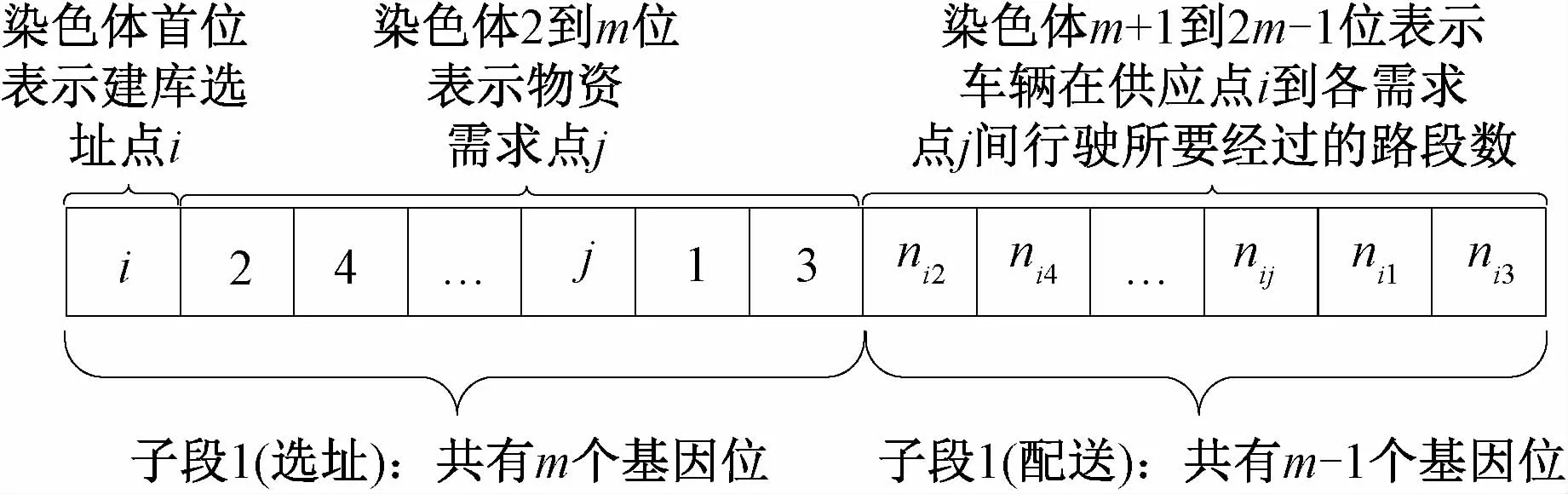
图5 多目标演化算法染色体结构图

图5中，染色体子段1有m位，是1～m的随机数排列，其中，首位表示建库选址点i，2～m位为物资需求点j；染色体子段2有m-1位，表示车辆在供应点i到需求点j间行驶所需经过的路段数，特别地，该路段数nij由介于两点间最少路段数min_nij和m-1段的一个整数集合

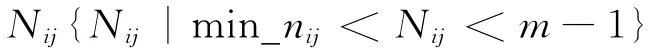
随机产生。该随机产生过程对解的有效性影响较大，同时考虑到假设（3）的成立，本文引入了泊松分布概率模型，对其随机产生过程进行干预，达到提高初始种群的质量、改进目标函数值的目的。

为了更清晰地描述染色体结构，这里给出具体实例：图6所示为一个包含7个建库候选点（即m=7）的配送网络图，根据编码规则，随机生成的一个染色体如图7所示。

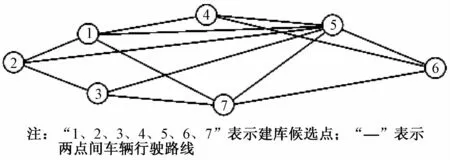
图6 配送网络图（m=7）

图7 多目标演化算法染色体编码示意图

图7子段1显示，5号候选点为建库选址点，其他各点被定义为物资需求点。子段2表示车辆从建库选址点5到各需求点间行驶所需经过的路段数，例如子段2首位表示从选址点5到需求点2所需经过的路段数为2。并由图6可知，符合该路段数的行车路线方案有两条，分别为5→1→2和5→3→2，进而算法会在众多符合的方案中随机生成一种，通过代入模型进行解码，得到各染色体的多目标函数值集合。同理，可以得到建库选址点5到其余各需求点的行车路线方案，如表1所示。

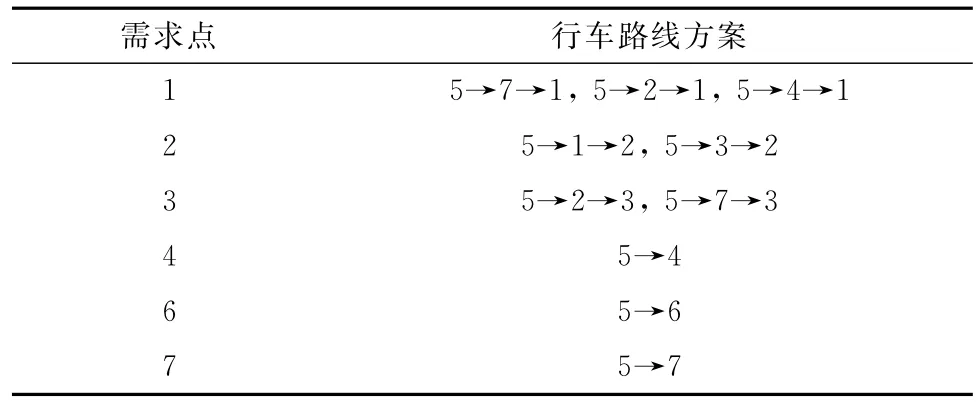
表1 建库选址点5到各需求点的行车路线安排

2.2 Pareto非劣解集合

在单目标优化问题中，可以通过比较适应度值的大小寻找问题满意解；而在多目标优化问题中，各目标之间由于权重、量纲不同，目标解之间存在无法比较和冲突的现象。这种无法简单进行相互比较的解，称为Pareto最优解或非劣解。求解非劣解集的算法有直观比较法、带簿记的直观方法以及KIP方法等[24]，这些传统算法都面临着运算时间长、收敛速度慢等问题。因此，本文基于模型解码后的可行解集合，采用快速非劣排序法[19]来求非劣解集合。尤其是在目标函数较少时，该算法明显优于其他算法，并且该算法得到的解集均匀地分布在Pareto最优前沿面上，最终可得排序的Pareto优化前沿。

2.3 遗传算子的设计

在用遗传算法求解多目标优化问题时，一般通过选择操作识别出好的染色体，而交叉、变异操作与求解单目标问题时一样。本文针对性地提出了多目标遗传算法的选择、交叉和变异策略，具体策略如下：

（1）选择操作。遗传算法的选择操作使用精英保留策略和锦标赛策略两种方法。假设该算法初始种群有popsize个个体，精英保留策略是指选择第一Pareto前沿面上（F1）的若干个个体p，使其不执行交叉、变异等操作，直接保留到下一代，从而加快算法的快速收敛；而其余个体（popsize-p）则通过锦标赛策略被选出。其主要思想是：①从种群中随机选择两个个体，记为P1和P2；②比较P1和P2，选择其中处于占优的Pareto优化前沿｛F1，F2，…｝的个体；如果P1和P2处于同一个Pareto优化前沿，则选择拥挤程度小的个体。选择操作如图8所示。

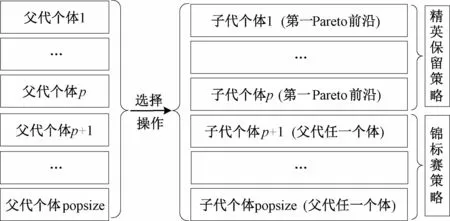
图8 遗传算法选择操作示意图

（2）交叉操作。交叉操作是确保种群多样性的主要手段，本文采用多点映射交叉策略。由于本算法染色体编码结构特殊，每条染色体所含选址方案信息不同，故不能随机对两两染色体进行交叉、变异。因此，首先需要对染色体按首位（建库点）序号进行排序，然后对包含相同选址方案信息的染色体进行多点映射交叉操作。多点映射交叉的思想是：①对排序后的染色体进行两两组队，不能组队的染色体直接保留下一代，不参与交叉操作；②利用子段1的映射关系，对组队的父代染色体的子段2进行多点交叉。这里仍然以该配送网络图包含7个建库候选点（即m=7）为例对该策略进行阐述，如图9所示。父代种群共有6个染色体，分别描述了在点3、5、7建库的6种行车路线方案，如图9（a）所示；然后对父代种群按各染色体首位（建库点）序号进行排序，如图9（b）所示，假设交叉点为子段2的第2位，交叉位数为2位（图9（c）中用*表示）。为便于研究，这里只对第1组染色体的变换过程进行展示。根据映射交叉的思想，对于染色体1而言，首先在其子段1中找到子段2上要交叉的路段数所对应的需求点信息，分别为需求点6和需求点1（图9（c）中用箭头①表示），进而在染色体2中找到表示车辆从供应点7到需求点6和1之间行驶所需经过路段数的值（图9（c）中用箭头②、③表示），将其与染色体1中对应的交叉位上的值进行置换（图9（d）中用箭头④、⑤表示），即可得到染色体1经过多点映射交叉后的染色体1*，同理可得该组染色体2和其余染色体多点映射交叉后的新种群，如图9（d）所示。

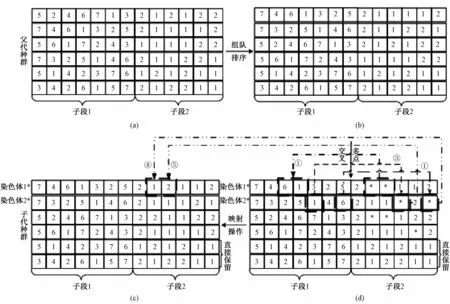
图9 遗传算法交叉操作示意图

（3）变异操作。变异操作是确保种群多样性的辅助手段，本文采用多点变异策略，即对一个染色体中子段2内的多个基因位上的值进行变异。由于各染色体采用实数编码方式，并且，子段2中各基因位所含信息不同，故不能随机对各基因位进行两点变异或倒序变异，而是采用再次生成该基因位上的值来达到变异的效果。这里仍然以该配送网络图包含7个建库候选点（即m=7）为例对该策略进行阐述，如图10所示。父代种群共有两条染色体A、B，分别描述了在点5、7建库的行车路线方案，如图10（a）所示，假设变异点分别为子段2的第2、3位，变异位数为2位。再次以路段数集合为数据池，按照泊松分布的概率对该变异位上的值进行重新生成，则多点变异后的种群如图10（b）所示。由图10（b）可见，染色体A子段2中第2、3位变异后的值分别为1和1，与变异前相比，路段数取值有所改善。

图10 遗传算法变异操作示意图

2.4 算法的操作流程

（1）设置遗传算法的相关参数。种群大小popsize，最大迭代次数maxgen，泊松分布函数系数λ，交叉概率pc和交叉位数crossover_length，变异概率pm和变异位数mutation_length。

（2）种群初始化。随机生成一个染色体，判断是否满足所有约束条件，若满足，则将个体放入种群中，否则舍弃；继续生成新染色体，直至种群中的染色体个数达到种群大小，记为oldchrom。

（3）计算种群中每个染色体的各目标函数值和Pareto非劣解集合。

（4）进行选择操作。首先采用精英保留策略选择第一Pareto前沿面上（F1）的若干个个体subchrom1，使其不执行交叉、变异等操作，直接保留到下一代；然后采用锦标赛策略选出popsize-subchrom1个染色体，生成新的种群subchrom2。

（5）交叉操作。对subchrom2的每个染色体以交叉概率pc和交叉位数crossover_length进行多点映射交叉，产生新种群subchrom3。

（6）变异操作。对subchrom3的每个染色体以变异概率pm和变异位数mutation_length进行多点变异，产生新种群subchrom4。

（7）将subchrom1和subchrom4合并为一个新种群chrom，将新种群chrom记为oldchrom。

（8）判断是否达到收敛条件，即解集是否均匀分布在Pareto最优前沿面上，若满足，则输出Pareto最优解集和相应的选址-路径方案并退出计算；否则，返回（3）。

3 数据与结果

在图1中鄂南油田危险品仓库候选点共有18个，需要从中选择一个建立县级油田危险品物资仓库，为鄂南4个油田共584口开油井的生产提供化学药剂等物资，如表2所示1）以下数据均来源于中国石油化工股份有限公司华北分公司，截至于2015年12月。

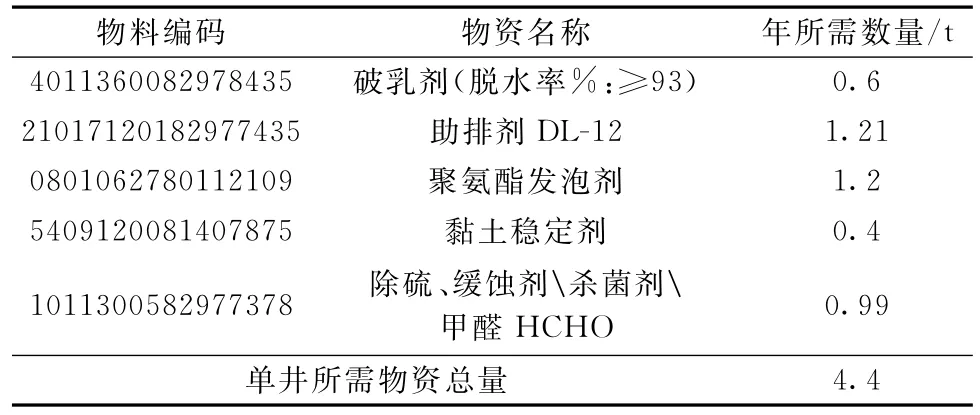
表2 油井生产年平均所需(危险品)年物资量(折算至单井)

各候选点的建站及初始启动费用已知，如表3所示，公司计划从18个候选点中选择一个作为危险品物资仓库的建库选址点。同时，各县城还要作为危险品物资运输的中途停靠节点，负责对危险品运输车辆进行必要的安全检测和给养补充。

表3 候选点的建站及初始启动费用

特别指出，鄂南油区当前共有3种可运输危险品物资的特种车型，每种车型的装载量分别为5 t、10 t和15 t。依据本文提出的鄂南油区危险品双层配送网络，首先通过大运载车辆（15 t）由危险品物资仓库以最为便捷的通道运往各中途停靠节点；进而，通过相应车型对需求进行分割，再由中途停靠点运往所辖区域内的油井。而本例主要研究上层网络的仓库选址及车辆路径问题，并将中途停靠节点抽象为虚拟物资需求点，汇集了该点所辖区域各井口的物资需求。

关于路段危险度等级的确定，已有的研究成果主要通过路面平整度、路网安全防护程度和区域人员密度等因素来判断各路段的危险度等级[25-26]。基于这些因素并参考国家道路划分标准，本文假设适合于该问题的危险度等级划分标准为高速、高速&国道、国道、国道&省道、省道以及省道&县道6个等级，并分别赋予相应的危险度值1、2、3、4、5、6，其中，危险度值越大，该路段危险度等级越高。

3.1 算例描述

根据上述分析，首先对各需求点的下辖油区范围进行划分，考虑到鄂南油区复杂的地理环境状况，这里以交通通达度为主，以就近原则为辅作为划分标准，将鄂南油区各油井的物资需求分解为18个区，各区所辖油井数及年所需物资量已知，如表4所示。

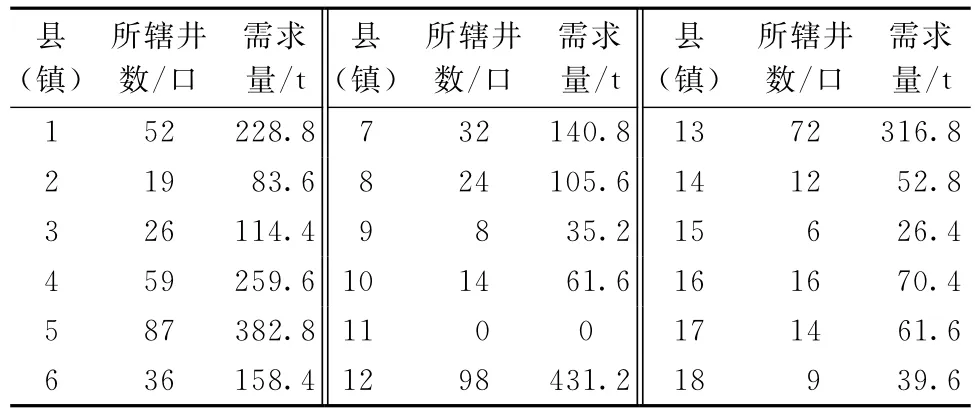
表4 各区所辖油井数及年物资需求量

该仓库选址及车辆路径问题可描述为：存在一个18个节点、44条边的网络图，如图11所示，路网中各路段的实际驾车距离、驾车最短时间以及路段危险度等级均在图中表示。图11中，点1～18为危险品仓库候选点建址所在地，由图11可以看出，在选址和运输过程中受到危险品潜在危害的居民点2）各居民点所在位置用鄂南地区各乡（镇）政府所在地表示有106个，居民点中只有序号前25位的居民点在备选点的危害辐射半径内，受到危险品仓库潜在危害的威胁，具体数据如表5所示。其余各居民点仅受到运输风险的威胁，所需各居民点的人口数量和区域面积已知，具体如表6所示。其余各参数值为：β1=3 km，β2=1 km，τ=2，Qz=15 t，θ=4万 元，cij=0.851 9元/（t·km-1）。

3.2 结果分析

3.2.1 Pareto最优解集 基于上述数据，本文使用Matlab8.5编制程序，通过多目标演化算法去求解MOLRPOHMT模型，并设置了遗传算法的相关参数。如种群大小为200个，最大迭代次数1 000代，泊松分布函数系数为1.2，交叉操作中pc=0.7、交叉位数为2位，变异操作中pm=0.025、变异位数为6位。程序运行5次，得到了由22个非劣解拟合的全局Pareto最优前沿面和局部Pareto最优解（可行域），如图12所示。将这22个解解码后，选取其中占比率最高的3种选址方案和与之对应的6种行车路线安排，如表7所示。

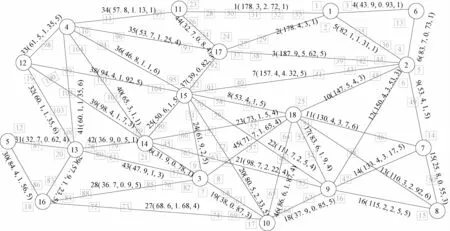
图11 鄂南油区选址-路径路网图

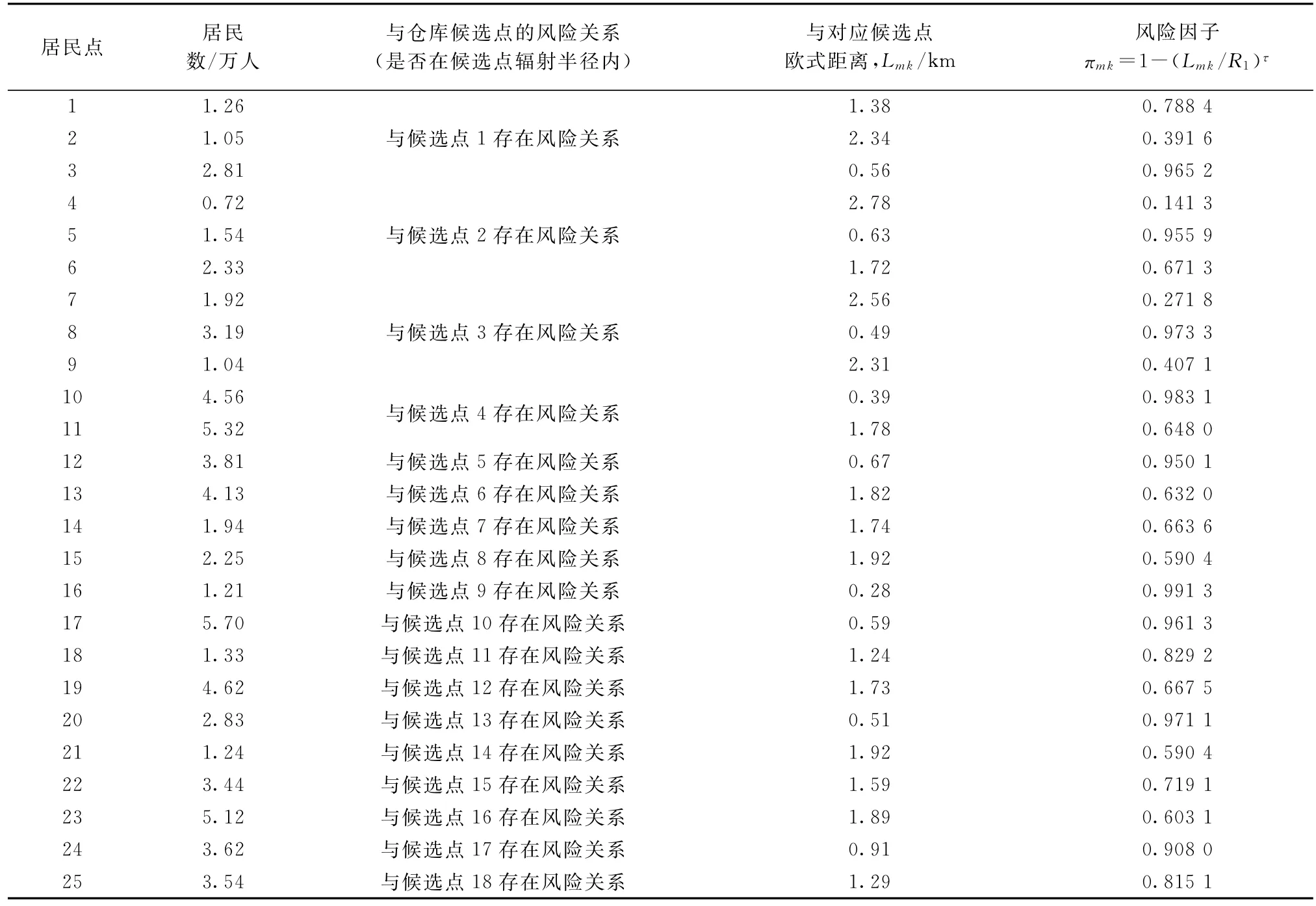
表5 选址风险威胁的各居民点人口数及风险因子

由图12可以看出，22个非劣解主要分布于空间中A、B、C等3个区域，而其余178个局部最优解却以这3个区域为聚类中心，均匀分布于由22个非劣解拟合而成的全局Pareto最优前沿面上。需要指出的是，该聚类分布与表8的计算结果一致，3个聚类中心描述了3种仓库选址方案，选址方案A选择候选点11作为建库所在地，该建库点总成本最小，但产生的风险较高、可靠性不强；选址方案B选择候选点13作为建库所在地，该建库点产生的风险较低、可靠性较强，但总成本较高；选址方案C选择候选点14作为建库所在地，该建库点在成本控制、风险量化和运输可靠性方面，相对于其他两个建库点较为折衷。另外，在每个仓库选址方案下又包含两种行车路线可供决策者选择。最终，决策者可以基于这6种选址-路径方案，并通过决策评价系统做出最优方案的选择。

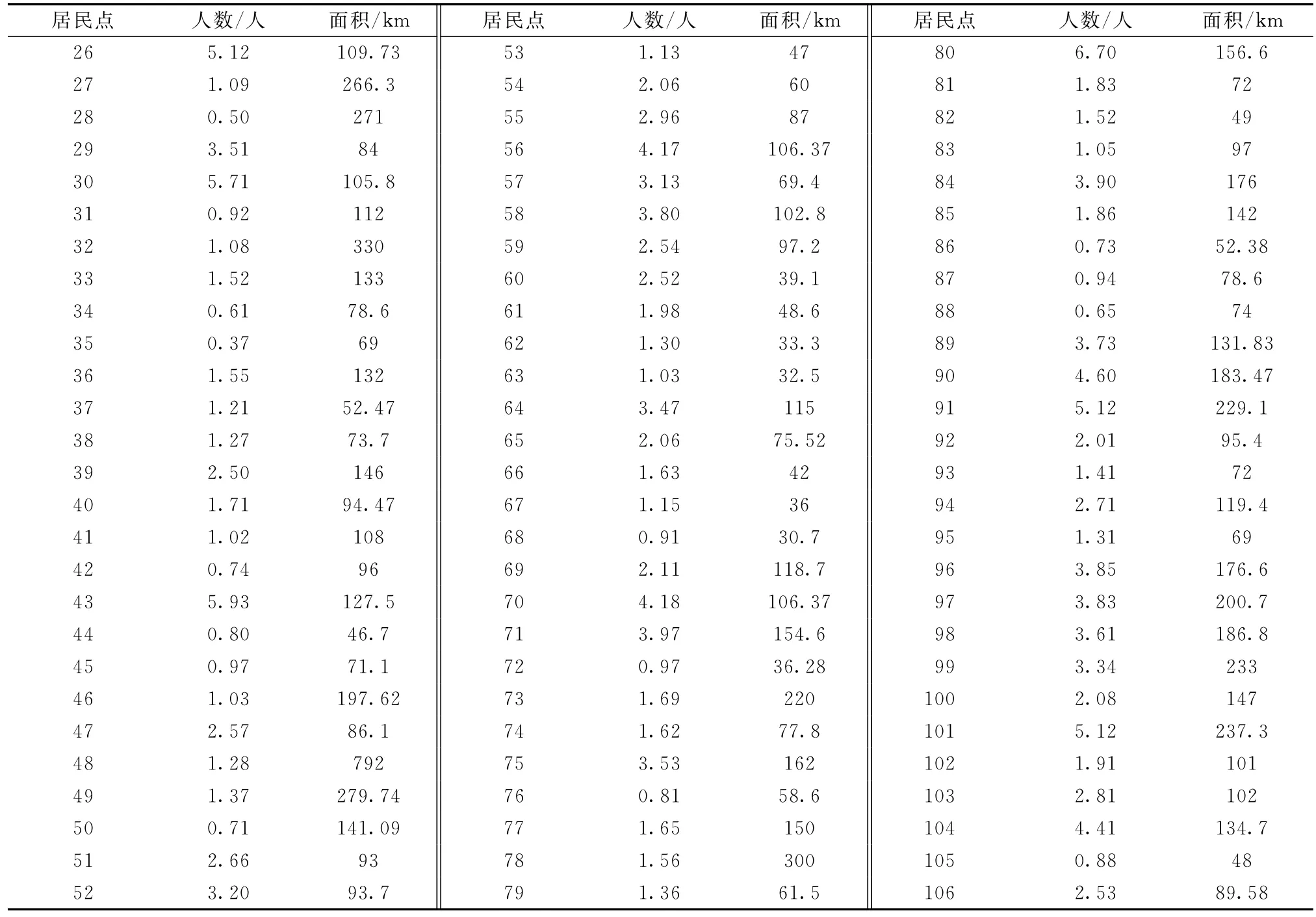
表6 运输风险威胁的各居民点的人口数及区域面积

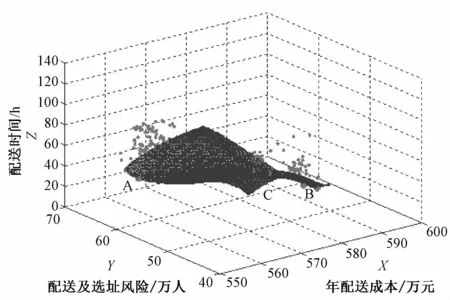
图12 Pareto最优前沿面

3.2.2 算法性能分析 与单目标不同，多目标优化性能的度量主要有3个标准：①算法不再产生新的改善解；②Pareto最优解集收敛并均匀分布在Pareto最优前沿面上；③保持解空间（可行域）的多样性。基于此，本文引入平均进化率、非劣解分布离散度和解空间分布多样性等指标来衡量算法的性能。

（1）平均进化率。平均进化率用来衡量算法产生新的改善解的可能性，其定义为[27]

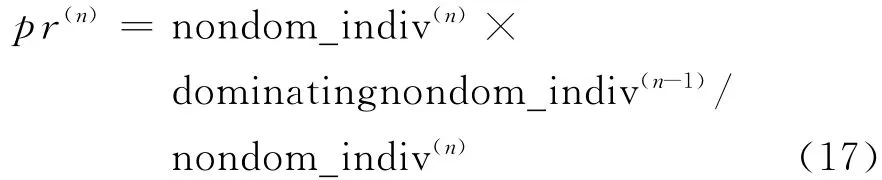
式中：pr（n）为第n代的进化率；分子表示被第n代所占优的第n-1代的非劣解个数；分母表示第n代的非劣解个数。根据式（17），计算出平均进化率，如图13所示。由图13可见，随着进化代数的增加，进化率减小，算法收敛，找到新的改善的非劣解的几率也就越来越小。

（2）非劣解分布离散度。非劣解分布离散度用来描述Pareto最优解集（非劣解）是否收敛并均匀分布在Pareto最优前沿面上，其定义为[19]

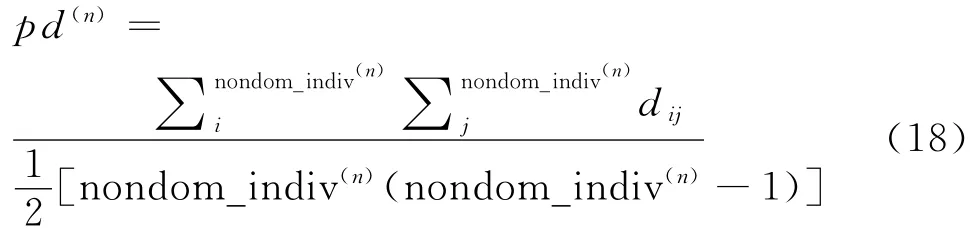
式中：p d（n）为第n代的非劣解分布离散度；分子表示第n代中各非劣解之间的欧式距离之和；分母表示各非劣解之间匹配的个数。根据式（18），计算出非劣解分布离散度，如图14所示。由图14可见，随着进化代数的增加，离散度降低，各非劣解之间的平均欧式距离不再发生变化，Pareto最优解逐渐收敛并均匀分布在Pareto最优前沿面上。

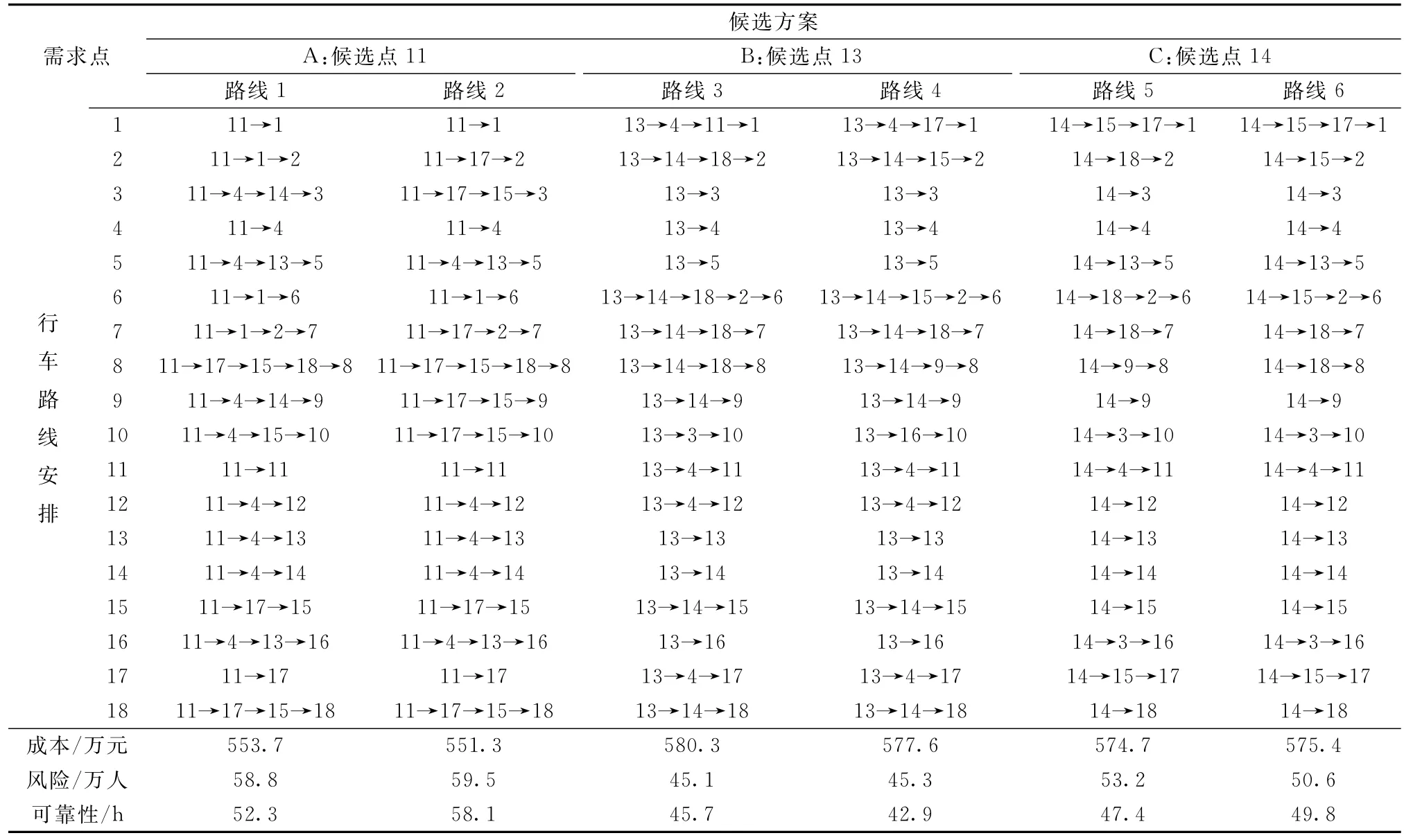
表7 Pareto最优解所对应的选址-路径方案

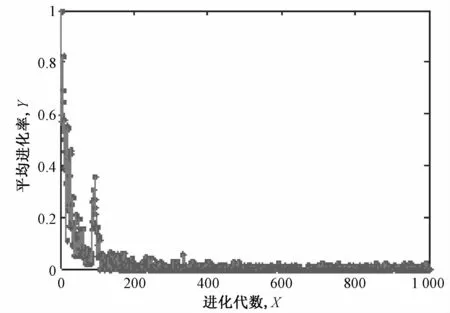
图13 平均进化率

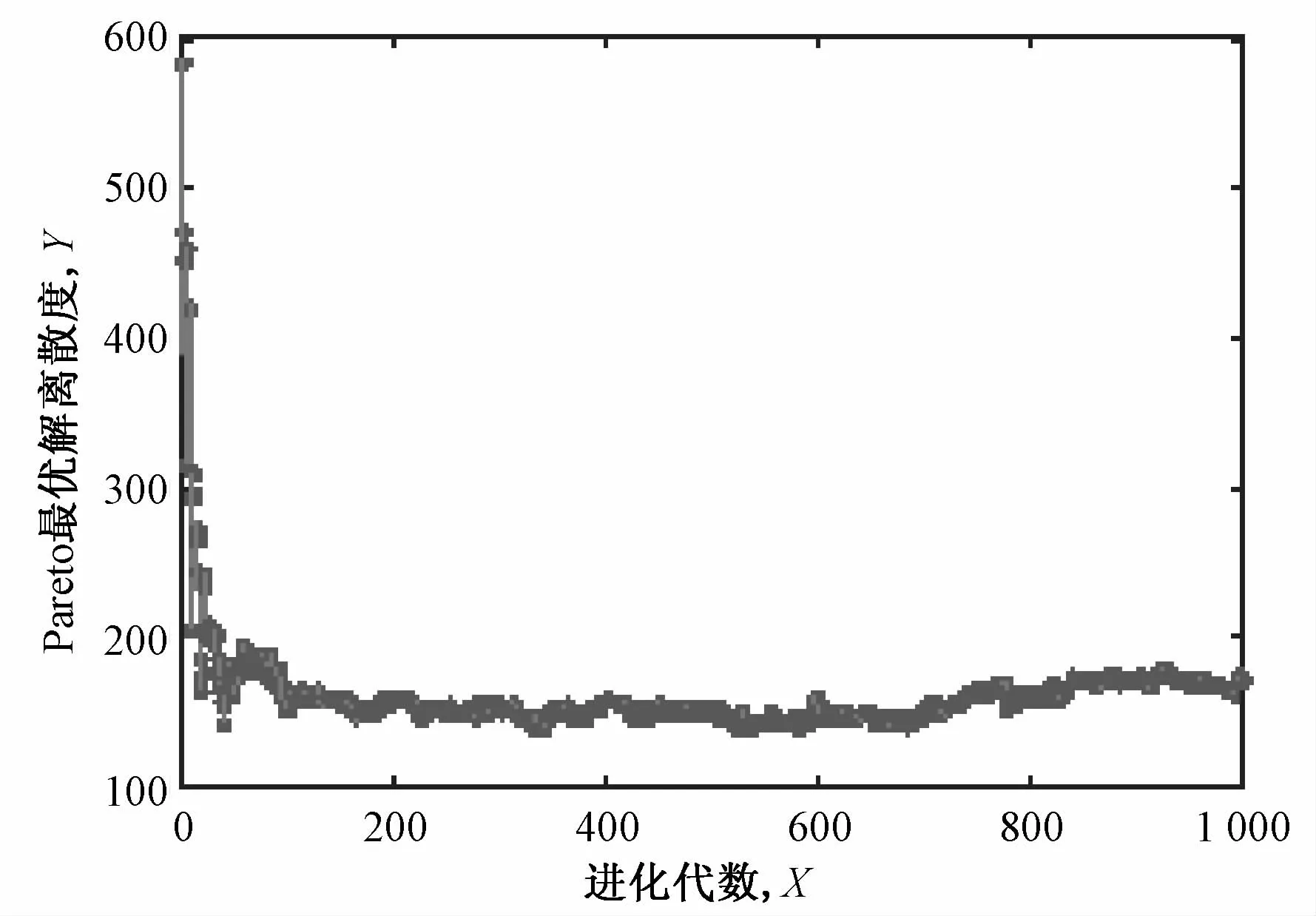
图14 非劣解分布离散度

（3）解空间分布多样性。该指标用来衡量多目标演化算法交叉、变异效果，进而反映解空间分布的多样性，对其度量值定义为

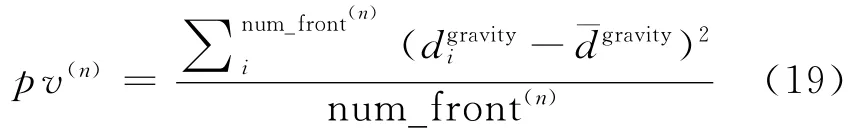
式中：p v（n）为第n代的解空间多样性度量值；分子表示第n代中各Pareto前沿面之间的欧氏距离（用各前沿面间的重心距离表示）及其均值之间的偏离程度；分母表示第n代Pareto前沿面的个数。图15所示为根据式（19）绘出的解空间多样性度量值变化图，由图15可见，度量值高低值连续变化较为一致。

图15 解空间分布多样性

为了更加清晰地描述解空间分布的多样性，基于上述数据绘制了相应的箱线图，如图16所示，除个别异常值外，度量值主要分布于[0，150]，解空间分布较为合理，多样性较好。特别指出，该指标在平均进化率和非劣解分布离散度收敛性较好的前提下，验证了算法参数设置的合理性和生成的非劣解集的有效性。

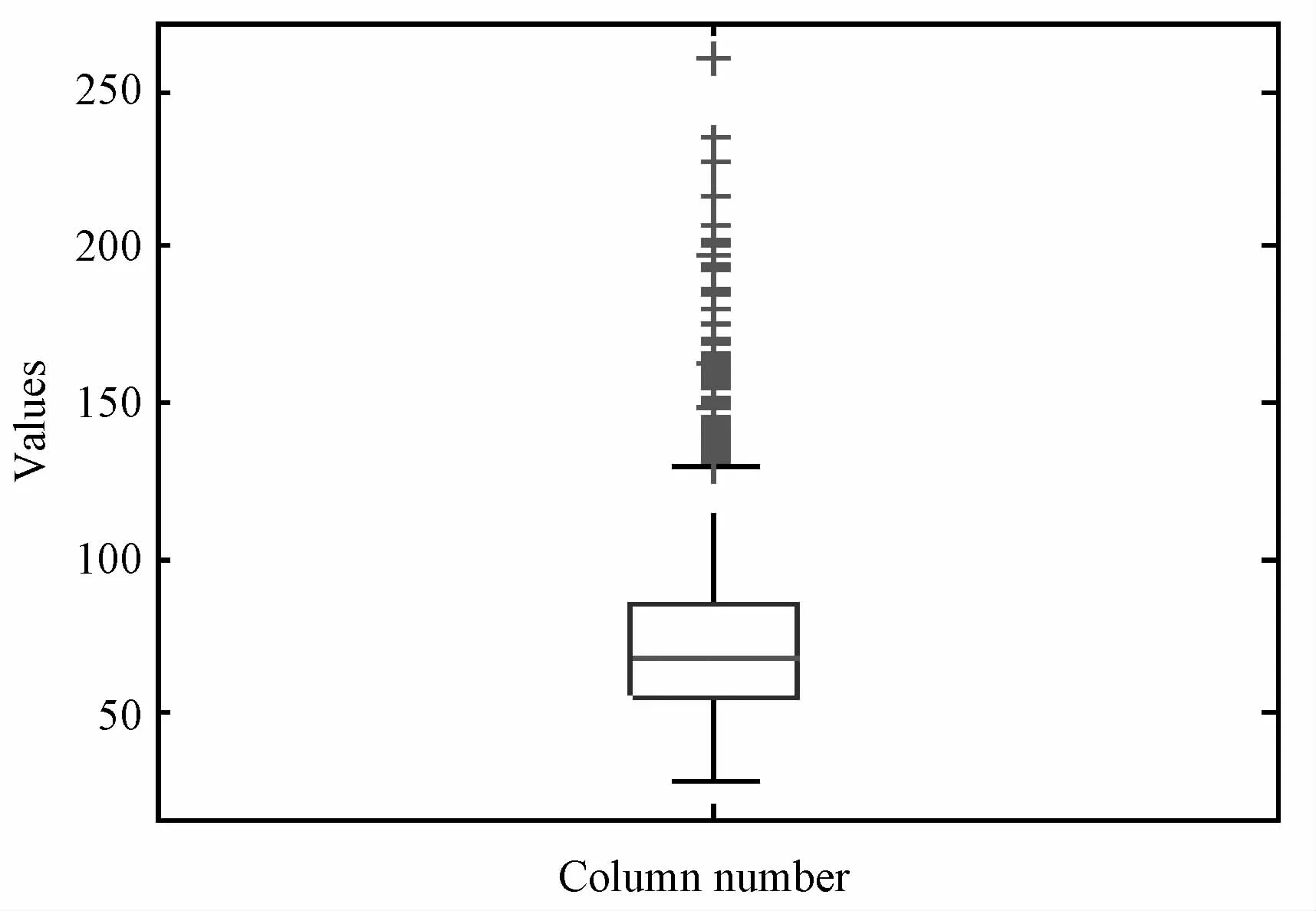
图16 解空间分布的箱线图

3.2.3 最优方案的选择 由于这6种选址-路径方案为Pareto最优方案，其核心思想就是不考虑目标权重和决策者偏好，使得方案之间没有明显的优劣之分，均为可供决策者选择的满意方案。但考虑到本文的应用背景，有必要通过多目标评价模型对方案集进行再次筛选，找到最优的选址-路径方案。因此，本文基于成本、风险和可靠性3个目标，引入随机多属性可接受度分析方法对这6种选址-路径方案做出评价；基于表7提供的6种选址-路径方案各目标的原始数据，通过采用改型SMAA-2方法提供的4种分析工具对候选方案集进行分析以选出最优方案[28]，原始数据及JSMAA[29]软件计算结果如表8所示。

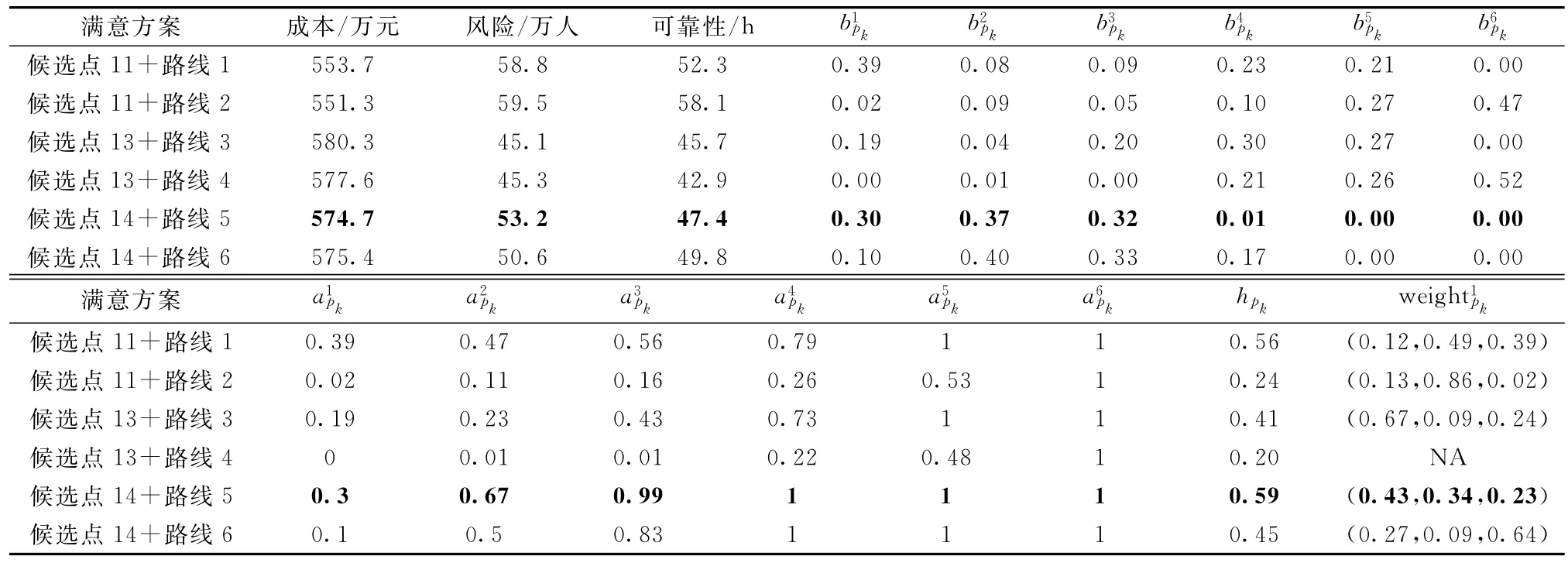
表8 SMAA-2计算结果

由表8可知，“候选点14+路线5”这一选址-路径方案获得最高的可接受度系数，为0.59。该数据表明，假定决策者对各目标权重没有任何先验信息和特殊偏好，“候选点14+路线5”方案有59%的概率被选作最优方案。因此，该方案应作为油田危险品仓库选址和配送路径选择的最优方案。对应于“候选点14+路线5”这一最优方案的中心权向量为（0.43，0.34，0.23），该数据表明，选择该方案为最优方案的决策者认为各目标的隐藏偏好权重系数分别为0.43、0.34和0.23。

4 结语

危险品事故往往会产生灾难性的后果，研究油田危险品物流系统的管理方法和模型具有十分重要的意义。本文从选址-路径问题集成化的角度研究鄂南油田危险品物流系统。首先提出了适合于鄂南油田的危险品运输的双层配送网络，并以道路危险度等级为约束，构建了一个总成本最小、风险最低、可靠性最强的油田危险品物资运输的多目标LRP模型；进而，通过多目标演化算法得到了Pareto最优解集合，并采用随机多属性可接受度分析方法对Pareto最优解集进行再次筛选，求得最优选址方案和最优配送路线。求解结果显示，“候选点14+路线5”为最优选址-路径方案，并且选择该方案为最优方案的决策者认为各目标的隐藏偏好权重系数分别为0.43、0.34和0.23。最后，以平均进化率、非劣解分布离散度和解空间分布多样性等指标衡量了算法的性能。性能显示，解空间分布多样、平均进化率和非劣解分布离散度等指标收敛性较好，验证了算法参数设置的合理性和生成的非劣解集的有效性。本文的模型和算法对于进一步补充和完善危险品物流系统的选址-路径问题具有一定的理论意义，对油田、煤矿等行业的物流系统优化具有重要的现实意义。本文的不足之处在于，模型中没有考虑多库选址、不确定性风险的动态变化等特征，这是今后研究的主要工作。