基于信任度数据融合的频谱感知算法
2018-08-17李雄雄孙继康
李雄雄,吴 键,孙继康
(南京理工大学机械工程学院,江苏 南京 210094)
0 引言
随着信息技术的发展,在认知无线电领域中,频谱感知技术正成为研究热点。现有的频谱感知技术一般遵循奈奎斯特采样定理,即采样率是采样信号最大频率值的2倍。在实际应用中,为了获得更宽的频谱感知范围,必须采用高采样率的模数转换器(analog-to-digital converter,ADC)。这样往往会大大增加硬件成本,对嵌入式微处理器的存储容量和计算速度也提出了更高的要求。因此,宽带信号频谱感知的研究将主要集中在如何通过较低的采样率进行频谱感知。
在低于奈奎斯特采样率[1]的情况下进行频谱感知,主要有基于时延和多速率两种频率估计算法。本文在深入研究这两种算法的基础上,提出了一种基于信任度数据融合的频谱感知算法,能有效对基于时延和多速率的两种算法所存在的问题进行优化与改进。由于低采样率会造成频谱混叠现象,基于信任度数据融合的频谱感知算法采用多组不同采样速率的ADC进行采样,能大大降低频谱混叠发生的概率。在频率估计方面,本文综合了基于时延和多速率两种频率估计算法,并对多路径计算出的频率值进行了基于信任度的数据融合,能大大降低频率值的误判率、提高检测率,从而获得更好的频谱感知范围。
1 低采样率的频谱感知模型
在低于奈奎斯特采样率的情况下,直接对宽带信号进行低速采样会造成频谱混叠,即信号经过快速傅里叶变换(fast Fourier transform,FFT)后,在频谱某一个频段的分布上,高频信号和低频信号分量会相互重叠。频谱混叠如图1所示。

图1 频谱混叠示意图
时域信号经过快速傅里叶变换后(以奈奎斯特采样率进行采样),频谱分布图如图1的上半部分所示;在低于奈奎斯特采样率的情况下则会频谱混叠,经过快速傅里叶变换后的频谱分布如图1下半部分所示。
本文研究的重点主要集中在如何以较低的采样率,利用频谱信号稀疏的特性[2],进行信号的频谱感知,并获得信号的频谱信息。频谱感知模型[3-4]如图2所示。

图2 频谱感知模型
对于低速采样得到的时域信号,在经过快速傅里叶变换[5]后,频谱的分布会发生混叠。如果信号稀疏度较低,只有一个非零值信号映射到频率单元中,则频率之间没有发生冲突。因此,本研究需要对频率进行估计,计算出真实的频率值。
频率估计主要有两种算法[6]。这两种算法都是以低于奈奎斯特采样率进行采样的。第一种是基于信号时延的频率估计算法。对于同一模数转换模块,该算法在不同时刻以相同的采样率对信号进行低速采样,得到相同速率下的信号。由于两组信号之间间隔一定的时间,该算法利用信号时域延迟,会引起频域相位旋转。第二种是基于多速率的频率估计算法[7]。该算法对于不同模数转换模块,其采样率也自然不同。在同一时刻,该算法分别以不同的采样率对信号进行低速采样,得到不同速率下的信号;然后采用模糊算法实现频率概率信息的估计,求得频率估计的唯一解。
2 两种频率估计算法
2.1 基于时延的频率估计算法
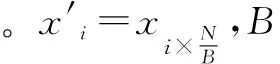
(1)

(2)
为了计算频率[8],可以通过将时域信号的延时转化为频域的相位旋转,利用相位差来计算非零频率的位置f,同时估算出原频谱中的非零频率的频率值Xf。
2.2 基于多速率的频率估计算法
在频谱感知模型中,一个A/D以Fs1采样速率的低速采样后得到x1,另一个A/D以Fs2采样速率的低速采样后得到x2。f1k、f2k分别为x1、x2经过快速傅里叶变换的频率值。
然而在低速采样中,经过计算后的频率并非真实频率值。其与实际频率之间可能相差了采样频率的整数倍。由于两个通道是独立的,求解出的模糊频率估计值也是独立的,因此可以采用合适的模糊算法来估算信号的真实频率值。根据文献资料,在不考虑噪声的情况下,真实频率值fk为:
fk=f1k+pkFs1=f2k+qkFs2
(3)
式中:pk和qk为模糊数。设A是实数集R上的模糊集,即A∈F(R)。如存在X∈R,有A(x)=1,且对任意λ∈(0,1]。当Aλ是闭区间, 则称A是一个模糊数。若模糊数A的支集suppA有界,则A被称为有界模糊数。
根据式(3)可以看出,在确定模糊数的值以后,就可以计算出频率真实值。在考虑噪声扰动的情况下,一般可以通过取式(4)的最小化绝对值(即最小噪声值)来确定pk和qk。
(pk,qk)=argmin|f1k-f2k+pkFs1Fs2|
(4)
模糊数pk和qk的范围,可以根据估算频率真实值得到确定范围。
3 基于数据融合的频谱感知算法
如果一段需要感知的频段的频率分布稀疏度比较低[9],甚至在某一个窄带频谱范围内只有一个频率值,采用上述基于时延和多速率算法中的任意一种,都可以实现频率估计。但是,若一个频段内频谱分布稀疏度比较高,经过A/D采样后甚至发生频率冲突,即混叠过程中有两个及以上的非零频率值映射到同一个频率单元,则无法采用传统的频率估计算法实现频谱感知。基于信任度数据融合的频谱感知算法流程如图3所示。

图3 频谱感知算法流程图
针对上述问题,本文提出了一种基于信任度的数据融合方法[10]。该方法首先定义了一个模糊型指数信任度函数,对多条路径计算的数据间的信任度进行量化处理;然后,通过信任度矩阵度量各个路径计算所得数据的综合信任程度,以合理的方式分配各个数据在融合过程中所占权重;最后,可得到数据融合估计的最终表达式,以实现多路径数据的融合。
对两组不同采样速率的模数模块使用基于时延的频率估计算法,并各自提取其中一个转换模块,通过基于多速率的频率估计算法进行有效融合估计,能计算频率值个数、频率冲突点并估算频率值。在该改进的频率估计算法中,综合了两种频率估计算实现对某一频段的感知。
设三条路径计算后的数据分别为x1、x2和x3。如果x1(x2、x3)的真实性越高,那么x1(x2、x3)被其他数据信任的程度就越高。多路径计算数据间的这种信任程度被称为信任度。
为了对多路径计算后数据间的信任度进行统一量化处理,定义一个信任度函数bij,表示xi被xj信任的程度。
bij=f(xi-xj)
(5)
式中:i,j=1,2,3;0≤f≤1。
令:
(6)
式中:mij>0。
如果bij=0,表示第i个数据与第j个数据之间相互不信任;反之,则相互信任。如果一个路径的数据不被另外两个路径数据信任,则该数据在融合过程中将被删除。该处理结果受主观因素影响较大,不利于对频率值作出评判。
本文改进后的基于信任度数据融合的方法是将bij设为指数函数:
(7)
当图3计算出的两个频率值的差值大于上限值M时,那么二者不再相互信任,即bij=0。本文将bij定义为满足模糊性的指数函数形式,既避免了由于数据之间相互信任过程中的绝对化,又利用了模糊理论中隶属度函数范围确定的优点。在实际问题处理中,本方法具有高度的可实施性,能使处理后的数据更加准确和稳定。本文中,通过三条路径计算出的频率值,并根据数据间的信任度函数bij,建立信任度矩阵B:
(8)

在具体的数据融合过程中,用wi表示第i个路径计算的频率值xi在融合过程中所占的权重。由于wi的大小反映了从另外两条路径计算的频率值对第i个路径计算的频率值xi的综合信任程度,可以利用wi对xi进行加权求和,得到数据融合的表达式为:
(9)
在信任矩阵B中,信任函数bij仅表示计算得到的频率值xj对xi的信任程度,并不能反映其他路径计算的数据对xi的信任程度;而xi(i=1,2,3)的真实信任程度应该由bi1、bi2和bi3来综合体现。wi应该综合一个关于xi的各个子系统bi1、bi2和bi3的全部信息,所以需要求出一组非负数a1、a2和a3,使得:
wi=a1bi1+a2bi2+a3b3ii=1,2,3
(10)
其可以改写为:
W=BA
(11)
式中:W=[W1,W2,W3]T、A=[a1,a2,a3]T。
因为bij>0,所以信任度矩阵是一个非负矩阵,并且该对称矩阵存在最大模特征值λ>0,使得λA=BA。求出λ及对应特征向量A,满足ai>0,则W=λA,可以作为对各个路径计算数据间综合信任程度的度量,即:
(12)
对wi进行归一化处理,得:
(13)
对所有路径计算得到频率值融合估计的最终结果为:
(14)
比对每次计算出的结果与上一次的计算结果[11]。如果差值小于设定的误差值ζ或者已经达到设定的迭代次数n,则结束计算,将最后的频率计算结果视为最终结果。
4 仿真分析
设置两组采样速率分别为50 MHz和65 MHz,采样点N=1 024。根据前文介绍的改进算法流程,本节对改进后的频率估计算法进行了仿真,并与传统的基于时延的频率估计算法和基于多速率的频率估计算法进行了对比,详细分析了3种算法中信噪比(signal noise ratio,SNR)对检测概率的影响、频谱稀疏度对误判率的影响。然后,分析了在改进的算法中,不同迭代次数下信噪比对检测概率的影响,还给出了频谱感知的频率感知范围,并与原信号频谱作比较。
基于时延的频率估计算法、基于多速率的频率估计算法与改进后的频率估计算法中,信噪比对检测频率的影响如图4所示。其中,信号的稀疏度为10%,改进后算法的迭代次数为设置为5次。从图4中可以看出,随着信噪比的增加,三种算法的检测概率都越来越高,而改进后的频率估计算法明显优于其他两种传统算法,检测概率也更高。当信噪比足够低(达到-15 dB)或者足够高(达到10 dB),差异才不是特别明显。

图4 信噪比对检测频率的影响
3种算法中,信号稀疏对频率误判率的影响如图5所示。其中,信号的信噪比为0 dB,改进后算法的迭代次数设置为5次。
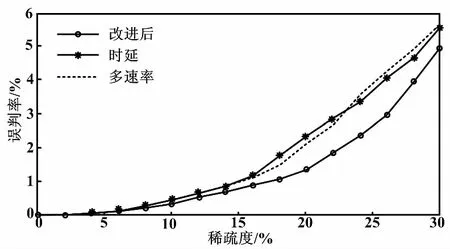
图5 稀疏度对误判率的影响
从图5可以看出,随着信号稀疏度的增加,即一个频段范围内包含的频率越来越多,会影响频率的检测与频谱感知,造成相应的误判率也越来越高。三种算法在信号稀疏度小于14%时,误判率相差不大,都能实现对频率的准确判断。但是当信号稀疏度大于14%后,改进后的算法误判率明显低于其他两种传统算法。
改进后的算法在不同迭代次数下信噪比对检测概率的影响如图6所示。信号的稀疏度为10%。
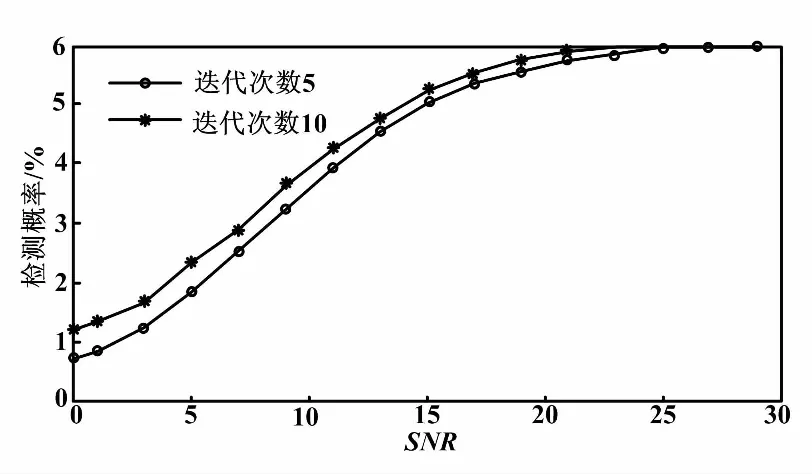
图6 不同迭代次数下信噪比对检测概率的影响
从图6中可以看出,随着迭代次数的增加,经过每次迭代计算,推算能力增加,系统算法检测错误的能力也逐步增强,检测概率也随着增加。例如当信噪比为-4 dB时,迭代10次的检测概率比迭代5次的检测概率高出约5%。并且,经过多次仿真验证说明,当迭代次数大于10次以后,该曲线基本达到稳定,不会随着迭代次数的增加检测概率而增加,基本收敛,达到最优。
对比原信号频谱图与重构信号频谱图波形:信号稀疏度为10%,采样信号的带宽为500 MHz,信噪比为0 dB,信号中混有110 MHz、220 MHz和310 MHz三个频率,原信号的频谱图以正常的奈奎斯特采样率进行采样。对比可知:重构的信号频谱图能较好地再现原信号的频谱分布;与原信号频谱图相比,频率值误差比较小,说明信号频率在相对稀疏的情况下,采用改进的频率估计算法能较好地进行频谱感知,重构信号频谱分布图。
5 结束语
为了更好地实现频谱感知,本文在两种传统频率估计算法的基础上,提出了一种改进后的频率估计算法。首先,介绍了传统频率估计算法存在的问题。随着信号稀疏度的增加,在一个窄带频率单元内发生频率冲突的可能性会越来越大。然后,针对存在的问题,在改进后的算法中,运用了一种基于信任度的数据融合方法,将基于时延的频率估计算法与基于多速率的频率估计算法这两种算法进行了有效数据融合,大大增加了频谱感知的信号稀疏度与检测概率,同时也降低了频率冲突发生率与误判率。最后,对改进后的频率估计算法的研究通过Matlab进行了仿真分析,验证了改进算法在检测概率、误判率等方面明显优于传统方法。
