轻烃分离装置液化气C5+含量软测量应用
2018-08-17金晓明
周 丽,冯 凯,金晓明
(1.浙江中控软件技术有限公司,浙江 杭州 310053;2.浙江大学智能系统与控制研究所,浙江 杭州 310027)
0 引言
混合轻烃气体的分离在石油化工行业十分常见。其原理是利用被分离组分的挥发度不同,实现轻重组分的分离。某些炼油加工装置,例如常减压、催化裂化或催化重整的后续装置常要进行C4-和C5+组分的分离。其中:C4-作为液化气的基础组分从塔顶部拔出,C5+作为汽油调和组分从塔底部拔出。对于塔顶组分液化气,C5+组分作为杂质,需要严格控制其含量。因此,获取塔顶油气的C5+含量已成为该塔质量控制的关键。
以多变量预测控制[1]为代表的先进控制技术和以实时优化为关键的过程优化技术能大大提高工业装置的经济效益。其中,以软测量技术[2]为核心的产品质量预估技术在先进控制中发挥着重要作用。本文在某工业装置上,采用偏最小二乘法(partial least squares,PLS)建模,实现了对液化气C5+含量的在线实时计算。
1 辅助变量筛选
在实际生产过程中,由于在线检测技术尚未成熟或者设备费用昂贵等原因,许多过程变量尚不能被实时监测,如精馏塔产品的组分含量、化学反应的转化率、反应器中反应物的浓度等。软测量技术因其容易实现和成本低廉,得到了越来越多的关注和应用。软测量技术是通过对一些容易测量的变量(称为辅助变量)构建数学模型,对生产过程中难以实时监测的变量(称为主导变量)进行估计,从而达到以软件代替硬件,得到难以测量的变量实时值的目的[3]。软测量技术主要包括数据采集与预处理、辅助变量选择、软测量模型和偏差校正等[2]部分。其中,最关键的是建立“最优”软测量模型方程。
软测量模型是软测量技术的核心。PLS方法的多变量回归模型由于方法简单、模型结果易解释,在工业的复杂环境下得到了广泛的推广和应用[4-6]。主流的先进控制系列软件,例如Aspen公司的Aspen IQ、HONEYWELL的Profit Sensor、中控的APC-Sensor都包括PLS方法的基础用法和功能。在模型结构确定的情况下,对原始数据的预处理和对辅助变量的选择,已成为软测量模型能否获得良好效果的关键。
辅助变量的选择直接影响着软测量模型的准确性和可靠性。选择合适的辅助变量,不仅可以精确地预测主导变量的变化,还可以简化运算,消除噪声[7]。好的辅助变量应该在包含尽可能多的过程信息的同时,利用尽可能少的变量。
辅助变量的选择可以从机理入手,也可以从分析历史数据入手[7]。机理分析需要熟悉装置工艺特性,通过对过程的机理、装置工艺、生产状态分析,找出与主导变量有明显关系的参数;然后,建立软测量模型,预测主导变量的变化[7]。历史数据分析只需从数据出发,选择对主导变量影响较大的变量,剔除对主导变量影响较小或者含有较多冗余信息的变量[7],再通过回归等方法建立软测量模型。本文先运用历史数据分析,挑选出在数据上表现良好的辅助变量,再进一步结合工艺分析,对变量进行筛选,最终运用PLS方法建立软测量模型。
常见的辅助变量选择方法有逐步剔除法、逐步引入法、逐步回归法、主成分分析法、贝叶斯变量选择法和各种智能算法[8]等。
在介绍具体方法前,先给出具体变量的定义。假设主导变量为y,使用变量x1,x2,…,xp对y建模。模型为:
y=a0+a1x1+a2x2+…+apxp
(1)
记x1,x2,…,xp的回归平方和为SSRp,则:
(2)
式中:n为样本个数。
同理,当使用变量x1,x2,…,xi-1,xi+1,…,xp对y建模时,其模型为:
y=b0+b1x1+b2x2+…+bi-1xi-1+
bi+1xi+1+…+bpxp
(3)
记x1,x2,…,xi-1,xi+1,…,xp的回归平方和SSRp-1为:
(4)
则变量xi的偏回归平方和Si为:
Si=SSRp-SSRp-1
(5)
对变量xi的偏回归平方和作F检验,以判断xi是否引入,需构建统计量:
(6)
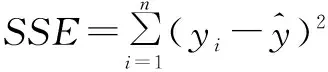
逐步剔除法的基本步骤是先用所有的自变量建立多元回归方程,然后选择偏回归平方和最小的变量并作F检验。若变量不显著,则将该变量剔除;否则终止剔除,直至所有不显著变量全部剔除为止。逐步剔除法的缺点是变量一旦被剔除,就再无机会进入回归方程。
逐步引入法的基本思想是先用每个辅助变量分别建立一元回归方程,然后选择偏回归平方和最大的变量引入回归方程。再与剩余变量分别建立二元回归方程,并选择偏回归平方和最大的变量进行F检验。如果显著则引入方程,如不显著则终止引入,如此循环直到没有变量可以引入为止。逐步引入法的缺点是一个变量一旦被引入,就再也无法剔除。
逐步回归流程如图1所示。
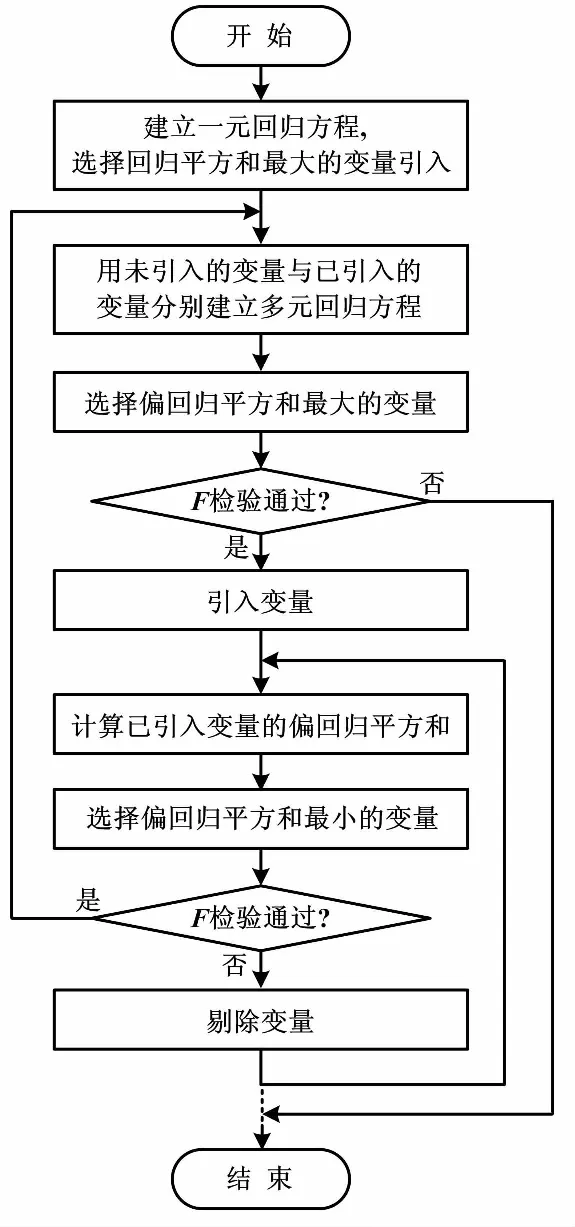
图1 逐步回归流程图
逐步回归法是一种“有进有出”的变量选择方法[9]。逐步回归的每一步,都要选择偏回归平方和最大的变量,在特定的显著性水平下进行F检验[10]。如果通过检验,则将该变量引入回归模型。同时,对已经引入的变量重新进行审视,以确定是否会因为新变量的引入而导致原有变量变得不重要。选择偏回归平方和最小的变量进行F检验,如果不显著,则剔除该变量。逐步回归的每一步,不仅需要判断是否引入或者删除一个变量,而且需要进行F检验,以确保每次引入新的变量后,方程只包含显著的变量。如此循环,直至没有变量可以引入和剔除。这里需要注意,引入变量F检验的显著性水平临界值为αin, 剔除变量F检验的显著性水平临界值为αout,则需取αin<αout,否则将导致死循环[11]。
逐步回归是应用非常广泛的一种变量选择方法。它通过不断“引入”和“剔除”变量,产生一系列的回归模型,最终建立一个局部“最优”的回归方程,使得所有进入回归方程的自变量在统计意义上都是显著的,所有未进入回归方程的自变量都是不显著的。
1.1 逐步回归方法筛选
在明确了软测量任务以后,选定待测变量,也就是主导变量,再通过进一步深入了解过程工艺和装置特性,初步确定用于软测量建模的辅助变量集合,称为软仪表建模的变量池。由于变量池内变量数目众多,且各个变量之间可能存在高度相关性,因此首先利用逐步回归的数据分析方法,挑选出能表征因变量变化的自变量。
在液化气C5+含量的软测量建模中,经初步工艺分析,共选取34个变量作为建模的变量池。这34个变量包括前续和后续装置的温度、压力和流量工艺参数。
在逐步回归建模中,引入变量的显著性水平为0.05,剔除变量的显著性水平为0.1,共选用173组数据。依次选入回归模型的辅助变量包括:稳定塔塔顶温度(X5),初馏塔塔顶温度(X3),稳定塔回流流量(X7)。逐步回归选入变量的步骤如表1所示,数据拟合效果如图2所示。

表1 逐步回归变量选择步骤表
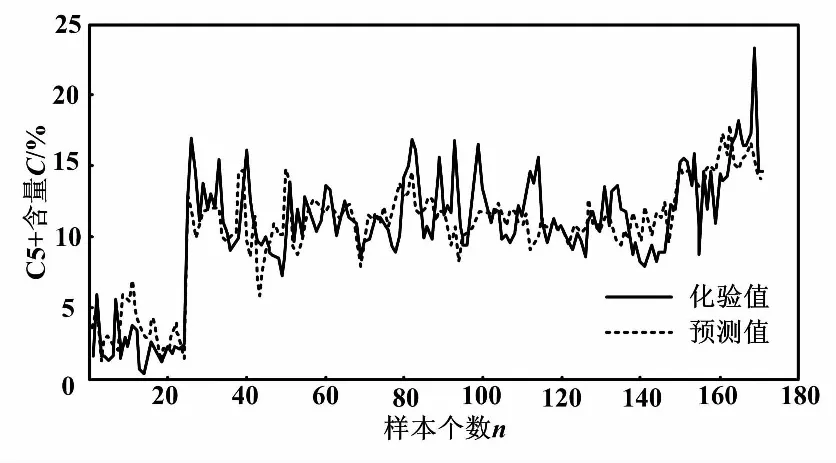
图2 逐步回归变量选择拟合效果图
从显著性水平可以看出,所有选中的变量都是显著的。逐步回归模型为Y=0.301 645×X3+0.593 352×X5-0.488 62×X7-68.981 6。
1.2 工艺分析方法筛选
逐步回归筛选变量的方法依托经过现场装置整理的数据,其本质是一种黑箱模型方法。由于采集的数据不可避免地在数据预处理过程中存在误差,例如一些时序匹配或者采样时间无法精确的问题,仅仅从历史数据分析角度选择辅助变量可能会因追求过高精度的建模效果而造成过度拟合,故需要对筛选的辅助变量进行工艺分析。
初馏塔是该装置的前续工段。初馏塔塔顶物料作为稳定塔的进料将长期影响液化气C5+含量。但是初馏塔塔顶温度和液化气C5+含量的采样检测点距离太远,经过对比另外几组分析数据,认为将初馏塔塔顶温度辅助变量更换为稳定塔第25层塔盘温度更为合理。
2 软测量建模
最终确定的软测量辅助变量为:稳定塔塔顶温度、稳定塔第25层塔盘温度、稳定塔回流流量。建模方法采用PLS回归。本文收集了100组建模样本数据,软测量模型离线预测效果如图3所示。
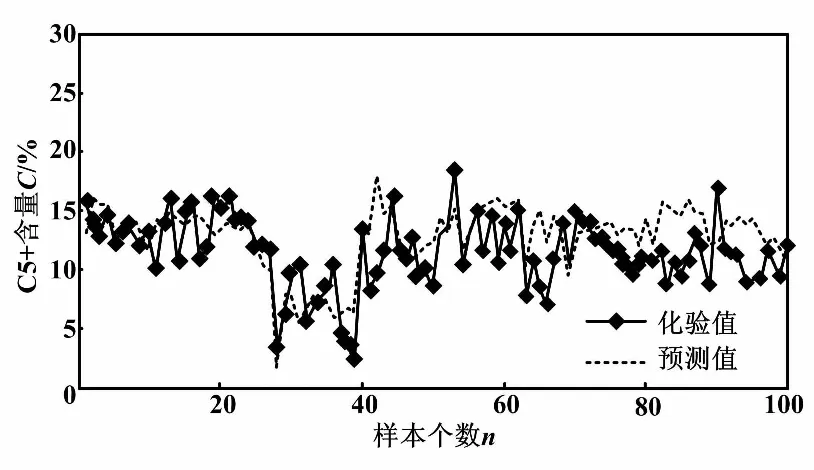
图3 软测量模型离线预测效果图
3 软测量模型在线预测效果
将软测量模型配置到分布式控制系统(distributed control system,DCS)上位机,利用OPC接口读取现场数据并且回写预测值。模型在线计算功能和校正功能通过软测量系列软件实现。模型运行约一个月后,采样间隔时间为1 h,样本数据约4 000组,软测量模型在线预测效果如图4所示。
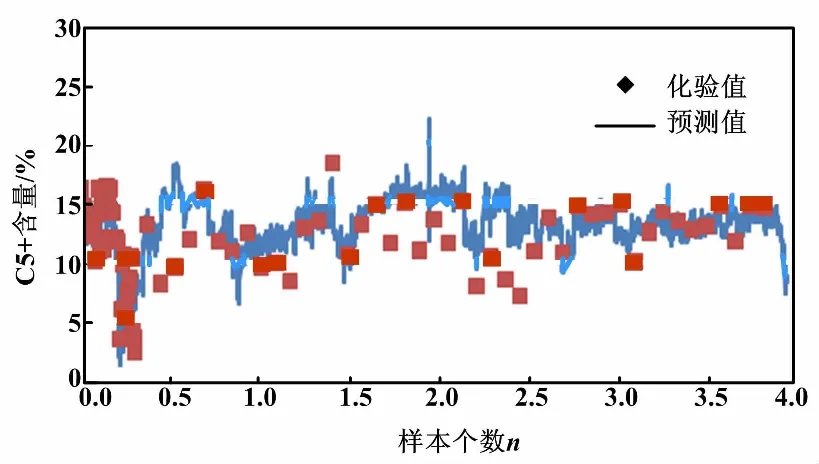
图4 软测量模型在线预测效果图
数据表明:软测量结果能够准确地预测产品质量的趋势,在实际应用中可以逐步取代化验数据,达到降低化验频次的要求。
4 结束语
软测量技术可以实现组分和物性等特殊变量的在线监测,代替在线分析仪表为过程控制提供关键参数
信息。软测量模型结果更常见的用法是直接作为被控变量用于多变量预测控制。随着计算机和信息技术的发展,推断控制策略将越来越多地应用于实际装置并为生产实现节能增效。软测量技术作为智能炼厂建设的重要的技术手段,必将推广到更多的应用领域。
