蒸气动力系统的运行优化研究与应用
2018-08-17林雪茹胡城煌侯卫锋
李 达,林雪茹,胡城煌,侯卫锋
(浙江中控软件技术有限公司,浙江 杭州 310053)
0 引言
大型用能企业,如炼油、炼化、化工、冶金、造纸等企业通常配备了热电联产装置,即蒸气动力系统。蒸气动力系统在为生产工艺装置提供蒸气、电力等能源的同时,自身也消耗大量的能源,在企业的能源消耗中占有较大的比重[1]。目前,国内大部分配备蒸气动力系统的工业企业主要依靠经验来实施系统的运行计划与调度,对运行计划与调度方案的优化研究还远远不够。
国内外众多学者一直在对蒸气动力系统调度优化进行研究。早在20世纪80年代,Grossmann等[2]用混合整数线性规划模型(mixed integr linear programming,MILP)率先研究了蒸气动力系统的优化调度,对蒸气动力系统的参数进行优化。Zhang X等[3]研究学者对该类混整模型引入了调度执行时间的决策,并将此类问题升级为混合整数非线性规划(mixed integer nonlinear programming,MINLP)问题。近年来,国内研究学者也主要基于上述方法对蒸气动力系统进行研究。张冰剑等[4]采用MILP模型来描述蒸气动力系统的超结构,并在研究中考虑设备的停产维护。张鹏飞等[5]考虑了环境污染指标,建立了多目标混合整数线性规划(multi objective mixed integer linear pogramming,MOMILP)模型。另外,蒸气动力系统中设备模型的研究也是当前热点。Varbanov等[6]对于汽轮机、燃气轮机的模型进行了优化与改进,提升了优化空间。鄢烈祥等[7]考虑了锅炉效率的非线性问题。张国喜等[8]研究了汽轮机的非线性做功过程。
1 优化调度数学模型
1.1 目标函数
本模型综合考虑了煤价、外购电峰谷电价及系统凝汽发电支出等价格与成本数据,并由此建立了系统的目标函数。目标函数为:
(1)
式中:Z为蒸气动力系统的能源消耗总费用,元;Ccoal为原煤价格,元/h;Fci为第i台锅炉进煤量, t/h;Cp为外购电价格,元/kWh;P为外购电量,kW;Ccds为凝汽发电支出费用,元/kWh。
模型的约束条件可分为以下几类。
(1)物料平衡约束。
∑Fi,in-∑Fi,out=0
(2)
式中:Fi,in为设备i进口物料,t/h;Fi,out为设备出口物料,t/h。
(2)能量平衡约束。
①锅炉能量平衡。
ηi=f(FSi)
(3)
式中:ηi为锅炉i效率;FSi为锅炉i产汽量,t/h;f为锅炉效率与产汽量关系插值函数。
依据锅炉运行数据,锅炉效率与产汽量关系函数采用分段线性插值方式获得。
②汽机能量平衡。
Wi=f(Fti,Ft1i,Ft2i,Ft3i)
(4)
式中:Wi为汽机i发电功率, kW;Fti为汽机i进汽量,t/h;Ft1i为汽机i1级抽汽量,t/h;Ft2i为汽机i2级抽汽量,t/h;Ft3i为汽机i排汽量,t/h;f为汽机发电功率与进汽量、抽汽量关系模型函数。
依据汽机运行数据,采用数值拟合方法建立汽机发电功率与进汽量、抽汽量的关系模型。针对汽机在变工况下的特性曲线具有非线性的特点,为了提高汽机模型的精度,采用分区线性化方法,将汽机发电功率与抽汽量分成若干区后再作线性化处理,得到通用汽机模型公式:
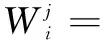
(5)
式中:a、b、c、d、e为公式拟合参数;j为所分区间,j=Ⅰ,Ⅱ,Ⅲ。
③凝汽式汽机发电成本。
(6)
(3)能力约束。
①设备进出物料流量约束为:
Fi,in,min≤Fi,in≤Fi,in,max
(7)
Fi,out,min≤Fi,out≤Fi,out,max
(8)
式中:Fi,in,min、Fi,out,min分别为汽机i进、出口流量最小值, t/h;Fi,in,max、Fi,out,max分别为汽机i进、出口流量最大值, t/h。
②汽机做功能力约束。
Wi,min≤Wi≤Wi,max
(9)
式中:Wi,min、Wi,max分别为汽机i发电功率最小值与最大值,kW。
(4)需求约束。
①电力需求平衡约束。
∑Wi+P≥PDem
(10)
式中:PDem为电量需求,kW。
②蒸气需求平衡约束。
(11)
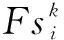
(5)设备效率约束。
ηi,min≤η≤1
(12)
式中:ηi,min为设备i最小效率值。
1.2 锅炉效率模型
①锅炉反平衡效率为:
ηF=100%-(q2+q3+q4+q5+q6)
(13)
式中:ηF为锅炉反平衡热效率;q2为排烟热损失;q3为化学不完全燃烧热损失;q4为固体不完全燃烧热损失;q5为散热损失;q6为灰渣物理热损失。
②锅炉正平衡效率为:
(14)
式中:ηz为锅炉反平衡热效率;D为主蒸气流量,t/h;hs为主蒸气焓值,kJ/kg;hw为锅炉给水焓值,kJ/kg;B为锅炉给煤量,t/h;Qr为单位燃煤所放出的热量,kJ/kg。
采用非线性规划算法对上述模型进行求解,求解算法可参考相关文献。
2 应用实例
某企业的蒸气动力系统由8台锅炉、8台汽机构成,如图1所示。其中:4#~7#锅炉的生产负荷为75 t/h,8#~11#锅炉的负荷为130 t/h;4#、8#汽机为凝汽式汽轮机组,5#、6#、7#、10#、11#汽机为抽背式机组,9#汽机为背压式机组。该系统产出3个压力等级蒸气,压力等级分别为3.6、1.0以及0.4 MPa。锅炉的燃料均为原煤,原煤价格为750元/t,电价为1.08元/kWh。

图1 蒸气动力系统示意图
锅炉效率由上述模型计算,对应的产汽量数据由仪表实际测得。以近3年锅炉实际运行数据为参考,可根据Lagrange插值方法获得锅炉效率与产汽量关系函数式。
4#~11#汽机模型以近3年实测数据为参考,对数据进行筛选整理,经多元线性拟合得到如下方程。
(15)
(16)
(17)
(18)
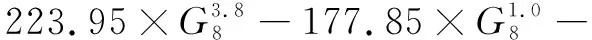
(19)
(20)
(21)
(22)

用户在某一时期对蒸气、电力的需求为1.0 MPa、0.4 MPa,则对应的蒸气需求量分别为51 t/h、336 t/h;电力的需求量为48 MW。
结合现行调度模式对系统进行优化(即已知某些台设备运行,优化计算该部分设备的负荷得到相应的运行参数),将优化计算得到的结果与实际运行参数进行对比,如表1、表2所示。表2中,P0、P1、P2、P3分别表示8.9 MPa、3.8 MPa、1.0 MPa、0.4 MPa压力等级。由表1可知,优化后8#~11#锅炉负荷由102 t/h、107 t/h、116 t/h、123 t/h调整为109 t/h、117 t/h、112 t/h、129 t/h。由表2可知,优化后4#~11#汽机发电负荷由0 MW、6 MW、0 MW、6 MW、0 MW、8 MW、12 MW、12 MW调整为0 MW、6 MW、0 MW、6 MW、0 MW、12 MW、12 MW、12 MW。因此,增大汽机发电总负荷,即可降低外购电量。从蒸气动力系统总的优化策略来看,其原理是增大锅炉组合中效率高的锅炉产汽量,从而在外购电价较高时少购电,并使效率高的汽机多发电。若以这种调度方案下的优化结果为参考,节能效益能达到3.1%,可为企业带来每年1752万元的经济效益,节能效果显著。由此可见,若结合已有调度经验对蒸气动力系统进行操作优化,系统仍有较大节能空间,且这种优化方案有相当大的可操作性,易实施,调度技术人员也易于接受。企业可根据已积累的调度模式与经验,同时结合优化调度技术进行科学调度,提高优化调度水平,提升节能效益。
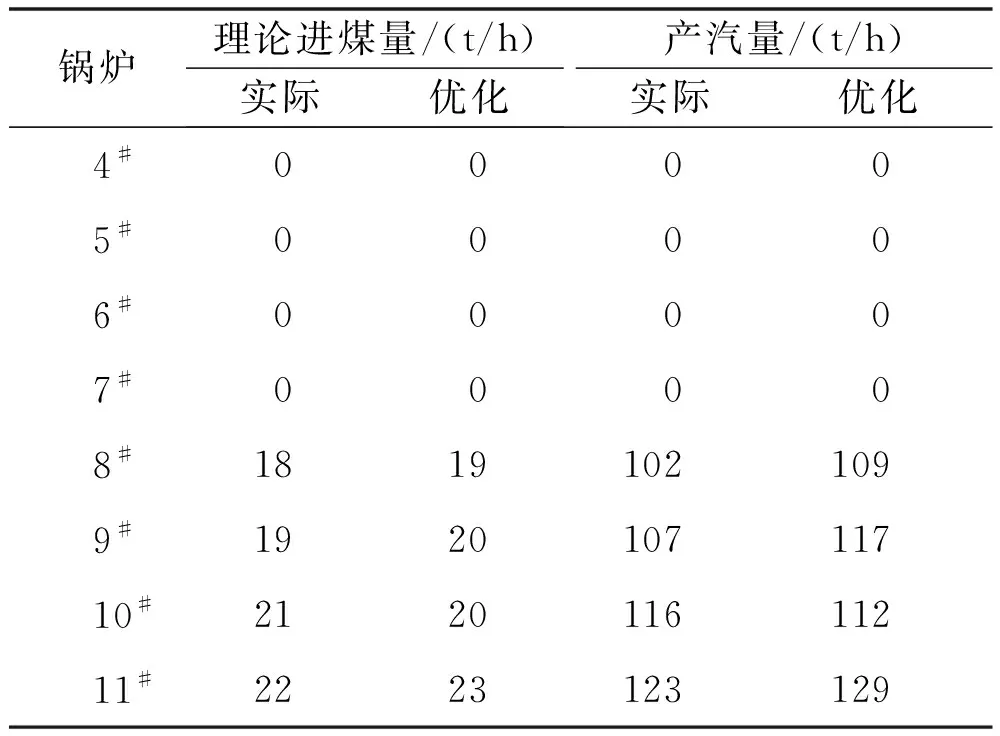
表1 现行调度模式下锅炉系统优化计算结果
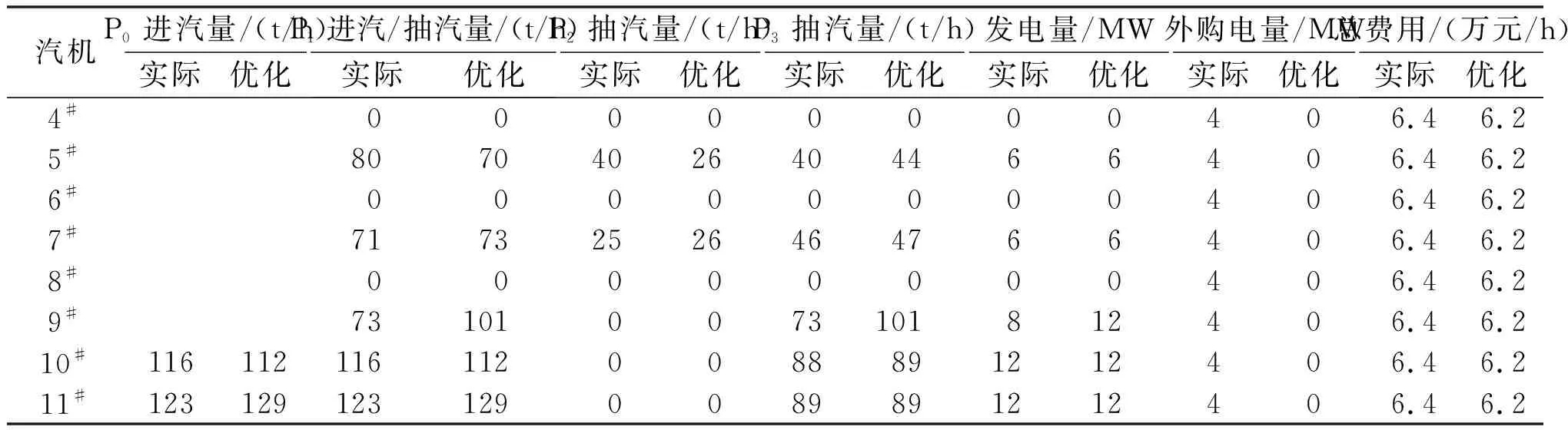
表2 现行调度模式下汽机系统优化计算结果
3 结束语
蒸气动力系统的实际运行过程同理论研究的理想过程相差甚远,存在着诸多的不确定性因素,处理起来非常困难,且方案的可操作性较差。因此,本文从实际应用角度出发,最大程度地吸收了企业现有的、关于蒸气动力系统的调度经验,并将这些经验融入理论研究过程,建立了蒸气动力系统的操作优化模型;利用非线性规划方法对模型进行求解,得到了蒸气动力系统的最优操作参数,由此获得具体的操作方案。该方案契合企业实际情况,具有很强的可操作性,能有效指导企业降低生产与调度成本。
