条件技术下静态内模控制抗饱和框架稳定性分析

李海霞

(忻州师范学院 电子系，山西 忻州 034000)

0 引言

饱和非线性问题在工程学控制系统中无处不在[1]，是控制系统中最常见的一种非线性.饱和现象的本质是控制器的输出与被控对象的输入信号不相等了[2]，系统完全处于“失控”状态.根本原因是执行器的物理装置无法做到控制器输出信号要求的动作.因此，饱和问题不可轻视，否则可能会引发灾难性的后果.回避饱和、不适当地降低控制器增益，将导致系统性能下降[3].因此，采用适当的方法进行抗饱和设计可以解决控制系统出现的饱和现象，进而确保系统的安全稳定运行.现存的抗饱和控制方法大体可以分为两种[4]：一种是在控制器设计初期就将饱和因素考虑进去，这种方法计算复杂繁琐；另外一种方法是将控制器的输入信号和输出信号的偏差作为反馈信号，采用一定的补偿算法予以消除，条件作用技术[5]属于后者，本文将进一步分析基于条件技术的内模控制抗饱和框架的稳定性问题.

1 控制系统中的饱和现象

饱和的本质是执行器的输入信号不等于输出信号.典型的饱和非线性如图1所示.

图1 饱和非线性

饱和现象可以用数学函数描述为：

通过仿真下面的这个实例可以说明饱和现象是如何造成系统性能恶化的.被控对象为：

(1)

受限的闭环PID控制系统框如图2所示.

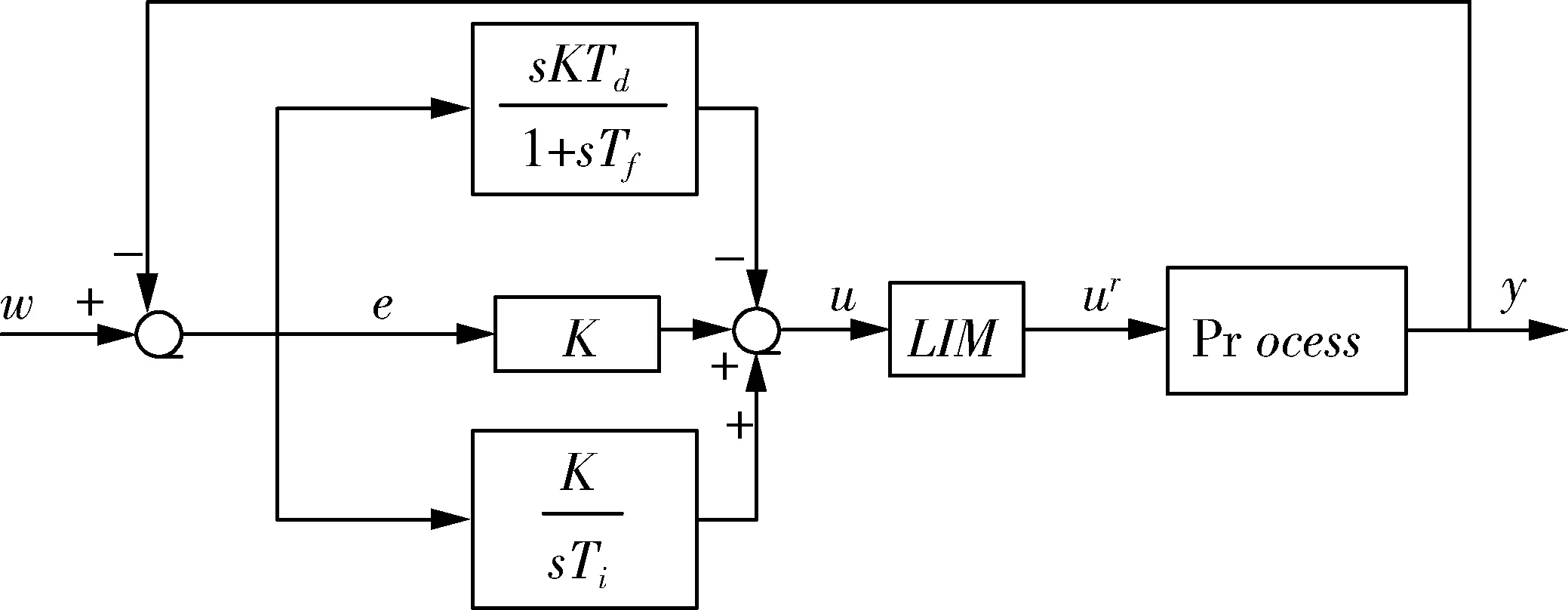
图2 输入受限的闭环PID控制系统框图

K=20，Ti=30 s，Td=0.95 s，Tf=0.095 s

输入上限为：Umax=2，输入下限为：Umin=0，图3为闭环系统阶跃输出响应，其中实线为没有输入限制时的输出响应曲线，点线为输入出现限制，输出饱和时的响应曲线.图4为被控对象输入信号的曲线.其中加粗的实线是未加输入限制的被控对象输入信号曲线，点线是加了输入限制后，被控对象的输入信号曲线.

从图3中，可以很明显地看出，当系统输入受限时将会在原来没有受限系统的基础上出现很大的超调量和调节时间.这种由于输入受限而导致的闭环响应性能急剧恶化现象就是饱和现象.

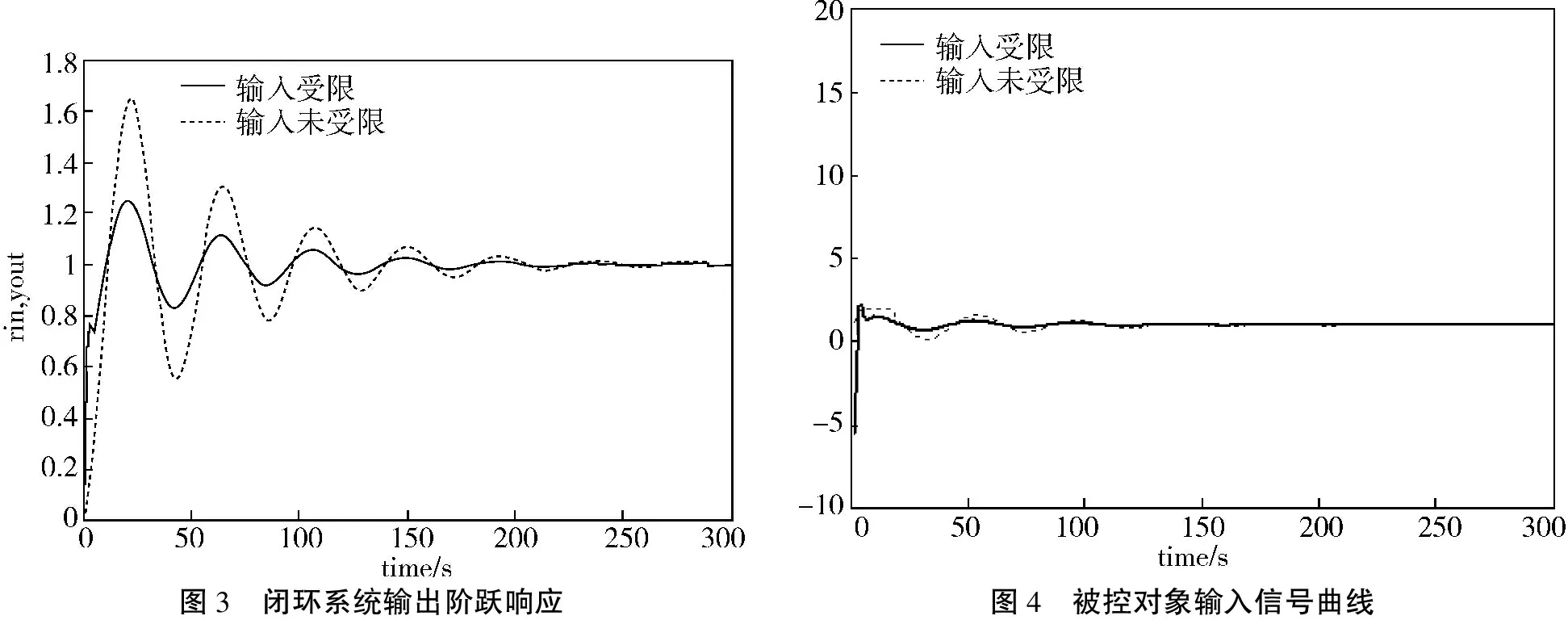
图3 闭环系统输出阶跃响应图4 被控对象输入信号曲线

2 基于条件技术的内模控制抗饱和控制器设计

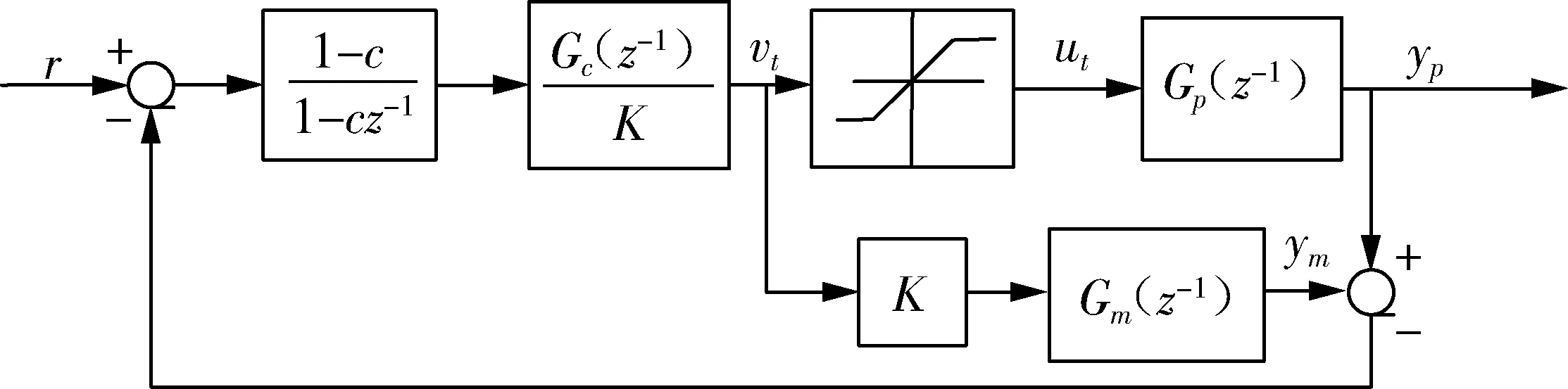
图5 静态内模控制抗饱和框架

在过去的20年里，内模控制在过程和系统控制中变得越来越流行了，原因是内模控制结构对于干扰和不确定性有很强的鲁棒性.同时内模控制还为线性和非线性系统分析全局稳定性提供了依据.在使用内模控制结构时，唯一受限的是需要保证被控对象开环稳定和最小相位.内模控制在处理输入饱和现象方面，相比较内模控制在鲁棒控制中的应用，是相对稀少和罕见的.在早期的文献[2]和[6]中指出，人们从来没有试着用内模控制结构来作为抗饱和控制的框架，然而在文献[7]和[8]中，首次提出内模控制能够用来解决抗饱和的问题.同时，文献[8]还给出了一个实例，证明了内模控制具有内在的抗饱和特性.文献[10]用改进的内模控制抗饱和方法对一个不稳定的被控对象进行了分析和设计.文献[11]针对一个化学反应容器的单输入单输出系统，提出了内模控制处理非线性系统的一些规律.值得一提的是Chung Seng Ling等人在2004年提出的一种静态抗饱和方法，避免了当时非常流行的抗饱和补偿控制框架的复杂性，同时还能确保所有的输入输出受限系统的全局稳定性.他们的内模控制抗饱和框架如图5所示[2].

图5所示的框架中，KGm(z1)为内模控制器，饱和非线性环节与Gp(z-1)一起作为了内模控制器的被控对象，内模控制的最终效果是控制器的模型逐渐逼近被控对象，设计的初期，一般都设计成Gm(z-1)=Gp(z-1)，通过不断调整K值大小，使得控制器输出和被控对象的输出差值逐渐减小，最终实现了抗饱和的目的.

滤波器设计如下[6]：

(2)

其中，0≤c<1，是待选择的.添加滤波器的目的还为了使被控对象模型的逆存在且可实现.增益K的选择决定了系统在饱和影响下系统的性能.调整K的大小的规则是首先选择一个足够大的K，使得执行器处于极限位置，然后再逐步调小K，提高系统的响应速度直到系统出现超调.

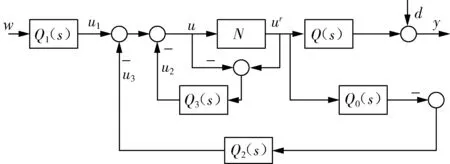
图6 条件技术下静态内模控制抗饱和框架

条件技术本质是通过重新计算参考输入信号来消除u-ur的偏差[5]，将饱和非线性环节转移到了参考输入信号中，从而实现抗饱和.通过重新计算参考输入，使得控制器在不进入饱和区的同时跟随新的参考输入量，这就保证始终有u=ur，从而消除了饱和现象.重新计算的参考输入信号可以表示为“可行的参考输入”(wr)：当它代替实际的参考输入信号w输入控制器时，控制器的输出信号u和被控对象的输入信号ur会立刻相等.文献[1]利用条件技术和内模控制设计了条件技术下静态内模控制抗饱和框架，并给出了框架中内模控制器和抗饱和控制器的设计，如图6所示.

其中，Q3(s)的设计利用条件技术思想，Q2(s)用来消除内模控制中理论模型G0(s)与实际模型G(s)的偏差.Q1(s)属于前馈控制器，用来跟踪参考输入信号.文献[6]同时给出了三个控制器的计算公式：

Q3(s)=1-K*Q1(s)

文献[1]用两个串联的巴特沃斯滤波器作为被控对象，本文拟采用被控对象数学模型为：

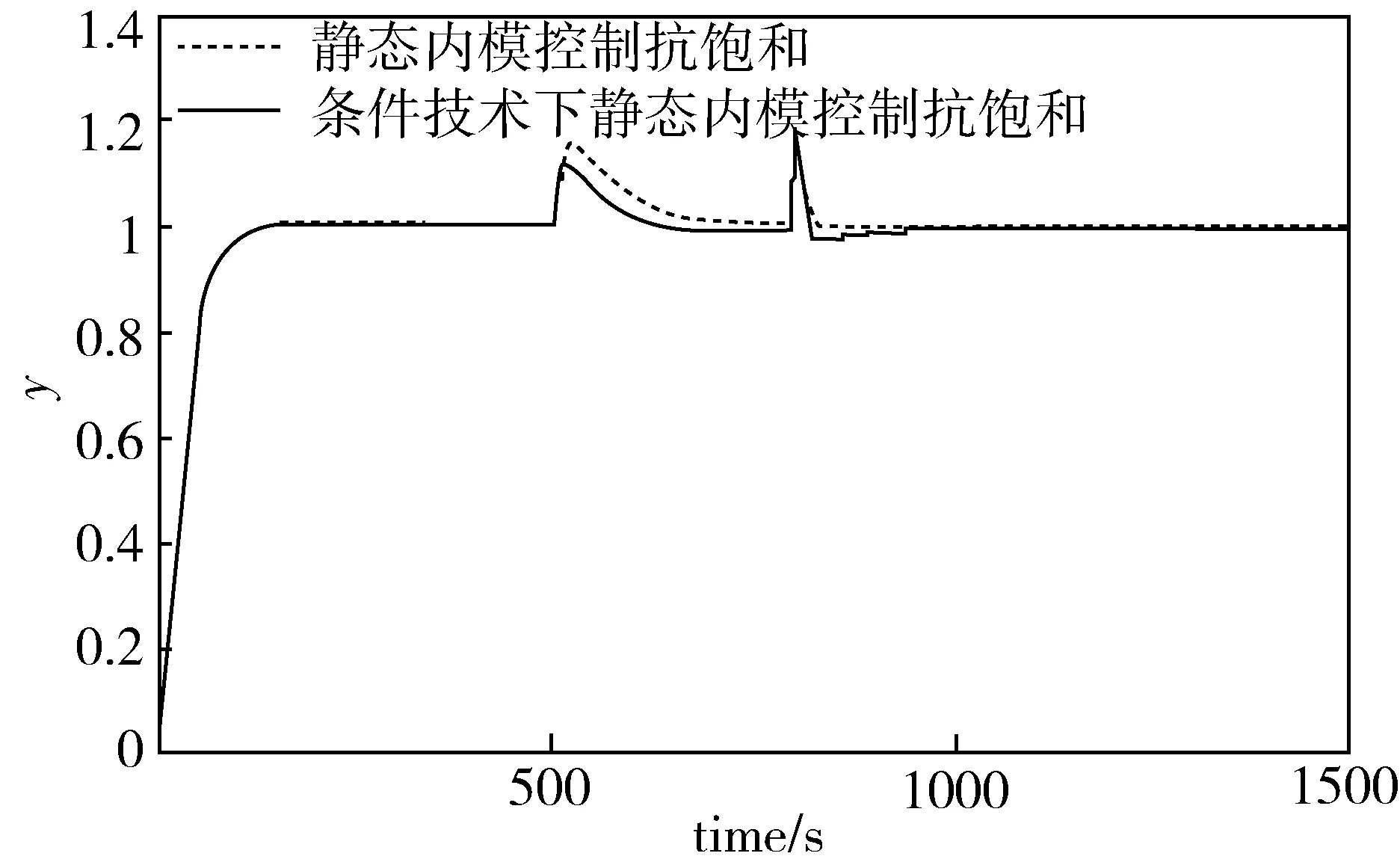
图7 输入受限系统的闭环输出响应

被控对象输入限制在±1，图7为t=0加参考输入r=1，t=500加输入干扰di=1，t=800加输出干扰d0=0.2时的输出响应曲线.实线为三自由度内模抗饱和控制系统的闭环输出响应.

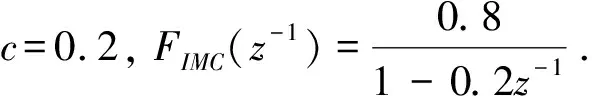
3 静态内模控制抗饱和框架的稳定性分析

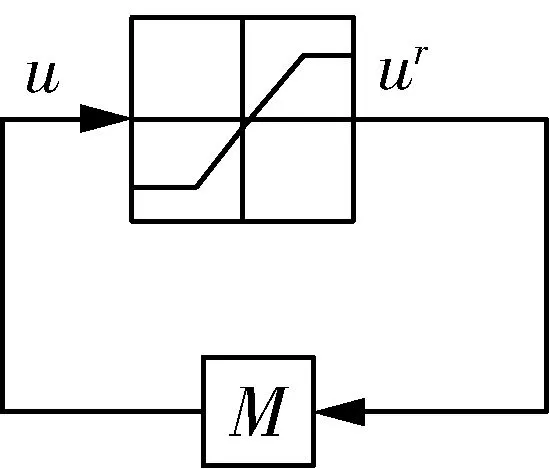
图8 结构变换-线性函数和非线性子系统反馈连接

对于传统的内模控制系统，只要模型和对象完全匹配，闭环系统就能保持全局稳定[7].图5所示的系统可以等价转换为只有两个子系统通过反馈连接的系统.其中一个子系统是动态线性传递函数，另外一个子系统是静态饱和非线性，如图8所示.动态线性传递函数可以用不饱和信号vt和饱和信号ut的比值来确定：

(3)

从图5中，可以得到以下这些方程：

yp=Gput.

(4)

ym=KGmvt.

(5)

由于参考输入信号r不影响闭环增益，所以未发生饱和的信号vt的推导如下：

(6)

将等式(4)和(5)带入等式(6)可得：

(7)

假设模型和对象完全匹配，即Gp=Gm，Gm-1Gp=1，那么等式(7)可以重新写为：

vt=-FIMCK-1ut+FIMCvt.

(8)

所以，

(9)

考虑一个反馈支路上带有非线性的单输入和单输出非线性系统，如图5所示.

Ψ(.)处在反馈支路，为一个一维时不变，无记忆非线性，G(z-1)是一个严格满足Hurwitz稳定的传递函数.Popov稳定性判据给出了一个判断系统渐进稳定的充分条件.若Ψ(.)∈(0,1],且满足以下不等式：

Re[(1+jw)G(jw)]>-1,∀w≥0.

(10)

方程(10)可以被重新写为：

Re(M(jw))+wIm(M(jw))>-1,∀w≥0.

(11)

定义N，

(12)

从Popov稳定性判据中可以推导出以下新的稳定性判据：

对于图5所示的内模控制抗饱和框架，对于任意选取的K和c，当出现饱和时，只要能满足Re(N(e-jwt))>0，且对于任取的w≥0，都有Im(N(e-jwt))=0，则内模控制抗饱和系统是全局渐近稳定的.

(13)

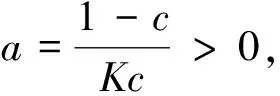
(14)

所以可以得到：

∀w≥0.

(15)

从式(15)可以得出图5所示的内模控制抗饱和系统在所有的大于零的频率下都是鲁棒稳定的.在K>0,0

4 结论

本文在详细分析饱和现象发生的本质原因的基础上，通过仿真说明饱和现象给控制系统带来的灾难性后果.利用静态内模控制抗饱和框架和条件技术设计了条件技术下静态内模控制抗饱和框架，通过仿真进一步验证了条件技术下的静态内模控制框架的抗饱和效果优于单独采用静态内模控制抗饱和框架.同时利用Popov稳定性判据对静态内模控制抗饱和框架的稳定性进行分析，最终证明静态内模控制抗饱和框架的全局渐进稳定性.