考虑油膜动力学响应的船舶轴系轴承稳态负荷求解方法
2018-08-17温小飞周瑞平雷俊松
温小飞,周瑞平,袁 强,雷俊松
(1.武汉理工大学能源与动力工程学院,湖北武汉 430063;2.浙江海洋大学港航与交通运输工程学院,浙江舟山 316022)
船舶轴系轴承在运行工况常因轴承负荷变化而导致漏油[1]、轴承发热等问题,但一直以来相关船舶规范文件[2-3]中均对运行工况的轴承负荷做出明确要求或限制。在相关研究方面,1992年徐龙祥等[4]考虑了轴承油膜的非线性弹性影响用传递矩阵建立了大型汽轮机发电机组轴承负荷分配计算方法,王刚志等[5]认为精确的润滑计算应采用连续梁轴承载荷计算方法,周瑞[6]建立了舰船推进轴系校中多目标优化模型对轴承负荷进行计算,程鹏[7]提出以示功图为输入条件计算出不同的曲柄转角下其连杆大端轴承和主轴承的负荷,彭泽军[8]建立了大型汽轮发电机组轴承负荷分配计算的矩阵方程对轴承负荷进行了计算与分析。总体而言,船舶轴系轴承负荷计算方法一般仅考虑油膜刚度(且为常数)的影响,而很少考虑轴承油膜动力学响应(动态),主要原因在数学模型、计算方法等方面构建的困难程度,因此本文将针对该问题提出考虑油膜动力学响应的船舶轴系轴承稳态负荷耦合计算方法,为稳态轴承负荷计算提供方法。
1 船舶轴系轴承稳态负荷耦合数学模型
在船舶轴系稳态运行状态,船舶轴系-轴承系统以油膜为介质实现了力学平衡,同时又通过各轴承轴颈位置关系达到了轴承负荷重新分配和再平衡,因此船舶轴系轴承稳态负荷耦合数学模型可表示为式(1),其中包含了几何耦合关系和力学耦合关系。

式中,R为轴系轴承负荷矩阵,Ceff为轴承影响系数矩阵,R0为轴系轴承的热态负荷矩阵,可通过船舶轴系校中计算方法直接求解;F 为轴系轴承油膜力矩阵,Z 为轴系轴承稳态位置矩阵,Fe,i、Fφ,i、φi、Zi、ci、εi分别是第i个轴承的偏心方向油膜力、垂直方向油膜力、偏转角、轴颈中心位置、轴承间隙、偏心率等,且均可应用油膜动力学方程和边界条件,通过迭代求解得到。
2 混合求解计算流程设计
根据式(1)所包含数学模型的物理含义和数学求解方法,将船舶轴系轴承稳态负荷计算过程分解为三个子模块,分别为轴系校中计算模块、油膜动力学求解模块和耦合求解模块,其中轴系校中计算模块和耦合求解模块均为解析求解,而油膜动力学求解模块为迭代求解。三个子模块之间通过数据流进行耦合,其中轴系校中计算模块计算结果分别传递至油膜动力学模块和耦合求解模块,Ceff传递至耦合求解模块;同时,耦合求解模块除了耦合处理其他两个模块计算结果外还将结果反馈到油膜动力学模块并进行新的迭代求解,如图1所示。

图1 模块间数据流示意图Fig.1 Diagram of data flow among modules
3 子功能模块设计与处理
3.1 船舶轴系校中计算模块
船舶轴系可简化为超不静定梁问题,且假设船舶轴系两端均为自由端,则船舶轴系校中计算数学模型可以通过式(2)表示。

式(2)中 Mi、Pi、Zi、Ci分别为第 i节点的弯矩、集中力、轴承位置值和设定轴承位置值,Ii、Li、Ei、qi分别为第i单元的截面惯性矩、长度、材料的弹性模量和均布力。求解得到Mi值,通过式(3)即可计算得到轴系各轴承负荷Ri。

通过MATLAB编程技术,设计了船舶轴系校中计算模块流程如图2所示,其包含了几何及物理模型数据库文件bearing_data_model.xlsx,以 EXCEL 格式文件通过函数“xlsread”读至计算程序,同时为了使程序具有更好的移植性,并结合实际计算需要编写一系列自定义函数:几何建模函数dimension_b()、截面惯性矩计算函数I_cal()、弯曲刚度计算函数EI_cal()、均布力计算函数q_cal()、系数矩阵A构建函数A_matrix_b()、系数矩阵C构建函数C_matrix_b()、轴承负荷计算函数bearing_F_cal()等。在自定义函数基础上,根据式(2-21)编制代码 X_matrix=(A_matrix)^(-1)*C_matrix,计算得到轴系各截面的弯矩值和挠度值,最终得到R0和Ceff。
3.2 油膜力计算模块
油膜力计算模块中采用了无量纲化的滑动轴承油膜动力学数学模型即式(4)和Sommerfeld边界条件即式(5)。通过数值计算可求解得到无量纲压力P在θ和Y上的分布规律,在获得求解域内的压力分布后,即可进行油膜稳态工况其他特征参数求解。

图2 船舶轴系校中计算模块流程图Fig.2 Flow-process diagram on calculation module of ship shafting alignment
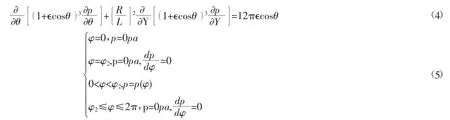
式(4)和式(5)中P、Y、ϵ分别表示无量纲压力、长度和偏心率,θ为偏转角,φ周向角度,φ2为油膜破裂周向角。
轴承油膜力计算模块以船舶轴系校中热态轴承负荷、轴承几何参数、润滑油物性参数、轴转速等作为输入计算参数,以EXCEL文件形式保持,通过函数“xlsread”读至计算程序,计算后得到油膜力、偏心率和轴颈位置数据;在模块中包含了一系列自定义函数:轴承参数构建函数bearing_para_b()、单轴承油膜动力学参数计算函数single_bf_cal()、油膜力粗算函数F_cal()、油膜压力分布计算函数dispressure()、作用力积分函数totalpressure()、油膜力精算函数Fnext_cal()等,具体流程如图3所示。
由于油膜力计算精度与偏心率变化幅值数量级大小相关,若选择不合适,将导致数据结果振荡而无法收敛,为了解决这个问题,本文采用了逐级降低偏心率变化幅值数量级方法,实现了快速收敛计算并保证了计算精度。
3.3 耦合求解模块
耦合求解模块是以船舶轴系校中计算模块和油膜力计算模块的计算结果为基础,根据油膜力和轴承负荷差值及其大小关系,确定偏心率微调策略,通过循环迭代最终达到轴系轴承负荷与油膜力的基本相等,以其误差设定值(本文设定值为200 N)为收敛判据,其具体流程如图4所示。在耦合求解模块中除了调用其他两个模块数据外,还需反复调用两个函数:油膜力计算调用函数F_e_cal()和轴承负荷计算函数Rnext_cal()。
耦合求解模块关键问题是步长选择与收敛判据的问题,本文首先对轴系轴承负荷与油膜力差值的绝对值进行大小排序,借鉴船舶轴系合理校中计算的轴承变位调整思路,选择其中差值最大的两个轴承进行轴颈偏心率微调量作为求解步长,以前后迭代值之差作为收敛判据。由于实际差值有可能为“正”或“负”,因此对应偏心率调整也具有方向性;若轴承负荷差值为正,则其对应轴颈偏心率将增加一个偏心率增幅即“delt_e”,反之则减小一个偏心率增幅。同时为了提高收敛速度和计算精度,轴颈偏心率增幅即求解步长,根据前后两次迭代值之差进行数量级调整即当“delta_FR”大于2 000 N时求解步长为0.001,随着“delta_FR”下降至2 000 N时求解步长为0.000 1,进一步“delta_FR”小于1 000 N时求解步长调整为0.000 01。

图3 油膜力计算模块流程图Fig.3 Flow-process diagram on calculation module of oil film force

图4 耦合求解模块流程图Fig.4 Flow-process diagram of the coupling calculation module
4 计算结果分析与验证
以某64 000 DWT散货船为例对船舶轴系轴承稳态负荷耦合计算方法进行分析,船舶轴系轴承稳态负荷计算过程涉及到轴承、轴颈几何尺寸及长细比等参数,见表1,表中包含了8个轴承及其相应轴颈的基本几何尺寸,依据长细比分类原则,除了尾轴承为长轴承外,均为有限长轴承,“*”表示等效直径。船舶轴系轴承稳态负荷计算除与轴颈、轴承、轴承间隙等几何尺寸相关外,还与轴承润滑油物性参数、工作条件等因素关系密切,根据船厂提供的滑油参数可知正常运行温度为40℃,滑油粘度为0.092 4 Pa.s。
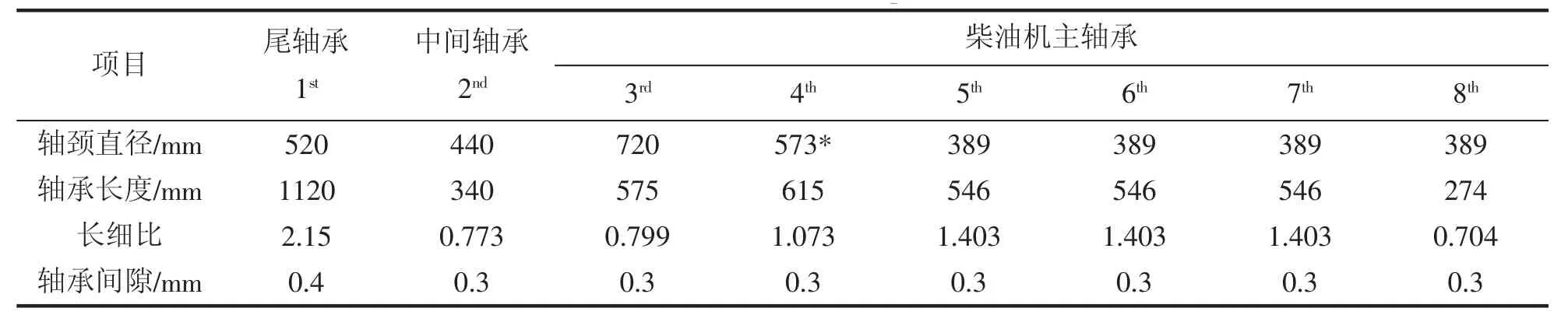
表1 船舶轴系轴承的几何参数表Tab.1 Geometric parameters on bearings of the marine shafting
通过MATLAB计算得到轴系轴承稳态负荷变化曲线,如图5所示,图中8个轴承稳态负荷随着转速变化而变化,其中1号轴承(尾轴承)稳态负荷随着转速升高略有下降、中间轴承稳态负荷随着转速升高逐渐增大,而主机主轴承稳态负荷有部分增加、有部分减小。这些轴承负荷变化曲线与传统轴系校中计算得到轴承负荷为定值在变化规律上体现已是完全不同,体现了船舶轴系轴承负荷在轴承油膜动力学响应影响下轴系轴承重新分配的特征
为了验证数学模型和计算程序,进行了实船试验并整理得到2号轴承横向间隙变化的实测数据,并与理论计算值变化曲线进行了比较,如图6所示。通过比较分析可得:中间轴承横向间隙的测量值与应用船舶轴系轴承稳态负荷耦合数学模型计算后得到的理论值基本吻合,验证了本文采用的数学模型、编程思想和计算程序。

图5 轴系轴承稳态负荷值变化曲线Fig.5 Curves on steady load of shafting bearings
5 结语
船舶轴系轴承稳态负荷受到轴系几何结构、船舶运行状态、滑油参数等多重因素的影响,计算过程非常复杂,通过MATLAB编程可根据数学模型及耦合关系较容易地实现了计算和得到了预期结果,并大大节省了计算周期。本计算程序具有通用性,可直接用于船舶轴系校中计算和滑动轴承油膜动力学特性分析,也可延伸到船舶轴系轴承动态负荷计算。
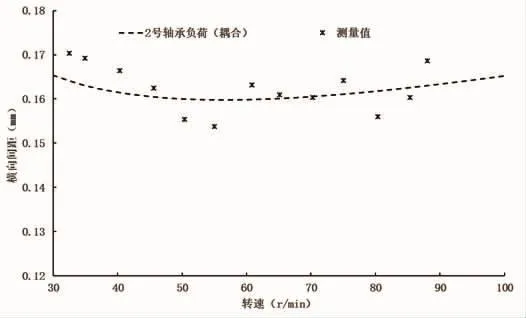
图6 中间轴承横向间隙理论值与测量值比较图Fig.6 Comparison on transverse clearance between theoretical value and measured value
