金融自助终端配钞算法研究

谢卫平 王庆华 谢兴锋

（深圳怡化电脑股份有限公司，广东 深圳 518026）

[关键字] ATM；配钞算法；均空法；平均法；混合面额钞箱

1 引言

金融自助终端配钞是指对ATM机芯中各个钞箱中不同面额的钞票数量进行统筹管理。一般地，金融自助设备装有至少一个钞箱，至少有一种面额，每一个钞箱装有一定数量的相同面额的钞票，设备出钞不但需要考虑满足用户的取款需求，同时还需要兼顾考虑维护人员的加钞维护需求，因此，每次设备出钞时都需要根据用户输入金额进行配钞，还需要对钞箱可用钞票剩余情况进行综合管理。

在自助设备技术领域主要有如下六类配钞原则：

(1)均空法：各个面额的钞票以近乎相同的概率被清空；

(2)平均出钞法：按照各个面额张数近乎相等的配钞方案进行出钞；

(3)大面额优先法：优先出面额大的，按照该种方案出钞，但总张数不一定最小；

(4)小面额优先法：按照总张数最多的配钞方案进行出钞；

(5)最小总张数法：按照各面额出钞总张数之和最小的配钞方案进行出钞；

(6)最大总张数法：按照各面额出钞总张数之和最大的配钞方案进行出钞。

目前，绝大部分自助终端产品采用穷举法技术来实现以上配钞原则，效率太低，弊端明显。也有部分厂商对穷举法进行了改进，如根据货币面额的数值特征进行组合求解，虽提高了配钞效率但不具有通用性，又如文献[1]根据小于所有面额公倍数的残值利用穷举法进行二次配钞的方法，存在不能快速求出所有可行的配钞方案，算法具有不确定性的问题。其他的一些算法，如文献[2]提供的配钞方法时间复杂度高，难以发现各可行配钞方案之间的逻辑关系并进行优选。

本文对现有配钞算法存在的一些技术问题进行了针对性研究，并提出了一种新的配钞算法，解决了现有配钞算法的效率性问题和不确定性问题。

2 配钞数学建模

金融自助设备配钞可分为单一面额钞箱配钞和混合面额钞箱配钞两大类。

2.1 单一面额钞箱配钞

假设自助设备上有n种面额，各个面额的面额值从小到大依次为A1、A2……An，自助设备上各个面额A1、A2……An对应的可用的张数S1、S2……Sn，用户要求的各面额最低需求张数B1、B2……Bn，现需要对配钞金额为M进行配钞，设各个面额 的 配 钞 张 数 为 X1、X2……Xn，则 有 关 系 式 ：A1X1+A2X2+…+AnXn=M ，即

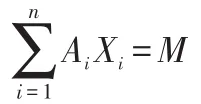
其中 B1≤X1≤S1,B2≤X2≤S2…Bn≤Xn≤Sn

2.2 混合面额钞箱配钞

假设自助设别配备有m个混合面额钞箱，Ai表示第i个混合面额钞箱，Aij表示第i个混合面额钞箱中第j张钞票，表示第i个混合面额钞箱中前k张钞票的总额。

设单一面额钞箱为B，Bi表示第i个单一面额钞箱。设配钞结果为：第i个混合面额钞箱出钞Xi张钞票，第i个单一面额钞箱出钞Yi张钞票。设所述的配钞总额为Total，自助设备有n个混合面额钞箱和m个单一面额钞箱，则有

即

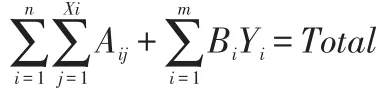
假设对于第i个混合面额钞箱，其前j张钞票的总额为Sij，则有，其中Aik表示第i个混合钞箱中第k张钞票的面额。

则一个序号为i，总计有p张剩余钞票的混合钞箱，可得到一个数组：Si1,Si2…Sik,Si(k+1)…Sip，其中 Si(k+1)=Sik+Ai(k+1)。

3 配钞求解

3.1 单一面额钞箱配钞计算

单一面额钞箱的配钞方法如下：

(1)判断配钞金额是否不大于所述金融自助设备中钞箱剩余金额总数，是则转步骤(2)；否则配钞失败，结束。

(2)求出各面额值的最大公约数，判断各面额值的最大公约数是否可以整除配钞金额，是则转步骤(3)；否则配钞失败，结束。

(3)判断两面额值的最大公约数gcd(A1,A2…An)是否大于1，是则将两边同除以 gcd(A1，A2…An)，得到型如n元一次整系数不定方，其中gcd(a1，a2，…，an)=1，且 M=m·gcd(A1,A2…An)；否则保持原样。

由于 a1，a2，…，an的绝对值都大于1，找出绝对值最小的一个系数，且不妨设a1＞0，则其他系数可以表示为：ai=kia1+ri,0≤ri＜a1(i=2,3,…,n)。此时原方程可转化为：a1(x1+k2x2+…+knxn)+r2x2+r3x3+…+rnxn=M。若a1，r2，r3，…，rn中有某两个互质，则转步骤(5)；若a1，r2，r3，…，rn中任何两个都不互质，再次找出其中最小的系数，将其他系数用该最小系数表示，再次进行转化，一直到有两个互质为止。

其中t,Y3,Y4,…,Yn∈Z。于是就可以求出的解。

(7)根据B1≤X1≤S1,B2≤X2≤S2…Bn≤Xn≤Sn(B1,B2…Bn为用户对各面额的最低需求张数，S1、S2……Sn为各面额的剩余可用钞票数)，由此可以求出整数t的取值范围。

(8)根据配钞原则，进一步限制X1、X2……Xn的值，根据配钞原则的不同，可分为以下几种情况，在[t1,t2]范围内确定t的取值：

a)平 均 出 钞 法 ，此 时 X1≈X2≈…≈Xn，有取最小值；

b)均 空 法 ，此 时 X1-S1≈X2-S2≈…≈Xn-Sn，有取最小值；

e)最小面额优先法，如果Ai是所有面额最小者，Xi尽可能大；

f)最大面额优先法，如果Ai是所有面额最大者，Xi尽可能大。

g)如果是平均出钞法，有 X1≈X2≈X3≈X4，根据有

h)如果是均空法，有 X1-S1≈X2-S2≈X3-S3≈X4-S4，根据取最小值。

i)如果是张数最小法，有(X1+X2+X3+X4)尽可能小。

j)如果是张数最大法，有(X1+X2+X3+X4)尽可能大。

k)如果是最大面额优先法，有X1尽可能大，其次X2尽可能大，再次X3尽可能大。

l)如果是最小面额优先法，有X4尽可能大，其次X3尽可能大，再次X2尽可能大。

m)单一面额钞箱的配钞方案的总种数，还可以采用组合数学中母函数（生成函数）求解，需要用到泰勒基数展开式，可参考文献[6]相关章节，在此不复赘述。

3.2 混合面额钞箱的配钞计算

混合面额钞箱配钞是指：一个或多个钞箱同时存放有两种不同面额情况下的配钞。混合面额钞箱配钞分为两种情况：混合面额钞箱优先法、单一面额钞箱优先法。

3.2.1 混合面额钞箱优先法

假设自助设别配备有m个混合面额钞箱，其要求出钞的优先顺序为A1、A2……Am。假设Ai钞箱有Xi张剩余钞票，假设配钞过程中混合钞箱的出钞数组为D，D1为第一张要出钞的钞票，Di为第i张要出钞的钞票，则对于 Ai(1≤i≤m)，有

得到Am的数组 Sm：Sm1、Sm2…Sm,Xm。

混合面额钞箱优先法配钞算法如下：

(1)令j=1，残值Cj=Total。

(2)在混合钞箱 Aj中的数组 Sj：Sj1、Sj2…Sj,Xj中找出一个最接近但不大于残值Cj的Sji，其中1≤i≤Xj，Xj为混合钞箱Aj中剩余钞票数，如果Sji不存在，转步骤(5)继续进行配钞，否则转步骤(3)继续进行配钞。

(3)计算残值Cj+1=Cj-Sji。如果Cj+1=0，则配钞结束，否则j=j+1继续按照步骤(4)进行。

(4)判断 j≤m是否成立，是则转步骤(2)继续进行配钞，否则按照步骤(5)继续进行配钞。

(5)对步骤(4)所得残值Cj+1用单一面额钞箱按照现有技术进行配钞，配钞成功，流程结束，否则转步骤(6)继续配钞。

(6)对Sji，计算i=i-1，如果 i≥1，则计算Cj+1=Cj+1+Sji-Sj(i-1)，继续进行步骤(5)配钞；否则i＜1，继续按照步骤(7)进行配钞。

(7)对于Cj+1，计算j=j-1，如果 j≥1，则计算Cj+1=Cj+1+Sji-Sj(i-1)，继续进行步骤(5)配钞；否则混合钞箱不参与配钞，只用单一钞箱按照现有技术进行配钞，配钞成功，流程结束；否则配钞失败，流程结束。

3.2.2 单一面额钞箱优先法

单一面额钞箱优先法配钞算法如下：

(1)当配钞总额Total不能被所有单一面额钞箱的所有面额的最大公约数整除时，则按照步骤(2)继续进行配钞；否则按照现有技术进行配钞，配钞成功则流程结束，配钞失败则按照步骤(2)继续进行配钞。此时只有混合面额的钞箱A参与配钞，配钞才有可能成功。

(2)不妨设自助设别配备有m个混合面额钞箱，假设Ai钞箱有Xi张剩余钞票，假设配钞过程中混合钞箱的出钞数组为D，D1为第一张要出钞的钞票，Di为第i张要出钞的钞票。

则对于A1，A2……Am，按照上述混合面额钞箱优先法中的方法，得到Am的数组Sm：Sm1,Sm2…Sm,Xm。

将A1的数组S1各个元素：S11,S12…S1,X1，A2的数组S2各个元素：S21,S2…S2,X2，以及 Am的数组 Sm各个元素：Sm1,Sm2…Sm,Xm，按照从小到大的顺序排列，构成一个数组Sn，其中 n 为对任何1≤i≤j≤X1+X2+…+Xm的正整数i，j，均有Si＜Sj。令i=1，则继续步骤(3)。

(3)计算残值Ci=Total-Si，当Ci不能被所有单一面额钞箱的所有面额的最大公约数整除时，则按照步骤(4)继续进行配钞；否则按照现有技术进行配钞，配钞成功则流程结束，配钞失败则按照步骤(4)继续进行配钞。

举例略。

4 其他配钞算法应用

在实际应用中，可以由单一面额钞箱配钞和混合面额钞箱配钞衍生出多种使用情形。

4.1 总金额非精确法的配钞计算

单一面额钞箱配钞，在实际应用中，有精确配钞法和非精确配钞之分，以下介绍总金额非精确配钞法。

此时，找出一个尽可能小正数△m值，使得gcd(A1，A2…An)可以整除M-△m ，然后按照n=0，1，2…顺序递增，在条件△m+n·gcd(A1，A2…An)不大于允许误差下，求解。直到找出一组合适的解或者△m+n·gcd(A1，A2…An)大于允许误差为止。

4.2 限制面额张数需求的配钞计算

单一面额钞箱配钞，在实际应用中，还有限制面额需求张数与不限制面额需求张数之分。

不妨设自助设备各可用面额从小到大依次为A1，A2…An，各面额的可用钞票数分别为 C1，C2…Cn。

设用户输入的出钞金额为M，对各面额需求的张数分别为不少于B1，B2…Bn，设所求的各面额对应的配钞张数为X1，X2…Xn，最终的出钞金额为M，设自助设备对一切0≤i≤n的整数 i，均有 Bi≤Ci。将方程转化为求，不妨设 Yi=Xi-Bi，则方程转化为

4.3 其他配钞算法

(1)回收钞票数期望最小的配钞法：通过对统计ATM本加钞周期各钞箱的钞票回收率，使得回收率最低的钞箱尽可能地多出钞的配钞方法。该种方法使得回收箱尽可能空，解决了现金业务回收箱瓶颈问题。

(2)限制各面额需求的优化配钞法：如果限制各面额需求时发生配钞失败，在进行配钞计算时，可采取尽可能满足用户面额需求的配钞计算，从而可以向用户提供出钞建议，提高业务成功率和用户满意度。该方法可以细分为大面额需求张数优先满足法、小面额需求张数优先满足法、需求总张数差异最小法、各面额差异均等法等多种情况。

(3)混合面额钞箱发生回收情况下的二次配钞：在混合钞箱出钞时，若发生混合面额钞箱中的某张钞票出钞被回收，则应暂停出钞；根据配钞额度和已出钞总额获得出钞余额；对所述出钞余额继续进行配钞，得到续钞结果；根据所述续钞结果继续出钞。

(4)多个混合钞箱联合配钞法：可先计算出每一个混合钞箱的前i张面额之和，构成一个数组，j个钞箱就会有j个数组。然后利用组合法，从j个数组的每一个数组每次仅取出一个元素，共有j个元素，j个元素之和形成的集合，就是能够成功配钞的总金额。如果要求配钞的总金额不在上述集合中，则无法配钞。

(5)混合钞箱可分离张数的配钞法：即一个或多个混合钞箱联合配钞，采用出钞时故意回收掉极少数几张钞票，剩余出钞的钞票满足总金额的方法，该方法可以提高配钞成功率。

5 结论

本文对金融自助终端的配钞方法进行了研究，建立了各种配钞需求的数学模型并进行了求解，解决了目前ATM技术领域配钞算法时间复杂度过高和算法具有不确定性的弊端，实现了金融自助终端高效率的配钞，本文的研究成果已应用于国内外自助设备10万台级以上，产生了良好的经济效益。