时间序列数据挖掘中的特征表示与相似性度量方法研究分析

王培屹

（郑州幼儿师范高等专科学校，河南 郑州 450000）

1 引言

时间序列数据能够随着时间而变化，它的产生过程极易受环境的影响，而且会伴随一定的噪声。由于数据极为繁杂，研究的难度很大，然而其中蕴含着有非常价值的信息，这类信息对于社会实践具有重要的意义。时间序列数据相较于普通数据而言，它是高维的，在实践过程中，针对时间序列数据，通常都必须对其进行降维，具体方法有两种：其一是进行全局特征分解；其二是局部特征提取。时间序列相似性度量的作用是挖掘时间序列数据中存在的有价值的信息，使其更好地应用于社会生产实践。

2 特征表示方法

时间序列特征表示的含义：针对原时间序列数据，使之转变成另外一个不同论域中的数据，并实现其降维，在进行降维之后，对于低维空间的数据，也能最大限度地反映出原时间序列的信息。就目前而言，已经出现很多特征表示方法，下面就简单介绍几种：

2.1 分段线性表示方法

分段线性表示方法与其他表示方法相比，更加直观和简单，它在时间序列数据挖掘中的应用最为普遍，通常和时间序列相似性度量方法相互配合来使用。利用这种方法来分割时间序列，需要建立线性模型。根据分割方法的不同，采用的分割策略也不同。据分析研究可知，对于滑动窗口方法和自底向上的方法而言，其时间复杂度和序列长度的关系是前者为后者的平方阶；而对于自顶向下的方法而言，其时间复杂度为线性阶。滑动窗口的方法，在某些情形下，对时间序列的拟合程度不够好，对于原时间序列中蕴含的变化信息，不能够全面地反映出来。对于自顶向下方法而言，其时间复杂度虽然相对来说更高一些，然而，在图像处理以及机器学习方面，它的应用极为广泛。通过对时间序列进行识别和扫描，寻找其中的关键性片段，如：波谷和波峰，然后再自顶向下切割。遗憾的是，对于噪声数据，它一样比较敏感。通过对比可知，自底向上方法具有其他方法不具备的两大优点：第一，这种方法的时间复杂度对数据集拥有线性扩展性；第二，在分割大部分时间序列数据集时，它的效果更好。通过对比以上三种分割方法，各有优点和不足，经过研究提出了一种更好的分割方法，这种方法集中了自底向上以及滑动窗口各自的优势，不仅使在线分割得以实现，而且，对时间序列数据的拟合效果也非常好。

2.2 分段聚合近似表示方法

分段聚合近似表示方法(PAA)主要是通过平均分割时间序列并根据各段序列的平均值来表示原时间序列。这种方法以m长度的时间序列为对象，将其切割为w段，每段长度为k，对于该长度为m序列段，用k来表示，压缩比为降维数为w，从而实现降维。若要确定特征序列，离不开k和w，如果k值越大，或者w值越小，那么近似表示该时间序列的效果就越不好，同时也会丢失更多的信息，至于其降维幅度，则会越大；如果k值越小，或者w值越大，则会与上述情况完全相反。所以，实现了近似表示效果的最大化，就不能获得更大的降维幅度，需要权衡利弊，找到两者之间的平衡。在时间序列中，有极大值、极小值等重要信息，而这种方法运用了平均值，从而造成这些重要信息丢失，而且，对于那些均值相同，但形态趋势存在极大差异的序列，这种方法的使用会将它们表示成相同的均值信息特征。因此，相关专家学者对这种方法进行了改进，在表示时间序列的过程中，使用均值的同时，兼顾了分段序列的斜率。结合时间序列自身的特点，将其分为不等长的段，仍然通过均值来反映时间序列的特征，即自适应分段常量近似方法，为找到这种方法的分割点，通过采用动态规划的方法来实现对时间序列的最优化分割，在某些情形下，可以采用贪婪算法进行次优分割，从而使算法的效率大大提高。

2.3 符号化表示方法

符号化表示方法的含义：实现时间序列向字符串序列转换的过程。当挖掘时间序列数据中的信息时，传统挖掘方法局限于定量数据，在分析和解决问题方面存在很大的不足。在数据结构中，字符串具有两大优点：第一，具备特定的数据存储结构；第二，其操作算法速度快。近几年，有很多和字符串有关的算法的应用越来越广泛。对于一些特殊的实际问题，很难用具体的定量数据来反映，而通过字符型数据却能收到令人意外的效果。在符号化表示方法之中，符号化聚合近似表示方法(SAX)属于最具代表性的一种，它是在PAA的基础上，加以改进形成的一种表示方法。这种表示方法先将时间序列平均分为若干段，并实现原时间序列的Z标准化，然后再针对数据空间，将其分为概率相同的几个部分，并以不同字符进行表示，最后获得的均值序列便是用各部分的字符表示的。因为SAX是基于PAA的一种符号化表示方法，所以也拥有着PAA的某些缺陷，因此，相关学者提出了兼顾均值和方差并其转化为符号，实现在二维空间下的符号化表示。

3 相似性度量研究

相似性度量方法的主要作用是：权衡不同对象之间的关系。在挖掘时间序列的过程中，相似性度量发挥着至关重要的作用。

3.1 欧氏距离

假设有时间序列 Q={q1，q2，……qm}和 C={c1，c2，……cm}，如果采用M inkowski距离度量方法，则

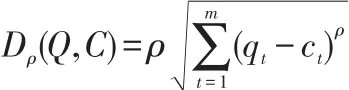
在距离度量方法中，上式是通用的，p值的变化会带来距离度量方式的变化。当p=1时，它表示曼哈顿距离；当ρ=∞时，它转变为 L∞范数，且满足；当p=2时，它表示欧氏距离，它是应用最普遍的一种距离度量方法。通常情况下，若两条时间序列长度相同，欧氏距离可以直接进行距离度量，然而，在大多情形下，它必须同特征表示方法相结合。比如，针对分段之后的时间序列，利用欧氏距离的方法，对拟合序列段直线斜率的相似性进行精密的计算，将时间序列符号化之后，同样利用欧氏距离的方法，在降维空间中，进行相似性度量，在谱分解中进行能量计算，从而使特征序列的相似性度量得以实现。但是，因为欧氏距离对时间序列噪声以及序列段突变有很强的敏感性，对于数据的预处理操作依赖性较强，而且，对于时间序列的位移不能进行有效的识别。最重要的是，它只局限于度量相同长度的时间序列段，针对不同长度时间序列，就不适用。所以，欧氏距离一般情况下，都要充分结合时间序列的特征表示方法来度量时间序列相似性。尤其是在针对特征表示之后的空间进行度量时，一定要满足其下界的要求，避免有所漏报。

3.2 动态时间弯曲

动态时间弯曲的具体含义是：借助弯曲时间轴，来实现对时间序列的匹配映射。它最初的作用是对语音数据进行处理，后来又被用作时间序列相似性的度量。动态时间弯曲在两条时间序列Q={q1，q2，……qm}和C={c1，c2，……cn}之间，寻找出最好的弯曲路径，从而得到DTW(Q，C)，它是最小的距离度量值。只需要符合边界条件的要求，P=(p1，p2……pk)可以用来表示连续性路径，其中，qik与cjk之间的对应关系可以pk表，qik和cjk的弯代价以d(pk)来表示，一般情况下取2，……n，在这一系列弯曲路径中，有一条最优路径可以使弯曲总代价最小，即

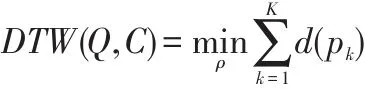
我们可以采用动态规划来构造一个代价矩阵R来求解,即：

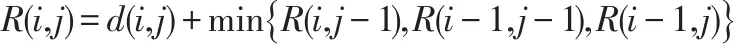
其中，i=1,2,…m ，j=1,2,…n，R(0,0)=0，R(i,0)=R(0,j)=+∞，R(m,n)即动态弯曲时间序列Q和C的最小距离值，即 DTW(Q,C)=R(m,n)。

通过对比动态时间弯曲与欧氏距离，不难发现：（1）前者能够度量的时间序列可以有两种类型，即：长度相同的、长度不同的；后者能够度量的时间序列只有一种，即：长度相同的。（2）针对时间序列的突变点，前者不敏感，而且，也更加适合对其进行度量；后者则不然，针对这类异常时间序列，敏感度较高，不适合对其进行度量。（3）前者能够进行异步相似性比较，后者只局限于同步比较；（4）针对时间复杂度，前者为O(m2)，后者为O(m)；（5）前者不满足三角不等式，后者则满足。

3.3 符号化距离

针对时间序列的特征表示，符号化距离能够将之转变为字符串，转变成字符串之后，其度量方法也随之发生了改变，即由定量数据转变为定性符号。它是在欧氏距离的基础上形成的度量方法，它针对时间序列，做了标准化处理，使之能够满足正态分布，然后再将之转变为字符串。通过查询正态分布图，可以知晓字符间距离。据相关资料显示，这种距离方法也符合下限要求，通过它来搜索时间序列相似性时，可以避免漏报情况的出现。编辑距离的含义是：实现两个字符串之间的转换所须的最少步骤，如删除字符、插入字符等。第一步：将时间序列转变为字符串；第二步：针对两个字符串，借助于编辑距离，度量二者的相似性。编辑距离的主要优点：能够使挖掘算法的性能得到全面提高，更重要的是，对于其具体操作过程，更容易理解和掌握。然而，也存在一些缺点，比如：当两个时间序列不同步时，其相似性度量不能发挥出更好的效果。

4 未来研究方向

随着科学发展的日新月异，我国在时间序列方面的研究也取得了骄人的成绩，被应用于社会生活的各个层面，为社会的发展和经济的建设做出了重大的贡献。比如：在医疗领域中，针对病人群体，可以用来检测其中的异常个体；在金融领域中，可以用来监视消费支出，避免欺诈现象的产生等。但是，在研究的过程中，也逐渐暴露出了一系列的问题，应该给予充分的重视。

分段线性近似表示方法的应用非常普遍，属于最常用的方法之一，它针对时间序列的关键点和关键形态，进行分析和识别，借助于直线段，实现原时间序列的模拟。这种方法的优点是：针对时间序列的特征表示更为直观易懂；它的缺点是：拟合线段数目难以确定。所以，如何有效地对时间序列进行分段线性近似表示是一个非常有意义的研究课题，也将是未来一个重要的研究方向。

动态时间弯曲相对来说伸缩性更好，它可以略过时间序列的特征表示，进行相似性比较。相比于欧氏距离，动态时间弯曲具有两大优势：第一，对异常点没有敏感性；第二，可以度量不等长的时间序列。但是，因为动态时间序列搜索最优弯曲路径的时间复杂度比较高，所以，对于数量多的时间序列，它不适合进行相似性比较，应用范围具有很大的局限性。而且，动态时间弯曲还有一个缺点就是：太过于依赖时间序列数据值，对于局部数据的特征则没有考虑，无法对那些数据相近但形态不同的时间序列进行相似性比较。因此，如何有效提高动态时间弯曲方法的效率和精度是将来的一个重大课题。目前，关于这方面的研究，基本上都偏重于静态时间序列数据，至于动态时间序列数据，研究文献则相对来说比较少。因为动态时间序列数据随时间变化而变化，这就要求特征表示方法和相似性度量方法必须具备高效、稳定的特点。

5 结束语

时间序列是一种应用极为广泛的数据，通过数据挖掘技术能够从中获取有价值的信息，这类信息有助于国家的经济建设，具有非常重要的现实意义。在数据挖掘的过程中，必须做好两项基础性的工作，分别是：特征表示、相似性度量。这两项工作能够为数据挖掘任务提供有效的数据处理方法和技术支持。本文客观地阐述了相关方法的优点和缺点，希望能够为时间序列数据挖掘领域的研究提供帮助。