带预制裂纹的有机玻璃材料断裂强度研究

燕 飞

(北方工业大学土木工程学院，北京 100144)

素混凝土，铸铁，玻璃等脆性材料广泛应用于生活中，工程中也经常需要计算岩体的天然脆性材料的强度。但因脆性材料韧性小，破坏前没有明显的先兆，在外荷载达到极限荷载时会发生突然破坏，常常造成严重的损失，因此有必要研究脆性材料的破坏过程。目前尚无法制得没有任何缺陷的完美材料，因此研究带有裂纹的脆性材料在外荷载下的力学响应和裂纹发展规律就显得十分重要。有机玻璃(PMMA，聚甲基丙烯酸甲酯)因其在室温下呈现脆性，透明度高，易取得和加工，成为了脆性材料研究的理想材料之一[1]。土木工程中也经常采用有机玻璃制作结构模型对结构的性能进行研究。本研究采用带有预制裂纹的开孔有机玻璃板在静态拉伸荷载下的预制裂纹的长度及与开孔的距离对有机玻璃试板强度的影响。国内外学者对有机玻璃材料的断裂进行了大量的研究。吴衡毅等[2]研究了在中低应变率下有机玻璃材料的单向拉伸试验，得出了常温、中低应变率下有机玻璃材料的本构关系，发现随着应变率的上升，有机玻璃材料的抗拉强度上升但断裂能有所下降，在中等应变率下，有机玻璃材料在弹性状态下即发生破坏。于鹏等[3]采用分离式霍普金森压杆试验研究了在高应变率下有机玻璃材料的本构关系，结果表明在常温和高温下，有机玻璃材料在弹性状态下即发生破坏。朱婷[4]采用ABAQUS软件和扩展有限单元法研究了含有预制孔边裂纹的有机玻璃材料在拉伸荷载下的裂纹扩展规律，研究了止裂孔的尺寸对止裂效果的影响。给出了板厚与推荐止裂孔尺寸的关系。李天密等[5]采用自行研制的膨胀环加载装置研究了有机玻璃在高应变率拉伸作用下的断裂行为。孙景辉[1]采用有机玻璃材料制作了粮食筒仓的模型并进行了筒仓壁应力与筒仓中粮食存量的关系，并与采用FLAC3D计算得到的结果进行了对比。

1 试验设计

本研究的试件采用与H.Azadi和A.R.Khoei[6]在其基于流形元方法对有机玻璃材料裂纹扩展模拟的模型相似的试件(模型尺寸见图1)。其后有诸多学者使用其他断裂力学数值计算方法也对上述模型进行了计算，得到的结果与H.Azadi等人的结果相似。但目前尚未有试验研究对上述计算结果进行验证。上述模型没有仅作数值计算使用，因此采用了一端固定，另一端施加位移荷载的方式。考虑到试验过程中试验机夹头对引起的应力分布不均匀和横向约束，无法实现数值计算中的理想边界条件，因此在试验试件的设计中，将试件沿拉伸方向加长，并设置了两个销孔，销孔大于销钉直径且在销钉上涂抹油脂，以确保销钉只提供拉力。为确保加工过程中不会产生裂纹或其他影响试验的缺陷，本试验的所有试件采用激光切割加工。最终的试件图纸见图2。

图2中的a和h为变量，分别代表预制裂纹长度以及预制裂纹至基线(即H.Azadi和A.R.Khoei模型中的边界处)的距离，具体的a和h取值见表1。

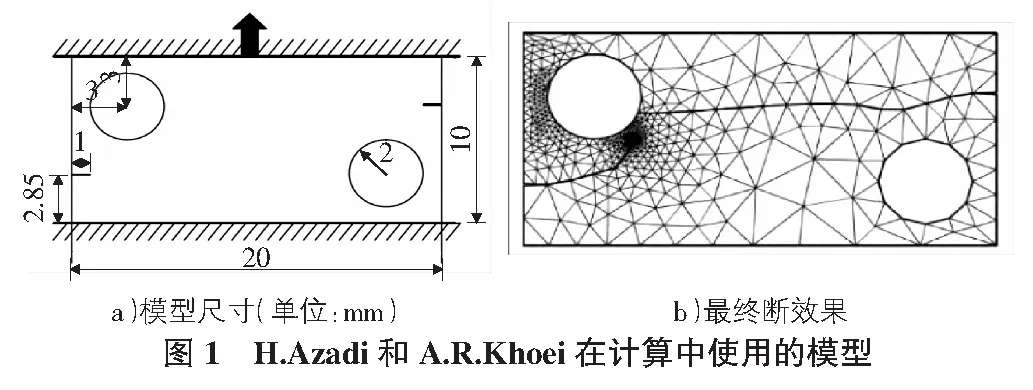
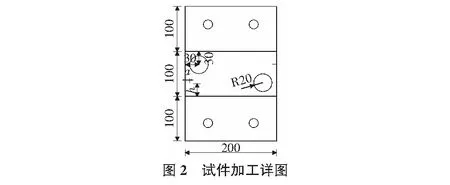
表1 试件尺寸取值

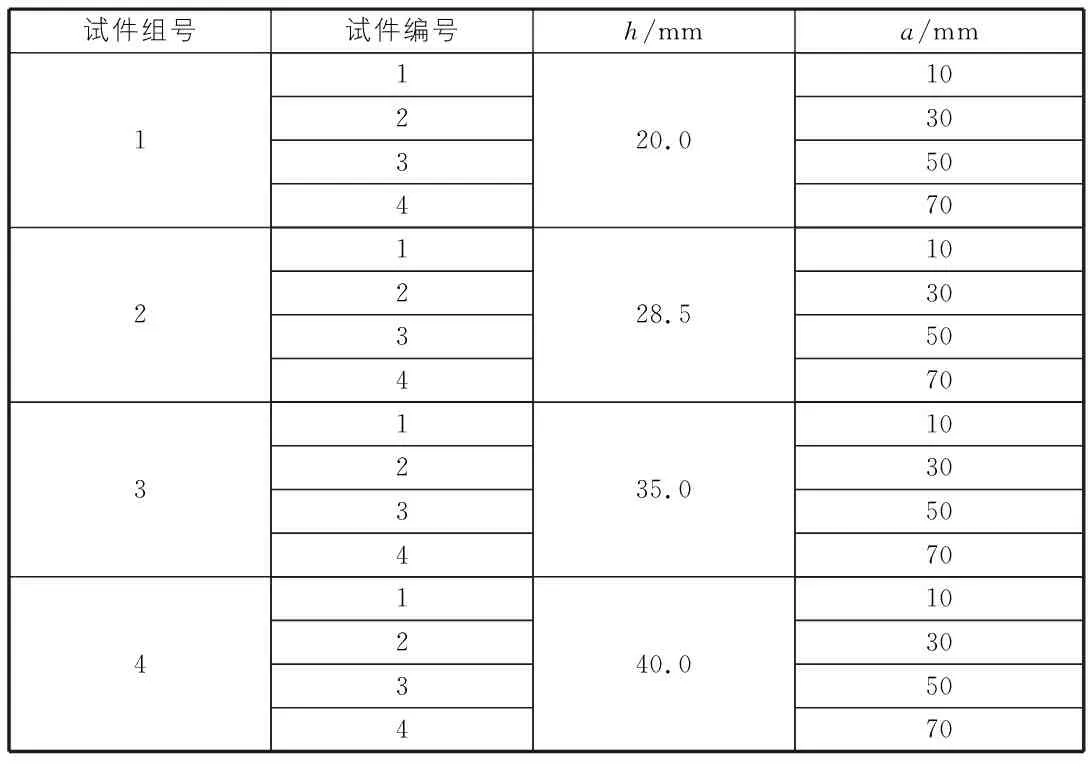
试件组号试件编号h/mma/mm1123420.0103050702123428.5103050703123435.0103050704123440.010305070

2 试验过程

本实验采用Byes3000电子万能试验机匀速加载，加载时上夹头保持不动，下夹头按照预先设定的速度匀速下降直至试件断裂。加载速度0.01 mm/s。试件安装后，试件与夹具、试验机机头与夹具之间存在配合间隙。微调试验机机头位置，使试件受一较小的初始拉力(小于100 N),此时各处配合间隙的接触关系均已经稳定，试验机荷载—位移呈现线性关系，安置好采集设备后即可正常加载。需要注意的是，加载过程中必须保证加载的对称性，不能出现偏心。

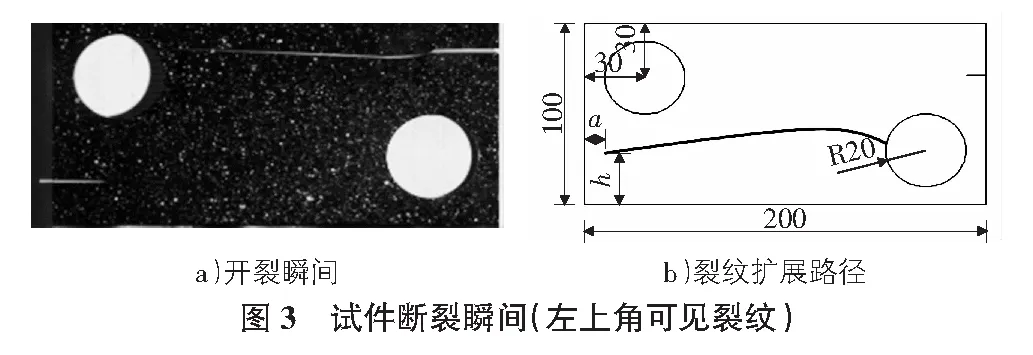
为观察试验过程，所有试件在实验前均喷涂了黑漆和白色散斑。以试件1-2为例，图3为试件1-2断裂时的情况。

3 试验结果

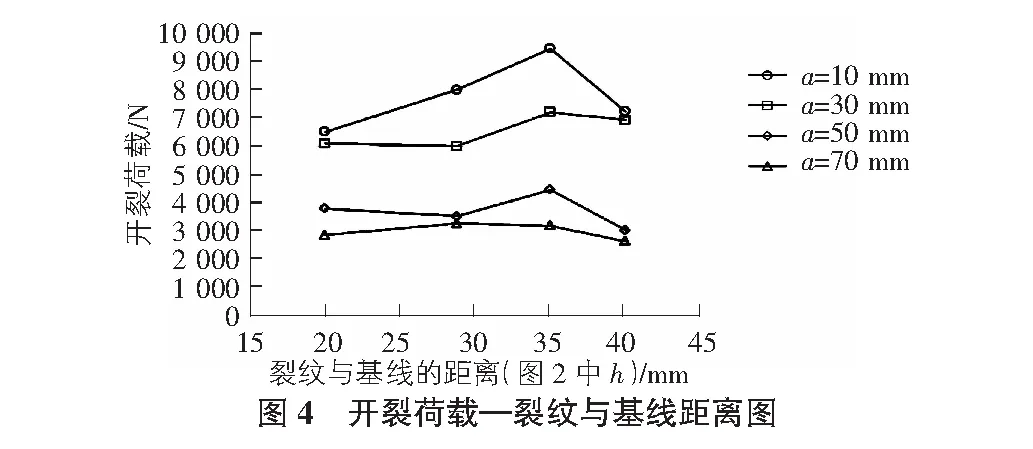
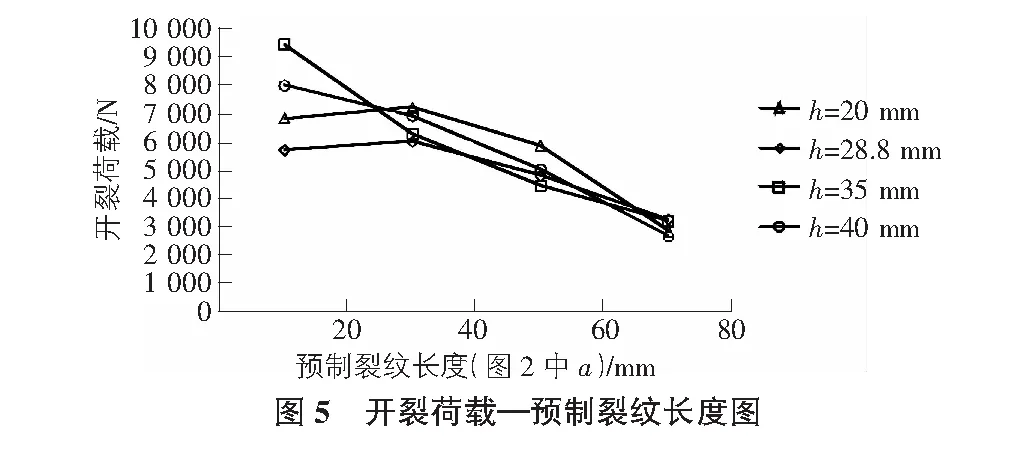
预制裂纹的位置和长度对有机玻璃板的开裂荷载存在显著影响，不同条件下试件的开裂荷载如图4，图5所示，预制裂纹与圆孔过近或过远都会使得试件的破坏荷载下降。当裂纹与圆孔位置适中时，裂纹尖端位于圆孔后的低应力区内，因此开裂荷载得以提升，裂纹尖端距离圆孔过近使裂纹与圆孔之间的部分因圆孔与裂纹部位的不协调变形而破坏，过远则无法进入圆孔后方的低应力区。无论裂纹与圆孔的位置为何值，试件的开裂荷载均随裂纹长度的增加而减小，以h=35 mm的试件为例，当裂纹长度由10 mm增加至70 mm时，开裂荷载由9 454 N减小至3 194 N，减少66%。且当裂纹长度较长时，因裂纹尖端已经超过了圆孔后方的低应力区，圆孔与裂纹的间距对试件的断裂影响很小。

4 试验过程的数值模拟

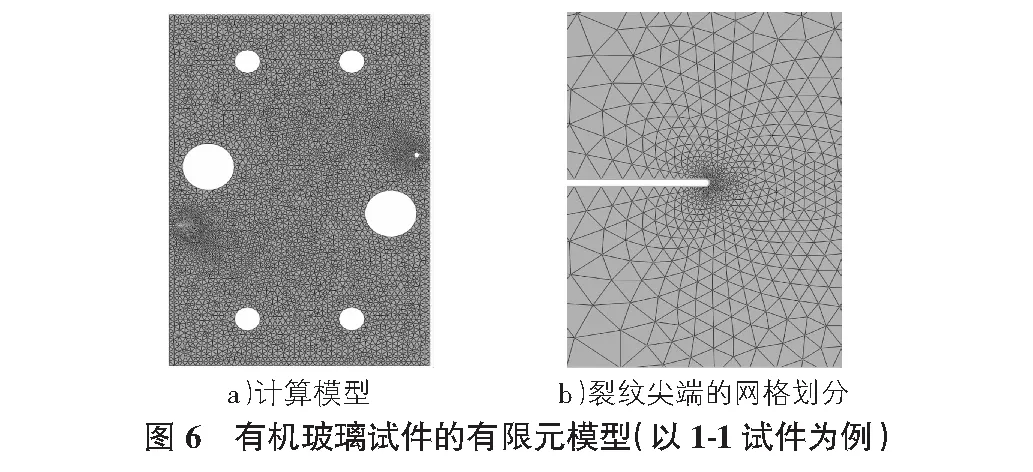
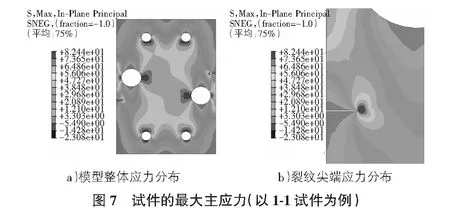
采用大型通用有限元软件ABAQUS建立试件的平面应力模型，在试件下端销孔处设置固定边界条件，在试件上端销处施加沿试件轴向的位移荷载，直至试件裂纹尖端达到最大应力。根据材性试验和相关文献，对有机玻璃材料，弹性模量取2 989 MPa,泊松比0.39，极限强度82.5 MPa。考虑到实际试件的两个裂纹完全一致，为减少计算量，本文仅以一个裂纹尖端为例进行研究，在另一裂纹尖端设置一圆孔以确保网格质量且减少计算工作量，最终使用的模型最大网格尺寸为4 mm，最小网格尺寸为0.06 mm，本文所用的计算模型如图6所示。采用上述有限元软模型进行计算，得到试件的应力分布规律，以1-1号试件为例，其破坏位移为1.95 mm(试验实测2.04 mm)，破坏荷载为6 892 N(试验实测6 840 N)，其计算结果是实测值的偏差均小于5%，最大应力点位于裂纹尖端处，最大应力84.22 MPa,计算结果如图7所示。从图7a)可以看出，圆孔上下方向均存在一个低应力区域，从图7b)可以看出，裂纹尖端的最大主应力分布呈蝴蝶形，符合断裂力学理论[7]。对各型试件进行计算，得到的结果均与试验结果相近。

5 结语

通过试验研究，确认了H.Azadi和A.R.Khoei采用流形元方法计算有机玻璃试件断裂过程所得结果的可靠性。也间接验证了其他断裂力学数值计算工具的可靠性。得出了有机玻璃试件中裂纹长度和裂纹与开孔距离与试件破坏荷载的关系。试验证明在网格划分得当的情况下，有限元方法也可以直接用于含有裂纹的脆性材料的断裂研究。