盾构机主驱动轴承的故障诊断方法

李贵红，姜小艳，杜 昕，李珊珊，王子恒

（兰州职业技术学院，甘肃 兰州 730070）

近年来，盾构机在地铁施工中应用越来越广泛，由于其集光、机、电、液、传感、信息技术于一体，设备复杂多样，体积庞大，维修不便，其安全性、可靠性成为厂家和施工方关注的焦点。随着盾构掘进地层工况的变化，大批盾构机主驱动轴承（回转支撑轴承、驱动小齿、轴端圆锥滚子轴承）在盾构掘进2～3km拆机转场时，需要对其解体检查，确保下个区间施工的设备保障。但是，此种检修往往造成维修不足、错误维修或过剩维修，增加了总体故障率。因此，国内外许多学者对其轴承故障诊断的方法进行了探索。杨宇［1］等提出了人工神经网络和EMD分解相结合的方法进行轴承故障诊断；Randall R B［2］通过循环平稳解调将机械系统中齿轮、轴承故障信号分离；Peng E K和张超等［3-4］分别将Hilbert-Huang变换与小波变换、EMD和奇异值差分谱理论相结合进行轴承故障诊断。但目前对于轴承系统中的复合故障研究较少。

文章提出了基于经验模态分解和冲击脉冲法的轴承故障诊断方法，通过实验验证，文中提出的方法在轴承故障诊断特别是在轴承复合故障诊断中能够准确的提取故障信号，有效识别并判别轴承等故障元件及损伤程度。

1 冲击脉冲法（SPM）

冲击脉冲法（Shock Pulse Method，SPM）是瑞典SPM Instrument AB公司提出的1套专门用于轴承故障检测的方法。

其原理是：当轴承存在点蚀、裂纹、疲劳等故障时，其滚动体经过缺陷位置时会引起冲击性振动，并产生高频冲击脉冲。这种冲击脉冲的强弱与轴承损伤程度成正比，该冲击脉冲被传感器接收，经处理显示冲击脉冲值，据此判断轴承状态，这就是冲击脉冲检测轴承故障的原理。冲击脉冲信号处理过程如图1所示。

图1 冲击脉冲信号处理过程

SPM法判断轴承工作状态时，需要建立判别标准。经过大量试验，采用标准分贝值dBn作为评判标准，并给出了经验公式，如式（1）所示

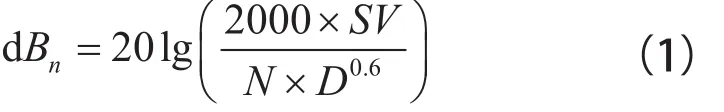
式中 N——轴承的转速，单位r/min；

D——轴承的内径，单位m；

VS—— 轴承故障产生的冲击脉冲值，单位ms-1。

标准分贝值dBn和轴承状态关系如表1所示。

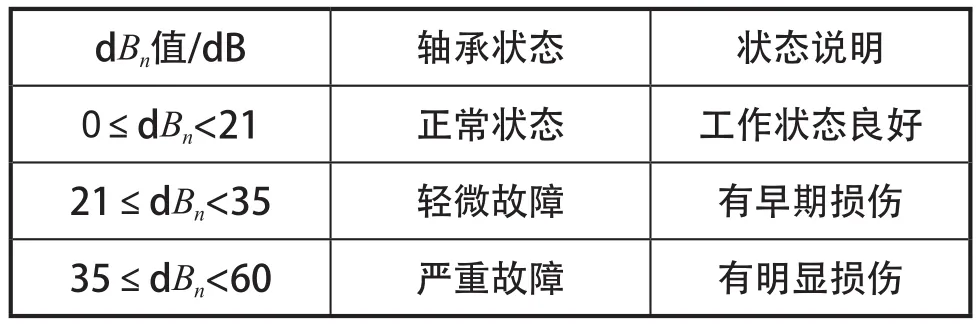
表1 标准分贝值dBn和轴承状态关系

采用SPM法，不足之处在于：

（1）只能判断轴承的总体状态，不能确定其中哪个元件损坏；

（2）当轴承系统中有多个轴承出现故障即有复合故障时，不同故障的特征频率相互叠加，直接采用SPM法检测可能产生误诊。

2 经验模态分解法（EMD）

经验模态分解（Empirical Mode Decomposition，EMD）是1种以傅里叶变换为基础的适用于非线性、非平稳信号且自适应的信号处理方法［5］，其关键是将一个复杂信号分解成若干个包含了原信号不同尺度和局部特征的IMF（Intrinsic Mode Function）分量，每个IMF分量应满足以下2个条件［6］：

（1）在所有数据段中，极值点与过零点的个数只能相等或相差1个；

（2）分别连接其局部极大值形成的上包络线和连接其局部极小值形成的下包络线的平均值在任一点处都为零，即上、下包络线相对时间轴局部对称。

对任一信号X（t）进行EMD方法分解步骤如下：

（1）找出信号中所有局部极值点，用3次样条线将所有局部极大值点连接拟合形成上包络线，用相同方法将所有局部极小值点连接拟合形成下包络线。

（2）将上、下包络线的平均值记为m1，求出

如果h1满足IMF的2个条件，则h1就是X（t）函数的第1个IMF分量。

（3）如果h1不满足IMF的条件，则把h1作为原始数据，重复步骤（i）和（ii），计算出上、下包络线平均值m11，再判断h11=h1-m11是否满足IMF条件。如果不满足，则重复循环K次，得到h1K=h1（K-1）-m1K，使h1K满足IMF的条件，记作C1=h1K，则C1为信号X（t）的第1个IMF分量。

（4）将C1从X（t）中分离出来，得到

将R1按照步骤（i）～（iii）重新处理，得到X（t）的第2个分量，记作C2，重复循环n次，得到信号X（t）的n个IMF分量，则有

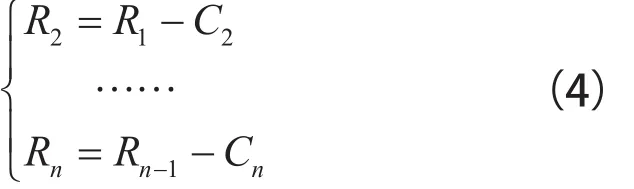
当Rn成为一个单调函数且不能再从中提取满足IMF条件的分量时，循环结束，这样就得到

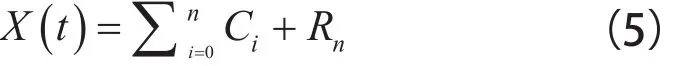
式中 Rn为残余分量。

由以上分析可知，任何1个信号X（t）都可以分解成n个IMF分量和1个残余函数之和，IMF的分量C1、C2、C3……Cn体现先高频后低频，由高及低，全面展现频率信号不同频段的成分，且每个频段所包含的频率成分是不相同的，会随信号X（t）的变化而变化。

图2为有复合故障轴承的原始振动加速度信号，该信号经EMD分解后得到8个IMF分量和1个残余分量，最后3个IMF分量及残余分量如图3所示。

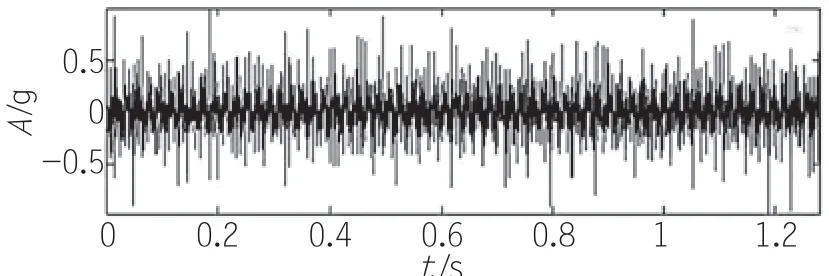
图2 故障轴承振动加速度信号

3 复合故障轴承信号处理实例

轴承故障实验装置如图4所示。实验中，分别在左边轴承外圈上、右边轴承内圈上通过线切割设置了典型局部故障，则整个轴承故障实验系统存在复合故障。实验中，将转速设置为1440r/min，实验装置中所用轴承为滚子轴承，其内径d为40mm，外径D为90mm，滚子个数Z为8个。

图4 轴承故障实验装置

右边轴承座处安装有振动加速度计，采集轴承振动信号，采样频率为15kHz，采样点数为16000，轴承振动信号如图2所示。对该信号直接进行包络解调，利用SPM法及式（1）计算相应的标准分贝值，结果如图5所示。其中上图为轴承振动信号，下图为包络谱换算的标准分贝值。由图可见：在内圈故障频率（122.11Hz）处，标准分贝值出现的峰值为18.4，但未超过21dB，根据SPM法该轴承运行状态正常，这明显与实际情况不符。

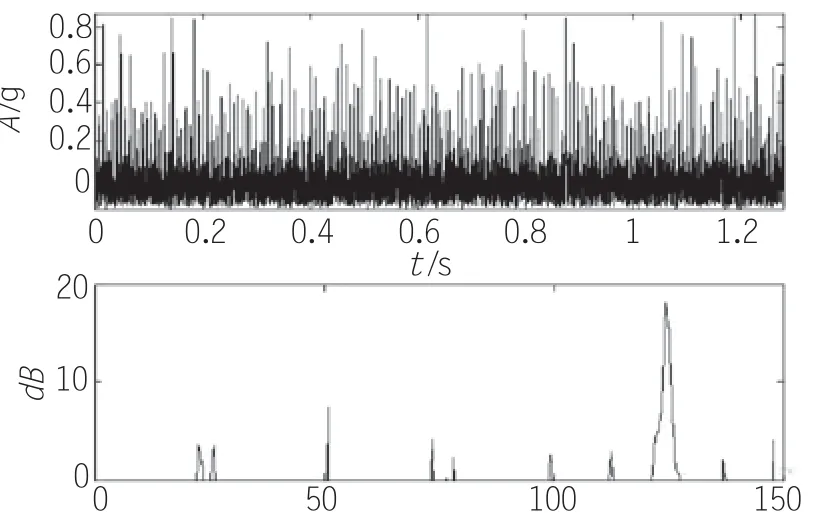
图5 直接包络解调分析结果

上述分析说明，SPM法判断轴承运行状态出现了误诊，其主要原因在于该轴承系统中，左右2个轴承分别存在外圈、内圈故障，2个故障产生的信号相互叠加在一起导致直接进行包络解调所得的包络谱幅值产生误差，进而导致故障诊断失败。

对图2所示的信号进行EMD分解，并对分解后得到的第1个IMF分量进行包络解调分析。结果如图6所示，内圈故障频率处出现了22.14dB的标准分贝值，根据SPM法判断该轴承存在内圈故障，与实际情况相符。

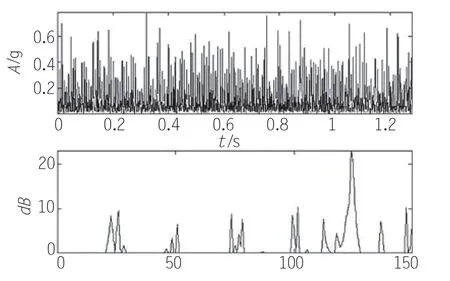
图6 第1个IMF分量包络解调分析结果

利用EMD分解处理左边轴承振动信号，并进行包络解调分析，同样得到了正确的诊断结果。不同的地方在于最大标准分贝值出现在第3个IMF分量的包络谱中，这说明轴承内外圈故障频率对应的载波频率处于不同频带。

以上实验说明，轴承系统存在复合故障时，轴承振动信号相当于2个或2个以上调制信号叠加，直接包络解调无法得到准确的诊断结果，只有通过基于EMD分解的包络解调分析，结合SPM法才能进行准确的诊断。

4 结束语

当整个轴承系统存在复合故障时，直接包络解调将出现较大的误差，从而导致故障诊断失败。因此本文研究了EMD分解和SPM法相结合的一种轴承故障诊断方法，并通过实验验证了该方法的有效性。实验结果表明，本文提出的方法可以有效的应用于轴承系统中的复合故障诊断。