CAPM模型在沪市的实证检验
2018-08-15周君
周 君
(首都经济贸易大学金融学院,北京 100070)
一、引言
20世纪60年代中期,Sharpe、Linter和Mossion提出了标准的资本资产定价模型-CAPM,该模型被广泛地应用于风险组合绩效评估及证券定价方面。经过近些年发展,中国的股票市场规模不断壮大,但在发行和交易方面存在许多问题。对于一个还不尽规范的市场,验证CAPM模型是否适用于市场还是很必要的。
二、文献综述
CAPM模型的内容为在市场均衡状态下,每种资产的预期收益率与其系统风险(用贝塔系数衡量)之间存在线性关系。在该模型提出后,学者们开始检验其有效性。利用美国34个共同基金1954年至1963年的年度数据,Sharpe发现基金的年平均收益率和贝塔系数呈线性相关。此后的二十余年,学者们利用实证检验纷纷支持该观点。80年代后,有学者提出质疑,认为股票收益率不仅仅受系统风险的影响。Banz(1981)提出“规模效应”,即小规模公司的股票收益率高于CAPM模型计算的收益率,也就是说股票收益率与公司规模负相关,且关系显著。
国内学者对CAPM在中国股市的适用性研究较为滞后,且多数学者持否定态度。杨朝军和邢靖(1998)提出CAPM并不适用于中国股票市场,系统风险并不是股票收益率的唯一度量,股本的规模以及流通股占总股的比例都影响股票收益率。国内学者结论的得出可能是因为数据选取的时间跨度小,样本量不足。有理由相信随着证券市场的不断完善,CAPM在中国的适用性检验会越来越明朗。
三、实证研究设计
(一)数据和样本
本文随机选取2015年至2017年沪市A股100支股票(ST股除外)的日收盘价进行检验,并借助Stata软件进行数据处理。数据来源于国泰安数据库。
(二)相关变量定义
市场投资组合的日收益率为上证A股指数的日收益率,包括沪市所有的上市A股,并以股本为权数。个股的日收益率为考虑现金红利再投资的日个股回报率,股票组合的日收益率为组合内个股日收益率的加权平均,权重为个股的流通市值平均值。无风险收益率采用日度化的1年期定期存款利率,经过计算可得该利率为0.012%。
(三)研究方法
本文采用时间序列检验和横截面检验。检验中用到的时间序列方程如下:
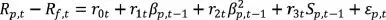
其中:Rp,t是组合p在t期的日收益率,Rf,t是t期的无风险收益率,βp,t-1为组合t-1期的贝塔系数,Sp,t-1为t-1期β与无关的解释变量,代表回归残差的标准差,εp,t是 t期的残差,r0t、r1t、r2t与r3t是待估计参数。
检验CAPM的适用性,就是对以下四点检验:第一,资产的风险与收益是否线性相关。如果r0t不显著,且其值不显著异于零,线性关系存在;第二,资产的风险与收益是否正相关。如果r1t显著,且估计值大于零,正相关关系存在。第三,贝塔系数是否是资产的风险的唯一度量。如果r3t不显著,且其值不显著异于零,则说明是唯一度量;第四,截距项是否为0。如r0t果不显著,且其值不显著异于零,则截距项为0。
在检验中,本文将三年分为三期。检验过程如下:首先利用第一期数据,将各股的日超额收益率与市场的收益率进行线性回归,估计个股的βi,再按βi大小降序排列,将100支股票分为十个组合。其次结合第二期数据,计算各组的日收益率,回归后得到各组的βp值,以及Sp。最后采用第三期数据,对以下四个模型进行回归分析:
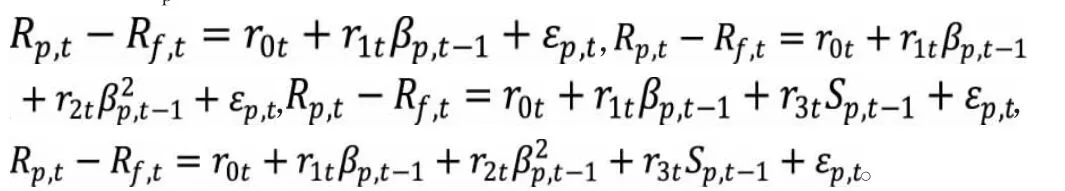
四、实证检验
对第一期数据进行回归后,得到β1=1.661...β100=0.515。排序后分为十组,进行回归得到其βp值以及Sp,结果如下:组合1的β1=1.3827,S1=0.0063;组合2的β2=1.3827,S2=0.0085…组合10的β10=0.917,S10=0.0105。最后结合第三期数据,先估计各组第三期平均日超额收益率,再利用第二期得到的βp和Sp值对上文四个模型进行回归分析,结果显示在5%的显著性水平下,4个模型中的参数均未通过显著性检验,且不显著异于零,各模型也并不显著。基于该结果,可认为CAPM并不适用于沪市。可能是因为个股和组合的β在第一期降序排列,但在二三期呈现无序的状态,也就是说个股以及组合的β系数不稳定。
五、结论
本文随机选取沪市A股100支股票2015至2017年的日收盘价数据进行实证检验,首先对个股的日超额收益率与市场收益率进行回归,得出个股的β值,分为10组后再回归,得到组合的β值与残差项的标准差。最后结合第三期数据对四个模型进行回归,得出CAPM并不适用于上海资本市场的结论。
