基于结构变化与共同因子串行效应的面板协整检验

陈海燕

(重庆工商大学 长江上游经济研究中心，重庆，400067)

一、引 言

Engle和Granger提出的协整方法已成为分析非平稳经济变量之间数量关系的最主要工具之一［1］。随着数据结构认识的不断加深，分析时间序列数据的协整理论扩展到面板数据，Kao、Pedroni等较早地提出了基于残差分析的面板协整检验方法，并假设数据截面之间是不相关的［2－3］。由于国际贸易、资本流动和技术溢出、劳力转移等多方面的相互影响，各个国家或地区的经济发展之间存在着千丝万缕的联系，导致面板数据截面个体之间存在着截面相关，Bai和 Ng、Bai和 Kao、Westerlund、Bai等研究了截面相关情形下的面板协整检验方法，并采用协整回归残差的共同因子结构来刻画数据的截面相关［4－7］。同时，由于强烈的外生冲击，比如体制变迁、经济转型、金融危机、技术革命等，都将造成经济数据发生结构性改变，Westerlund、Gutierrez等考虑了带结构变化的面板协整检验［8－9］。进一步地，Westerlund、王维国、Banerjee等研究了截面相关和结构变化共同影响下的面板协整检验［10-12］。

数据结构的复杂性影响着检验方法的发展。面板协整检验从截面独立到截面相关、从结构稳定到结构变化的演变正说明越来越多的学者关注着数据基本结构和模型的具体形式。面板协整检验中截面相关多以共同因子结构予以刻画，结构变化可以分为水平变化、斜率变化，或均值变化、方差变化等，处理方式一般是分别处理，将面板协整模型转换为截面独立或不存在结构变化的情形后再继续进行参数估计和假设检验。Westerlund和Edgerton研究了带趋势项的面板协整模型［10］，采用主成分分析估计出回归残差里的共同因子项，通过退因子使得模型残差满足截面独立的假设，再运用Bai和 Perron的方法［13］进行结构变化点估计，最后根据Westerlund和Edgerton［14］提出的方法针对含结构变化的模型提出协整检验统计量。王维国等进一步考虑了不带趋势项的面板协整模型，并采用与Westerlund和Edgerton［10］一样的方法处理模型［11］。Banerjee 和 C-i-Silvestre 研究的模型形式［12］与王维国等［11］类似，但是检验思路有差异，首先采用正交投影去掉结构变化，将模型转化为仅带共同因子的形式，再采用与 Bai和Ng［4］类似的主成分方法处理面板协整模型，最后提出协整检验统计量。而Bai、Westerlund等分别采取退因子和退结构变化处理面板数据模型［4，14］。

对带结构变化和共同因子的面板协整检验模型进行退因子和退结构变化处理是可行的，易将模型转换为已知形式，但是也容易忽略结构变化和共同因子的相互影响。Yamamoto和Tanaka研究了单变量面板数据共同因子载荷系数的结构变化情形，结果表明共同因子项发生结构变化将影响因子估计［15］。陈海燕通过外商直接投资与经济增长的面板协整模型证实共同因子项确实会发生结构变化，且改变着已有面板协整模型设定形式和实证分析结论［16］。实际上，在面板数据截面独立假设下，单个截面个体结构变化不受其他截面的影响，这与传统的单一时间序列结构变化类似，但当面板数据存在截面相关时，截面个体的结构变化会相互影响、相互作用，表现出共同变化趋势。此时，结构变化与共同因子并不是平行作用于面板数据模型中，而是形成相互连接的串行递进关系。

本文主要创新在于提出适宜结构变化与共同因子串行效应的面板协整检验，以补充面板协整检验理论，增强非平稳面板数据模型的实用性。

二、串行效应分析

(一)定义与影响

带结构变化和共同因子的面板数据模型一般设为:

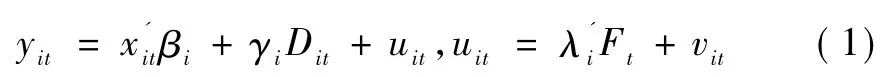
借鉴通信信号里的信息结构，模型(1)中的影响效应可以定义为并行(parallel)形式，加入或去除某一种效应并不会改变另一种效应的存在，比如Baltagi等考虑的异方差和序列相关影响［17］，Breitung分析的序列相关和固定效应影响等［18］。信息结构还有一种形式为串行(serial)，主要表现为多种效应的串联、递进关系，某一种效应制约着另一种效应的存在。模型(1)为带结构变化和共同因子并行效应的面板数据模型，其原假设分别代表了联合和条件并行情形，那么串行效应下的面板数据模型①此处仅是为了对应模型(1)，直观地给出了模型(2)的形式，串行效应面板协整模型具体形式见下一部分内容。结构变化有可能发生于共同因子或载荷系数。为:

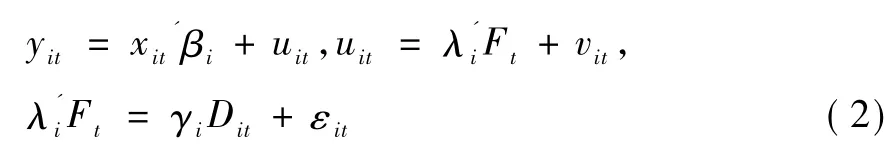
当λi≠0成立时，模型(1)存在共同因子;当λi≠0，γi≠0成立时，共同因子项发生结构变化。λi=0成立意味着γi=0，这与 H0a不同，且不存在并行结构下的原假设当∶γi=成立时说明模型的共同因子项没有发生结构变化。

将串行效应按照并行效应进行处理，将导致模型不可用。假设数据之间存在共同因子项发生结构变化的串行效应，则有:

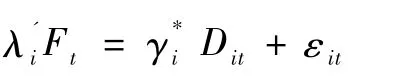
可以写成:

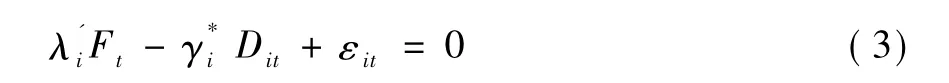
若按照并行效应模型(1)进行处理，设:

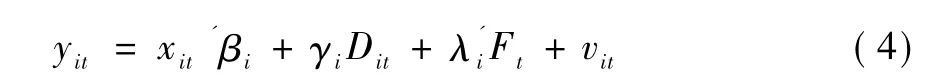
此时，对于变量 { yit}，共同因子 Ft和结构变化Dit均可以看成自变量，γi和 λi为待估系数，则式(3)表明模型(4)中自变量存在近似共线性。从违背经典假设的计量经济学理论可知，近似共线性将导致参数估计量非有效、经济含义不合理等后果。这说明，忽略串行效应而采用并行效应的方式处理结构变化与共同因子，会导致近似共线性的情况发生，致使参数估计无效、模型解释不合理。

(二)存在性检验

为了区分结构变化与共同因子的并行效应和串行效应，在模型(1)和模型(2)的基础上提出一般性的单变量面板数据串行效应模型:

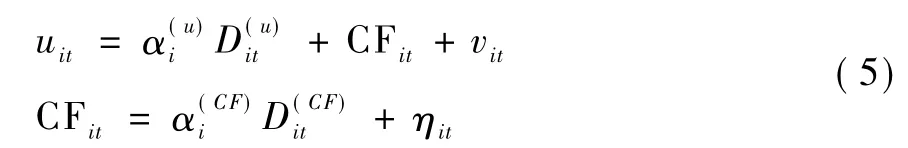
其中，vit和ηit表示随机扰动项。CFit表示截面之间的共同因子项，一般文献中记为表示序列uit的结构变化表示共同因子的结构变化和α(i

CF)分别为结构变化系数。

为了进一步讨论串行效应的检验思路，设置两个假设，分别为:

串行效应存在性检验的步骤如下:

1．采用CD统计量对序列 uit进行截面相关检验［19］，其中

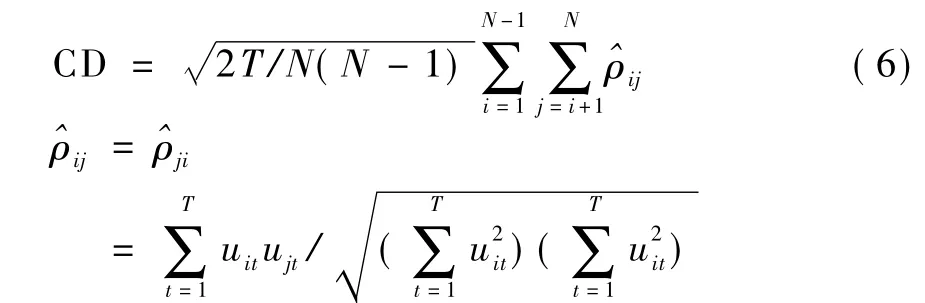
2．采用主成分方法对存在截面相关的数据uit进行共同因子分解。将共同因子项记为CFit，退因子后的序列记为。

3．采用Bai中提出的SSR检验统计量分别对序列uit、共同因子项CFit、退因子序列进行同质结构变化检验［20］。均值结构变化的检验统计量为:

4．根据式(3)中的结构变化检验结果，按照不同的假设给出判断。若序列uit不存在结构变化，接受假设;若退因子序列不存在结构变化，而共同因子CFit存在结构变化，拒绝假设;若退因子序列存在结构变化，而共同因子CF不存在结构变化，it接受假设;若退因子序存在结构变化，而共同因子CFit存在结构变化，拒绝假设。

三、面板协整模型设定与估计

带并行效应的面板协整模型可以解释经济变量存在截面相关和结构变化时的数量关系，处理方式一般是将模型转换为截面独立、结构稳定的形式再提出检验统计量［10－12］。并行效应模型里结构变化与共同因子是分别考虑的，结构变化代表的是刨除截面相关影响之后的数据信息。串行效应模型里共同因子不再是稳定的，而是发生了结构变化。有研究认为共同因子可以代表经济基本面［21］，串行效应认为驱动研究变量的基本面发生了结构变化。

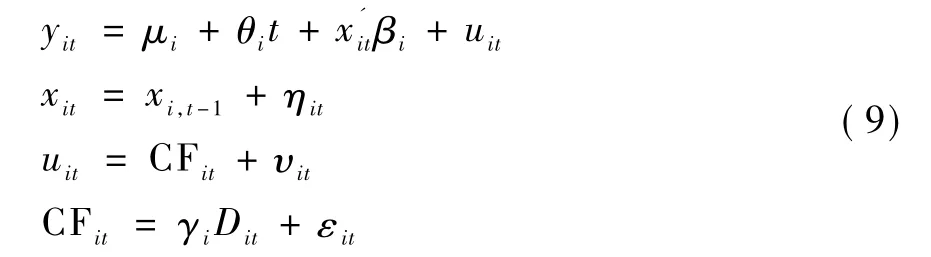
其中，xit和yit为被检验变量，μi为共同常数项，CFit为共同因子项，Dit为结构变化项。uit为协整回归扰动项，其平稳性决定了变量xit和yit是否存在协整关系。υit为 uit中去除共同因子影响之后的剩余扰动项，εit为共同因子项中去除结构变化之后的剩余扰动项。一般地，记 CFit=Ft。Ft表示各截面在时间上的共同因子，λi为因子权重，λi和Ft可以通过主成分分析得到。

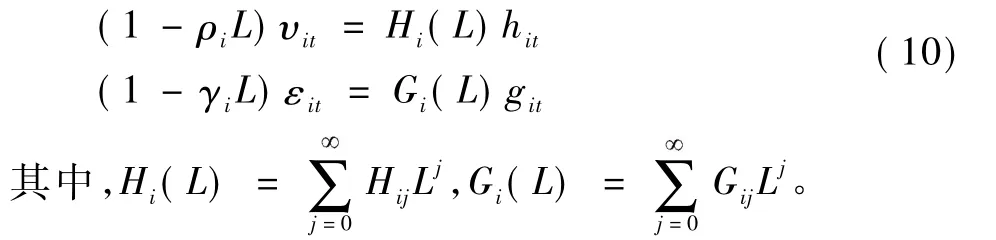
模型(9)的原假设H0:不存在协整关系，备择假设为存在协整关系。

假设1:对于非随机的系数 λi，有 ‖λi‖ ≤ M，‖A‖ =trace(A'A)1/2，M为小于无穷大的正数。对于随机的系数 λi，有 E‖λi‖4≤ M。

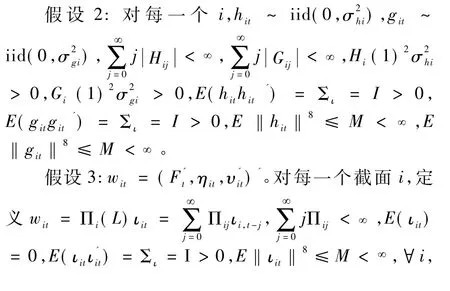
假设 4:ηit、hit、git之间互不相关。

假设5:ηit、υit为截面独立的随机扰动项。

假设1保证因子载荷是可识别的。假设2允许变量存在较弱的序列自相关。假设3可以得到wit的方差估计。假设4限制了变量之间的相关性，认为这些扰动项都与xit不相关。假设5保证变量xit不存在影响共同因子项的因子信息，保证共同因子项代表了uit中的截面相关信息。在串行效应成立的前提下，假设6说明uit的平稳性与变量υit一致，由系数ρi决定。

模型(9)的扰动项不满足经典假设，系数βi的最小二乘估计量非一致，对模型(9)取差分将使得原假设成立的条件下Δuit为平稳序列，可以得到系数的渐近一致估计量。有:

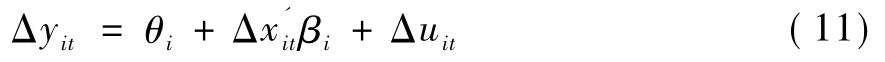
王维国等、Banerjee和C-i-Silvestre均研究的是异质结构变化［11－12］，并行效应下式(1)中的共同因子项包含或覆盖了截面个体趋同的所有影响，结构变化项不再存在截面相关，考虑为异质结构变化是适宜的。串行效应下模型(9)中的结构变化发生于共同因子项，应考虑为同质结构变化，表示影响截面个体的基本面发生了结构变化。这里仅考虑了共同因子Ft的结构变化，系数λi也可能发生结构变化［23］。

四、面板协整检验

(一)构造检验统计量

模型(9)可以写为:两边取差分，有:

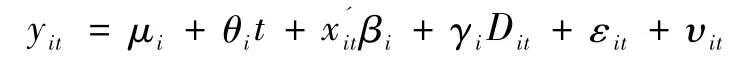
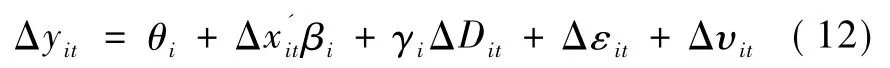
因方程(9)里含有趋势项θit，对差分后的序列去均值，即可消除趋势项，得:

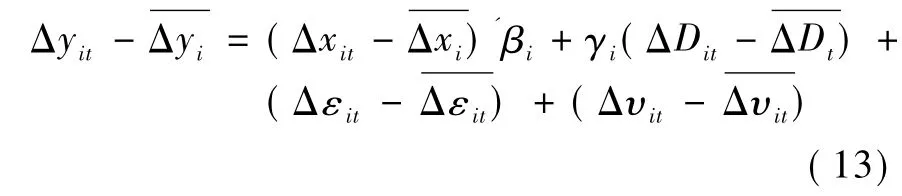
共同因子项分解为结构变化项和扰动项，εit可能存在截面相关，且是与共同因子Ft相关，设:

此时ξit与uit同阶，对uit进行平稳性检验等价于对ξit进行平稳性检验。

在对模型进行变换以后得到不存在截面相关和结构变化的变量ξit，协整检验式为:

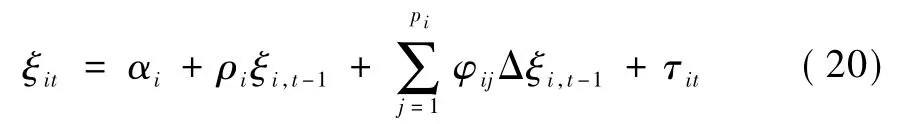
检验统计量为:

其中，tiT为个体ADF检验统计量，极限分布为正态分布。

(二)协整检验步骤

存在串行效应时面板协整检验步骤为:

1．采用串行效应存在性检验确定模型是串行效应还是并行效应。

2．若模型带趋势项，先进行差分再去均值得到模型(12)，如果模型不带趋势项，直接差分即可。

4．根据式(19)求出检验统计序列ξit。

5．根据式(21)求出序列ξit的单位根检验统计量，并进行模型协整关系判断。

若ξit～I(1)，则接受原假设，认为变量xit和yit之间不存在协整关系，反之则认为存在串行式协整关系。

五、实证研究

并行效应下面板数据模型是将结构变化和共同因子分别进行处理，具体表现为刨除共同因子影响后的数据发生了结构变化。串行效应研究发现，分别处理结构变化和共同因子将忽略二者之间的递进关系，因为共同因子也可能发生结构变化。外商直接投资与经济增长之间的影响关系历来受到研究者们的关注，面板数据模型是常用分析工具之一，但是已有研究较少考虑面板数据模型的结构变化和截面相关［24］。

下面采用中国30个省区(西藏除外)1995—2016年的国内生产总值GDP为被解释变量，外商直接投资FDI为解释变量，分析其基本结构和影响关系，以说明在实证研究中面板数据串行效应的存在性。考虑到物价和计量单位的影响，在计算时采用变量的对数形式。将表示经济增长的序列记为y。以下所有计算结果和图形由R语言运行而得。图1给出了序列y的原始数据和按式(18)处理后的序列y*对比图，可以发现序列y*中的趋势性被减弱，序列y增长幅度越大，序列y*的波动性就会越大。

图2给出了共同因子趋势图，发现共同因子从第14个时间点即2008年开始发生波动性变化。共同因子是面板数据截面相关的主要表现形式，代表的是驱动每个截面个体的共同因素或共同推动力，也可以解释为总体经济基本面［21］。各省市的经济增长和FDI受到了来自中国总体经济发展水平、对外贸易战略等的共同影响，该共同影响在2008年因国际环境的改变发生了结构变化。若按照并行效应模型(1)对数据进行处理，去除共同因子的影响，对残差序列vit按照式(8)进行结构变化检验，发现并不存在均值或方差结构变化［16］。这说明忽略共同因子和结构变化的串行效应将导致实证分析结果与经济变量实际关系发生偏离。

根据式(15)可知，均值变化变量差分以后每一个体中仅有一个年份值为1，其余全为0，这将导致投影矩阵数值过小，很难完成系数估计，所以无法对均值变化的情形进行检验。图3给出了模型发生方差变化时式(18)中系数φi的估计值，表示不同省市受到共同因子的影响大小，其最小五个值对应的省份分别是青海、甘肃、海南、宁夏和新疆，最大三个值对应的省份分别是广东、江苏和山东。图4给出了式(15)中方差变化 σi的估计值，说明不同省市之间的结构变化程度不同，受结构变化影响最大的省市分别是广东、山东和北京。图3和图4的分析结论与中国吸引外资较多的省份更易受到国际环境改变的冲击现实吻合。

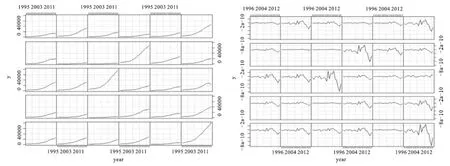
图1 y原始序列和处理后的序列y*对比① 对文中原始数据和R程序有兴趣的读者请和作者联系。

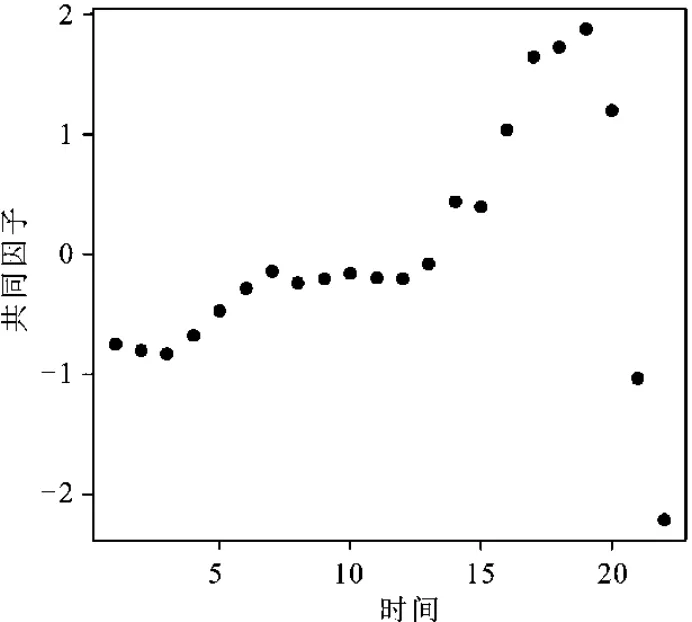
图2 共同因子图

表1给出了式(19)中统计量的单位根检验结果，在显著性水平为0．05时应拒绝原假设，序列 ξit没有单位根，认为变量之间存在长期均衡关系。诸多研究均表明经济增长与FDI之间存在长期均衡关系，此研究结论与已有研究结论一致，但是串行效应面板协整检验更有力地证实了驱动经济增长与FDI的共同因子在2008年发生结构变化。

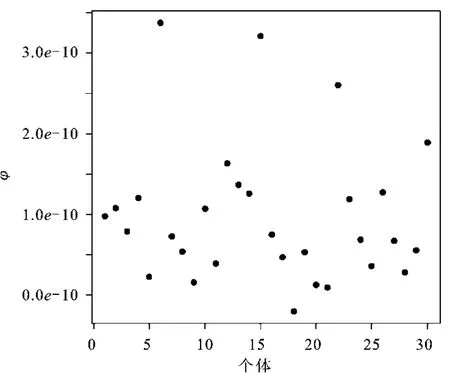
图3 系数 φi估计值图

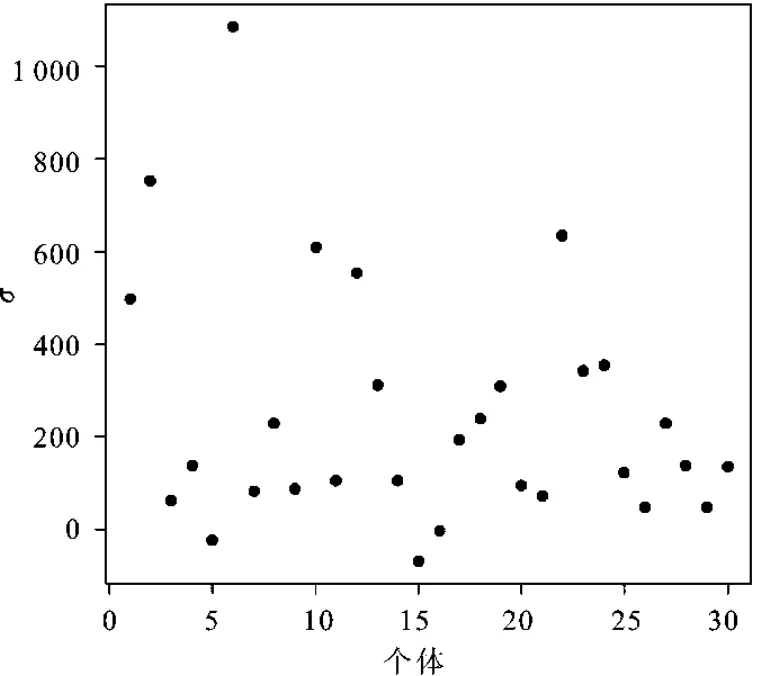
图4 系数σi的估计值图

表1 序列 ξit的单位根检验表

按照并行效应的分析方法，刨除共同因子影响之后中国经济增长与FDI之间的长期均衡发展关系并没有发生结构变化，这与2005－2016年间全国进行的经济结构调整并不符合。特别是在2007—2008年因美国次贷危机影响，中国各省市面临的对外贸易国际环境发生了较大改变，全国采取了一系列举措以保持经济健康稳定发展，因此代表全国经济结构调整和贸易战略改变的共同因子在2008年确实发生了结构变化。说明在经济增长与FDI长期均衡关系分析中，忽略共同因子与结构变化的串行效应将导致实证分析结果出现偏误。

六、结 论

本文对带结构变化和共同因子的面板数据影响效应进行了界定，率先提出了串行效应和并行效应，同时给出串行效应的存在性检验方法，进而提出串行效应协整检验理论，并从模型设定、参数估计、假设检验、极限性质等方面完善了该检验理论。最后，应用中国实际经济数据证实了共同因子发生结构变化的串行效应模型更符合中国经济增长与FDI的长期均衡关系，说明了区分面板数据内在效应存在方式的重要性。

虽然串行和并行式效应下存在相似的协整方程表现形式，使得面板协整检验结果不会出现较大差异。但是，对实证研究结果的影响却是巨大的，这改变着经济关系分析时变量的共同因子与结构变化相互作用的内在逻辑，关系着变量数据结构真实信息的解析。因此，非平稳面板数据建模过程中要区分结构变化的来源，注重影响效应的存在方式，否则将导致传统结构变化处理方法失效，经济分析脱离现实、失去意义。