基于自适应算法的谐波检测方法研究
2018-08-14彭咏龙张坤锋李亚斌杨朋凯黄江浩
彭咏龙,张坤锋,李亚斌,杨朋凯,黄江浩
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引 言
随着电力系统的电力电子化,产生的谐波问题日益严重,严重影响到电力系统的稳定运行。解决电力电子设备产生的谐波问题一般有两个思路:一是对电力电子设备的自身结构进行改进,使其尽量少的产生谐波;二是增加谐波抑制设备,比如有源滤波器等,对产生的谐波进行补偿。
谐波检测的精度和速度是有源滤波器问题的研究重要方向之一[1]。由于低通滤波器的影响,传统的ip-iq谐波检测算法存在响应速度慢和检测精度较差的问题。文献[2-3]采用一种变步长的LMS算法替代低通滤波器的影响,当变化速度较快时采用较大步长,反之则采用较小步长。但其动态响应效果仍较慢。文献[4-5]采用快速傅里叶变换的方法来进行谐波检测,该方法数据处理量较大,计算复杂,不仅响应速度慢,而且工程应用型较差。文献[6]采用模糊控制的方法进行谐波检测,其精度具有较大的优势,但运算过程的复杂性对硬件的处理性能要求很高。
在此基础上,提出了一种基于改进型的变步长LMS/LMF算法的自适应滤波器取代低通滤波器的作用,并对其进行公式推导。通过仿真验证验证了提出的算法可靠有效。
1 传统型谐波检测算法
三相瞬时无功理论是在20世纪90年代由日本的赤木泰文提出来的, 在此基础上提出的谐波检测算法极大的促进了有源滤波器的推广和发展[7]。其原理如图1所示。
三相电流ia、ib、ic经过C32变换,变换到矢量坐标系下的iɑ、iβ:
(1)
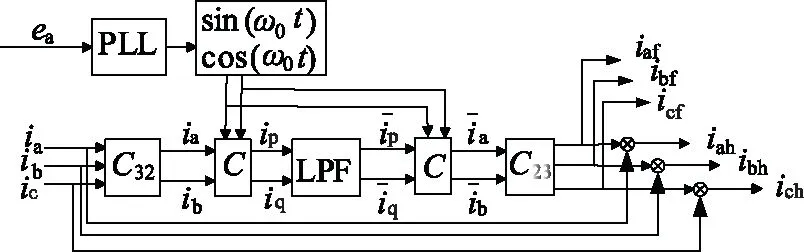
图1 基于瞬时无功理论的谐波检测算法Fig.1 Harmonic detection algorithm based on instantaneous reactive power theory
再经过C变换,得到三相瞬时无功电流iq和三相瞬时有功电流ip:
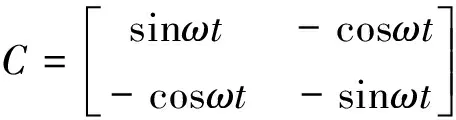
(2)
此时三相瞬时无功电流iq和有功电流ip中包含直流和交流分量。低通滤波器滤去其交流分量,就可以得到三相瞬时无功电流iq和有功电流ip的直流分量,经过C、C23变换,最后可以得到三相电流的ia、ib、ic的基波分量iaf、ibf、icf:
(3)
上述即为基于瞬时无功理论的ip-iq算法的谐波检测原理[8],传统的ip-iq谐波检测算法受低通滤波环节的影响,导致谐波检测的起到速度较慢,同时当负载变化时不能很好的跟踪负载电流的变化,导致谐波的检测不够准确,对有源电力滤波器的精度和速度影响较大。
2改进型谐波检测算法
自适应滤波器的原理如图2所示。图中i(n)为输入电流分量,e(n)为误差信号,xk(n)为参考输入信号,wk(n)为权值系数,y(n)为输出信号,权值因子的调整采用固定步长的LMS算法[9]。在上述传统LMS算法基础上,通过变步长LMS/LMF算法,用于调整权值系数,使自适应滤波器的检测精度和速度有了明显的提高。
算法遵循的基本原则为:当自适应滤波器输入的原始信号发生突变时,整个系统主要采用LMF算法,同时采用较大步长调整权值系数,具有较好的动态响应速度。当整个系统的输入信号趋向稳定时,整个系统采用LMS算法,同时采用较小的步长因子调整权值系数,具有较好的检测精度。因此设算法调整函数为:
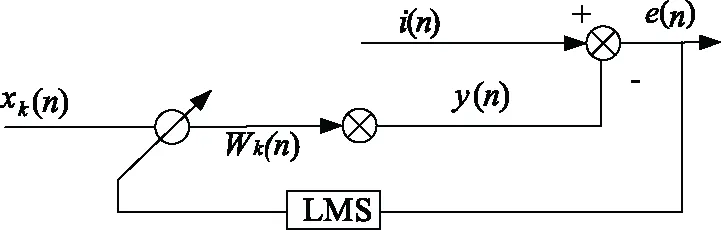
图2 基于LMS算法的自适应滤波器的基本原理图Fig.2 Basic principle diagram of adaptive filter based on LMS algorithm
(4)
由此可知,当rn=1时整个系统采用LMF算法,当rn=0时整个系统采用LMS算法。梯度更新权值系数wk(n),则:
(5)
en=i(n)-wk(n)xk(n)
(6)
则将上述公式(4)~公式(6)代入,可得权值更新的公式为:
(7)
对步长因子的调整采用双曲正切函数的方法:
(8)
p(n)=rp(n-1)+(1-r)e(n)e(n-1)
(9)
β(n+1)=ξβ(n)+ηp2(n)
(10)
双曲正切函数底部波形变化较快,使误差信号在接近于零时变化较大,引入系数m改善函数底部波形,也使误差信号在接近于零时变化显得更加平缓。β用来控制函数的变化范围。
采用归一化方法和记忆因子的方法对调整因子rn进行更新,则:
rn+1=arn+a2pn2
(11)
(12)
式中的a1、a2、β、k均为记忆因子,表示过去的误差和电流对现在的影响程度,以实现LMS和LMF的份额的调整。以上公式(3)~公式(12)便构成了新型的LMS/LMF算法。为了算法的稳定性,u(n)和rn的值需要对其进行限制[10]:
(13)
(14)
3 仿真验证
为了验证上述算法的性能,通过建立仿真模型对其进行验证。在MATLAB的Simulink模块建立模型,其中采用三相桥式不可控整流电路作为负载。传统低通滤波器采用2阶巴特沃斯滤波器,阶数过大收敛速度较慢,而阶数过小时,其低通滤波器的性能也会降低。因此传统的有源滤波器经常采用二阶的巴特沃斯低通滤波器,较好的平衡了两者之间的平衡。当负载未突变时,图3为基于传统的ip-iq算法的谐波电流检测结果,受到低通滤波器的影响,其检测速度较慢,需要将近1.5个周期才能趋向稳定。
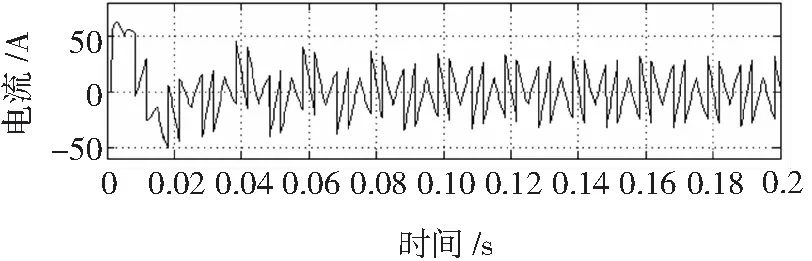
图3 非突变负载下传统的ip-iq算法的谐波检测结果Fig.3 Simulation constant load harmonic current result of the harmonic current detection method based on the ip-iq algorithm
图4为基于改进型的ip-iq算法的谐波电流检测结果,采用基于变步长LMS/LMF算法的自适应滤波器,其检测速度有明显的提高,仅需要0.5个周期就能趋向稳定。
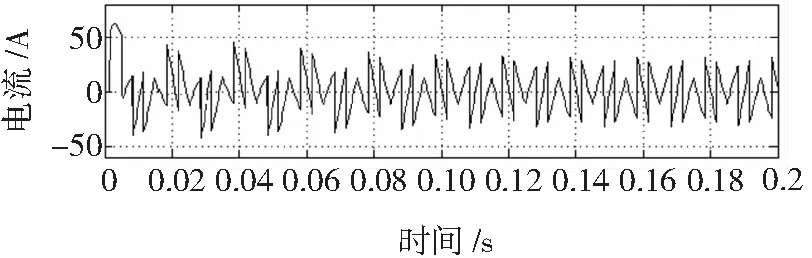
图4 非突变负载下改进型ip-iq算法的谐波检测结果Fig.4 Simulation constant load harmonic current result of the harmonic current detection method based on the improved ip-iq algorithm
当负载发生突变时,图5采用传统的ip-iq算法的谐波检测结果,其谐波检测的速度较慢,当负载发生突变时,并不能迅速跟上系统负载的变化。
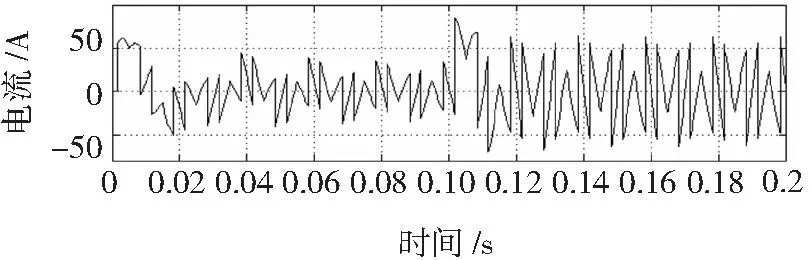
图5 突变负载下传统的ip-iq算法的谐波检测结果Fig.5 Simulation mutated load harmonic current result of the harmonic current detection method based on the ip-iq algorithm
图6为采用改进型ip-iq算法的谐波检测效果,谐波检测速度有了明显的提高,当负载发生突变时,其跟踪速度有了明显的提高。
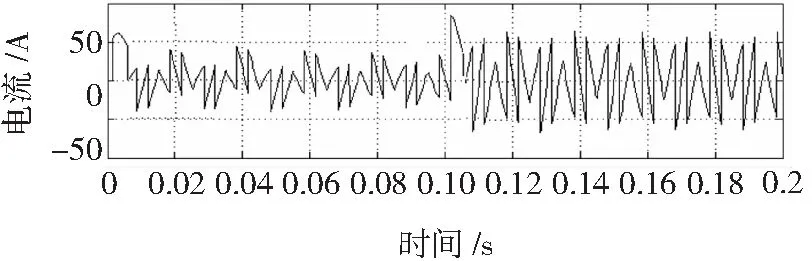
图6 突变负载下改进型ip-iq算法的谐波检测结果Fig.6 Simulation mutated load harmonic current result of the harmonic current detection method based on the improved ip-iq algorithm
4 结束语
由于低通滤波器的影响,传统的ip-iq谐波检测速度和检测精度都较差。提出了一种改进型的谐波检测算法,采用了一种基于变步长LMS/LMF算法的自适应滤波器,替代了传统的低通滤波器滤去交流分量的作用。在此基础上对其进行了仿真验证,仿真结果表明,提出的算法可靠、有效,可以有效的解决传统ip-iq算法的响应速度和检测精度的问题,具有一定的工程应用价值。
