速度锁定装置对斜拉桥制动附加力的影响分析

2018-08-14朱金波周远智

交通科技 2018年4期

朱金波周远智

(贵州省交通规划勘察设计研究院股份有限公司贵阳 550081)

国内外学者对简支梁及连续梁等常规桥梁的梁轨相互作用做了大量的研究[1-2]，对斜拉桥的梁轨相互作用研究较少。而实际上，我国城市轨道交通已经修建了大量的斜拉桥，由于斜拉桥跨度较大，所以其钢轨制动附加力也更大。目前，计算钢轨制动附加力大多采用传统的干线铁路梁轨相互作用计算模型(即桥梁+两端一定长度的路基)，该传统模型不能较好地反映城市轨道交通高架桥的实际结构受力形式，本文采用考虑邻跨简支梁影响的有限元计算模型，该模型与实际轨道交通高架桥的结构形式更为相近。

1 计算模型

1.1 扣件阻力模型

选用《铁路无缝线路设计规范》[3-4]中的非线性扣件纵向阻力模型，该计算模型见图1。

图1 扣件纵向阻力计算模型

1.2 速度锁定装置简化模型

速度锁定装置(LUD)在静力条件下不会改变桥梁结构的原有功能，而在制动力作用下，又提供锁定功能，使得与该装置相连的构件共同承担制动力。设计人员要事先设定一个速度开关V0，当V>V0时，可用一个刚臂单元来模拟速度锁定装置。

1.3 列车制动力参数

本文模型中制动荷载是近似按照均布荷载加载于钢轨顶面来计算的，只按静荷载考虑，也未考虑列车制动过程中作用于轨面荷载的大小随时间的变化，但这种近似的模拟能充分反应荷载传递对梁轨相互作用的影响。

列车最大制动力主要取决于列车荷载及制动力率，而且最大制动力与制动前速度关系不大。轨面制动力试验结果证实了轨面制动力率与桥型、支座和线路条件无关，而与列车制动加速度有直接关系，在我国高速铁路中推荐高速铁路制动力率采用0.164，城市轨道交通桥梁由于车辆编组长度较短(6～8辆)，加上采用电气指令式传递制动信息,所以制动力率取值比铁路桥梁高,本文轨面制动力率取0.25。

采用地铁A型车的竖向荷载，则其计算的单线轨面制动力为28.07 kN/m×0.25=7.017 5 kN/m。本文在计算制动附加力时，采用单线制动考虑。

1.4 梁轨相互作用模型

本文采用7跨简支梁(跨径L=30 m)+斜拉桥+7跨简支梁(跨径L=30 m)模型计算轨道交通斜拉桥制动附加力，模型示意见图2。使用大型有限元软件ANSYS建立全桥模型，钢轨扣件纵向间距为1 m。全桥构件采用梁单元模拟，用非线弹簧单元模拟钢轨和主梁之间的扣件连接，主梁的高度用刚臂单元模拟。全桥模型的节点共计2 346个，梁单元共计2 299个,线性弹簧单元共计19个,扣件非线性弹簧单元共计720个。ANSYS软件建立的计算模型见图3。

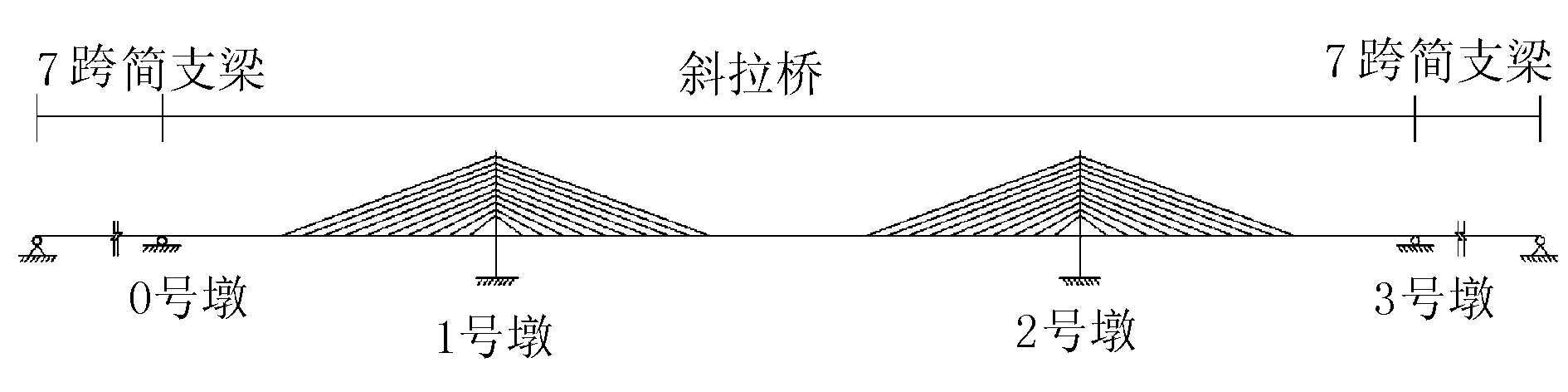
图2 全桥有限元模型示意图

图3 ANSYS计算模型局部

2 工程背景

以上海轨道交通16号线上的大治河大桥为研究对象，该桥跨径布置为80 m+140 m+80 m，共300 m，为两塔三跨单索面斜拉桥，采用塔墩梁固结体系。主梁采用预应力混凝土结构，截面形式为单箱双室斜腹板箱梁，主梁根部梁高5.6 m，跨中梁高3.6 m；主塔两侧各37.75 m范围内梁底曲线按圆弧线逐渐变化，其余部分主梁为等高度梁；主梁顶板宽为13.641 m、厚度为25 cm，根部底板宽度为7.60 m、厚度为80 cm,跨中底板宽度为5.71 m、厚度为30 cm；中腹板厚度为50 cm，两侧斜腹板厚从根部至跨中，由50 cm逐渐变为30 cm。

斜拉桥主桥箱梁采用C60混凝土。全桥共设置2×20对拉索，拉索纵向间距5.0 m，每对斜拉索为2根，横向间距1.3 m。斜拉桥主塔采用标号为C50的混凝土，主塔高20.5 m，横向宽2.5 m，主塔纵向宽从底部的5.4 m逐渐变化至顶部的6.5 m。

3 计算结果分析

本文设计了4种不同速度锁定装置LUD的布置方案。方案1：各桥墩均不设置LUD;方案2：仅在右侧主塔设置LUD;方案3：仅在两侧边墩设置LUD;方案4：在右侧主塔和两侧边墩设置LUD。不同速度锁定装置LUD布置方案的制动附加力见图4(其中横轴坐标0点为斜拉桥0号墩位置)。

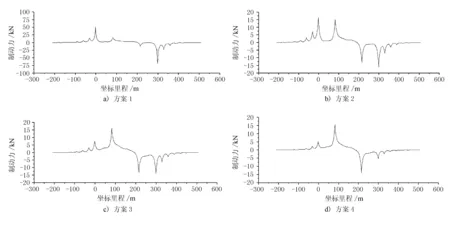
图4 钢轨的制动附加力

综合4个方案下制动附加力的最大(小)值，见表1。表2为传至各桥墩的制动反力。

表1 不同方案单轨纵向制动力

表2 各桥墩制动反力

由图4、表1和表2可见，不设置LUD的制动力最大值发生在斜拉桥的两端，而设置LUD后制动力的最大值均发生在列车荷载加载的起终点；设置LUD可有效地降低制动附加力，方案1的制动力最大为68.5 kN，方案2的制动力最大为15.8 kN，方案3的制动力最大为16.0 kN，方案4的制动力最大为15.2 kN；制动力由制动墩与设置了LUD的各桥墩近似平均分配，且制动力随着LUD数量的增多成比例减少。所以合理设置LUD能有效减小制动墩的制动反力。