看“视力”

梅颖

上海新虹桥国际医学园区美视美景眼科中心业务院长，副主任医师。天津医科大学早稻田眼镜职业培训学校名誉校长。国际角膜塑形学会资深会员（FIAO）、国际角膜塑形学会亚洲分会资深(SIAOA)会员、美国视觉训练和发展学会（COVD）会员。眼视光英才计划“明日之星”成员。《中国眼镜科技杂志》专栏作者。《中职教接触镜验配技术》副主编，《斜弱视和双眼视处理技术》编者。专著《硬性角膜接触镜验配案例图解》《硬性角膜接触镜验配跟我学》《视光医生门诊笔记》《硬性角膜接触镜验配跟我学 第2版》。

小学的语文课本中曾写道，中国长城是在太空中可以用肉眼看到的人类建筑，这是中国人一直都引以为豪的。2003年，当我国自主研制的“神舟”五号载人飞船发射成功，将中国第一名航天员成功送上太空，杨利伟在落地之后接受白岩松的现场采访，白岩松的第一个问题就是：您在太空中看到我国的长城了吗？杨利伟果断地回答：“没有看到！我们几个航天员，在绕地球飞行的14圈中仔仔细细地看，但谁也没找到长城。”因此，2004年小学语文四年级上册《长城砖》的课文被人民教育出版社删除了。难道真的从太空中无法看到长城吗？

1 如何定义1.0的视力

视力，亦称“视锐度”，就是外界物体两端在眼内结点处的夹角的倒数。视角的大小随物体的大小和与眼的距离而改变，并决定着物体在视网膜上成像的大小。人眼能分辨的物体成像的视角越小，表示视力越好。

要分辨两个相距很近的物体，必须在两个受刺激的锥体细胞之间至少有一个静止的细胞，才可将两个刺激点区分开，所以视力检查的最终目的是测定可以辨别的最小视角。现测得锥体细胞的直径约为5μm，以此计算在眼球结点处的夹角是1’，所以人眼以1’视角为最小视角，对应小数视力1.0。

有关视力（视锐度）的定义，视光学教材《视光学理论和方法》一书中有详细描述，如图1：

图1

2 看长城

下面来计算一下，如果按正视眼最小分辨视角是1’来计算，在距离地面300km（此距离才有条件达到有载人飞行器的外太空）的太空要看到长城，长城的宽度需达到多少米？（图2）

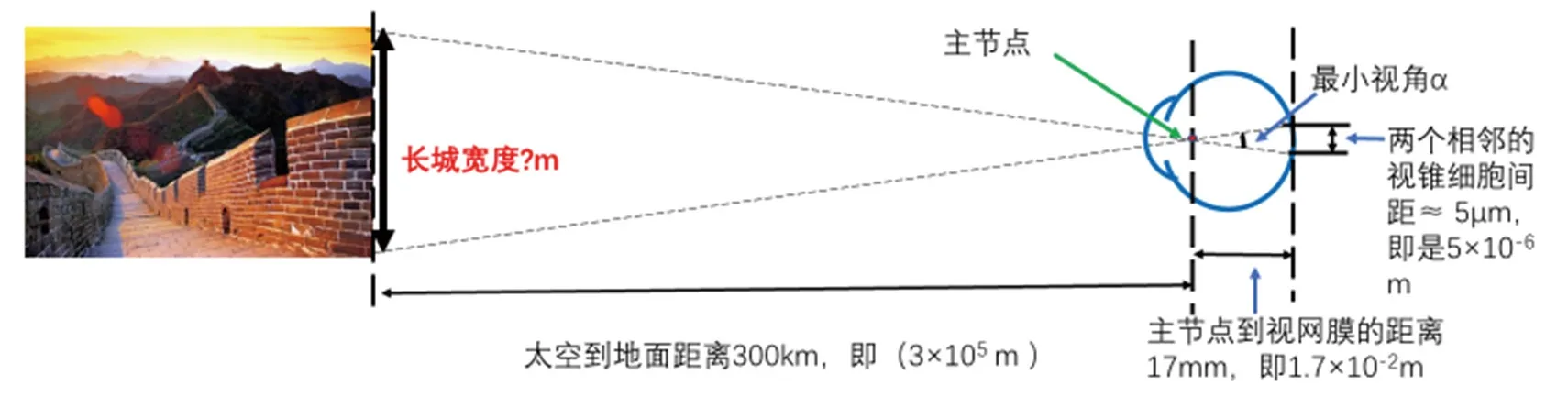
2.1 长城的可视条件

简化眼的光心或称节点（nodal point）在晶状体后，节点到角膜前表面的距离为5.73mm，到后主焦点的距离是17.05mm。

1 π=180°；1°= π/180=0.175弧度（rad）；

1’= °=π/180/60= 0.00029弧度（rad）；

tg1’=tan（π/180/60）=0.000291

Tanα= 5μm/ 17mm= 5×10-6m/ 1.7×10-2m=0.000294（与上述tg1’的值接近）

所以，α=1’。

所以理论上，人眼最小分辨率是1’，即1.0小数视力。假设长城的宽度最小是X米，才能被最小视角1’的人眼在300km的太空看到，那么：

X/3×105= 5×10-6/1.7×10-2（按对顶三角形等比例计算）

X= 3×105×5×10-6/1.7×10-2=88.2m

即长城至少需88.2m宽，才有可能在距地面300km外的太空看到，但是长城的宽度没有88.2m。

2.2 能从太空看到长城的视力条件

如果长城的宽度最多只有10m，那需要多好的视力才能从距地面300km外的太空看到长城呢（图3）？

图3

假设最小视角α能在300km的太空看到10m宽的长城，则

10/ 3×105= Tanα（正切函数的计算公式）

Tanα=3.33×10-5

α= 3.33×10-5弧度=0.0019°=0.114’

1/0.114’=小数视力8.7

所以，小数视力只有达到8.7时，才有可能从太空中看到10m宽的长城，但这个视力是绝对不可能达到的。

3 总结

视力是人眼能分辨的最小视角的倒数。必须在两个受刺激的锥体细胞之间至少夹着一个静止的细胞，才可将两个刺激点区分开，所以人眼的视力有极限。

日常检查视力所用的E视力表，如果是中间一横比较短的“E”（如图4中左图的“E”），1.0的E视标上下两端对人眼形成的夹角其实是3’，而不是1’；如果是中间一横与上下齐平的“E”（如图1中的“E”），实际则是对两个1’视角的缺口的判断，所以看E视力表比较容易，但看E视力表有可能高估了视力（图4）。

C视力表（landolt环），landolt视标是一个带缺口的环，landolt环的缺口定义非常精确，环的缺口为1’视角，所以C视力表（landolt环）比较客观。在E视力表查视力1.5的人如果查C视力表（landolt环）可能正好是1.0。因此，这就解释了为什么我们计算人眼的视力理论极限是1.0，但是很多人视力可以在E视力表上矫正到1.2以上，甚至是2.0的视力。这样就佐证了开始的疑问，在外太空人的肉眼是无法看到长城的。

图4 E视标与C视标的设计差异