五轴数控机床的加工精度建模研究*
2018-08-13范晋伟齐国超陶浩浩李相智
范晋伟 齐国超 陶浩浩 贾 鑫 李相智
(北京工业大学机械工程与应用电子技术学院,北京100124)
数控机床作为机械制造行业中使用面最广、使用量最大的高新技术产品,是精密和超精密加工的重要基础装备[1]。由于近年来,制造行业对具有复杂几何形状和高尺寸精度的机械零部件的需求急剧增加,五轴机床得到越来越广泛的应用[2]。机床的加工精度是衡量机床工作性能的重要指标,而由关键零部件几何误差耦合而成的机床空间误差是影响其加工精度的主要原因[3-5]。因此,研究基于关键零部件几何误差的数控机床精度模型很有意义。
在精度分析方面,人们已经开展了大量的研究工作,并取得了大量的研究成果,产生出多种不同的空间运动误差数学模型建模方法,如几何建模法、误差矩阵法、二次关系模型法、机构学建模法、刚体运动学法和多体系统理论法等[6-8]。Denavit和 Hartenberg等首先利用齐次坐标变换的方法建立了多轴数控机床运动模型。随后 Paul 对该模型进行了改进,为通用误差模型的建立奠定了基础[9]。2012 年刘志峰等[10]利用多体系统运动学理论建立了精密立式加工中心的精度预测模型,通过对典型试件的模拟加工实现了对机床的精度预测,为实现精度分配提供了理论依据。同年,Zhu 等[11]基于多体系统理论提出一种综合几何误差模型、辨识和误差补偿的新方法,通过对五轴加工中心几何误差的辨识,验证了该方法在提高零部件精度方面的有效性。本文基于多体理论对机床整机进行误差分析,并运用齐次坐标变换矩阵对机床的加工精度进行建模,为后续的精度设计工作奠定理论基础。
1 数控机床的结构分析与描述
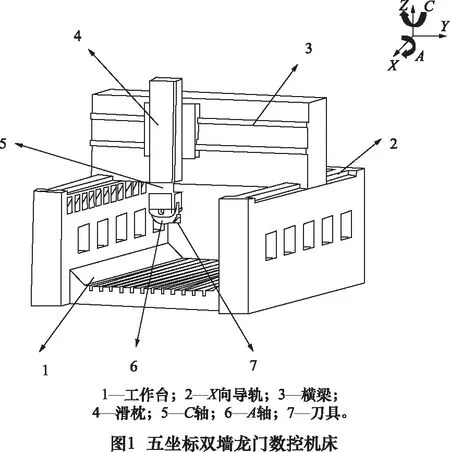
以某机床厂的五坐标双墙龙门数控机床为例。如图1所示,该机床由工作台、X向导轨、溜板、滑枕、C轴、A轴和刀具7个关键零部件构成,其中溜板沿着Y轴方向移动,滑枕沿着Z轴方向移动,A轴和C轴分别绕X轴和Z轴旋转。
基于多体理论,根据零部件间的装配关系,建立如图2所示的拓扑结构图。
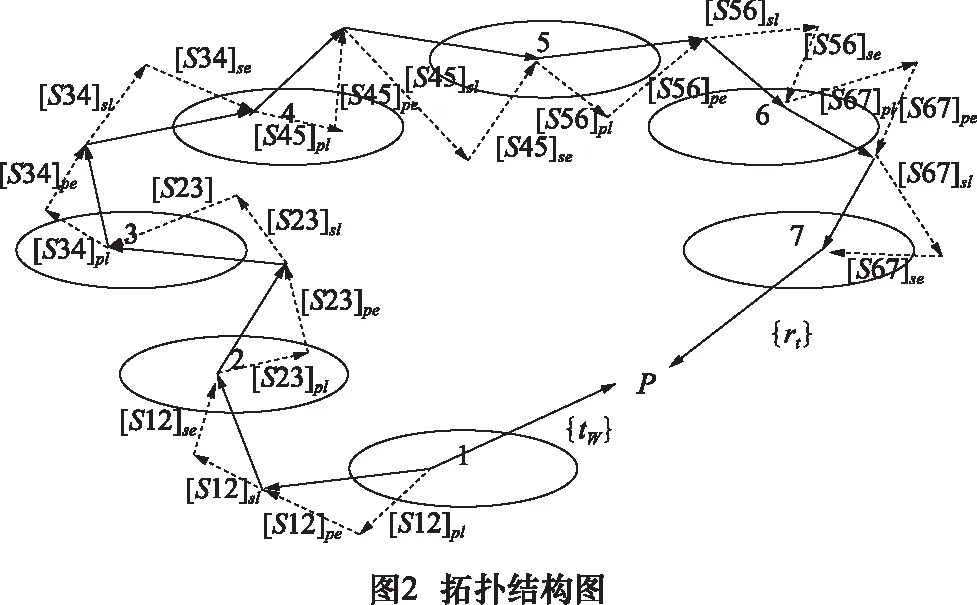
2 数控机床加工精度模型的建立
根据数控机床的7个关键零部件,可以将其分为工件分支和刀具分支两个部分。为机床各个零部件建立自己的右旋笛卡尔坐标系Oj-xjyjzj(j=0,1,2,…),设工件坐标系为Ow-xwywzw,刀具坐标系为Ot-xtytzt,机床坐标系(即工作台坐标系)为O1-x1y1z1。
设Pt为刀具成形点,Vt为刀具姿态(我们把固定在刀具上的矢量来描述刀具在坐标系中的姿态);Pw为刀具的理论刀具路线,Vw为加工工艺确定的刀具姿态。通过以上分析可得,Pt与Vt和Pw与Vw在工作台坐标系O1-x1y1z1中的位置可分别表示为:
·[SLt(j)Lt-1(j)]s·[SLt(j)Lt-1(j)]se}{rt}
(1)
[SLt(j)Lt-1(j)]s·[SLt(j)Lt-1(j)]se}{τt}
(2)
[SLt(j)Lt-1(j)]s·[SLt(j)Lt-1(j)]se}{rw}
(3)
[SLt(j)Lt-1(j)]s·[SLt(j)Lt-1(j)]se}{τw}
(4)
式中:{rt}和{rw}分别为刀具成形点在刀具坐标系Ot-xtytzt和工件坐标系Ow-xwywzw中的位置矩阵表达式;{τt}和{τw}分别为刀具在刀具坐标系Ot-xtytzt和工件坐标系Ow-xwywzw中的位姿矩阵表达式。
在机床的实际切削过程中,刀具成形点实际运动轨迹和刀具位姿都不可避免地会偏离理想运动轨迹和姿态[12]。所以,机床的加工精度模型可以表示为:
{er}=(erxeryerz0)T={Pw}-{Pt}
刀具成形点实际运动位置与理想运动位置误差;{eτ}为:
{eτ}=(eτxeτyeτz0)T={Vw}-{Vt}
刀具实际位姿与理想位姿误差。
3 五轴数控机床几何误差分析与建模实例
以某机床厂的五坐标双墙龙门数控机床为例,基于多体系统理论,分别建立机床各关键零部件的子坐标系,并对机床的几何误差进行分析。利用各关键零部件的相对运动和装配关系建立坐标变换矩阵,从而推导机床加工精度模型。
3.1 五轴双墙龙门数控机床几何误差分析
影响数控机床加工精度的误差源主要有几何误差、热误差、载荷误差和伺服系统误差等[13]。其中几何误差,受环境因素影响小,易于测量,且无论哪种误差,其最终表现形式都可以用前面叙述的几何误差分析运动建模方法来表述。因此本文研究的重点是将几何误差作为基本误差源。五轴双墙龙门数控机床拥有7个关键运动部件,各个关键零部件的误差可分为静态误差和运动误差两个部分[14]。
根据刚体六自由度假设理论,刚体在三维空间中每个轴运动必然会产生六项误差(三项线位移误差、三项角位移误差),五个轴共有30项运动误差;此外3个平动轴之间两两存在3项垂直度误差,并且A轴与Y轴和Z轴以及C轴与X轴和Y轴之间存在4项垂直度误差,即7项静态误差。所以,五轴双墙龙门数控机床的几何误差参数一共37项,如表1所示。
3.2 机床关键零部件子坐标系的建立
在初始条件下各运动部件的体坐标系与其运动参考坐标系重合,也就是在初始条件下只要确定了某运动部件的运动参考系方位也就确定了其体参考坐标系的方位。
表1 五轴数控机床37项几何误差
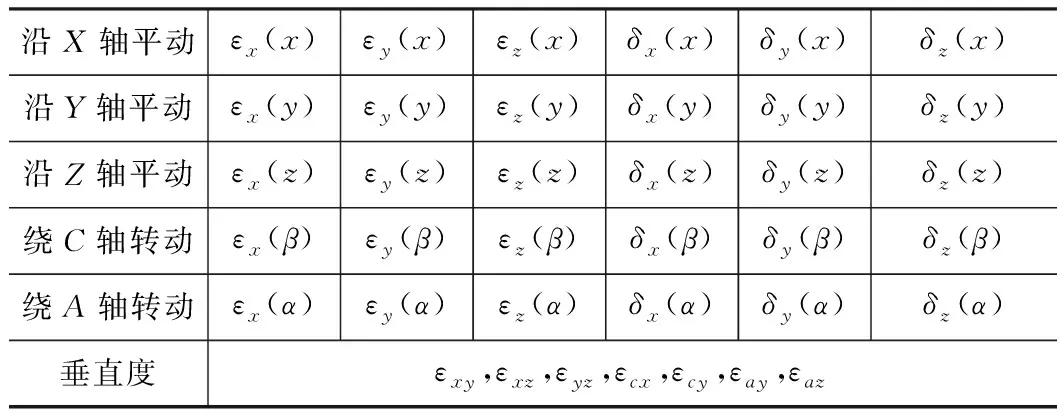
沿X轴平动εx(x)εy(x)εz(x)δx(x)δy(x)δz(x)沿Y轴平动εx(y)εy(y)εz(y)δx(y)δy(y)δz(y)沿Z轴平动εx(z)εy(z)εz(z)δx(z)δy(z)δz(z)绕C轴转动εx(β)εy(β)εz(β)δx(β)δy(β)δz(β)绕A轴转动εx(α)εy(α)εz(α)δx(α)δy(α)δz(α)垂直度εxy,εxz,εyz,εcx,εcy,εay,εaz
首先确定各个子坐标系的方向:选取机床坐标系(也就是工作台坐标系)的方向为基准方向,令机床坐标系和X向导轨的运动参考坐标系与基准坐标系方向一致;令基准坐标系绕其Y轴转动垂直度εxz后的坐标系为Y向溜板(B3)的运动参考坐标系;令Y向溜板(B3)的运动参考坐标系分别绕其X、Y轴转动εzy、εxy后的坐标系为Z向滑枕(B4)的运动参考坐标系;令Z向滑枕(B4)的运动参考坐标系绕X、Y轴转动εyc、εxc后为C轴(B5)的运动参考坐标系;令床身的运动参考坐标系分别绕Y、Z轴转过εyc、εyc后为A轴(B6)的运动参考坐标系。
其次,确定各个子坐标系之间的位置:B6体与刀具参考坐标系均位于A轴旋转中心轴与刀具中心轴交点处(O1);其它个体的子坐标系均位于机床坐标系原点处。
3.3 特征矩阵
在初始条件下,O1在机床坐标系下坐标为(q1xq1yq1z1)T,工件坐标系相对于工作台坐标系的位置为{Tw}。综上分析,各关键零部件特征矩阵如下所示:
[S12]p=[S12]pe=E4×4
[S23]p=E4x×4
[S34]p=E4×4
[S45]p=E4×4
3.4 五轴双墙龙门数控机床加工精度模型的建立
初始条件下,实际刀具中心在刀具坐标系的位置为{rt}=(0 0 -L1)T,L为刀具长度,实际刀具位姿在刀具坐标系中表达式为{τt}=(0 0 -1 0)T;在工件坐标系下,理论刀具路线为{rw}=(xwywzw1)T,理论刀具位姿{τw}=(xvyvzv0)T,由此可以得到在工作台坐标系下,刀具实际成形点的位置为:
[SLt(j)Lt-1(j)]s·[SLt(j)Lt-1(j)]se]{rt}
=[S12]p·[S12]pe·[S12]s·[S12]se·[S23]p·[S23]pe·
[S23]s·[S23]se·[S34]p·[S34]pe·[S34]s·[S34]se·
[S45]p·[S45]pe·[S45]s·[S45]se·[S56]p·[S56]pe·
[S56]s·[S56]se·[S67]p·[S67]pe·[S67]s·[S67]se·{rt}
(5)
刀具实际位姿表达式为:
[SLt(j)Lt-1(j)]s·[SLt(j)Lt-1(j)]se]{τt}
=[S01]p·[S01]pe·[S01]s·[S01]se·[S12]p·[S12]pe
·[S12]s·[S12]se·[S23]p·[S23]pe·[S23]s·[S23]se·
[S34]p·[S34]pe·[S34]s·[S34]se·[S45]p·[S45]pe·
[S45]s·[S45]se·[S56]p·[S56]pe·[S56]s·[S56]se{τt}
(6)
理论刀具路线在工作台坐标系中的位置为:
[SLt(j)Lt-1(j)]s·[SLt(j)Lt-1(j)]se}{rw}=Tw{rw}
(7)
理论刀具路线在工作台坐标系中的位姿为:
[SLt(j)Lt-1(j)]s·[SLt(j)Lt-1(j)]se}{τw}=Tw{τw}
(8)
所以,刀具切削点实际运动位置与理想运动位置误差:
{er}=(erxeryerz0)T={Pw}0-{Pt}0
(9)
将变换矩阵代入方程(5)、(7)和(9)中,消去高阶无穷小量,可得:
erx=δx(x)+δx(y)-qwx-xw+x+δx(c)×cos(c)+
δy(c)×sin(c)-ezx×y+qtx×cos(c)
(10)
ery=δy(x)+δy(y)-qwy-yw+y-δx(c)×sin(c)+δy(c)×
cos(c)-q1z×cos(c)
(11)
erz=δz(x)+δz(y)-qwz-zw+z+cos(A)-sin(A)×exc+δz(z)
(12)
刀具实际位姿与理想位姿误差:
{eτ}=(eτxeτyeτz0)T={Vw}0-{Vt}0,
(13)
将变换矩阵代入方程(6)、(8)和(13),经整理消去高阶无穷小量,可得:
{eτx}=cos(α)×[-εy(y)-εy(x)-cosγ]-εxz+εyc×sinγ+
εx(γ)×sinγ-εxc×cosγ-εy(z)
(14)
{eτy}=-εx(α)×sin(α)-εx(γ)×sinγ-εy(γ)×sinγ-εx(z)-
εx(γ)×cosγ+cosα×[-εx(z)+εx(γ)×cosγ]
(15)
{eτz}=-cosα-zv+cosγ×[-εy(z)-εy(y)-εy(x)]-εy(α)×cosα+
sinα×{cosγ×[εx(x)+εx(y)+εx(z)-εxz]}+εx(α)×sinα
(16)
从而得到五轴双墙龙门机床的加工精度模型。
3.5 实验验证
本文利用双频激光干涉仪和双球杆仪,并结合九线法,辨识出该机床的37项几何误差。在测量机床的定位误差中,为了降低试验的难度,试验时滑动横梁静止不动,垂直滑枕沿活动横梁导轨运动,且A轴和C轴的转角设置为0°,在垂直滑枕工作行程范围内取20个测量点,通过试验测量得到垂直滑枕运动到测量点位置处切削点x、y、z三个方向上的位移误差以及分别与之对应的37项几何误差变量。
表2 几何误差传递模型性能指标
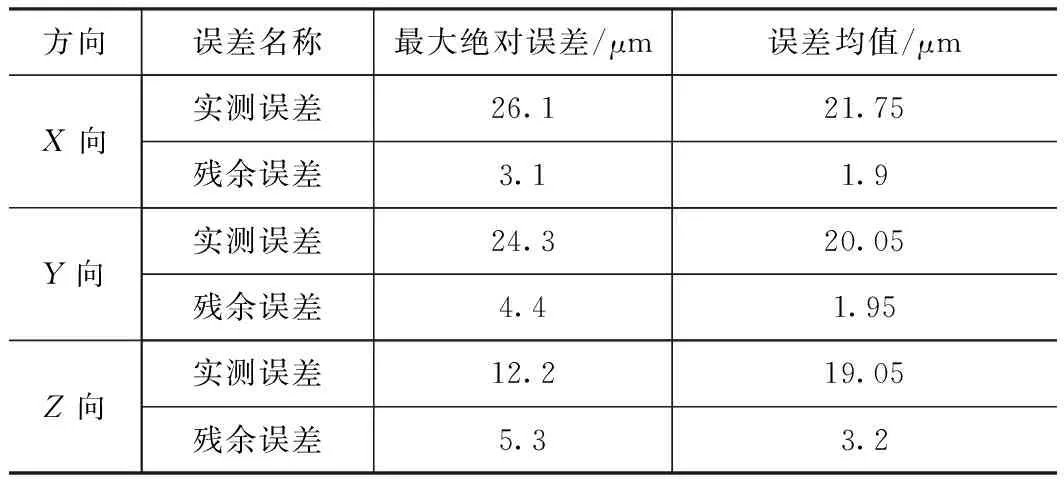
方向误差名称最大绝对误差/μm误差均值/μmX向实测误差26.121.75残余误差3.11.9Y向实测误差24.320.05残余误差4.41.95Z向实测误差12.219.05残余误差5.33.2
将测量的37项几何误差变量带入式(10)、(11)、(12)中,计算出刀具切削点在X、Y、Z三个方向的误差并将其与试验测量的结果进行比对,检验模型的预测精度。结果如图3~5及表2所示。
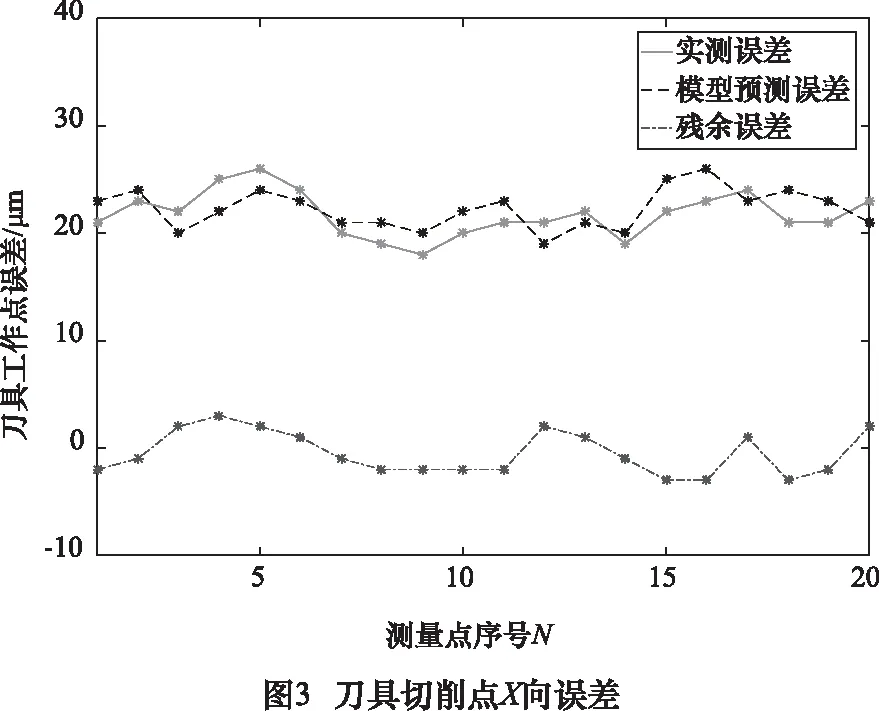
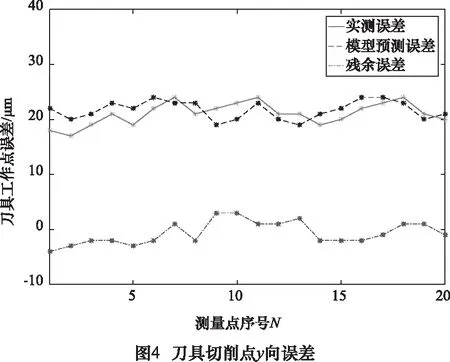
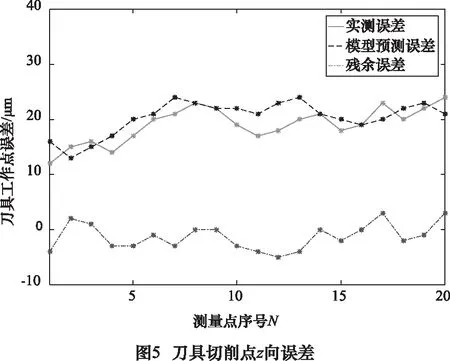
其中,残余误差=实测误差-模型预测误差。
由表2可知,本文建立的机床加工精度模型有比较理想的预测性能。
4 结论
(1)通过对五轴双墙龙门数控机床进行结构分析,并利用拓扑结构对该机床结构进行描述,将机床简化为7个关键零部件,并对每个运动部件建立子坐标系和运动参考坐标系。
(2)对五轴双墙龙门数控机床的几何误差进行分析,得出机床37项几何误差。
(3)利用多体系统运动学理论推导出机床各运动部件之间的相对运动坐标变换矩阵,进一步推导出机床的加工精度模型,为今后机床加工精度的预测工作打下基础。
