k次Herschel—师连通圈网络

师海忠，陈璐璐



k次Herschel—师连通圈网络

师海忠，陈璐璐

（西北师范大学 数学与统计学院，甘肃 兰州 730070）

互连网络是超级计算机的重要组成部分，片上互连网络是当前研究的热点课题之一。2010年师海忠提出互连网络的正则图连通圈网络模型。在这篇文章中利用此模型设计出了k次Herschel-师连通圈网络HSCC(1,k),证明了HSCC(1,0)是3正则3连通平面Hamiton图，且HSCC(1,k)是3正则3连通平面Hamiton图。利用笛卡尔乘积设计出了互连网络HSCC(1,k)×K2和HSCC(1,k)´Cm，进一步研究了HSCC(1,k)´K2和HSCC(1,k)´Cm的一些性质。

HSCC(1,k)；Hamilton图；笛卡尔积；完美对集

0 引言

互连网络是超级计算机的重要组成部分，片上互连网络是当前研究的热点课题之一，它的性能在某种程度上决定着超级计算机的性能。互连网络通常被模型化为一个图，图的结点对应处理机，图的边对应通信全过程。各种已有互连网络参见[1,2,4-12]。根据师海忠在中国运筹会第十届学术交流会上提出的超级计算机多种互连网络统一体——正则连通圈网络，且它的度为3。在这篇文章中，师海忠设计出了互连网络HSCC(1,0)：将Herschel图经过4度顶点用4圈代替、3度顶点用3圈代替原来顶点构造了新的网络HSCC(1,0)，陈璐璐证明了HSCC(1,0)是3正则3连通平面Hamilton图，师海忠进一步提出了k次Herschel—师连通圈网络HSCC(1,k)：用3长的圈代替HSCC(1,0)中的每个顶点构造了新的网

络HSCC(1,1)，重复k次，我们得到的新的网络HSCC(1,k)，陈璐璐证明了k次Herschel—师连通圈网络为3正则3连通平面Hamilton图。师海忠还设计出了HSCC(1,k)´K2和HSCC(1,k)´Cm，并提出了如下猜想：

猜想1：HSCC(1,k)´k2是边不交的两个Hamilton的并；

猜想2：HSCC(1,k)´Cm（k=0, m≥3）是边不交的两个Hamilton圈和一个完美对集的并。

陈璐璐证明了HSCC(1,0)´k2是一个边不交的Hamilton圈和两个完美对集的并，还给出了HSCC (1,k)´K2和HSCC(1,k)´Cm的一些性质。

1 基本概念

定义1[1]G的Hamilton圈是指包含G的每个顶点的圈。

定义2[1]一个图若包含Hamilton圈，则称这个图是Hamilton图。

定义3[1]若G至少有一对相异的不相邻顶点，则G所具有的k顶点割中最小的k，称为G的连通度，记为k(G);否则定义k(G)为v－1。于是，当G是平凡的或不连通时，k(G)=0。若k(G)≥k，则称G为k连通的。

定义4[1]称图G是k正则的，如果对所有的v∈V,有d(v)=k。

定义5 用4长的圈代替Herschel图中的4度顶点、3长的圈代替Herschel图中的3度顶点，我们得到新的网络HSCC(1,0)；再用3长的圈代替HSCC(1,0)中的每个顶点，我们得到新的网络HSCC (1,1)；重复k次，我们得到新的网络HSCC(1,k)。

定义6[1]若一个图具有这样的一个图形，它的边仅在端点处相交，则该图称为平面图。

定义7[1]设M是E的一个子集，它的元素是G中的连杆，并且这些连杆中的任意两个在G中均不相邻，则称M为G的对集（或匹配）；M中一条边的两个端点称为在M下是匹配的。若对集M的某条边与顶点v关联，则称M饱和顶点v，并且称v是M饱和的，否则称v是M非饱和的。若G的每个顶点均为M饱和的，则称M为G的完美对集。

定义8[2]设G1=(V1,E1)和G2=(V2,E2)是两个无向图。G1和G2的笛卡尔乘积是无向图，记为G1´G2,其中V（G1´G2）=V1´V2,两个不同的顶点x1x2和y1y2(其中x1,y1∈V（G1），x2,y2∈V（G2）)相邻当且仅当或者x1=y1，且x2y2∈E（G2），或者x2=y2，且x1y1∈E（G1）。G1和G2称为G1´G2的因子。

定义9 将k次Herschel-师连通圈网络HSCC(1,k)与K2作笛卡尔乘积生成的网络为HSCC (1,k)´K2；k次Herschel-师连通圈网络HSCC(1,k)与m长的圈Cm作笛卡尔乘积生成的网络为HSCC (1,k)´Cm。

2 主要结果

2.1 Herschel图及性质

引理[1]Herschel图是非Hamilton图。

2.2 k次Herschel-师连通圈网络

2.2.1 0次Herschel-师连通圈网络

构造0次Herschel-师连通圈网络HSCC(1,0)：在H中，4度顶点用4长的圈代替、3度顶点用3长的圈代替，我们将得到新的网络HSCC(1,0)。

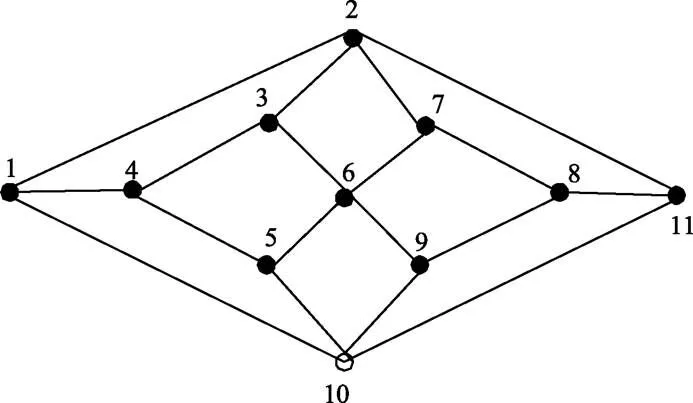
图1 H

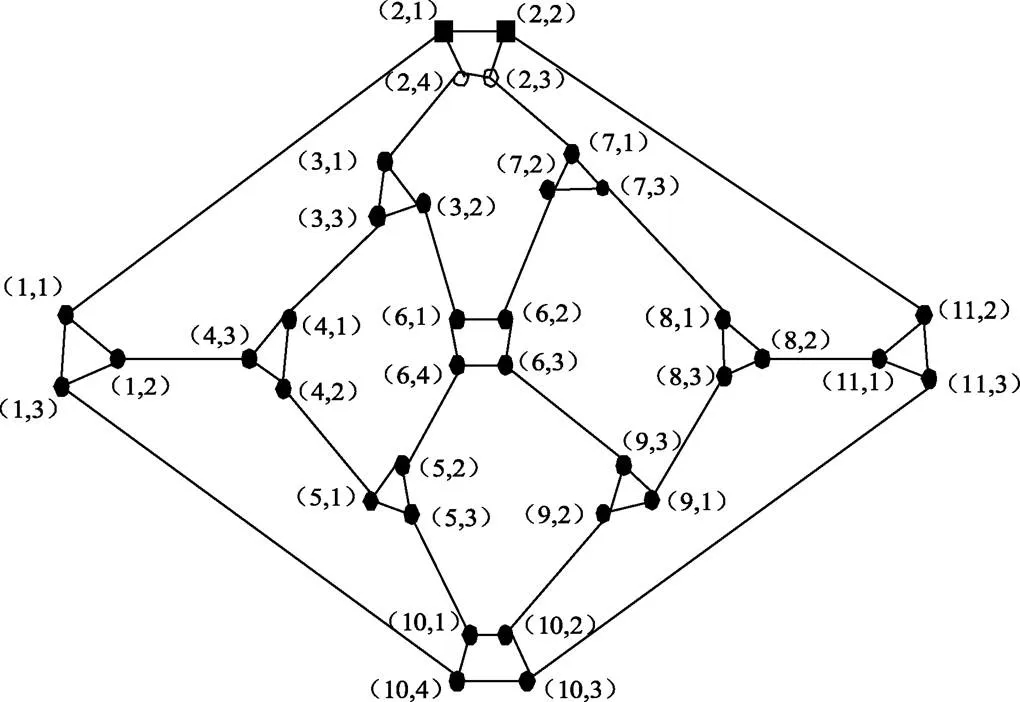
图2 0次Herschel-师连通圈网络HSCC(1,0)

由图2知

定理1 HSCC(1,0)具有如下一些性质：

(1)HSCC(1,0)是平面图；

(2)HSCC(1,0)是3正则的；

(3)HSCC(1,0)是3连通的；

(4)HSCC(1,0)是Hamilton图。

证明：（1）、（2）显然

（3）因为HSCC(1,0)中每个顶点的度均为3，则它的最小度d=3。

又由于k≤d（定理[1]），可得，图HSCC(1,0)的连通度k≤3。

由于图HSCC(1,0)是非平凡的且是连通的，则k≠0。

若k=1，即HSCC(1,0)所具有的k顶点割中最小的为1，

由图2知，去掉图HSCC(1,0)中任何一点后得到的图仍是连通的，因此k≠1。

若k=2，即HSCC(1,0)所具有的k顶点割中最小的为2，

由图2知，去掉图HSCC(1,0)中任何两点后得到的图仍是连通的，因此k≠2。

从而k＞2，又由于k≤3，故k=3。即HSCC(1,0)是3连通的。

（4）图HSCC(1,0)中的Hamilton圈：

（4,1）-（3,3）-（3,2）-（3,1）-（2,4）-（2,1）-（2,2）-（2,3）-（7,1）-（7,2）-（7,3）-（8,1）-（8,3）-（8,2）-（11,1）-（11,2）-（11,3）-（10,3）-（10,2）-（9,2）-（9,1）-（9,3）-（6,3）-（6,2）-（6,1）-（6,4）-（5,2）-（5,1）-（5,3）-（10,1）-（10,4）-（1,3）-（1,1）-（1,2）-（4,3）-（4,2）-（4,1）

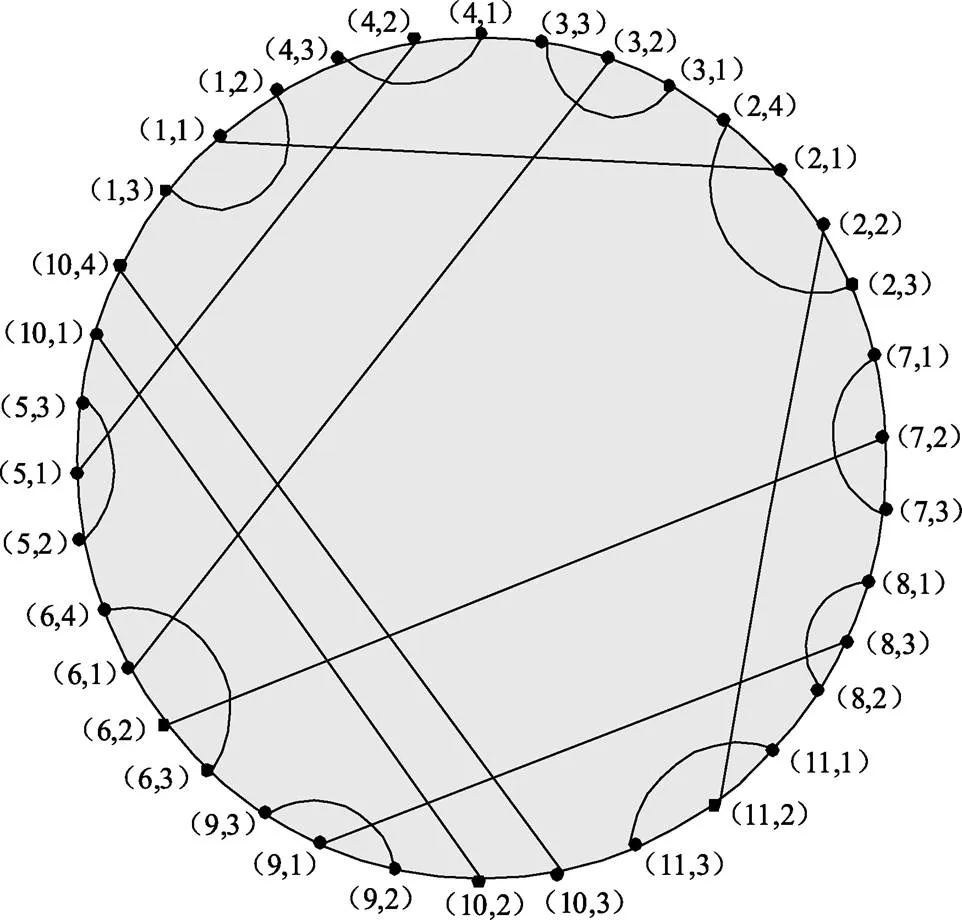
图3 HSCC(1,0)的圈表示

从而HSCC(1,0)是Hamilton图。

2.2.2 1次Herschel-师连通圈网络

构造1次Herschel-师连通圈网络HSCC(1,1)：用3长的圈代替HSCC(1,0)中的每个顶点，我们将得到新的网络HSCC(1,1)。

由图4知

定理2 1次Herschel-师连通圈网络HSCC(1,1)具有如下一些性质：

（1）HSCC(1,1)是平面图；

（2）HSCC(1,1)是3正则的；

（3）HSCC(1,1)是3连通的；

（4）HSCC(1,1)是Hamilton图。

证明：（1）、（2）显然

（3）因为HSCC(1,1)中每个顶点的度均为3，则它的最小度d=3。

从而，图HSCC(1,1)的连通度k≤3。

由于图HSCC(1,1)是非平凡的且是连通的，则k≠0。

若k=1，即HSCC(1,1)所具有的k顶点割中最小的为1，

由图4知，去掉图HSCC(1,1)中任何一点后得到的图仍是连通的，

因此k≠1。

若k=2，即HSCC(1,1)所具有的k顶点割中最小的为2，

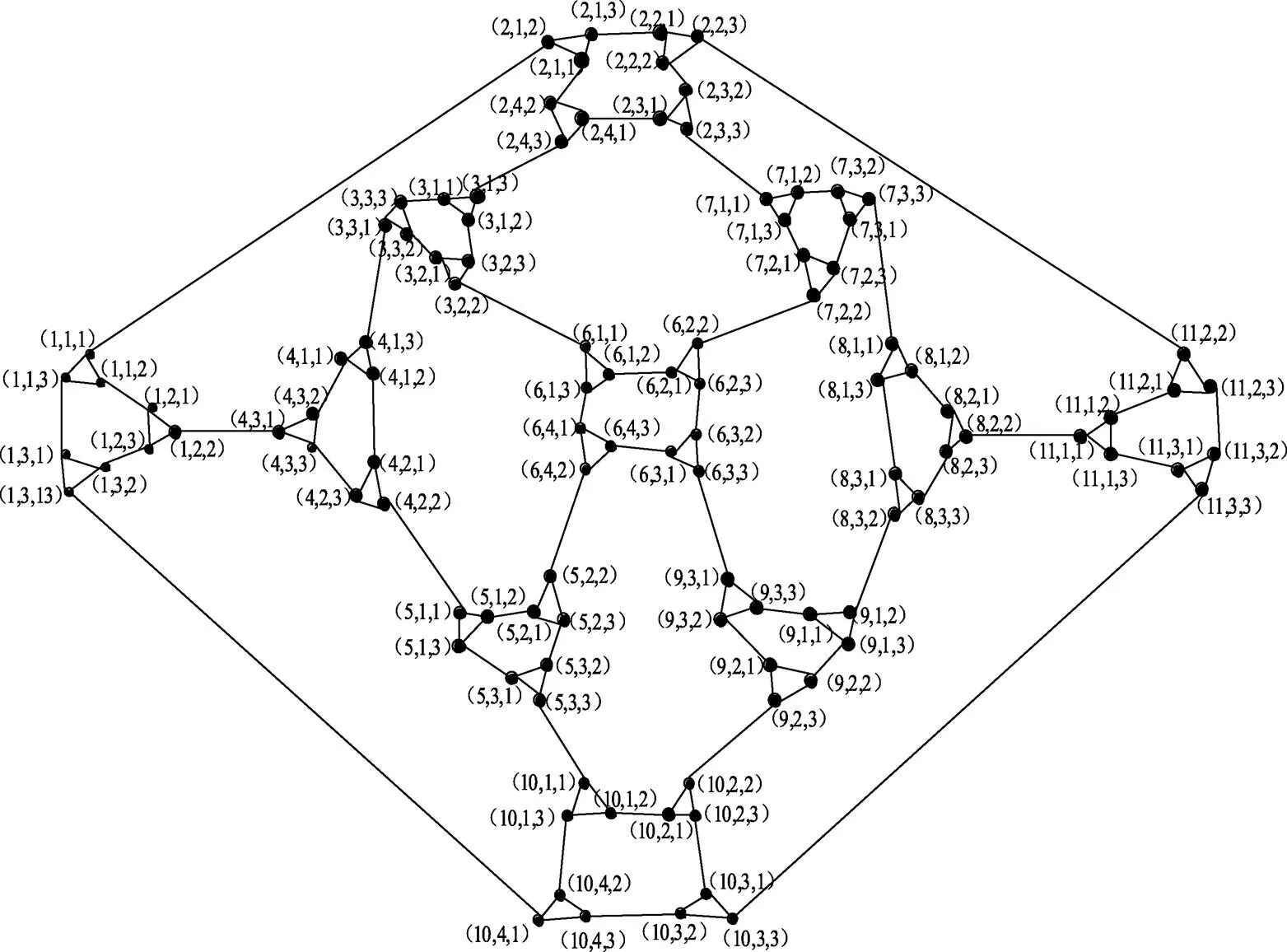
图4 1次Herschel-师连通圈网络HSCC(1,1)

由图4知，去掉图HSCC(1,1)中任何两点后得到的图仍是连通的，

因此k≠2。从而k＞2，又由于k≤3，故k=3。

即HSCC(1,1)是3连通的。

（4）图HSCC(1,1)中的Hamilton圈：

（4,1,1）-（4,1,3）-（3,3,1）-（3,3,3）-（3,3,2）-（3,2,1）-（3,2,2）-（3,2,3）-（3,1,2）-（3,1,1）-（3,1,3）-（2,4,1）-（2,4,2）-（2,4,3）-（2,1,1）-（2,1,2）-（2,1,3）-（2,2,1）-（2,2,3）-（2,2,2）-（2,3,2）-（2,3,1）-（2,3,3）-（7,1,1）-（7,1,2）-（7,1,3）-（7,2,1）-（7,2,2）-（7,2,3）-（7,3,1）-（7,3,2）-（7,3,3）-（8,1,1）-（8,1,2）-（8,1,3）-（8,3,1）-（8,3,2）-（8,3,3）-（8,2,3）-（8,2,1）-（8,2,2）-（11,1,1）-（11,1,3）-（11,1,2）-（11,2,1）-（11,2,2）-（11,2,3）-（11,3,2）-（11,3,1）-（11,3,3）-（10,3,3）-（10,3,2）-（10,3,1）-（10,2,3）-（10,2,1）-（10,2,2）-（9,2,3）-（9,2,1）-（9,2,2）-（9,1,3）-（9,1,2）-（9,1,1）-（9,3,3）-（9,3,2）-（9,3,1）-（6,3,3）-（6,3,1）-（6,3,2）-（6,2,3）-（6,2,2）-（6,2,1）-（6,1,2）-（6,1,1）-（6,1,3）-（6,4,1）-（6,4,3）-（6,4,2）-（5,2,2）-（5,2,3）-（5,2,1）-（5,1,2）-（5,1,1）-（5,1,3）-（5,3,1）-（5,3,2）-（5,3,3）-（10,1,1）-（10,1,2）-（10,1,3）-（10,4,2）-（10,4,3）-（10,4,1）-（1,3,3）-（1,3,2）-（1,3,1）-（1,1,3）-（1,1,1）-（1,1,2）-（1,2,1）-（1,2,3）-（1,2,2）-（4,3,1）-（4,3,2）-（4,3,3）-（4,2,3）-（4,2,2）-（4,2,1）-（4,1,2）-（4,1,1）

从而图HSCC(1,1)是Hamilton图。

表1 图HSCC(1,1)中Hamilton圈中各顶点与相邻的点

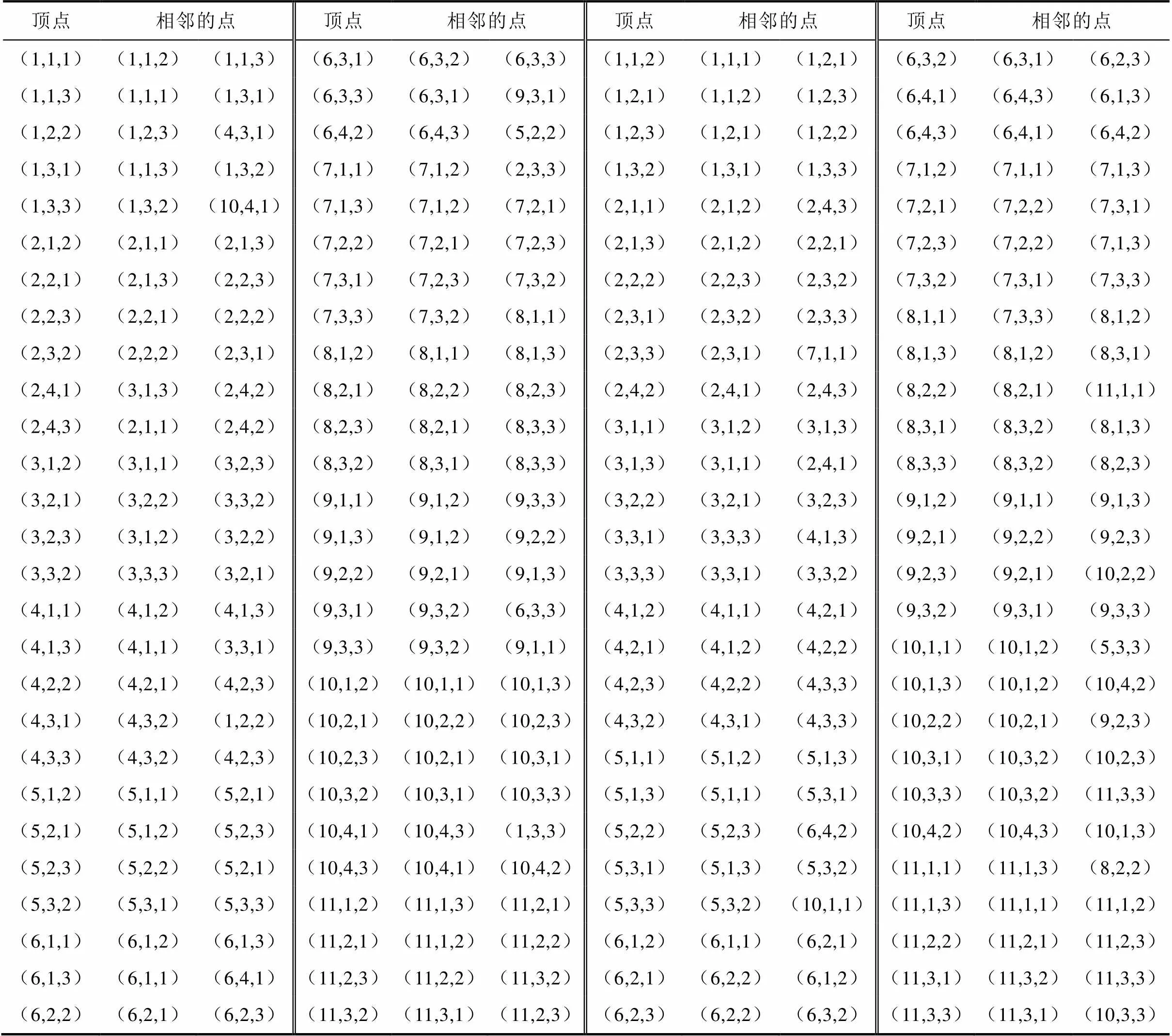
Tab.1 Each vertex and adjacent point in Hamilton circle in HSCC(1,1)

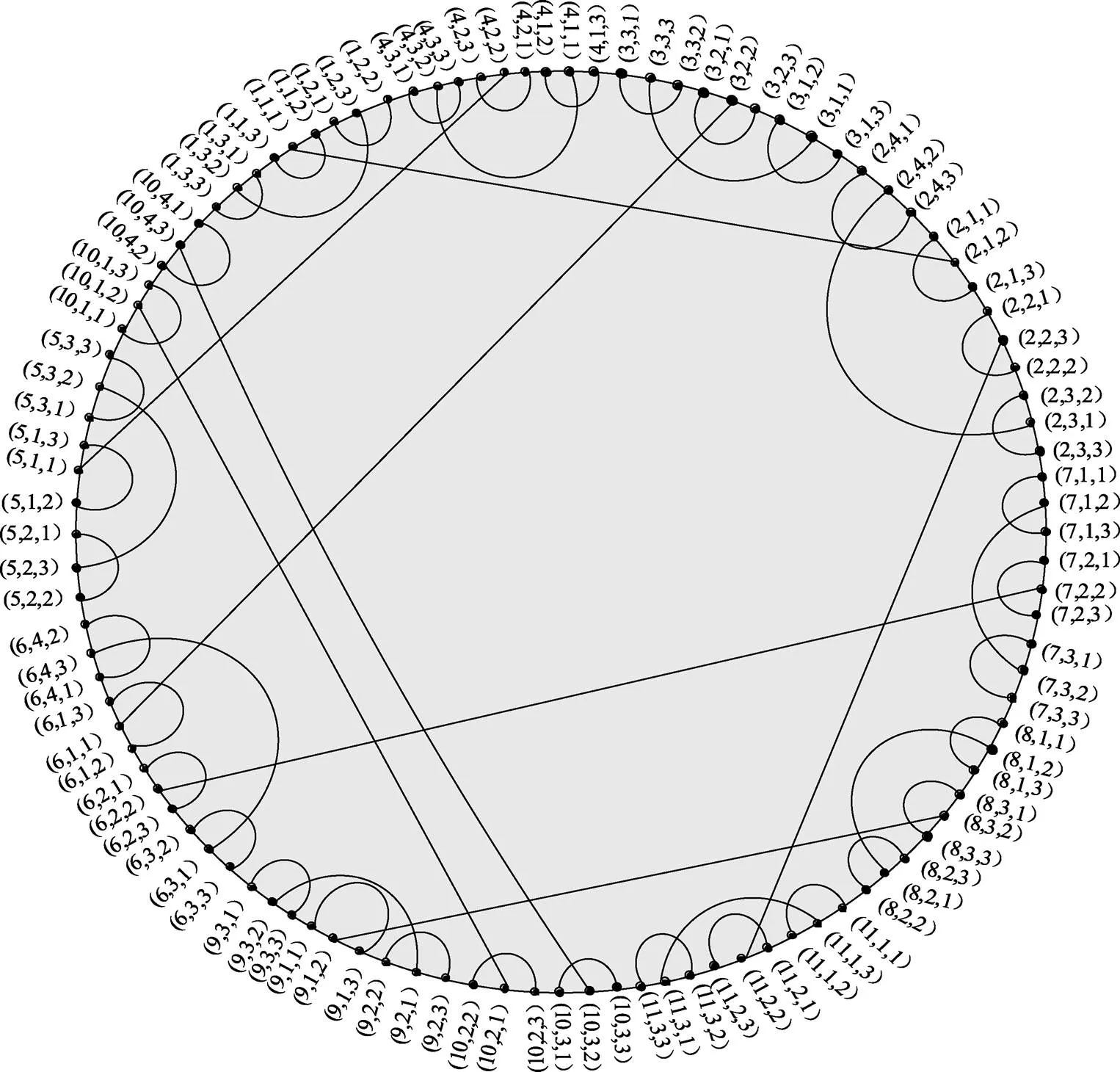
图5 HSCC(1,1)的圈表示

2.2.3 k次Herschel-师连通圈网络

构造k次Herschel-师连通圈网络HSCC(1,k)：用3长的圈代替HSCC(1,1)中的每个顶点构造了新的网络HSCC(1,2)，用3长的圈代替HSCC(1,2)中的每个顶点构造了新的网络HSCC(1,3)，重复k次，我们得到的新的网络HSCC(1,k)。

定理3 k次Herschel-师连通圈网络HSCC(1,k)具有如下一些性质：

（1）HSCC(1,k)是平面图；

（2）HSCC(1,k)是3正则的；

（3）HSCC(1,k)是3连通的；

（4）HSCC(1,k)是Hamilton图。

证明：（1）、（2）、（3）显然

（4）下证HSCC（1,k）是Hamilton图（数学归纳法）。

当k=1时，HSCC(1,k)即为HSCC(1,1)是Hamilton图，则结论成立。

假设当k=r-1时，结论成立，即HSCC(1,r-1)是Hamilton图，

也即HSCC(1,r-1）有一个Hamilton圈记为CHSCC(1,r-1)。取CHSCC(1,r-1)中的任意顶点b、c、d是与a相邻的三个顶点，则CHSCC(1,r-1)中必含边ab、ac、ad中的两条边，假设CHSCC(1,r-1)中含边ab、ac（见图6）。

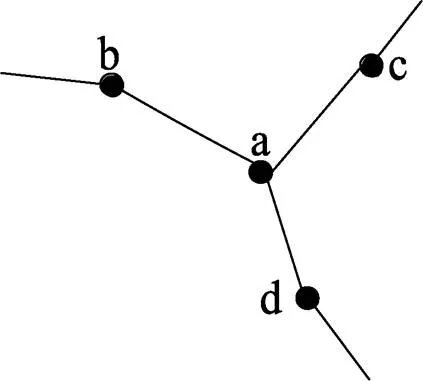
图6 HSCC(1,r-1)的局部表示

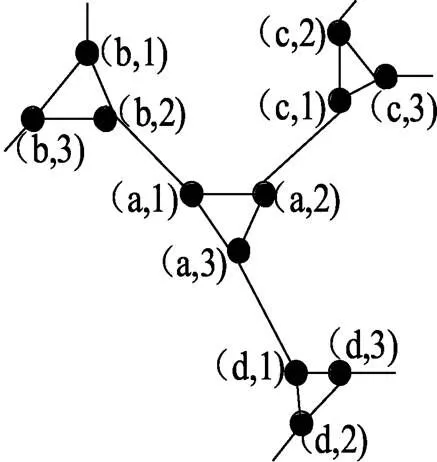
图7 HSCC(1,r)的局部表示

当k=r时，即当用3长的圈代替CHSCC(1,r-1)中的每一个顶点时，假设用圈（a,1）-（a,2）-（a,3）-（a,1）代替a，用圈（b,1）-（b,2）-（b,3）-（b,1）代替 b, 用圈（c,1）-（c,2）-（c,3）-（c,1）代替c, 用圈（d,1）-（d,2）-（d,3）-（d,1）代替d,则a、b、c、d四点变化后的图为图7。用路P=（（b,2），（a,1）, (a,3）, (a,2）, (c,1）)代替路（bac）后，得到的圈仍为Hamilton圈，同理，CHSCC(1,r-1)中的任意点都有如上性质。从而CHSCC(1,r-1)中所有点用3长的圈代替，且用上面方式代替原来的路，得到的圈CHSCC(1,r)即为HSCC(1,r)的一个Hamilton圈。

综上所述，由数学归纳法知HSCC(1,k)是Hamilton图。

2.3 k次Herschel-师连通圈网络的3维变体

2.3.1 HSCC（1,k）与K2的笛卡尔积网络

根据文献[6]的思想设计出了新的互连网络HSCC(1,k)´K2

定理4 HSCC(1,k)´K2可以分解成一个边不交的Hamilton圈和两个完美对集的并。

图HSCC(1,0)´K2的Hamilton圈：

001-002-004-005-006-007-008-009-010-011-012-013-014-015-016-017-018-019-020-021-022-023-024-025-026-027-028-029-030-031-032-033-034-035-036-003-103-136-135-134-133-132-131-130-129-128-127-126-125-124-123-122-121-120-119-118-117-116-115-114-113-112-111-110-109-108-107-106-105-104-102-101-001

图8 HSCC(1,0)与K2的笛卡尔积网络HSCC(1,0)´K2

图HSCC(1,0)´K2的两个完美对集：

（1）002-003，001-011，004-006，007-009，005-034，008-030，010-013，012-021，014-016，029-015，031-028, 017-019，020-022，027-025，026-018，024-035，023-036，032-033，102-103，101-111，104-106，107-109，110-113，112-121，105-133，108-130，110-113，114-116，117-119，120-122，118-126，125-127，128-131，132-134，124-135，123-126

（2）001-003，101-103，002-102，004-104，005-105，006-106，007-107，008-108，009-109，010-110，011-111，012-112，013-113，014-114，015-115，016-116，017-117，018-118，019-119，020-120，021-121，022-122，023-123，024-124，025-125，026-126，027-127，028-128，029-129，030-130，031-131，032-132，033-133，034-134，035-135，036-136

定理5 k次Herschel-师连通圈网络HSCC(1,k)与K2的笛卡尔积网络HSCC(1,k)´K2的一些性质：

（1）HSCC(1,k)´K2是4正则4连通的；

（2）HSCC(1,0)´K2有72个顶点，有144条边；

（3）HSCC(1,k)´K2（k≥1）有72´3k个顶点，有108＋36´3k+1条边；

（4）HSCC(1,0)´K2是Hamilton图。

证明：（1）由定理3知HSCC(1,k)是3正则3连通的，而K2是1正则1连通的，

故HSCC(1,k)´Cm是4正则4连通的。

（2）、（3）显然

（4）由定理4知HSCC(1,0)´K2是Hamilton图

猜想1仍是开的

2.3.2 HSCC(1,k)与Cm的笛卡尔积网络

根据文献[6]的思想设计出了新的互连网络HSCC(1,k)´Cm

定理6 k次Herschel-师连通圈网络HSCC(1,k)与Cm的笛卡尔积网络HSCC(1,k)´Cm的一些性质：

（1）HSCC(1,k)´Cm是5正则5连通的；

（2）HSCC(1,0)´Cm有36 m个顶点，有108+ 36 m条边；

（3）HSCC(1,k)×Cm（k≥1）有36 m´3k个顶点，有108+72 m´3k条边；

（4）HSCC(1,0)´C3是Hamilton图。

证明：（1）由定理3知HSCC(1,k)是3正则3连通的，而Cm是2正则2连通的，

故HSCC(1,k)´Cm是5正则5连通的。

（2）、（3）显然

（4）HSCC(1,0)×C3的Hamilton圈：

001-002-004-005-006-007-008-009-010-011-012-013-014-015-016-017-018-019-020-021-022-023-024-025-026-027-028-029-030-031-032-033-034-035-036-003-103-136-135-134-133-132-131-130-129-128-127-126-125-124-123-122-121-120-119-118-117-116-115-114-113-112-111-110-109-108-107-106-105-104-102-202-204-205-206-207-208-209-210-211-212-213-214-215-216-217-218-219-220-221-222-223-224-225-226-227-228-229-230-231-231-232-233-234-235-236-203-201-101-001

故HSCC(1,0)´C3是Hamilton图。

猜想2仍是开的

4 结论

本文给出了HSCC(1,k)（k≥0）的定义以及一些性质，证明了HSCC(1,k)是Hamilton图，以及HSCC(1,k)与K2、HSCC(1,k)与Cm的笛卡尔积的一些性质。

[1] BONDY J A and MURTY U S R. Graph Theory with Applications[M]. Macmillan Press Ltd, London and Basingstlke, 1976.

[2] 徐俊明. 组合网络理论[M]. 北京: 科学出版社, 2007.

[3] Xu Junming .A First Course in Graph Theory[M]. Science Press, Beijing, 2015.

[4] 师海忠. 正则连通圈: 多种互连网络的统一模型[C]. 北京: 中国运筹学会第十一届学术交流会文集, 2010: 202-208.

[5] 师海忠. 几类新的笛卡尔乘积互连网络[J]. 计算机科学, 2013, 40(6A): 265-270.

[6] Shi, H. and Shi, Y. (2015) A New Model for Interconnection Network:K-Hierarchcal Ring and R-Layer Graph Network. http://vdisk.weibo.com/s/dlizJyferZ-ZI.

[7] Shi, H. and Shi, Y. (2015) A Hierarchcal Ring Group- theoretic Model for Interconnection Networks. http://vdisk. weibo.com/s/dlizJyfeBX-2J.

[8] Shi, H. and Shi, Y. (2015) Cell-Breading Graph Model for Interconnection Networks. http://vdisk.weibo.com/s/dlizJyfesb05y

[9] 张欣, 师海忠. 交叉立方体连通圈网络的Hamilton分解[J]. 软件, 2015, 36(8): 92-98.

[10] 常立婷, 师海忠. 基于超立方体和圈的细胞分裂生长网络及其性质[J]. 软件. 2017, 38(9): 141-149.

[11] 师海忠, 汪生龙. 关于煎饼网络及层次环煎饼网络的几个猜想[J]. 软件. 2018(01): 94-100.

[12] 胡艳红, 师海忠. 关于冒泡排序连通圈网络猜想的一个注记[J]. 软件. 2016(01): 97-100.

k Herschel – Shi Connected Cycles Networks

SHI Hai-zhong, CHEN Lu-lu

(College of Mathematics and Statistics, Northwest Normal University, Lanzhou Gansu 730070, China)

An Interconnection network is an important part of a supercomputer. On-chip interconnection network is one of the hot topics in the current research.In 2010,Hai-zhong Shi proposed the model of regular graph connected cycles.In this paper, we design the network model of regular graphs of interconnected networks HSCC(1,k) and prove that HSCC(1,0) is a 3-regular 3-connected planar Hamilton graph,and HSCC(1,k) is a 3-regular 3-connected planar Hamilton graph.By using the Cartesian product, the interconnect network HSCC(1,k)×K2and HSCC(1,k)×Cmare designed, and some properties of HSCC(1,k)×K2and HSCC(1,k)×Cmare further studied.

HSCC(1,k); Hamilton graph; Cartesian product; Perfect matching

TN393

A

10.3969/j.issn.1003-6970.2018.07.015

师海忠(1962-)，男，博士，教授，互连网络设计与分析、有（无）向图语言、随机图语言、（V，R）-语言，（V，R）-半群，网络科学与语言等；陈璐璐(1993-)，女，硕士研究生，主要研究方向：网络科学与语言。

本文著录格式：师海忠，陈璐璐. k 次Herschel— 师连通圈网络[J]. 软件，2018，39（7）：72—78