求阴影部分面积的七种方法
2018-08-11胡尊岩
文/于 涛 胡尊岩

求阴影部分的面积是常见题型.对于不同的面积问题,要选择与它相适应的解法,才能减少计算量,快速求解.请看下面的例题.
一、直接利用公式法
例1同学们在学校小花园的一角种植了M,P,Q三种花,其所占的种植区域如图1所示,∠AOE=90°,AB=OB,CB∥OE,AB=4m,则种植M花的面积为( )

解析:∵∠AOE=90°,CB∥OE,∴CB⊥OA,
∵AB=OB,AB=4m,
∴OC=OA=8m,∠AOC=60°,∴∠COE=30°,
∴种植M花的面积为选A.
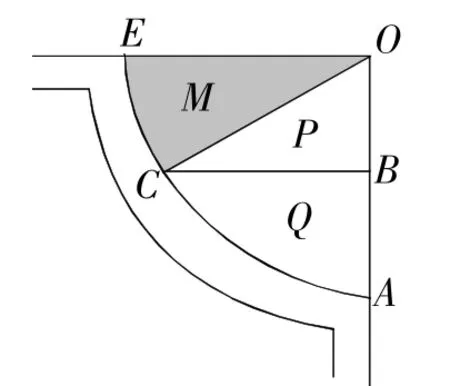
图1
二、等面积转化法
例 2 如图2,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8,则图中阴影部分的面积是( )

解析:连接OE,OF,OC,OD,过O作OM⊥EF于M,反向延长线交CD于N,如图3.
∵AB∥CD∥EF,∴S△ACD=S△OCD,S△AEF=S△OEF,
所以阴影部分面积等于扇形COD与扇形EOF的和,
∵AB=10,CD=6,EF=8,MO⊥EF,ON⊥CD,

图2
∴OD=OF=5,FM=ON=4,OM=DN=3,
∴△OFM≌△DON,
∴∠FOM+∠DON=90°,
∴∠EOF+∠COD=180°,
即S阴影=.选A.

图3
三、对称转化法
例3如图4,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数的图象上,求图中阴影部分的面积(结果保留π).
解析:根据双曲线的中心对称性,图中阴影部分面积的和是一个圆的面积.
由于⊙A与x轴和y轴相切,且圆心在双曲线上,

图4
设圆的半径为r,则点A(r,r)在双曲线上,
所以有r2=1,即r=1,所以圆的面积是π,
故图中阴影部分的面积是π.
四、平移法
例4如图5,已知两个半圆中长为4的弦AB与直径CD平行,且与小半圆相切,求图中阴影部分的面积.
解析:移动小半圆至与大半圆的圆心重合的位置,则阴影部分的面积不变,如图6.
设切点为H,连接OH,OB,

图5
又AB切小半圆于点H,故OH⊥AB,
故OB2-OH2=BH2=4,

图6
五、和差法
例 5 如图7,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD的延长线与AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
证明:(1)连接AD,OD,如图7.
∵AB为直径,∴∠ADB=90°,∴AD⊥BC,
∵AC=AB,∴点D为线段BC的中点.
∵点O为AB的中点,∴OD为△BAC的中位线,∴OD∥AC,
∵DF⊥AC,∴OD⊥DF,∴DF是⊙O的切线.
∵AC=AB,∴△ABC为等边三角形,∴AB=4.
∵OD∥AC,∴∠DOG=∠BAC=60°,
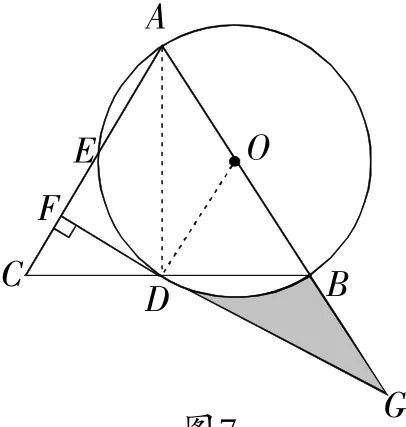
图7
六、重叠法
例6如图8,半圆O的直径AB=20,将半圆O绕点B顺时针旋转45°得到半圆O′,与AB交于点P.
(1)求AP的长;
(2)求图中阴影部分的面积(结果保留π).
解析:∵∠OBA′=45°,O′P=O′B,
∴△O′PB是等腰直角三角形,
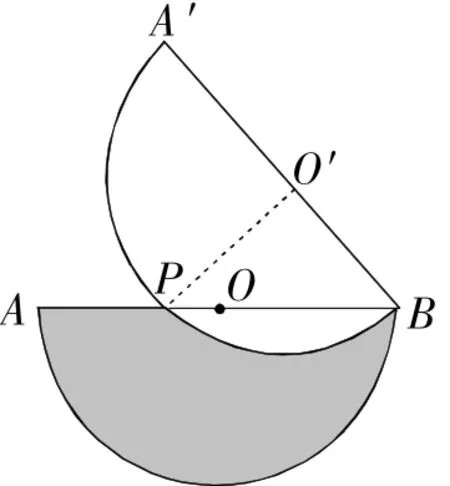
图8
七、整体法
例7如图9,分别以n边形的顶点为圆心,以1cm为半径画圆,当n=2018时,求图中阴影部分的面积之和.
解析:每个阴影的面积是以这个多边形的外角为圆心角的扇形面积,因多边形的外角和为360°,故可以求出阴影部分的面积和.
∵多边形的外角和为360°,
∴S1+S2+…+S2018=S圆=π×12=π(cm2).
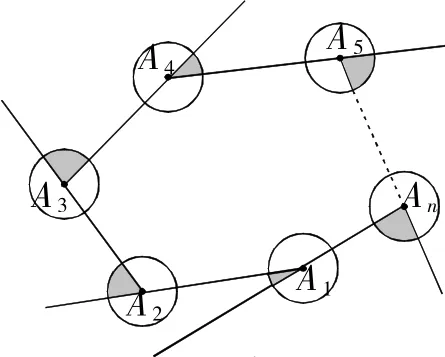
图9
