SOLO分层理论在培养初中生抽象拓展思维的应用举例*

2018-08-11广东省湛江一中培才学校524037李雪迎

中学数学研究(广东) 2018年14期

广东省湛江一中培才学校(524037) 李雪迎

1 问题的提出

在长期的初中数学教学实践中发现,由于受到升学压力、课时紧张、业绩评定等诸多方面的影响,较多的教育者更倾向于试题正确答案的讲解、应试经验的传授,却缺少对典型例题的详细解读;搞“题山题海”战术,而不注重学科知识的系统化整理,从而错过了培养学生抽象拓展思维能力的黄金时期.

而缺少相关引导、训练的学习者在学习中不注重知识的生成过程、推理论证、脉络关联,却热衷于死记硬背公式、结论、定理.SOLO分层理论的创始人比格斯(Biggs)教授所做的大量研究表明,那些喜欢熟记事实细节并使用机械学习策略的学生在传统的测试中获得了高分,但他们却获得了很低的SOLO等级.机械式学习导致学习者抽象拓展思维的缺失,不仅没法达到学习深度的要求,还严重挫伤了学习者对数学的学习兴趣.

2 SOLO分层理论在培养学习者抽象拓展思维的应用举例

现从中考复习课阶段的知识串讲作为一个示例,帮助学习者发现数学学科本身的规律性、一体性、趣味性,引导学习者发展抽象拓展思维.

2.1 “整式的乘法”中知二求二

对于正实数x,y,对于以下式子标记如下:

①(x+y)2,②(x−y)2,③x2+y2,④xy.

根据整式的乘法运算法则得:

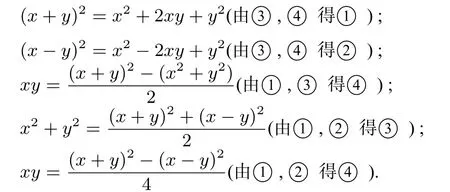
反思:根据和与差的完全平方公式中对应项系数相同(反)的数量关系,通过相加、减可以实现代数式(x+y)2,(x−y)2,x2+y2,xy之间的互相推导.

2.2 “相交线与平行线”中的知二得一

题设:如图1,已知AB//CD,CE为∠BCD的平分线交AB于E.结论:BC=BE.(证明过程:略)

在题设和结论中,共有三个信息:①AB//CD,②CE为∠BCD的平分线,③BC=BE.

反思:此处是借以①②为条件,得到结论③(①+②=＞③).而事实上,此处的三个信息可以任选两个进行组合,推导得到第三个信息.例如:①+③=＞②;②+③=＞①.实现了借助线段之间的位置关系、角之间的数量关系,得到了另外两条线段之间的数量关系.

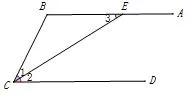
图1

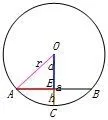
图2

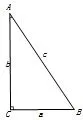
图3

2.3 “垂径定理”的应用:用于证明的“知二推三”和用于计算线段长的“知二求二”

如图2,在⊙O中,OC是半径,AB为弦,当OC⊥AB于点E时,记半径OA的长为r,弦AB的长为a,弦心距OE的长为d,拱高CE的长为h.

圆中常见四条线段的长度,知二求二:

①1已知r,d,得

②已知h,a,则d=r−h,在Rt△AEO中,d2=即解这个关于r的一元一次方程,得

反思:在定理中,由过圆心的线和弦之间位置关系得到线段、弧之间的数量关系.而根据圆的轴对称性质,可以由其中任意两条信息作为已知条件推导得到另外三个.

2.4 解直角三角形的应用:知二求二

如图3,在Rt△ABC中,∠C=90°,解这个直角三角形.

①应用勾股定理:若已知a,b,c中任意两条边,可以求出第三条边,此时由a,b⇒c;

②应用锐角三角函数:可以由两条边长度的比值(例:若已知a,b,求出先求出对应角的三角函数值(即再由三角函数值反过来确定角的度数(可求出∠B),此时由a,b⇒∠B;亦可由a,∠B⇒b.

反思比较:①中的已知两边求第三边,②中已知两边求内角,已知一边一角求边长.在解直角三角形,除了直角以外的五个元素(锐角1,锐角2,直角边1,直角边2,斜边)知二求三.

数学的学习是一个由特殊到一般,先猜想再到精准验证的过程.由三角形的三边关系(不等关系:两边之和大于第三边),到直角三角形条件下的等量关系(勾股定理),而锐角三角函数则在勾股定理的基础上得到了边角之间的互推关系,锐角三角函数不仅使用起来简便,更是勾股定理的延伸和补充.

2.5 总结

以上示例,虽然来自不同知识角度,但也能发现它们的互通之处:代数几何不分家、“数形结合”的主线贯穿整个初中数学教学.教育者可以结合数学学科特点,引导学生将各类型知识串联,通过类比对比,不仅能增强学习者的对数学的学习兴趣,还对知识理解的更透彻,更能促进学习者形成抽象拓展的思考方式.

3 SOLO理论在培养学习者抽象拓展思维过程中应注意的几个方面

3.1 营造民主课堂、鼓励学生参与

在教学中,有较多教师习惯于“满堂灌”,学生在课堂上只是个勤快的“搬运工”.在如此“乖乖听课”的学生面前,教学任务表面上可以轻松完成,但整个课堂没有学生积极参与、质疑、讨论、评价、反馈,缺乏民主和活力,拓展抽象思维的培养就是空话.

《义务教育数学课程标准》(2011年版)将“数学学习”和“数学教学”合为“教学活动”.“数学活动”是师生积极参与、交往互动、共同发展的过程,有效的教学活动应是“学”与“教”的完美统一,学生是学习的主体,而教师是学习的组织者、引导者与合作者.教师要想办法营造轻松、民主的课堂,让学生乐于参与到课堂,为学生创设有利于抽象思维发展的环境,鼓励学生去发现问题、解决问题.

3.2 注重一题多解、归纳总结

抽象拓展思维的培养需要学习者从不同的角度去考虑问题,而解题教学中的一题多解可以引导学生对同一问题进行多方位思考、探求不同的思维方式.而来自同龄人的思维方式,更易被接受也更能促进学习者的学习动力.对于经典题型的一题多解,教育者需要及时将各种解法类比、对比,从思考角度(我们最容易想到的)、解题方式(运用的知识点)、计算量大小(过程的繁易程度)等方面进行归纳总结,帮助学生把所学的知识系统化,提高学生思维的灵活性、多向性、深刻性、缜密性,激发学生思维的发散性和概括性,从而促进他们抽象拓展思维的全面发展和提高.