随机网络队列队长过程非负下鞅的构造

樊亚云，冯晶晶，邢瑞芳

(西安培华学院 智能科学与信息工程学院， 西安 710125)

鞅论[1-4]是概率论中的一个独立分支,是概率论与随机过程等方面的基础。近年来,鞅方法已成为研究随机网络队列的一个重要工具。本文在对具有马尔可夫到达无限等待空间的多服务台随机流体网络队列高负荷极限基础上，将鞅方法[5-7]引入随机流体网络队列中，在鞅的角度上来分析网络队列的网输入过程的高负荷极限。

1 主要方法

通过研究计数过程的相关鞅及其性质来证明模型的高负荷极限，首先给出非负下鞅的Doob-meyer分解定理。

定理1[8]如果Y是一个具有非负样本路径的下鞅，对每个t，E[Y(t)]<∞，而Y适应过滤F≡{Ft}，存在F-可料过程A，称为Y的补集或对偶可料，A具有非负非降的样本路径，对每个t都有E[A(t)]<∞，M≡Y-A为一个F-鞅，其中A是唯一的。

极限过程的鞅为其补偿计数过程。定义一个随机过程N≡{N(t):t≥0}，在D中有非降非负积分值的样本路径，且N(0)=0，随机过程样本路径完全连续(在一定的规则下)，同时Lebesgue可测，因此补集A可以表示为一个积分；

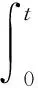
其中X≡{X(t):t≥0}是适应F-过滤的,当补集具有这样的积分表示时,X是计数过程N的随机密度。

引理1[8]如果N是一个非突变性单位跳跃计数过程，其满足一个滤波F，同时对所有的t，E[N(t)]<∞。如果N的补集由定理1提供，A为连续的，则鞅M≡N-A是个平方积分鞅,具有满足F平方变差过程：

〈M〉=A， [M]=N

2 模型及高负荷极限

研究具有k个服务台，每一个服务台都是具有无限等待空间的单一服务，外部到达的顾客在服务台进行服务，服务完成后按照一定的速率离去，每个服务台的顾客以马尔可夫的方式转移到另一个服务台或者直接离开流体网络,同时注意服务台在对队列的服务过程中有一定的服务干扰，当服务受到干扰，则服务停止，当干扰结束后服务继续，一直延伸到下一次干扰开始。

模型的基本随机元素指定如下：

A≡(A1,A2,…,Ak)表示在k个服务台的随机输入过程(到达过程)；

S≡(S1,S2,…,Sj)在第一个忙时单元中j服务台服务完人数的累积(服务过程)；

r≡(r1,r2,…,rk)表示k个服务台确定性的输出率(服务完成)；

R≡R(i,j)表示队列中第i个服务台服务完转移到第j个服务台人数的累积(总转移人数)；

顾客的路径用示性向量来决定；{χi, j(n):n≥1}，1≤i≤k和1≤j≤k，

χi, j(n)=1表示第n个顾客从第i个队列中服务完转移到j队列；

χi, j(n)=0，表示第n个顾客在第i队列进行服务完后离开网络。

对每一对(i,j)，使

(1)

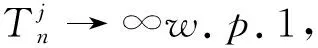
Ij≡{Ij:1≤j≤k}

其中Ij≡{Ij(t):t≥0}。如果第j服务为无干扰的则有Ij(t)=1；相反，如果第j服务为有干扰的则有Ij(t)=0。

定义Uj(t)和Dj(t)表示累积的无干扰时间及累积的有干扰时间。定义：

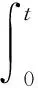
(3)

Dj(t)≡t-Uj(t)，t≥0

(4)

Bj(t)表示第j个服务台在[0,t]时刻内的累积忙时，第j个服务台累积闲时过程为

Yj(t)≡Uj(t)-Bj(t),t≥0

(5)

则有：

Bj(t)+Yj(t)+Dj(t)=t,t≥0

(6)

定义队长过程：

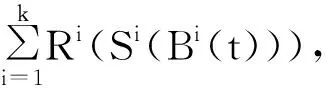
忙时过程定义为：

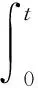
(8)

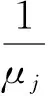
并且：

Xj(t)≡Zj(0)+ξj(t)+ηj(t)

(11)

diag(μ)为K×K阶对角矩阵。

定理2(反射映射的表示)[8]对所有的非负向量λ,μ∈Rk，以及所有的非负K×K阶矩阵P≡(Pi, j)，具有Pt≡Q∈Η，

Z=φ(X)，φ(X)=diag(μ)Y

(12)

其中:Z由式(7)定义；X由式(11)定义；Y由式(5)定义；(φ,φ)为反射映射；相关的列随机矩阵Q≡Pt。有：

或者等价

Z=X+(I-Q)diag(μ)Y

(14)

以及：

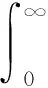
(15)

3 主要结果

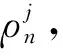
Zn≡Zn(t)≡n-HZn(nt)，t≥0

(16)

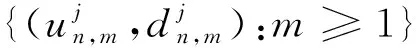
定义Nj≡{Nj(t):t≥0}为无干扰时间的计数过程，

Dj为随机和，表示的是所有干扰时间和：

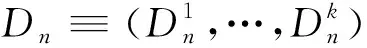
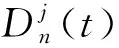
引进用于刻画模型的主要极限定理的一系列的D中的随机向量，使得：

An(t)≡n-H(An(nt)-λnnt)，t≥0

Sn(t)≡n-H(Sn(nt)-μnnt)，t≥0

Rn(t)≡n-H(Rn(nt)-Pnnt)，t≥0

(21)

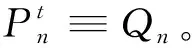
Zn的收敛相关刻画为；

Yn(t)≡n-HYn(nt)

(22)

Bn(t)≡n-H(Bn(nt)-nt)，t≥0

(23)

定理3(具有服务干扰的高负荷极限) 假设

(An,Sn,Rn,Dn,Zn(0))⟹(A,S,R,D,Z(0))，n→∞

(24)

所在的空间为D([0,∞),Rk2+3k,WM1)×Rk，其中：(An,Sn,Rn)由式(21)定义；Dn由式(20)定义；Zn由式(16)定义。具有0≤H<1，

P((A,S,R,D)∈D1)=1

(25)

另外，如果在Rk中存在向量λ和μ和矩阵P，Pt∈Η，在Η中

以及

在D([0,∞),R3k,WM1)则有：

(Zn,Yn,Bn)⟹(Z,Y,B)

(28)

其中：

证明

考虑对所有的服务台都是忙碌状态的情形，用n-H来刻画随机过程，使得：

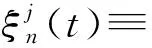
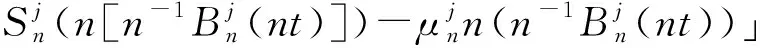
(30)

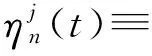
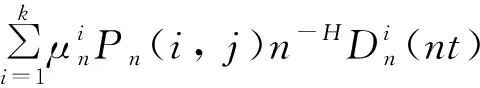
(31)

并且：

鞅方法构造：构建出一个具有合适过滤(自然σ-域)的下鞅，再减去它的可料过程补集，利用引理1构造出M=[M]-〈M〉为一个鞅，[M]是M的补集。

下面的过程将被证明是F-鞅：

(33)

要求MA、MS都为平方可积鞅，满足滤波F≡{Ft:t≥0}，

Ft≡σ(Z(0),An(s),Sμ,k(s),k≥1, 0≤s≤t)t≥0

(34)

要提供上述过程的理论支持，首先要证明下面的引理，其为构造鞅刻画的条件。

引理2 如果E[X(0)]<∞，在适应滤波式(34)下，随机过程Y定义如下：

(35)

其具有跳跃的计数过程，因此对所有的t≥0，有E[Y(t)]<∞。

证明

应用不等式性质可得：

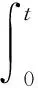
两边同时求和：

然后：

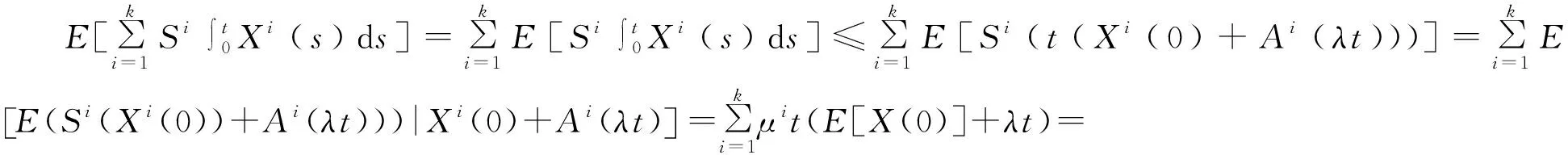
证明完毕。

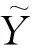
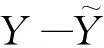
证明应用积分定理[10]，在鞅的基础上考虑有界可料过程的积分，即定义鞅的积分有界变差过程

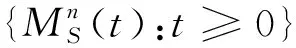
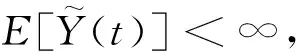
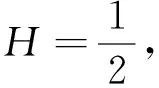
则有：

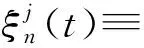
其中：

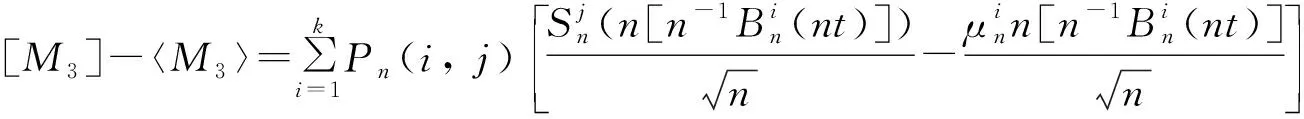
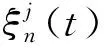
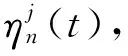
其中cn为式(27)的高负荷极限。

Xn=Zn(0)+ξn+ηn

(40)

Zn=φQn(Xn)

Yn=diag(μn)φQn(Xn)

(41)

以及：

Bn=-Yn-Dn

(42)

因为在C中子函数都是非负严格递增的，利用复合映射外加条件在D([0,∞),Rk,SM1)中Xn→X，然后对式(38)～(42)再利用文献[8]定理13.2.3、定理14.5.5[8]可得：

证明完毕。