异构分布式系统中实时可任意切分任务调度算法
2018-08-10仝武宁刘道华李宏斌
仝武宁, 刘道华, 李宏斌
(1. 陕西中医药大学 基础医学院, 陕西 咸阳 712046;2. 信阳师范学院 计算机与信息技术学院, 河南 信阳 464000)
0 引言
可分任务是一种可被切分成任意多个子任务的任务,且被切分成的子任务之间没有依赖关系,可以在许多不同的处理机上同时处理.大量的文献对可分任务进行了研究,且可分任务理论已经被成功地应用于许多科学问题中,如:图像处理、信号处理以及文本搜索等应用领域[1-3].在分布式系统中,任务调度策略的优劣直接影响系统的性能,设计较优的调度策略以提高系统的效率、用户满意度等是分布式系统中任务调度研究的主要目标.文献[4]提出一种利用可分任务理论计算满足实时可分任务完成截止时间约束时所需最少处理机的方法;文献[5]提出了一种考虑处理器可用时间的实时可分任务调度算法.文献[6]对文献[5]中提出的算法进行了改进,得到了调度问题的精确解.文献[7]将实施可分任务划分成紧急任务和非紧急任务,然后根据不同的任务类型设计了不同的调度方案,以达到最大化接受率的目的.文献[8]考虑任务对系统的最低需求,设计了一个考虑资源可用性的任务调度算法以提高资源的利用率.也有越来越多的文献对实时可分任务进行了研究[9,10],然而在已有的研究文献中,都旨在最优化资源利用率等单一目标,并没有考虑优化多个目标的资源调度.因此,本文针对异构分布式环境下的实时可分任务调度问题进行了研究,为最大化服务收益、任务接受率以及最小化完成时间设计了有效的算法.
1 问题描述
本文采用星型网络拓扑,即系统中包含有一个主处理机P0和N个从处理机P1,P2,…,PN.主处理机P0负责判断是否接收用户提交的任务以及将接受的任务分发给从处理机,P0和从处理机Pi(i=1,2,…,N)之间有进行通信的链路li,且通过通信链路li传递一个单位任务量所需要的时间为gi.从处理机Pi(i=1,2,…,N)负责接收和处理主处理机分配给它的任务,且该处理机处理一个单位任务量所需要的时间为wi.
本文研究的对象是可分任务,即任务可以被无限拆分,拆分后的子任务之间没有任何依赖关系.对于任务Τj,用三元组来表示,即Τj=(aj,dj,αj),其中aj和αj分别表示任务Τj的到达时间和任务量,dj是任务Τj相对完成截止时间,则任务Τj的绝对完成截止时间为aj+αj.用户提交任务后,分布式系统可以根据用户的任务量,任务的完成截止时间来确定任务的服务收益,用δj表示任务Τj的服务收益.
异构分布式系统中具有完成截止时间的实时可分任务调度问题可以归结为:当任务到来时,主处理机如何根据当前从处理机的状态决定是否接受该任务,以使得一段时间内服务收益和任务接受率最大;当用户提交的任务被接受时,如何将该任务分配到不同的处理机上以使得任务的完成时间最短.因此,要解决该问题需要解决三个子问题:1)主处理机如何判断用户提交的任务是否可以被接受?2)任务被接受后,如果处理机处于忙的状态,需要将接受的任务置于任务等待队列中,如何确定任务等待队列中任务的顺序,以使得尽可能多的任务按时完成?3)任务按照何种策略被分配到处理机上以使得任务完成时间最短?
2 考虑服务收益的实时可分任务调度算法
2.1 任务接受规则与任务删除策略
当用户提交任务后,主处理机要根据从处理机的状态以及任务等待队列中的任务量来确定是否接受该任务,本文提出了一种同时考虑任务完成时间和任务的服务收益的策略以确定该任务是否被接受.当用户提交的任务Τj同时满足式(1)和式(2)时,该任务被拒绝,否则就接受该任务.
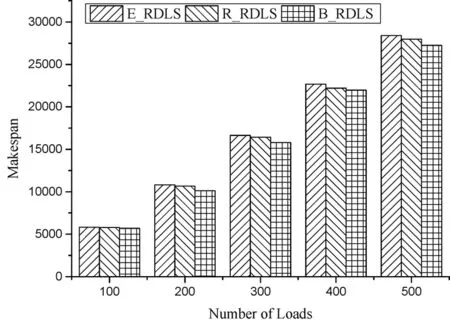
aj+dj (1) (2) 其中sj,tj和Q分别是任务Τj的预计开始时间、预计执行时间和当前的任务等待队列.任务Τj的预计开始时间由式(3)计算得到,本文采用改进的文献[11]提出的方法计算任务的预计执行时间,如式(4)所示. (3) (4) 当任务Τj被接受且满足aj+dj ηj=(sj+tj)-(aj+dj), (5) tQ={Τk|tk>ηj,Τk∈Q}, (6) (7) 当处理机都处于忙的状态时,未进行处理的任务就加入到任务等待队列中.任务的执行顺序会影响任务的完成时间、任务的接受率等,因此本文提出了一种综合考虑任务完成时间和服务收益是排序策略,即通过式(8)计算任务等待队列中任务的θj(j=1,2,…),对任务等待队列中任务按照θj(j=1,2,…,)值由小到大的顺序进行排序. (8) 其中0≤μ,ν≤1是两个权重系数,且有μ+ν=1.经过大量仿真实验发现,当μ∈[0.58 0.67]时仿真结果更优,因此在实验中μ取0.6. 当有处理机空闲时就要取任务等待队列中的任务分配给空闲的处理机以进行处理,如何有效地将任务分配到不同的处理机上以使任务的处理时间最短是需要解决的关键问题.式(9)给出了一个以最小化任务完成时间为目标的优化模型. (9) (10) (11) (12) 算法1 任务调度算法框架 输入:任务Τj,任务等待队列Q; 输出:任务Τj的调度方案; If 任务Τj同时满足式(1)和式(2) do 任务Τj被拒绝; else If 任务Τj满足式(1),不满足式(2) do If 任务等待队列Q为空 do 任务Τj被拒绝; else 根据式(5)—(7)确定要从任务等待队列Q中删除的任务;通过式(8)计算任务Τj的θj值,并将任务Τj插入到Q中; end else 通过式(8)计算任务Τj的θj值,并将任务Τi插入到Q中; end 取出任务等待队列Q中的第一个任务,表示为Τj′,根据(10)—(12)将Τj′分配到处理机上; end. 为评价算法的有效性,采用三种评价指标,分别为:接受率、服务收益率和任务完成时间,且三个指标的定义如下: 接受率:一段时间内接受任务的任务量与用户提交任务的任务量的比值,即 (13) 其中Ω和Nr分别是接受任务的集合和一段时间内用户提交任务的个数. 服务收益率:一段时间内接受任务的服务收益与用户提交任务的服务收益的比值,即 (14) 任务完成时间:执行完所有任务所需要的时间,即所有处理机结束执行的时刻,定义为: (15) 其中Ti是处理机Pi(1≤i≤N)结束执行任务的时刻. 为验证算法的有效性,进行了3组对比实验,每组实验中有两个对比算法,第一个对比算法是文献[7]提出的算法,表示为E_RDLS,另一个是文献[8]提出的R_RDLS算法,本文提出的算法表示为B_RDLS. 图1给出了系数R变化时得到的任务接受率,图2给出了系数R变化时得到的任务服务收益率,图3给出了不同任务数量时得到的任务完成时间. 图1 任务接受率随R的变化情况Fig. 1 Acceptance ratio v.s. R 图2 服务收益率随R的变化情况Fig. 2 Benefit ratio v.s. R 图3 任务完成时间Fig. 3 Makespan of Loads 图1给出了任务接受率随系数R变化的情况,显然本文提出的B_RDLS算法在相同系数R的情况下得到比对比算法较高的接受率.当任务具有小的相对完成截止时间和大的任务量时,该任务就具有较大的服务收益,被接受的可能性就大,从而使得算法具有较高的接受率.当任务具有大的相对完成截止时间时,该任务被接受的可能性就大,因此也能提高算法的接受率. 由图2中任务服务收益率随系数R变化的情况可以得到:本文提出的B_RDLS算法在相同系数R的情况下得到比对比算法要高的服务收益率.服务收益大的任务容易被接受,当该任务不能按时完成时,采用从任务等待队列中删除任务的策略(删除任务等待序列中服务收益较小且能够使得当前被接受的任务按时完成的任务),以尽可能地接受服务收益较高的任务,因此本文提出的算法在不同R的情况下可以得到比对比算法较高的服务收益率. 图3给出了任务量由100到500变化时任务的完成时间变化情况.由图3可以看出B_RDLS能够得到比E_RDLS和R_RDLS算法更小的任务完成时间.优先选择处理速度快的处理机进行任务分配可以使得任务的完成时间减少.此外,设计的方法可以自动确定给不同处理机分配的任务量以实现处理机的无间隙处理任务,同样可以减少不必要的时间消耗,因此本文的B_RDLS算法可以得到较小的任务完成时间. 研究了异构分布式系统中考虑服务收益的实时可分任务调度问题,设计了最大化任务服务收益的任务接受/拒绝规则以及从任务等待队列中删除任务的策略,以使得所有接受的任务能按时完成的同时,提高服务收益和任务接受率.为减小任务的完成时间,设计了综合考虑任务服务收益和任务相对完成截止时间的排序策略、自适应地为处理机分配任务,使处理机无间隙地处理任务等方案,以减少任务的执行时间.仿真实验结果表明,设计的算法能够得到比对比算法较高的任务接受率、服务收益率以及较小的任务完成时间.然而,算法中任务的排序策略中两个参数会影响算法的性能,任务的不同,最优的参数设置也不同.因此,如何只适应地确定出两个参数的值或者给出更优的任务排序策略是需要进一步研究的工作.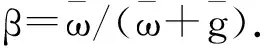
2.2 考虑服务收益的排序策略
2.3 任务调度模型及算法

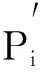
3 实验与分析
3.1 参数设置

3.2 评价指标
3.3 对比算法与实验结果


3.4 实验分析
4 结语
