一类具有目标收益导向的淡水生态系统生产者-消费者管理模型
2018-08-10刘开源
刘开源 ,高 斯
(1.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007;2.新密市长乐路初级中学,河南 新密 452370)
0 引言
渔业是以水生生物资源为生产物质基础、以水域为生产作业场所的资源型基础产业.渔业资源(包括水产动物和植物)是可再生的生物资源,是自然资源和人类食物的重要来源之一,其中鱼类等渔业资源为人们提供了约40%的动物蛋白质[1].这些生物资源的可持续生产以及产品质量的提高,均依赖于水体的质量.但近年来,工业、农业、畜牧业及旅游业的发展,大量的富营养物质(如氮、磷)进入水体,使得江河湖泊等淡水水体富营养化程度不断提高,促使水体内藻类等生产者大量繁殖(甚至发生水华),导致水体透明度和溶解氧含量降低,进而使得水体内浮游动物和鱼类等消费者的生存环境恶化[2,3],影响水体生态系统的健康发展,从而制约渔业资源的开发和利用.
控制水体富营养化所引发的藻类水华是当今世界性难题.据统计,中国富营养化和超富营养化湖泊分别已达到湖泊总量的66%和22%[4].近年来,国内外学者从生态工程技术、化学治理、生物治理等方面提出了富营养化水体的治理措施,这些措施各有利弊.生物治理主要包括经典的生物操纵和非经典的生物操纵理论[5],利用鲢鱼等滤食性鱼类消费者直接滤食藻类属于非经典生物操纵理论.因为生物治理利用水生动植物组合方式对富营养化水体的净化进行调控,且不会产生二次污染,同时又能获得一定的渔业生物资源,因此生物治理被认为是水生态环境最理想的治理措施.
已有不少文献研究了水体生产者(藻类等)和消费者(鱼类等)的相互作用模型并取得了丰富的成果[6-9].在实践中,某一水体的管理者和经营者在治理和维持良好水生态系统的同时,还希望对水体中的水生动植物等具有经济价值的水产品进行开发,获得一定的经济效益.本文借鉴“养鱼先养水”的可持续发展理念,考虑水体生态系统中物质-生产者-消费者的相互作用关系,同时考虑经营者的目标收益,利用微分代数系统[10,11],建立一类具有目标收益导向的水生生产者-消费者管理模型并进行研究.
1 模型建立
假设某一水体生态系统由营养物质(氮、磷等)、浮游植物生产者、浮游动物及鱼类消费者组成.将营养物质的浓度、生产者和消费者的密度分别记为N、x、y,并假设生产者对营养物质的摄取满足Michaelis-Menten-Monod函数,消费者对生产者的捕食率满足Holling II功能性反应函数,从而有下面的模型:
(1)
本模型中所有的参数均为非负,N0为营养物质的初始浓度;D为流入速率;m1,m2分别为生产者对营养物质、消费者对生产者的最大吸收率;k1,k2分别为半饱和常数;θ1,θ2分别代表生产者x和消费者y死亡并被分解的营养物质的循环率(0<θ1,θ2<1);d1、d2代表浮游植物x和浮游动物的死亡率(0 为方便起见,记 θ1d1x+θ2d2y, f(z,E,S)=(f1(z,E,S),f2(z,E,S),f3(z,E,S)), g(z,E,s)=(px-c)E-s. 这里z=(N,x,y),s是一个分支系数.本文主要讨论系统(1)正平衡态的存在性及稳定性. 系统(1)的正平衡态可由下面方程组计算得到: 经过计算,有下面的结论: 定理1 若βm2>d2, 则系统(1)存在正平衡点M*(N*,x*,y*,E*),其中: A=Dm2(βm2-d2), B=-((DN0-Dk1)(βm2-d2)m2+ (θ1d1-m1)d2k2m2+ k2θ2d2βm2(αm1-d1-E*)), C=-(DN0k1m2(βm2-d2)+d2k1k2θ1d1m2- (d1+E*)k1k2βm2θ2d2), 对于正平衡态M*(N*,x*,y*,E*)的稳定性,有下面的定理: 定理2 若a11a22>a12a21+a23a32且 则系统(1)正平衡点M*(N*,x*,y*,E*)是局部渐近稳定的(其中a11,a12,a21,a22,a23,a32如式(6)所定义). 证明令χ=(N*,x*,y*,E*),取 χT=QMT, 其中: 则 (3) 进而系统(1)可化为 (4) 为了讨论系统(1)正平衡态的稳定性,首先对系统(4)进行局部参数化[10,11].取 其中: h:R3→R4是光滑映射,那么,关于系统(4)的参数系统如下[13]: (5) 可得矩阵 其中: (6) 经计算可得矩阵E(M*)的特征方程为: λ3+b1λ2+b2λ+b3=0, (7) 其中: b1=-(a11+a22+a33)= b2=a11a22+a3(a11+a22)- a12a21-a32a23-a13a31= b3=-a11a22a33+a12a21a33+ a11a32a23+a13a22a31= 可以验证, b1=-(a11+a22)>0, b2=a11a22-a12a21-a23a32>0, b3=a11a23a32-a13a21a32= 因为0<α<1,0<β<1,0<θ1<1,0<θ2<1,所以b3>0.由于 b1b2-b3=-(a11+a22)(a11a22-a12a21- a23a32)-(a11a23a32-a13a21a32)>0, 由Routh-Hurwitz判据可得,特征方程(7)的特征根均小于0,从而正平衡点M*(N*,x*,y*,E*)是局部渐近稳定的.证毕. 下面将目标收益s作为分支参数,讨论系统(1)的Hopf分支情况. 定理3 如果存在s*使得当s=s*时 b1b2-b3=0, 那么当 时,系统(1)在s=s*处产生Hopf分支. 证明如果存在s*使得当s=s*时b1b2-b3=0,则特征方程(7)可化为 (λ2+b2)(λ+b1)=0, (8) 其特征根为 若系统在s=s*处产生Hopf分支,则其具有零实部的复特征根成对出现,记 λ1=p(s)+iq(s), λ2=p(s)-iq(s), λ3=-b(s). 将其代入方程(8),计算得[12] A(s)p′(s)-B(s)q′(s)+C(s)=0, B(s)p′(s)+A(s)q′(s)+D(s)=0, 其中: A(s)=3p2(s)+2b1(s)p(s)+b2(s)-3q2(s), B(s)=6p(s)q(s)+2b1(s)q(s), A(s*)=-b2(s*), 从而可得 由定理条件可知, 因此,当s 将浮游植物生产者作为渔业开发对象,考虑到管理者的目标收益,建立并描述了物质-生产者-消费者的微分代数系统(1),讨论了系统正平衡态的存在性、渐近稳定性及Hopf分支.如果把目标收益s作为分支参数,那么存在一个临界阈值s*,当人们设定的目标收益s小于s*时,系统的正平衡态是渐近稳定的,此时水生态系统中的各资源可以达到稳态共存;如果目标收益期望值过大(s>s*),则系统中各物种将会出现周期震荡.限于篇幅,本文只对正平衡点及Hopf分支的存在性进行了讨论,其他动力学性质如周期解和极限环的个数、稳定性等的研究将是下一步的工作.2 平衡态稳定性的分析


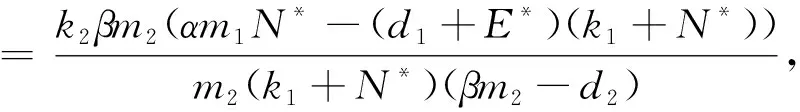



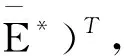


3 Hopf分支

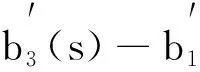
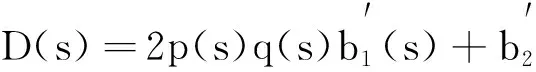
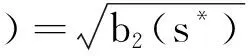


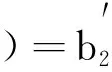
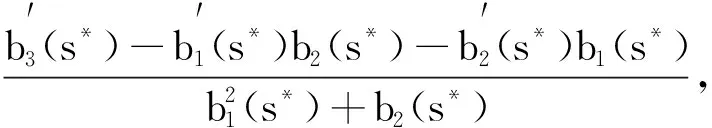
4 结语
