一类时滞虫媒传染病模型的稳定性分析
2018-08-10何俊杰
王 娟,何俊杰
(信阳师范学院 数学与统计学院,河南 信阳 464000)
0 引言
目前出现的传染病的种类有很多,按传播途径分类,可以分为消化道传染病、呼吸道传染病、虫媒传染病和动物源性传染病.其中,虫媒传染病是由病媒生物传播的自然疫源性疾病,常见的有流行性乙型脑炎、鼠疫、莱姆病、疟疾、登革热等危害性较强的传染病.
传染病动力学是利用数学模型定量讨论传染病流行规律的理论性研究方法.通过建立数学模型模拟疾病的发展规律,可以为预测疾病的变化趋势、分析疾病的流行原因、寻找预防和控制疾病传播的有效策略等提供理论依据.1997年,FENG等[1]建立了一个媒介与寄主模型研究登革热.2004年,FENG等[2]和CHATTOPADHYAY等[3]分别建立动力学模型,利用奇异摄动技术和统计回归分析研究了遗传因素和社会环境对疟疾传播的影响.2005年,TUMWIINE等[4]建立了一个带蚊虫发育延迟的数学模型,用来研究蚊虫控制对疟疾传播的影响.CRUZ-PACHECO等[5]建立并研究了虫媒(蚊子)与鸟类之间传播西尼罗河热(West Nile virus)的模型.近年来,很多学者还考虑了疾病复发、复杂网络、脉冲控制和离散时滞等对媒介传染病的传播的影响[6-9].
本文考虑易感人类受到带病虫媒叮咬后疾病具有潜伏期的情况,建立了一类时滞微分方程模型来描述带有非线性发生率和接种疫苗的虫媒传染病的传播规律.
1 模型的建立
本文把传染病流行地区的人类分为三种:易感类、染病类、康复类,分别用S(t)、I(t)、R(t)表示t时刻这三类人口的数量.因为虫媒(如蚊子)的寿命短且无法得到治疗,所以可以假设虫媒(如蚊子)被感染后无法康复.于是虫媒只有两类:易感类和染病类,分别用M(t)和V(t)表示t时刻易感和染病虫媒的数量.
记β1为易感人群被虫媒叮咬并被感染的概率,α表示媒介控制的概率(使用杀虫剂、蚊帐等).一个易感人类与染病媒介有效接触被感染的概率可表示为:
其中K为常数.易感虫媒的感染率采用双线性发生率,记β2为易感虫媒叮咬染病人类并被感染的概率,τ为易感人类被感染后潜伏期的长度.具体来说,易感人类在t时刻被虫媒叮咬并被感染,在t+τ时刻才具有传染性,由此易感虫媒与染病人类接触并被感染的概率为λ2=β2I(t-τ).
假设:
(1)各人群的自然死亡率都相等,设为μ1;各类媒介的自然死亡率也都相等,设为μ2;
(2)新出生(增加)的人类和媒介都是易感的,设单位时间内新增加的数量分别为b1,b2;
(3)假设接种疫苗可以获得对该传染病的完全免疫;
(4)疾病只在人和虫媒之间互相感染.
根据仓室建模原理,可以分别建立人类系统(1)和虫媒系统(2):
(1)
(2)
记人类人口总数和虫媒总数分别为
N1(t)=S(t)+R(t)+I(t),
N2(t)=M(t)+V(t),
对两式关于t求导,并将系统(1)代入,可得

容易验证
不失一般性,假设

于是系统(1)和系统(2)中,
进而只需要考虑非线性系统:
(3)

2 基本再生数与平衡点

则系统(3)等价于
其中X=(I,V,S)T.F,V的雅克比矩阵在无病平衡点X0=(0,0,S0)T处的值分别记为
其中
可以计算基本再生数:
(4)
设E*=(S*,I*,V*)∈Γ{E0}是系统(3)的正平衡点,代入系统(3)可解得
(5)
显然,当R0>1,即
时,系统(3)存在唯一的正平衡点,即地方病平衡点E*=(S*,I*,V*).
3 无病平衡点的稳定性
定理1 当R0<1时,系统(3)的无病平衡点E0是局部渐近稳定的;当R0>1时,无病平衡点E0是不稳定的.

J(E0)=

它具有3个特征根,其中λ1=-(φ+μ1)<0;λ2,λ3由方程
λ2+(μ1+γ+μ2)λ+μ2(μ1+γ)-
(6)
确定.方程(6)可整理成F(λ)=G(λ),其中
F(λ)=λ2+(μ1+γ+μ2)λ,
G(λ)=μ2(μ1+γ)·
一方面,连续函数F(λ)满足
F(0)=0,F(+)=+.

所以,函数F(λ)与函数G(λ)在(0,+)上一定相交,即方程(6)存在正实数解.所以无病平衡点E0不稳定.

-ω2+(μ1+γ+μ2)ωi+μ2(μ1+γ)-
分解实部和虚部,分别得到
两式平方和,消去cos(ωτ)和sin(ωτ),得
ω4+(2μ2(μ1+γ)+(μ1+γ+μ2)2)ω2+
(7)
记z=ω2,则方程(7)转化为一元二次方程:
z2+c1z+c2=0,
(8)
其中:
c1=2μ2(μ1+γ)+(μ1+γ+μ2)2>0,
显然,方程(8)没有正实根,进而不存在正实数ω使得z=ω2.

定理2 当R0≤1时,系统(3)的无病平衡点E0在Γ上是全局渐近稳定的.
证明构造函数
(μ1+φ)I(t)+

(9)
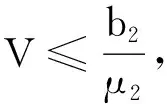
时,L(t)=0.L沿着系统(3)的解关于t的导数为
(μ1+φ)(μ1+γ)·
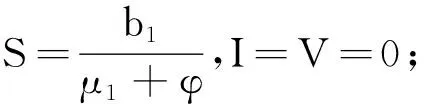
4 地方病平衡点的稳定性
系统(3)在地方病平衡点E*=(S*,I*,V*)处的特征方程可以写成
λ3+a1λ2+a2λ+a3=
e-(λ+μ2)τ(T1λ2+T2λ+T3),
(10)
其中
(φ+μ1)(μ1+γ+μ2)+μ2(μ1+γ)-
μ2(μ1+γ)(φ+μ1)-
T1=-β2I*,
当R0>1时,I*≠0,且(S*,I*,V*)满足
所以
进而,对任意的λ≥0,τ≥0,e-(λ+μ2)τ≤1,特征方程(10)的系数满足
a1>0,
(φ+μ1)(μ1+γ+μ2)+
(1-e-(λ+μ2)τ)μ2(μ1+γ)>0,
(1-e-(λ+μ2)τ)μ2(μ1+γ)(φ+μ1)>0,
T1<0,T2<0,T3<0,
所以方程(10)没有非负实根.
假设方程(10)存在纯虚数解λ=iω,ω>0,与定理1的证明过程类似,z=ω2需满足
z3+d1z2+d2z+d3=0,
(11)
其中,
(12)
显然,当d1≥0,d2≥0,d3>0时,方程(11)没有正实根,进而不存在正实数ω使得z=ω2,从而上面假设不成立,所以方程(10)不存在纯虚数解.

所以,可以得到如下定理:
定理3 当R0>1,d1≥0,d2≥0,d3>0时,系统(3)的地方病平衡点E*在Γ上对任意的时滞τ≥0都是局部渐近稳定的.
5 结语
本文建立和研究了一类具有非线性发生率的时滞虫媒传染病模型,其中人类感染疾病的疾病发生率采用饱和发生率,媒介采用双线型发生率.具体来说,首先讨论了无病平衡点与地方病平衡点的存在性与唯一性,并给出了基本再生数的具体表达式,然后分析了无病平衡点和地方病平衡点的稳定性.
