畜牧养殖环境监测自主移动平台轨迹跟踪控制算法

吕恩利，韦鉴峰，王 昱，赵俊宏，王飞仁，刘妍华



畜牧养殖环境监测自主移动平台轨迹跟踪控制算法

吕恩利1,2，韦鉴峰1，王 昱1,2，赵俊宏1，王飞仁1，刘妍华3※

（1. 华南农业大学工程学院，广州 510642；2. 华南农业大学南方农业机械与装备关键技术教育部重点实验室，广州 510642； 3. 华南农业大学工程基础教学与训练中心，广州 510642）

为实现畜牧养殖环境全方位监测，开发了可实现轨迹跟踪的自主移动监测平台。以具有非完整约束特性的自主移动平台为研究对象，研究其轨迹跟踪问题。在平台的结构基础上，通过建立其运动学模型及误差模型，提出基于Lyapunov函数和反推（Backstepping）时变状态反馈控制方法的轨迹跟踪算法，实现自主移动平台转向轮转角和行驶速度的控制。仿真和试验表明：所提出的控制算法能使该平台较好的收敛于期望轨迹，当跟踪期望轨迹稳定后，控制参数为(1,2,3,4)=(0.1,0.2,0.15,0.3)时，直线轨迹跟踪误差为x=±7 mm，y=±9.8 mm，=±4.2°，圆弧轨迹跟踪误差为x=±6.2 mm，y=±8.3 mm，=±5.8°，取得良好的跟踪精度。该研究可为畜牧养殖环境监测自主移动平台轨迹跟踪控制提供参考。

环境监测；算法；模型；自主移动平台；轨迹跟踪；运动学模型；Lyapunov函数；Beckstepping

0 引 言

准确高效地采集畜牧环境参数是反馈控制畜牧环境的基础[1]，随着产业自动化与智能化的发展，自动化与智能化装备代替人工劳动成为产业重要组成部分。以自主移动平台（以下简称平台）为载体，集各种传感器于一身的智能装备可替代人工劳动，定时对畜牧环境进行巡检和环境监测是未来畜牧环境监测的一个重要发展方向。而以平台为主的类机器人轨迹跟踪也成为重要的研究方向。

移动机器人和无人驾驶车辆的轨迹跟踪问题，在过去数十年中得到广泛研究[2]。在国内，宋立博等[3-9]通过对移动机器人的运动学模型进行分析，并提出不同工作环境和场景下移动机器人的轨迹跟踪算法，并通过仿真取得较好的效果，但所提出的算法只是理论分析和仿真，没有通过试验验证其算法。李逃昌等[10-11]应用纯数学跟踪方法对农业移动机器人作业路径进行跟踪试验，由于定位的难度高导致定位的精度较差，并且存在较大的控制迟滞性，因此跟踪精度不高。在国外，Oriolo等[12]研究了无障碍环境下移动机器人的运动控制问题，通过线性化反馈控制双轮差动移动机器人，相较于具有非完整约束特性的移动机器人而言，具有完整约束特性的双轮差动移动机器人的可控能力较强，控制更为简单。Velasco-Villa等[13]针对移动机器人的轨迹跟踪问题，提出了一种基于室内视觉绝对定位系统测量的局部状态反馈算法，并在试验平台上证明了该算法的准确性，但是该定位方式具有局限性，不能很好的解决光线较暗环境下移动机器人轨迹跟踪问题。Del Rio等[14-15]通过建立移动机器人的运动学和动力学模型，采用直接控制移动机器人执行器输出的力的大小方法，实现移动机器人速度和转向控制，但在实际应用中，难以对移动机器人的力学模型进行具体量化分析，因此，很难被运用到实际工程中。在应用领域，近年来，随着仓储物流的快速发展，国内外仓库内使用搬运移动机器人（automated guided vehicle）对物品或者货架进行搬运成为了主流，但在畜牧养殖环境监测领域暂未发现有移动机器人的研究和使用。

针对上述问题，本文采用平台搭载环境监测传感器方法，定时巡检和监测畜牧环境信息。所研究的平台可归类为非完整约束移动机器人，对具有非完整约束的移动机器人轨迹跟踪控制的研究，是解决畜牧环境监测平台轨迹跟踪控制的重要途径[16-24]。通过对平台的运动学模型和误差模型分析，提出基于现Lyapunov函数和反推（Backstepping）时变状态反馈轨迹跟踪控制算法，使平台按照预定的轨迹进行运动和巡检，此期为畜牧环境监测自主移动平台轨迹跟踪提供参考。

1 系统结构与模型

1.1 平台装置结构

平台由安全检测系统、传感器、电气设备、I/O模块、工控机、电源、上位机等组成。平台长宽高尺寸分别为0.5 m×0.4 m×0.77 m，质量30 kg。平台由4个轮组成，分别为2个转向轮和2个驱动轮。轴距为0.35 m。转向轮通过舵机驱动实现转向，转向角范围为−0.52～0.52 rad，在实际运动过程中，为保护其转向机械结构，取转向角范围为−0.49～0.49 rad。驱动轮采用直流伺服电机驱动，驱动速度范围为0～0.3 m/s。平台采用激光定位方式，顶部安装激光定位传感器NAV350。具体结构如图1所示。

1.急停开关 2.状态指示灯 3.激光定位扫描仪NAV350 4.激光避障传感器 5.I/O模块 6.工控机 7.绝对值式角度编码器 8.转向轮 9. 24V铅蓄电池 10.驱动轮

1.Quick stop switch 2.State indicator lamp 3.Laser positioning scanner NAV350 4.Laser obstacle avoidance sensor 5.I/O module 6.Industrial control machine 7.Absolute value angle encoder 8.Steering wheel 9. 24 V lead-acid battery 10.Drive wheel

a. 自主移动平台系统实物图

a. Physical figure of autonomous mobile platform system

1.驱动轮 2.状态指示灯 3.转向轮 4.工控机 5.激光避障传感器 6.激光定位扫描仪NAV350 7.急停开关

1.Drive wheel 2.State indicator lamp 3.Steering wheel 4.Industrial control machine 5.Laser obstacle avoidance sensor 6.Laser positioning scanner NAV350 7.Quick stop switch

b. 自主移动平台结构简图

b. Structure diagram of autonomous mobile platform

图1 自主移动平台系统结构图

Fig.1 Autonomous mobile platform system structure diagram

当平台运行时，状态指示灯亮绿灯，NAV350扫描周围环境检测反光标贴，获取平台全局坐标实时位姿，角度编码器和速度传感器分别实时获取转向轮转角大小与平台运动速度大小。传感器采集的数据通过I/O模块输入工控机，系统获取各个传感器数据。

1.2 平台运动学模型分析

假设室内路面平坦、运动速度可变，平台为实心轮胎并无侧偏、无纵侧滑移，根据运动学原理，建立如图2所示的运动学关系模型。

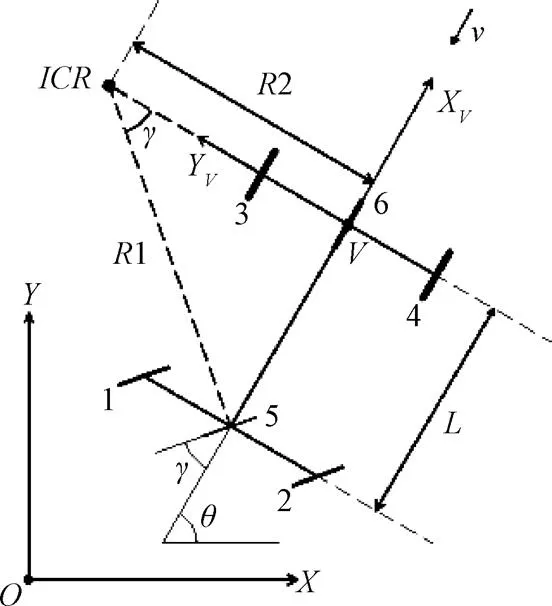
注：(X,O,Y)为笛卡尔全局坐标系；(XV,V,YV)为平台局部坐标系；1,2为转向轮；3,4为驱动轮；5为等效转向轮；6为等效驱动轮；L为轴距，m；θ为平台航向角，rad；ICR为平台瞬时旋转中心；v为平台运动速度，m·s-1；γ为转向轮转角，rad；R2为平台瞬时旋转半径，m。

根据建立的平台运动学模型图，可简化为轮5和轮6组成的二自由度轮式自行车模型，其运动学方程式为：

式中()为平台运动学模型图2中点坐标，既驱动轮中心点坐标，，分别为平台在全局地图中的横坐标和纵坐标，m；为平台运动速度，m/s；为平台转动角速度，rad/s；为平台航向角，rad；为平台等效转向轮转角（简称转向角），rad；为平台驱动轮和转向轮轴距，m；式（1）表示平台的位姿=(,,)与运动速度和转向角之间的关系，根据其数学转化关系可有

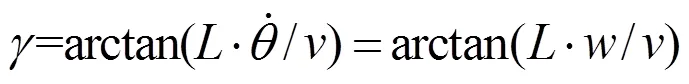
式（2）表示转向角与平台轴距，平台转动速度和移动速度之间的关系，在控制模型中以和为控制输出量，和的数值经过式（2）转化为平台转向轮转角和为输出控制量。对于本平台，控制其转向轮转角是控制运动方向最直接最简单的方式。

1.3 平台误差模型分析

式（3）为式（1）的矩阵表示形式。

在轨迹跟踪过程中，平台能够沿着期望轨迹运动，需要用到全局坐标中2个点，分别是参考点P(reference point)和当前点P(current point)，其中参考点P=(x,y,θ)T为期望轨迹上的点即目标点位姿，参考点即是目标点，P=(x,y,θ)T是平台当前位姿点坐标，定义误差向量P=(x,y,θ)T，P为目标点位姿向量P与当前点位姿向量P的误差值向量。根据图3几何关系得

式中x，y为平台当前点的坐标，m；x，y为目标点的坐标，m；x，y为目标点和当前点的误差值，m；θ，θ，θ分别为当前点的姿态角、目标点姿态角和误差姿态角，rad。式（4）用矩阵形式表示可得

式中T为正交矩阵，设参考点的速度和转速为q=(v,w)，当前平台的速度和转速为q=(v,w)，并设定q=(v,w)= (,)=。由式（3）可得

结合式（6）对式（5）进行时间求导并化简可得如下微分方程

式中v和v分别为平台当前点的速度和期望点的速度，m/s；w和w分别为平台当前点的转速和期望点的转速，rad/s。

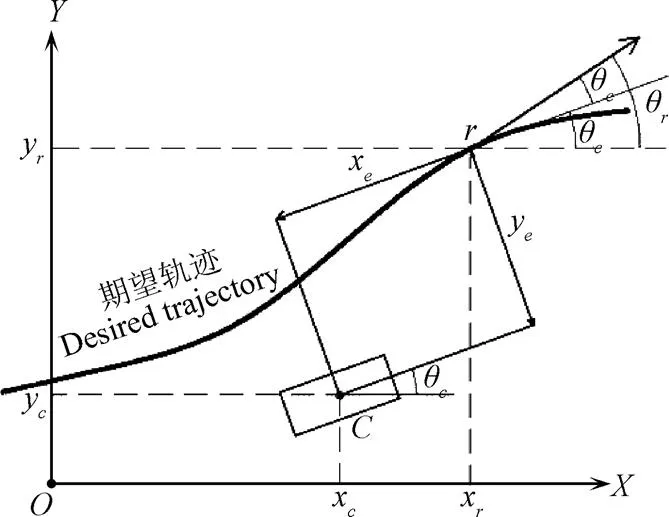
注：平台当前位姿为C(xc,yc,θc)；平台目标点位姿为r(xr,yr,θr)；误差量为Pe(xe,ye,θe)。

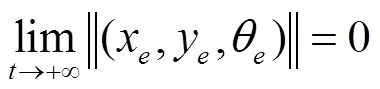
1.4 轨迹参考点的选择

参考点P的选择是建立误差模型的前提，也是平台能够快速收敛于期望轨迹的关键，如图4所示为本研究平台参考点的选择方法。

注：交点r1，r2；半径R1，R2，m；圆心C1，C2；平台当前的位姿C1(xc,yc,θc)；航向角误差值α，rad。

根据以上描述，可利用如下公式进行计算

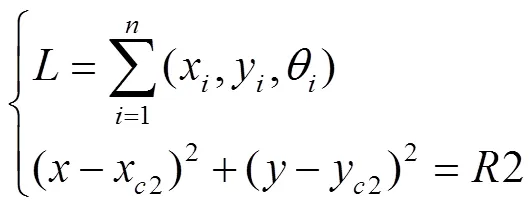
式中1为圆1半径，m；2为圆2半径，m；x2，y2为切点2坐标，m；x，y是以点2为圆心半径为2的圆与曲线的交点坐标，m；为平台的航向角误差值，rad。

根据式（8）求出唯一解2，式（9）求出各相交点1和2的坐标，式（10）求得航向角差值，最后判断参考点，完成参考点P的选择。

2 控制器的设计

2.1 平台轨迹跟踪控制系统设计

平台轨迹跟踪控制采用分层控制的思想，分为上层控制器设计和底层执行器控制。本文研究上层控制器的设计，底层控制采用PID控制，平台轨迹跟踪控制系统结构如图5所示。

由图5可知，系统的输入为位姿参数变量P，P和运动参数变量q，q，输出为下一刻的线速度v(t+1)和角速度w(t+1)即γ(t+1)。由于平台在运动过程中不可避免的出现偏移情况，因此平台的实时位姿不能用模型累积方法计算，模型累积计算得到的位姿会有累积误差，随着时间的推移，误差会增大，最终出现位姿错误，所以系统平台的位姿P是由激光定位传感器NAV350实时采集。P为平台参考点。T和P分别是式（5）中的转移矩阵和误差矩阵。q取值是根据前视点q所在曲线的曲率半径和平台的旋转半径进行设定。线速度和角速度数据q既是速度输出反馈量，也是轨迹跟踪控制器输入量。由结构图可知，只要设计准确的平台轨迹跟踪控制器，就能控制平台转向轮转角和速度，实现平台位姿的不断调整，最终使得系统误差向量P趋向于0。

注：Pr，Pc为位姿参数变量，Te，Pe分别为转移矩阵和误差矩阵，qr，qc为运动参数变量，vc(t+1)，wc(t+1)分别为线速度和角速度即γc(t+1)。

2.2 平台轨迹跟踪控制器设计

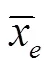
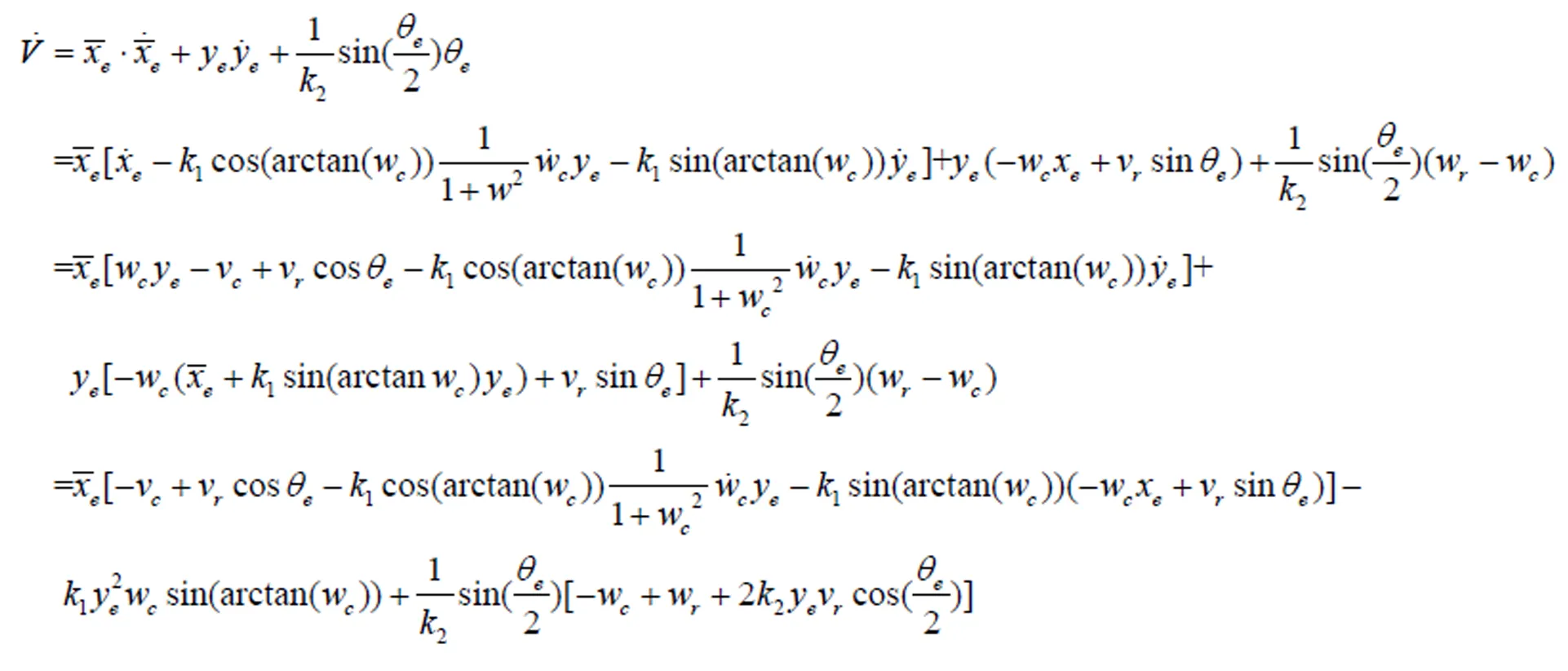
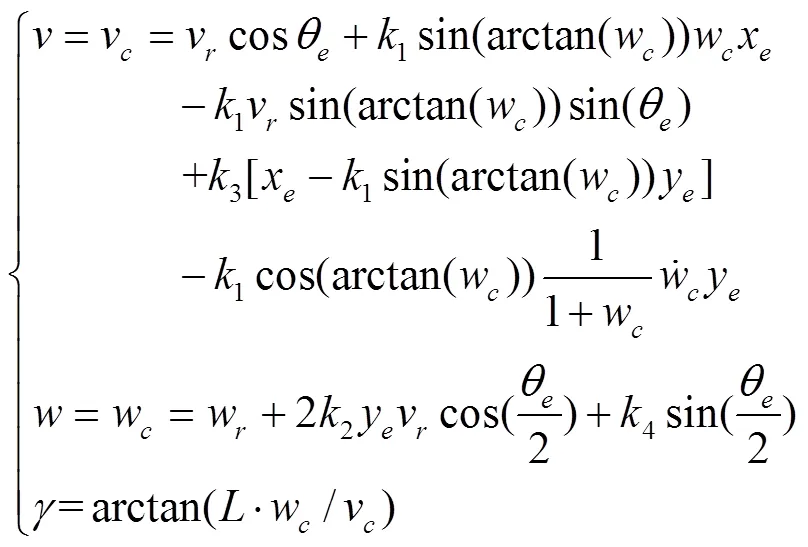
式中3,4为常数，且v≠0，有如下中间过程式：

将控制律式（14）带入式（13）中，整理得

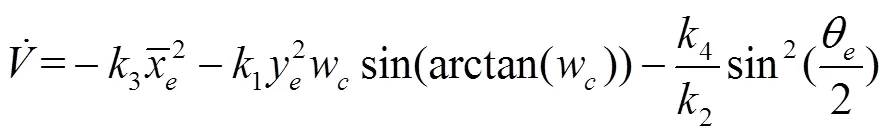
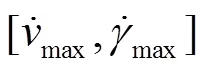
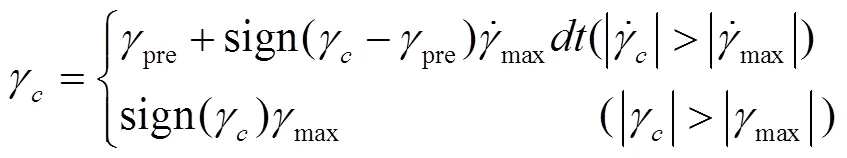
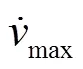
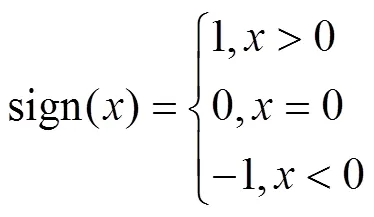
3 轨迹跟踪算法仿真

3.1 仿真环境和条件

仿真是在Matlab2015a环境下，应用控制律式（14）对平台的直线和圆周轨迹进行跟踪验证，式（14）中参数1,2,3,4为正的指数衰减时间常数，参数的取值影响平台轨迹跟踪收敛速度和稳定性。其中参数1,3调节横向误差x，2,4调节纵向误差y和位姿误差θ。

任意一条连续平滑的路径轨迹可以看成是由直线和圆弧轨迹拟合而成，用=f(x)+f(x)(,=0…)来表示，为起点到终点的期望轨迹函数，f(x)表示轨迹各直线函数段，f(x)表示轨迹各圆弧函数段。

3.2 直线轨迹跟踪仿真

在Matlab2015a环境下，采用编程方式对直线轨迹f(x)进行仿真。所跟踪的直线参考轨迹(期望轨迹)斜率为1.73(tan(π/3))，平台在全局坐标初始位姿为(x(0),y(0),θ(0))=(1 m, −1 m, 4π/9rad)，初始线速度和转向轮转角为(0,0)=(0 m/s, 0 rad)，初始参考点的位姿为(x(0),y(0),θ(0))=(1 m, −1 m,π/3 rad)，参考点线速度和转向轮转角为(v,γ)=(0.18 m/s,0 rad)，移动机器人轴距=0.35 m，系统参数(1,2,3,4)=(0.1,0.2,0.15,0.3)，平台直线轨迹跟踪仿真效果如图6所示。

图6 直线轨迹跟踪仿真结果

图6a表示平台在控制律式（14）的作用下，平台能够平稳地跟踪给定的直线轨迹；图6b表示随着平台不断收敛于期望直线轨迹过程中，其误差向量P=(x,y,)与时间的关系；图6c表示平台线速度、转向角与时间的关系。由图6中可看，平台直线轨迹仿真误差随时间增长而不断收敛，从第40秒开始，平台直线轨迹跟踪误差为x=±13.1 mm，y=±7.4 mm，=±0.75°，平台直线轨迹仿真获得较好的跟踪精度。

3.3 圆弧曲线轨迹跟踪仿真

同样在Matlab2015a环境下，对圆弧轨迹f(x)进行仿真，圆弧参考轨迹（期望轨迹）是圆心为(0,0)，半径为=1 m的圆。平台全局坐标初始位姿为(x(0),y(0),θ(0))= (1.8 m, -1 m, 2π/3rad)，初始线速度和转向角为(0,0)= (0 m/s, 0 rad)，初始参考点位姿为(x(0),y(0),θ(0))=(1 m, 0 m, π/2 rad)，参考点线速度和转向轮转角为(v,γ)=(0.18 m/s, 0.34 rad)，轴距=0.35 m，系统参数(1,2,3,4)= (0.1,0.2,0.15,0.3)，得到平台圆弧轨迹跟踪仿真效果如图7所示。

由图7中可看，平台圆弧轨迹仿真误差随时间增长而不断收敛，从第5秒开始，平台圆弧轨迹跟踪误差为x=±7.6 mm，y=±9.1 mm，=±0.52°。从图6和图7的仿真结果可以看出，在初始误差分别为x=10 mm，y=2 016 mm，=−19.9°和x=−80 mm，y=1 020 mm，=28.8°的情况下，根据控制律式（14）设计的控制器，能使平台平稳的收敛于期望轨迹，取得良好的跟踪效果。

图7 圆弧轨迹跟踪仿真结果

4 轨迹跟踪算法试验

4.1 试验材料和环境

试验在图1的平台上进行，在本试验中用到的相关仪器和材料：激光定位传感器NAV350，是德国Sick公司研发的一款具有建全局地图坐标系和定位功能的室内传感器，其定位精度达±4 mm，位姿角度测量范围是0～360°，数据采集频率为8 Hz；Beckhoff工控机，WIN7系统平台；I/O模块端子；24 V蓄电池；速度和角度编码器，型号同为CAX60-R13/12-E10-LB，分辨率为12bit/4096，重复精度为±2bit，信号输出范围4～20 mA；24 V直流伺服驱动电机，型号为57B2C1230-SCO，额定功率120 W，额定转速3 000 r/min；转向舵机，型号为LF20MG，旋转角度90°，扭矩2 N·m。

图8 平台执行器响应曲线图

试验软件是在WIN7系统上搭载的Microsoft visual studio/Twincat上进行，Twincat是德国Beckhoff公司开发的一个集成C/C++，PLC，matlab/simulink 3种可编程、算法设计和人机交互界面制作平台，且各编程语言之间数据可通过接口实现交换，是一个功能强大的嵌入式开发平台。

试验在图9中以长和宽分别为11.4和5.6 m的长方形场地中进行，场地中布置有7个直径均为90 mm的柱形反光标贴。激光定位传感器NVA350使用的环境条件是室内或者无强自然光影响的室外环境，因此试验时要求环境无太阳光直接照射，图9a的试验环境中无太阳光照射，可模拟畜牧环境场地，满足轨迹跟踪试验环境要求。

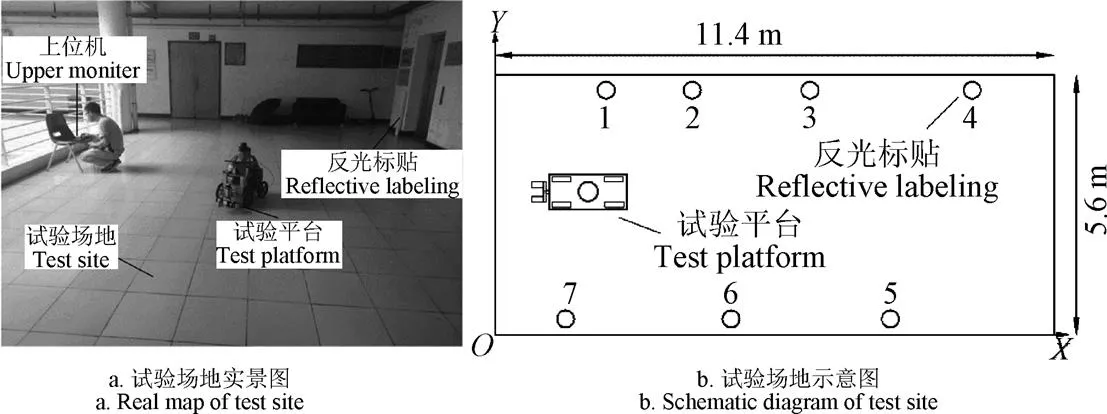
图9 试验场地图

4.2 平台轨迹跟踪试验

为验证轨迹跟踪算法和仿真的准确性，将采用上述设计的控制器在平台上进行试验，试验分为直线轨迹跟踪和圆弧轨迹跟踪2种验证性试验，以及单函数轨迹跟踪和分段函数轨迹跟踪2种应用性试验，验证性试验收集其运动轨迹、位姿误差变化和平台速度与转向轮转角数据，应用性试验收集其运动轨迹跟踪情况。

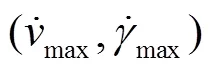
1）验证性试验。通过验证性试验得到的结果与仿真结果进行比较，进一步验证仿真的准确性，先进行直线轨迹跟踪试验，试验平台初始点为(x(0),y(0),θ(0))= (−4.73 m, −0.25 m,1.73 rad)，初始线速度和转向轮转角为(0,0)=(0 m/s, 0 rad)，初始参考点的位姿为(x(0),y(0),θ(0))= (2.44 m, 2.44 m, π/4 rad)，参考点线速度和转向轮转角为(v,γ)=(0.18 m/s, 0 rad)。跟踪的直线轨迹函数为=。图10为平台跟踪直线轨迹的试验结果。

图10中各图曲线是数据在Matlab中以图形的形式显示，其数据均来源于Twincat中示波器scope模块的记录，数据采集频率为100 Hz，本次试验总共获取5 358组数据。从图10b中可以看出，当运行时间大约为25 s时，位姿误差开始向0收敛，根据数据记录，从第25秒开始平台直线轨迹跟踪误差为x=±6.2 mm，y=±8.3 mm，=±4.2°，获得良好的直线轨迹跟踪精度。

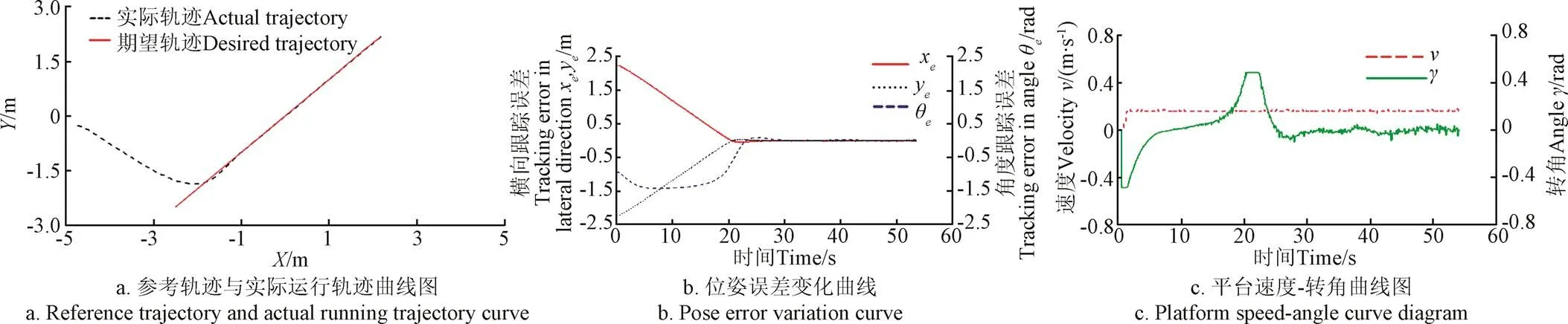
图10 直线轨迹跟踪试验结果

在进行圆弧轨迹跟踪试验时，设置跟踪的圆弧轨迹半径为=1.5 m，圆心为(0,0)。试验平台的初始点为(x(0),y(0),θ(0))=(-3.85 m, 0.04 m, -0.35 rad)，初始线速度和转向轮转角为(0,0)=(0.04 m/s, 0.49 rad)，初始参考点的位姿为(x(0),y(0),θ(0))=(-1.49 m, −0.15 m, −π/2 rad)，参考点线速度和转向轮转角为(v,γ)=(0.18 m/s,0.24 rad)，系统控制器保持参数不变。图11为平台跟踪圆弧轨迹的试验结果。

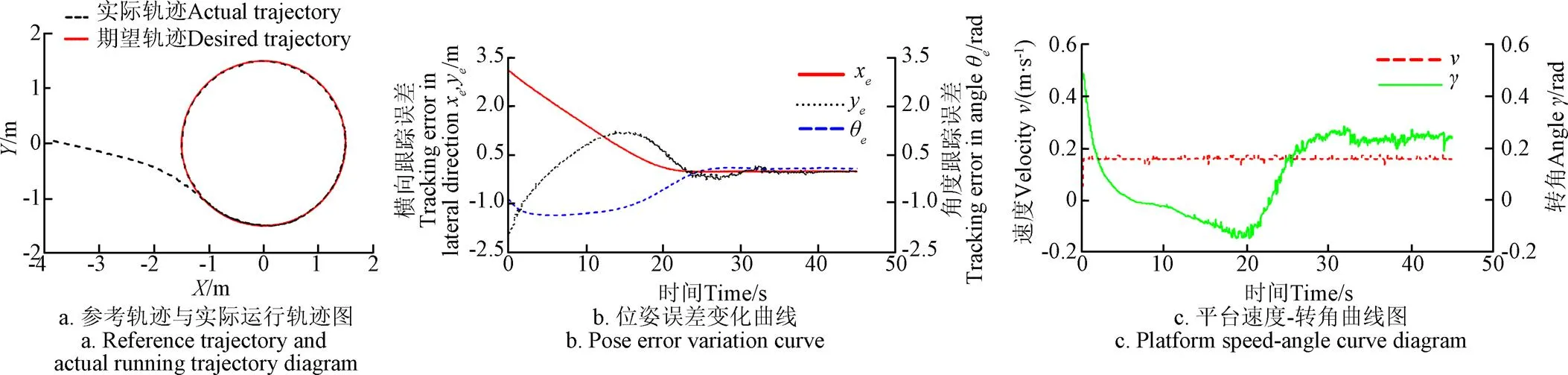
图11 圆弧轨迹跟踪试验结果

圆弧轨迹跟踪试验中采集到4501组数据，由图11b中可以看出，从第30秒开始，平台位姿误差向0收敛。从第30秒开始，平台圆轨迹跟踪误差为x=±7 mm，y=±9.8 mm，θ=±5.8°，获得较好的圆弧轨迹跟踪精度。

2）应用性试验，通过对一般轨迹的跟踪，观察其在工程上的应用效果。图12分别是轨迹为正弦函数=sin()和直线与圆弧组成的分段函数轨迹，其他系统参数不变。

图12 任意函数轨迹跟踪试验结果

从图12a中可以看出，平台在正弦函数的波峰和波谷时，并不能够完全沿着期望轨迹进行运动，这是由于平台本身机械结构即前轮转向转角的极限值限制(−0.49～0.49 rad)。从图12的轨迹跟踪试验得出，在初始误差分别为x=15 mm，y=385 mm，=−23°和x=−15 mm，y=757 mm，=10°的情况下，平台在控制器的调节下均能较快速地跟踪期望轨迹，使平台轨迹跟踪误差快速收敛，获得较好的轨迹跟踪精度和稳定性。

5 结论与讨论

1）开发了可实现畜牧环境监测的自主移动平台，提出了一种可实现自主移动平台轨迹跟踪的算法，并通过仿真验证算法的可靠性，试验验证了算法的有效性和稳定性，并使平台较快收敛于期望轨迹。能够满足工程应用的需求。

2）建立了平台运动学模型及其误差模型，提出平台轨迹参考点的选择方法，为平台轨迹跟踪算法的开发和期望点的选择提供了参考。

4）当控制器的系统参数为(1,2,3,4)= (0.1,0.2,0.15,0.3)时，仿真结果表明，当平台轨迹跟踪稳定后其直线跟踪误差为x=±13.1 mm，y=±7.4 mm，=±0.75°，圆弧轨迹跟踪误差为x=±7.6 mm，y=±9.1 mm，=±0.52°，能够较好的跟踪期望轨迹。验证试验和应用性试验结果表明，当系统参数不变，跟踪直线轨迹时，跟踪稳定后，其误差为x=±6.2 mm，y=±8.3 mm，=±4.2°，跟踪圆弧轨迹时，跟踪稳定后，其误差值x=±7 mm，y=±9.8 mm，=±5.8°，平台具有较好的跟踪稳定性和跟踪效果。该算法为平台和移动机器人的轨迹跟踪控制提供了理论依据，为工程实现提供了参考。

本文是基于平台为4轮机构，转向方式为前轮转向模型的前提下，采用基于Lyapunov函数和反推法（Backstepping）时变状态反馈控制方法的轨迹跟踪算法，解决畜牧养殖环境监测平台轨迹跟踪问题，该平台与传统的差速转向平台或机器人不同的是，它是通过控制方向轮的方向来改变平台的运动方向，具有非完整约束的特性，在实际工程应用中，该控制方式容易使平台运动出现偏移和车轮打滑现象，因此需要定位精度和实时性较高的定位装置，才能保证平台的运动精度。在平台运动过程中，转向轮存在小角度快速左右转动情况，经分析，这与控制器输出的控制转向轮转角数据快速波动有关。该控制算法较为复杂，想要平台获得较快的系统响应，需要性能较高的硬件设备，才能满足系统的实时性，成本较高。因此，下一步可通过改变方向控制方式和简化算法，降低算法的复杂性对系统硬件的需求，并采用滤波的方式减少输入和输出数据的波动，解决转向轮转角快速左右转动问题，提高平台的综合性能，降低成本。

[1] 陆明洲，沈明霞，丁永前，等. 畜牧信息智能监测研究进展[J]. 中国农业科学，2012，45(14)：2939－2947.

Lu Mingzhou, Shen Mingxia, Ding Yongqian, et al. Review on the intelligent technology for animal husbandry information monitoring[J]. Scientia Agricultura Sinica, 2012, 45(14): 2939－2947. (in Chinese with English abstract)

[2] Tua Agustinus Tamba, Bonghee Hong, Keum-Shik Hong. A path following control of an unmanned autonomous forklift[J]. International Journal of Control, Automation, and Systems, 2009, 7(1): 113－122.

[3] 宋立博，李劲松. 轮式移动机器人嵌入式自适应控制器设计与仿真[J]. 控制理论与应用，2012，29(9)：1147－1151.

Song Libo, Li Jinsong. Design and simulation of embedded model-free adaptive control system of wheeled mobile robots[J]. Control Theory & Applications, 2012, 29(9): 1147－1151. (in Chinese with English abstract)

[4] 鄢立夏，马保离. 轮式移动机器人的位置量测输出反馈轨迹跟踪控制[J]. 控制理论与应用，2016，33(6)：763－771.

Yan Lixia, Ma Baoli. Out feedback trajectory tracking control of wheeled mobile robots with position measurements[J]. Control Theory & Applications, 2016, 33(6): 763–771. (in Chinese with English abstract)

[5] 吕学勤，张轲，吴毅雄. 轮式移动焊接机器人输出反馈线性化控制[J]. 机械工程学报，2014，50(6)：48－54.

Lü Xueqing, Zhang Ke, Wu Yixiong. Control of thewheeled mobile welding robot based on output feedback linearization[J]. Chinese Journal of Mechanical Engineering, 2014, 50(6): 48－54. (in Chinese with English abstract)

[6] 和永智，刘伟军，周船，等. 轮式移动机器人与地形交互运动仿真研究[J]. 机器人，2007，29(5)：498－504.

He Yongzhi, Liu Weijun, Zhou Chuan, et al. Simulation of mutual motion between wheeled mobile robotsand terrains[J]. Robot, 2007, 29(5): 498－504. (in Chinese with English abstract)

[7] 王仲民，岳宏，刘继岩. 轮式移动机器人轨迹跟踪控制[J]. 太原理工大学学报，2005，36(4)：474－476.

Wang Zhongmin, Yue Hong, Liu Jiyan. Trajectory tracking control on wheeled mobile robot[J]. J of Tai yuan Univ of Tech, 2005, 36(4): 474－476. (in Chinese with English abstract)

[8] 庞海龙，马保离. 不确定轮式移动机器人的任意轨迹跟踪[J]. 控制理论与应用，2014，31(3)：285－292.

Pang Hailong, Ma Baoli. Adaptive unified controller of arbitrary trajectory tracking for wheeled mobilerobots with unknown parameters[J]. Control Theory & Applications, 2014, 31(3): 285－292. (in Chinese with English abstract)

[9] 吴卫国，陈辉堂，王月娟. 移动机器人的全局轨迹跟踪控制[J]. 自动化学报，2001，27(3)：326－331.

Wu Weiguo, Chen Huitang, Wang Yuejuan. Global trajectoty tracking control of mobile robots[J]. Acta Automatica Sinica, 2001, 27(3): 326－331. (in Chinese with English abstract)

[10] 李逃昌，胡静涛，高雷，等. 基于模糊自适应纯追踪模型的农业机械路径跟踪方法[J]. 农业机械学报，2013，44(1)：205－210.

Li Taochang, Hu Jingtao, Gao Lei. Agricultural machine path tracking method based on fuzzy adaptive pure pursuit model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1): 205－210. (in Chinese with English abstract)

[11] 张智刚，罗锡文，赵祚喜. 基于Kalman 滤波和纯追踪模型的农业机械导航控制[J]. 农业机械学报，2009，40(增刊)：6－12.

Zhang Zhigang, Luo Xiwen, Zhao Zuoxi, et al. Trajectory tracking control method based on Kalman filter and pure pursuit model for agricultural vehicle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(Supp.): 6－12. (in Chinese with English abstract)

[12] Oriolo G, De Luca A, Vendittelli M. WMR control via dynamic feedback linearization: Design, implementation, and experimental validation[J]. IEEE Transactions on Control Systems Technology, 2002, 10(6): 835－852.

[13] Velasco-Villa M, Aranda-Bricaire E, Rodrigu-Ezcortesh, et al. Trajectory tracking for a wheeled mobile robot using a vision based positioning system and an attitude observer[J]. European Journal of Control, 2012, 18(4): 348－355.

[14] Del Rio F D, Jim Enez G, Sevillano J L, et al. Error adaptive tracking for mobile robots[C]//The 28th IEEE Annual Conference of the Industrial Electronics Society, Sevilla, Spain: IEEE, 2002, 3: 2415－2420.

[15] Jiang Z P, Henk N R. Tracking control of mobile robots: a case study in backstepping[J]. Automatica, 1997, 33(7): 1393－1399.

[16] Fierro R, Lewis F L. Control of a nonholonomic mobile robot: backstepping kinematics into dynamics[C]//IEEE Proceedings of 34th Conference on Decision and Control, 1995: 3805－3810.

[17] 徐俊艳，张培仁. 非完整轮式移动机器人轨迹跟踪控制研究[J]. 中国科学技术大学学报，2004，34(3)：376－380.

Xu Junyan, Zhang Peiren. Research on trajectory tracking control of nonholonomic wheeled mobile robots[J]. J of Univ of Sci and Tech of China, 2004, 34(3): 376－380. (in Chinese with English abstract)

[18] 刘磊，向平，王永骥，等. 非完整约束下的轮式移动机器人轨迹跟踪[J]. 清华大学学报，2007，47(S2)：1884－1889.

Liu Lei, Xiang Ping, Wang Yongji, et al. Trajectory tracking of a nonholonomic wheeled mobile robot[J]. Journal of Tsinghua University, 2007, 47(S2): 1884－1889. (in Chinese with English abstract)

[19] Spandan Roy, Sanbhunath Nandy, Ranjit Ray, et al. Robust path tracking control of nonholonomic wheeled mobile robot: experimental validation[J]. International Journal of Control, Automation and Systems, 2015, 13(4): 897－905.

[20] Morin P, Samson C. Control of nonholonomic mobilerobots based on the transverse function approach[J]. IEEE Transactions on Robotics, 2009, 25(5): 1058－1073.

[21] Ailon A, Zohar I. Control strategies for driving a group of nonholonomic kinematical mobile robots in formation along a time parameterized path[J]. IEEE/ASME Transaction on Mecha-tronics, 2012, 17(2): 326－336.

[22] Fierro R, Lewis F L. Control of a nonholonomic mobile robot: Backstepping kinematics into dynamics[C]// Procee-dings of the IEEE Conference on Decision and Control, New Orleans, LA, USA, 1995: 3805－3810.

[23] Azza El-sayed Bayoumo Ibrahim. Wheeled mobile robot trajectory tracking using sliding mode control[J]. Journal of Computer Sciences, 2016, 12(1): 48－55.

[24] Kanayama Yutaka. A stable tracking control method for a non-holonomic mobile robot[J]. IEEE/RSJ International Workshop on Intelligence Robots and Systems, 1991, 91: 3－5.

[25] 闵颖颖，刘允刚. Barbalat引理在系统稳定性分析中的应用[J]. 山东大学学报：工学版，2007，37(1)：51－56.

Min Yingying, Liu Yungang. Barbalat lamma and its application in analysis of system stability[J]. Journal of Shandong University : Engineering Science, 2007, 37(1): 51－56. (in Chinese with English abstract)

[26] Jiang Z P, Nijmeijer H. Tracking control of mobile robots: A case study in backstepping[J]. Automatica, 1997, 33(7): 1393－1399.

[27] 李世华，田玉平. 移动小车的有限时间轨迹跟踪控制[J]. 东南大学学报：自然科学报，2004，34(1)：113－116.

Li Shihua, Tian Yuping. Trajectory tracking control of mobile robots in finite time[J]. Journal of Southeast University: Natural Science Edition, 2004, 34(1): 113－116. (in Chinese with English abstract)

[28] 朱奇光，王佳，张朋珍，等. 基于高斯矩改进SURF算法的移动机器人定位研究[J]. 仪器仪表学报，2015，36(11)：2451－2457.

Zhu Qiguang, Wang Jia, Zhang Pengzhen, et al. Research on mobile robot localization based on gaussian moment improved SURF algorithm[J]. Chinese Journal of Scientific Instrument, 2015, 36(11): 2451－2457. (in Chinese with English abstract)

Trajectory tracking algorithm of autonomous mobile platform for animal husbandry environment information monitoring

Lü Enli1,2, Wei Jianfeng1, Wang Yu1,2, Zhao Junhong1, Wang Feiren1, Liu Yanhua3※

(1.510642,; 2.510642,; 3.,510642,)

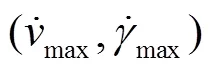
environmental monitoring; algorithms; models; autonomous mobile platform; trajectory tracking; kinematic model; lyapunov function; beckstepping

吕恩利，韦鉴峰，王 昱，赵俊宏，王飞仁，刘妍华. 畜牧养殖环境监测自主移动平台轨迹跟踪控制算法[J]. 农业工程学报，2018，34(13)：86－94. doi：10.11975/j.issn.1002-6819.2018.13.011 http://www.tcsae.org

Lü Enli, Wei Jianfeng, Wang Yu, Zhao Junhong, Wang Feiren, Liu Yanhua. Trajectory tracking algorithm of autonomous mobile platform for animal husbandry environment information monitoring[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(13): 86－94. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.13.011 http://www.tcsae.org

2018-01-17

2018-05-10

国家科技支撑计划课题（2015BAD18B0303）；现代农业产业技术体系建设专项资金（CARS-33-13）；国家自然科学基金项目（51108194）

吕恩利，副教授，博士生导师，主要研究方向为农业工程、农产品冷链物流装备、智能仓储运输装备控制研究。 Email：enlilv@scau.edu.cn

刘妍华，博士，副教授，主要研究方向为农产品冷链物流和农业设施节能设计。Email：cynthial@scau.edu.cn

10.11975/j.issn.1002-6819.2018.13.011

TP23

A

1002-6819(2018)-13-0086-09