含多间隙柔性可展帆板动力学建模及仿真

2018-08-10邱雪松任志博魏亚坤

宇航学报 2018年7期

邱雪松，任志博，桂朋，魏亚坤

(燕山大学机械工程学院，秦皇岛 066004)

0 引言

太阳帆板作为月球车的重要部件[1]，其展开过程动态特性不仅影响帆板自身的展开精度及可靠性，同时会对月球车本体上精密仪器的工作产生强烈干扰，直接影响月球车性能。而帆板结构的柔性和各级帆板铰链间隙则是导致帆板在展开过程中呈现复杂动力学行为的重要因素。目前，太阳帆板逐渐向轻质化和柔性化发展[2]，且含隙铰对可展机构的不利影响已在多种空间机构中体现，影响系统的精确运行。因此可展机构的动力学建模必须考虑铰间隙和柔性因素的影响。

目前，学者在建立各类含间隙机构动力学模型时多考虑了结构柔性的影响，并进行了深入的研究[3]。Schwabeta等[4]研究了转动副间隙机构的动态响应，分别建立了含刚性构件、柔性构件的模型，并介绍了一种估算间隙内碰撞产生的最大接触力的方法；Chunmeietal等[5]用统一的动态模型分析含间隙柔性四连杆机构的动态响应，并分析间隙和杆件弹性对机构动态特性的影响；考虑关节处元件柔性、间隙、摩擦的影响，Shiau等[6]分析了考虑间隙和构件柔性的并联机构的非线性动态特性；Khemili和Romdhane[7]研究了含间隙柔性曲柄滑块机构的动态特性，利用ADAMS进行仿真分析，并进行实验验证。结果表明：间隙对机构的响应有明显影响，且杆件的柔性缓解了间隙产生的影响；Bauchau和Rodrigez[8]两人研究了间隙和润滑对转动副和球副的影响，在能量守恒和衰减时间积分的基础上构建方程，通过数值实例校验了所用方法的有效性和准确性；Liu等[9]提出了一种近似模型描述间隙圆柱副接触性能。通过适当假设，分析有限元结果中的接触区域、压力以及最大持续应力，并将销作为刚性楔体以及将弹性板作为简单的温克勒弹性地基，最终建立了含间隙的圆柱副接触问题的近似模型；Erkaya和Uzmay[10]使用试验和理论的方法研究了间隙对机械振动和噪声的影响，结果表明含运动副间隙时的振动和噪音均高于不含间隙时；Flores等[11]通过数值和实验方法对含间隙曲柄滑机构的动态响应进行研究；赵和白[12]研究了含间隙空间机械手的动态特性，使用非线性等价弹簧阻尼模型建立了间隙接触模型；在考虑摩擦的情况下，利用库仑摩擦模型。Tian等[13]提出一种建立含圆柱副间隙的空间柔性多体系统模型的方法，即利用绝对坐标法建立柔性部件模型，使用自然坐标法建立刚性部分模型，研究圆柱铰链间隙处的干摩擦和润滑对系统动力性能的影响，通过两个例子校验了方法的正确性。郭军等[14]基于柔性杆件的有限段模型，使用拉格朗日方程建立了含刚性支座的双联杆柔性机械臂的刚、柔混合多体动力学模型。结果表明：该模型即可宏观上模拟柔性杆件的大范围刚体运动，又可以在微观层次上模拟各柔性臂的弹性变形。Oskar等[15]学者以柔性帆板为研究对象，利用SIMPACK软件分析了帆板柔性对可展机构展开过程的动力学特性影响。谷勇霞等[16]利用ADMAS软件建模分析了含柔性和间隙的二级太阳帆板展开过程的动力学行为，得出间隙数目的增加会增加铰链处碰撞的剧烈程度和频率的结论。孙红丽等[17]利用有限元方法对帆板进行离散化，使用Kane方程建立了柔性展开机构的动力学模型。史加贝等[18]基于共旋坐标法和板壳理论，建立了大型太阳电池阵展开过程的动力学模型。段柳成等[19]基于Jourdain速度变分原理和单向递推组集方法，建立太阳阵展开与锁定过程的刚柔耦合多体系统动力学模型，预测了太阳阵展开历程及航天器本体姿态扰动情况。

上述以一般环境的活动件或一次性空间可展机构为研究对象进行的研究，为具有柔性特征的含间隙机构的建模、仿真研究奠定了基础。结合月球车两级往复可展太阳帆板(下文简称可展帆板)在低重力条件下重复折展的工作特点，采用L-N模型描述运动副间隙引发的接触碰撞，使用修正库伦模型描述铰间隙的摩擦力，利用有限元法对帆板进行柔性化[20]，建立多间隙-柔性耦合的动力学模型，对其展开过程进行分析，为后续的非线性动态特性的深入研究提供前提，为改善多级可展太阳帆板性能、提高展开精度及可靠性提供理论基础。

1 可展帆板机构及工作原理

可展帆板主要由基体、内外帆板、同步传动机构等组成，参见图1。同步传动机构将钢丝绳内错缠绕并固定在两钢丝绳轮，使用伺服电机驱动，实现两级帆板同步异向展开。同步传动机构的两带轮半径相同以保证展开角速度大小相同。该驱动方式可控制帆板的展开角度、展开速度，实现帆板的重复折叠展开，以适应帆板月夜折叠、月昼展开的功能需求。含间隙铰链由滑动轴承和销轴组成，转动副的运动功能使得滑动轴承与销轴之间必然存在间隙。当帆板展开时，含隙铰的轴承与销轴因间隙而表现出偏心，从而引发二者间不断的分离-接触-碰撞冲击，进而影响系统的动态特性、帆板的展开精度及稳定性。由于可展帆板为平面机构，因此在建立帆板铰间隙模型时仅考虑径向间隙变化。

2 柔性可展帆板含隙铰模型

2.1 间隙描述

图2表达了机构运转时，铰间隙的一般状态，即由于轴套与轴颈的偏心引起二者的偏心斜碰撞，并因碰撞而产生弹性变形。建立绝对坐标系XOY，各矢量的位置见图2。

间隙偏心矢量e：

e=rO1-rO2=[ex,ey]T

(1)

轴承与销轴碰撞引起的碰撞变形即碰撞深度为：

(2)

式中：RO1,RO2分别为轴承与销轴的半径。

2.2 间隙铰模型

如图2所示，接触点P和Q的绝对坐标为：

(3)

则可得到法向速度和切向速度：

(4)

式中：n为偏心矢量的单位法向量，大小为

(5)

综合考虑能量损失、碰撞体材料、弹性变形等因素，采用L-N模型描述法向力：

(6)

式中：ce为恢复系数。

(7)

式中：νi为泊松比；Ei为弹性模量；σi为中间量。

为防止切向相对速度vt为0时接触力出现突变, 采用修正的Coulomb模型处理摩擦影响,切向摩擦力表达为：

(8)

式中：cf为静摩擦系数；cd为动摩擦系数：

(9)

式中：v0,v1为给定的速度极限值。

综上，间隙处接触碰撞力矢量Fp表达为：

Fp=(Fn+Ft)+

(10)

下标“+”表示当δ≥0表示轴套与轴颈发生接触碰撞，此时间隙处产生接触碰撞力；当δ<0表示间隙运动副元素间没有发生碰撞，此时间隙处没有产生接触碰撞力，即Fp= 0。

3 柔性可展帆板含间隙动力学模型

柔性可展帆板动力学模型是基于刚性可展帆板模型，采用有限元法对帆板进行柔性处理后建立，基本方法如下：

(1) 基于理想刚体，分析可展帆板运动特性。

(2) 基于刚性可展帆板运动分析，解析系统惯性力及瞬时外力。将帆板瞬时固定，施加惯性力及此瞬时外力，分析帆板瞬时的弹性变形运动。

(3) 将刚性可展帆板运动与可展帆板的瞬时弹性运动相互叠加，建立柔性可展帆板动力学模型。

3.1 刚性可展帆板含间隙动力学模型

由于二级帆板机构展开过程是平面运动，故将其简化为平面连杆机构。帆板等效处理后，受力如图3所示。

基于牛顿-欧拉法，建立可展帆板1，2的刚体动力学方程，分别如下:

(11)

式中：Rj2为销轴半径，j=A,B；Jm为绕m点的转动惯量，m=O2,O4；li为帆板i的长度；Gi为帆板i所受的重力；lsi为帆板i质心与铰链中心距离；θi为帆板i位姿角；φi为接触角；axi,ayi为帆板i质心沿X,Y方向的加速度；Ti为作用在帆板i上的转矩，i=1,2；F31x,F31y,F21x,F21y,F12x,F12y为间隙碰撞力。

3.2 可展帆板柔性化

假定杆单元的节点坐标为δ1,δ2,δ3,δ4,δ5,δ6，如图4所示。其上任一点H距节点1的距离为x，变形为u,w，写成矩阵形式为m=[uw]T,u,w分别为点H沿杆长方向以及垂直杆方向的变形。

基于上述假设，建立帆板1变形函数：

(12)

则可得到帆板1单元广义力：

(13)

式中：P1，P2分别为帆板1在X,Y方向上的惯性力，P3为绕帆板质心的惯性力矩。

则可建立帆板1的单元广义力矢量：

Q1=[Q1Q2Q3Q4Q5Q6]T

(14)

同理，可得到帆板2的单元广义力矢量Q2=[Q7Q8Q9]T，则可得到系统的单元广义力矩阵：

Q=[Q1Q2]T

(15)

根据形函数可以得到杆的弹性应变能U，动能T：

(16)

式中，E为帆板的弹性模量，A为帆板横截面积，I为截面惯性矩，ρ为单位长度的质量。

式(17)拉格朗日方程：

(17)

式中，Qn为节点坐标δn下的单元广义力。

将式(16)带入式(17)，可得到展开机构展开过程中的质量矩阵M，刚度矩阵K。

3.3 含双间隙柔性可展帆板动力学模型

基于刚性及弹性运动的等效运动叠加，建立含间隙柔性可展帆板动力学模型：

(18)

4 数值求解和结果分析

给定两级帆板展开运动规律：帆板1的运动规律为θ1=-0.25πcos(0.2πt)+0.25π，帆板2的运动规律为θ2=0.25πcos(0.2 πt)-0.25π。给定初始间隙值c=0.05 mm，摩擦系数cf= 0.01，帆板运行时长为5 s。其他相关参数见表1。

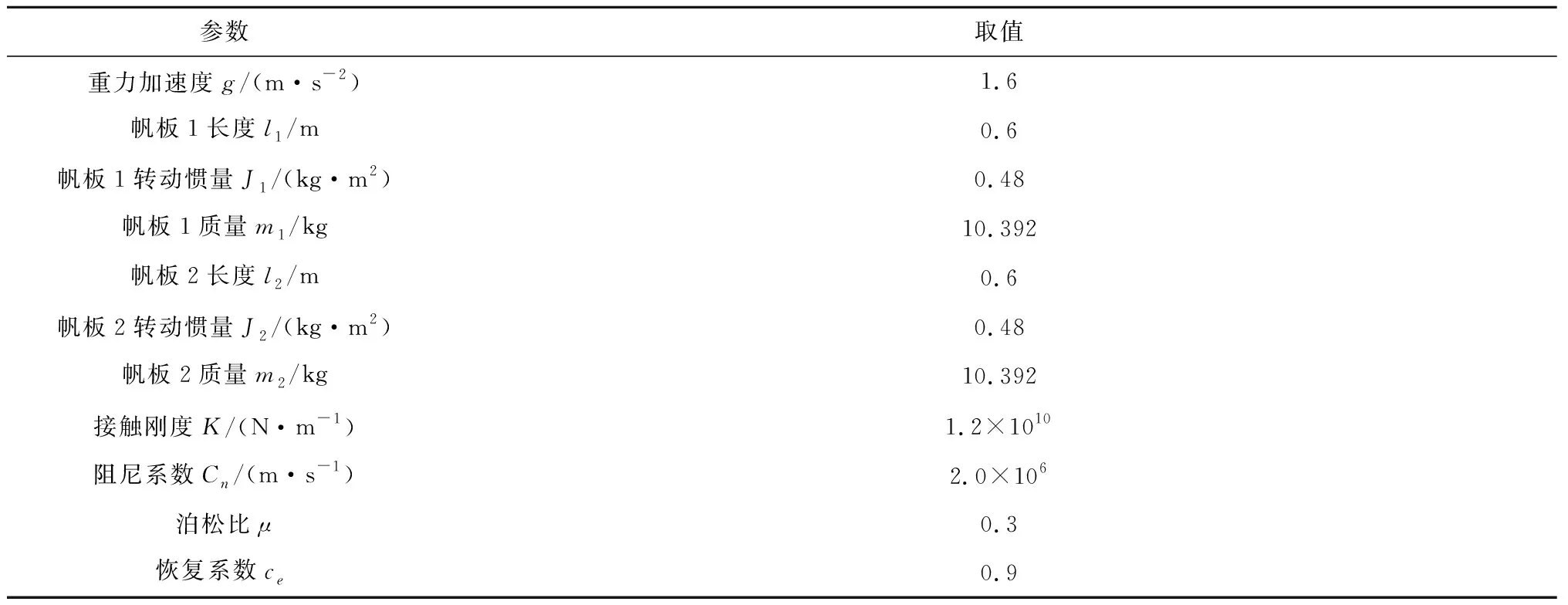
表1 可展帆板几何与惯性参数Tabble 1 Geometrical and inertial parameters of plane

含间隙可展帆板间隙处的碰撞一般为低速、频繁碰撞，可根据前后碰撞体穿透深度来判别碰撞。设δ(t)、δ(t+Δt)分别为t时刻和t+Δt时刻铰链间隙处碰撞体穿透深度，当δ(t+Δt)·δ(t)≤0成立时，可判定在时间Δt内间隙处运动副元素之间至少发生一次碰撞。利用MATLAB软件进行数值求解[21],数值求解过程如图6。

4.1 帆板柔性对帆板展开过程的影响

保持帆板展开规律不变，数值仿真分析帆板柔性变形对帆板展开过程的影响，参见图7和图8。图7表示帆板展开过程中柔性对帆板质心加速度的影响。结合图(a)、(b)分析可知，含间隙柔性可展帆板的质心加速度的上下波动，是由帆板弹性变形和铰链处间隙共同作用引起的。在帆板展开初始时期，对帆板质心加速度产生影响的因素中，间隙起主要作用；随着时间变化，间隙影响迅速减小，此时帆板弹性变形起主要作用。

图8为柔性引入对帆板间隙处碰撞力的影响。由图8(a)和(b)比较分析可知，帆板柔性会减弱间隙处碰撞的剧烈程度，减小碰撞力幅值，但帆板机构趋于平稳运行状态的时间明显延长，且达到平稳状态的过程中碰撞力变化是相对连续的。这是因为帆板柔性对碰撞有缓冲作用，减小了碰撞能量和能量损失速度，使碰撞-分离-碰撞的次数变多。

4.2 双间隙对帆板展开动态特性影响

保持展开规律不变，数值仿真分析单、双间隙对柔性帆板展开的影响。图 9显示销轴中心轨迹。比较图9(a)和(c)可知，机构中多间隙的存在，使铰链间隙缩小碰撞范围：比较图9(a)和(b)可知，间隙铰链相对于机架的位置直接影响铰链间隙碰撞的幅度及范围；且间隙的影响可叠加耦合至机架处铰链，引起其碰撞幅度及范围的减小。因此，多间隙的存在，引起铰链间隙动态特性耦合和远端间隙碰撞能量消耗，间接减小了机架处铰链间隙碰撞的范围。

图10显示帆板间隙处碰撞力的变化情况。比较图10(a)和(c)可知，多间隙的存在，增加了碰撞力峰值和碰撞频率，并使趋于稳定状态的时间缩短，但最终碰撞力的大小都稳定在200 N左右；比较图10(a)，(b)，(c)可知，间隙铰链相对于机架的位置直接影响铰链间隙处的碰撞力，且远端铰链间隙的影响可叠加耦合至机架处铰链间隙。因此，多间隙的存在可引起动态特性的耦合，增大铰链间隙的接触碰撞力。