基于改进型扰动观测器的IPMSM无传感器控制

周 静，杨振强，王继超

(1.大连理工大学，大连 116024；2.中国人民解放军31696部队，锦州 121017)

0 引 言

无位置传感器技术，可以通过建立合理的数学模型，替代传统的机械式编码器，获得电机的位置信息。由于此技术能降低系统成本，减小电机体积，降低运行环境要求，因此具有较高的研究价值[1-3]。

对比表贴式永磁同步电机(以下简称SPMSM)，内置式永磁同步电机(以下简称IPMSM)是嵌入式转子结构，具有可靠性强、调速范围大、效率高等优点，是目前发展的主流[4-6]。但是，IPMSM存在凸极效应，磁路非线性，电机数学模型相对复杂，在无位置传感器技术中，用于转子位置信息估计的观测器设计与调试过程相对复杂，不易于工程实现[7，8]，本文致力于解决此类问题。

近年来，随着科研工作者对无位置传感器技术研究的深入，取得了大量的研究成果。文献[9]提出了一种基于合成反电动势的滑模状态观测器，实现了IPMSM无位置传感器控制系统的高速稳态运行，但是在开关切换时容易引入高频信号，需要通过两级滤波器对其进行消除，调试起来复杂。文献[10]基于非线性观测器实现了IPMSM无位置传感器控制，转子位置与转速估算精度高，缺点是设计过程复杂、计算量大，且计算过程中需要借助状态的微分，导致噪声信号的放大，因此采用了低通滤波器，调节过程较复杂。文献[11]在一种新型的扰动观测器的基础上实现了SPMSM无位置传感器控制。其设计过程简单，结果精确，调试过程简单，容易应用。但是，其观测模型是基于SPMSM的电流状态方程搭建，因此不适用于IPMSM。

本文结合多种控制策略的优点，研究了一种基于改进型扰动观测器的IPMSM控制方法。此方法通过合成反电动势，得到与SPMSM相似的模型，再利用中间变量转换，在不添加滤波器的条件下求得理想的合成反电动势，将其与锁相环结合得到转子位置信息。利用一个随转速变化的误差补偿环节，消除了因为模型误差导致的转子位置估算误差。通过对仿真结果分析，此方法调试过程简单，能够精确地估计转子位置信息，从而完成高性能的IPMSM无位置传感器控制。

1 IPMSM数学模型

在静止α，β坐标下，IPMSM的电压方程如下：

可以将式(1)改写为矢量形式：

可以看出，因为IPMSM 的Ld,Lq不等，半差电感不为零，附加电压ηαβ受θe的影响，导致利用反电动势搭建观测器的无传感器技术不适用于IPMSM。因而，本文通过定义合成反电动势，使IPMSM的数学模型变成与SPMSM 相似的模型。

通过坐标变换理论，对附加电压ηαβ变换，可得：

式中:id为直轴电流。

通过将附加电压ηαβ分解成E1，E2，E3，由式(2)和式(3)可知，E2与反电动势Eαβ的相位相同，可以将其合并。

定义合成反电动势Esyn:

E3与反电动势Eαβ正交，而且和合成反电动势的相比，E3的幅值比较小，为了简化计算，可以将其忽略。

定义合成后的输入电压矢量vαβ：

将合成后的量代入式(1)，IPMSM 在α，β坐标系下的电压方程可以变形:

从而，得到以定子电流为状态变量的电机电流状态方程:

2 扰动观测器的设计

2.1 扰动观测器的数学模型

干扰下的时域微分方程：

式中：x是状态变量，u是输入量，d是扰动量；A,Bu及Bd分别是与x,u及d对应的系数矩阵。

在干扰信号d变化迟缓的情况下，d的导数约等于0，可以忽略。

估计误差：

对应的扰动观测器可以表示：

式中：L为扰动观测器的增益矩阵。

本文采用了文献[11]中利用中间变量转换的改进型扰动观测器，代入式(10)，可以得到：

定义中间变量：

从而，得到扰动观测器的模型：

由于借助中间变量z，扰动量的估计不用计算状态变量微分，所以不用额外设计滤波器对噪声信号进行消除，从而简化了观测器。

本文将静止α-β坐标下合成反电动势Esyn作为扰动量，建立基于合成反电动势的扰动观测器模型。

对式(7)的IPMSM电流状态方程整理可得：

从而，得到基于合成反电动势的观测器模型：

式中：l为扰动观测器的增益。

根据式(15)，作出的扰动观测器结构图如图1虚线框所示。

图1 基于扰动观测器的转子位置估计

由图1可知，定子电压和电流经过改进型扰动观测器可以估计出合成反电动势。由于合成反电动势中有IPMSM转子位置和速度信息，结合PLL与对应的位置补偿后可以实现对转子位置和速度较为精确地估计[12-14]。

根据式(4)可以推出:

式中：k=pωm(ψf+2L1id)。

合成反电动势利用PLL实现对转子速度的估计，估计出的速度量再通过积分便能够求得转子位置。

2.2 转子位置补偿

为了消除因为观测器模型误差导致的转子位置估算误差，需要进行转子位置补偿。

对式(10)作拉氏变换，推导出扰动观测器的传递函数：

因此，扰动观测器可等效为一阶惯性环节。

结合式(4)推出估计值：

得到转子位置补偿公式：

2.3 李雅普诺夫稳定性

扰动观测器的动态误差方程可以表示：

为了使速度估计误差能够收敛，定义式(22)李雅普诺夫函数。

对其求导：

l<0

3 仿真分析

本文采用型号为GK6080-6AC31的IPMSM，表1给出了IPMSM相关参数，图2为IPMSM控制系统的结构框图。

表1 IPMSM主要参数

图2 基于改进型扰动观测器的IPMSM无位置传感器控制系统结构框图

在MATLAB/Simulink平台上设计了系统的仿真模型，通过对基于改进型扰动观测器的IPMSM无位置传感器控制系统实行仿真，确定观测器增益，验证了观测器对转子信息的估计性能。

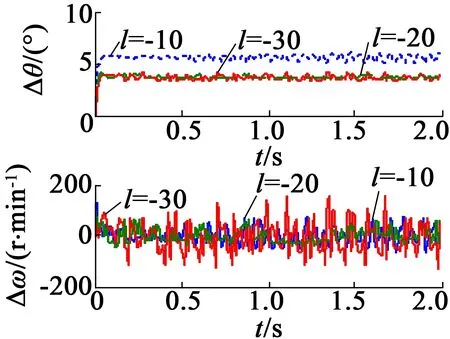
图3 不同增益下的转子误差

由此可知，增益越小，转子位置估计误差越小，但是转速误差波动越大。为获得较好的控制性能，系统选取的增益为-20。此增益选取方便，且产生的误差在系统允许误差范围内，满足系统要求。

选定增益后，讨论负载变化对系统的影响。在1 s时，突加负载转矩TL，TL的值分别取2 N·m，5 N·m，10 N·m。图4是负载变化对转速和位置误差的影响。由图4(a)可知，TL越大，转子速度下降的幅度越多，但仍能实现对给定转速的跟随。由图4(b)可知，TL越大，转子位置误差略有增加，转子位置误差最大不超过8°电角度。由此可知，观测器具有较强的鲁棒性。

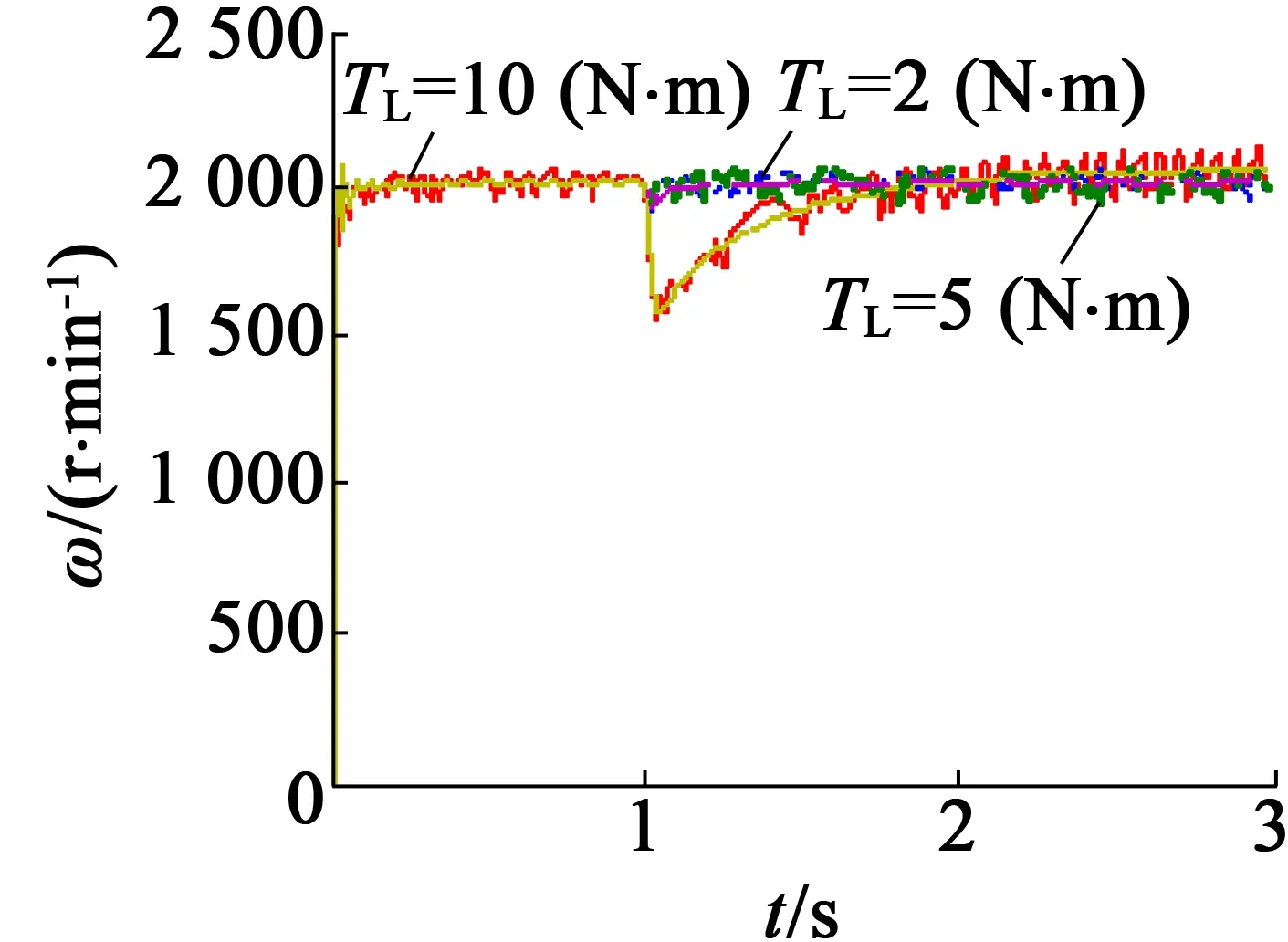
(a) 电机转速

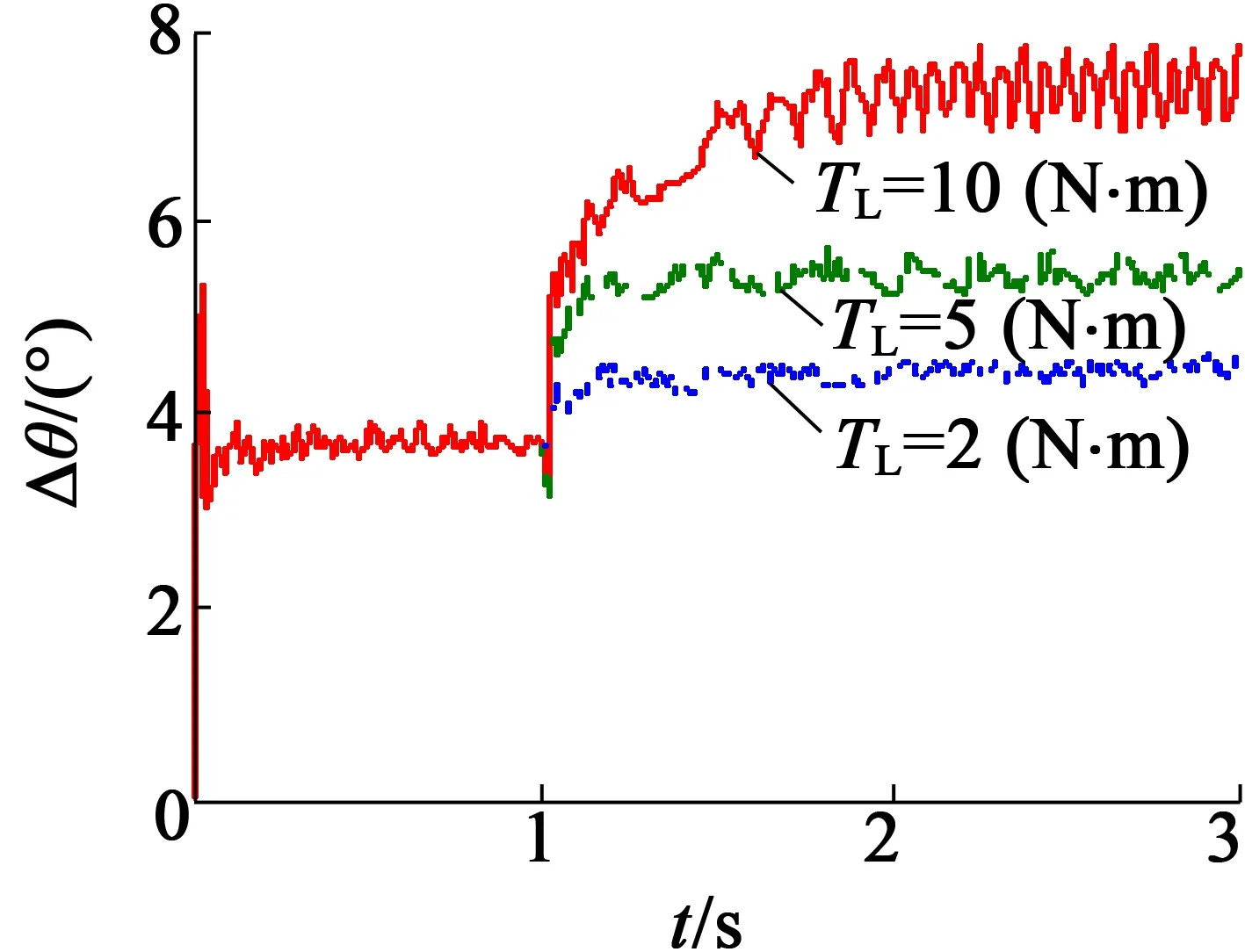
(b) 电机位置误差

系统仿真时间设为4 s，IPMSM稳态运行在TL=2 N·m条件下，在2 s时，将电机给定转速由500 r/min阶跃到2 000 r/min，系统波形如图5所示。从图5可以看出，估计转速能够对实际转速进行良好的跟随。在给定转速500 r/min 的情况下，转子的速度误差约±15 r/min，速度误差波动近似为3%。在给定转速2 000 r/min 的情况下，转子的速度误差近似为±50 r/min，速度误差波动约为2.5%，速度误差波动稍微有所减小，转子位置估计误差近似为4.6°电角度。

图5 转速阶跃变化时系统波形

为了进一步验证电机控制系统的性能，在1 s时，将IPMSM的转子速度在200 ms内，从500 r/min斜坡上升到2 000 r/min，运行后，再用同样的速率，降到500 r/min，系统波形如图6所示。

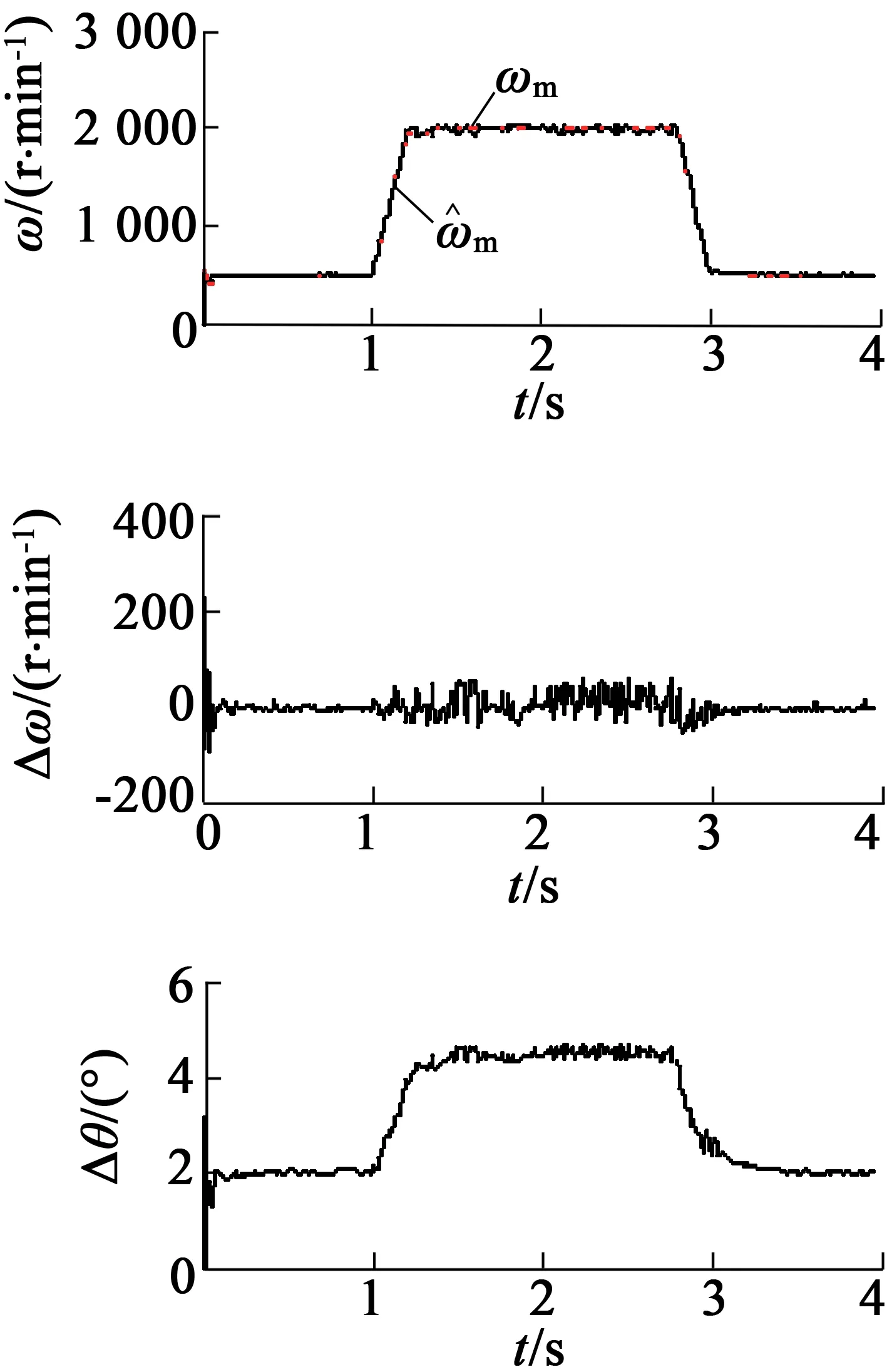
图6 转速斜坡变化时系统波形

从图6可以看出，在加减速过程中，估计转速同样能够对实际转速进行良好的跟随，转子速度动态误差小于50 r/min，静态误差小于15 r/min，始终不超过给定转速的3%，转子位置误差始终不超过4.6°电角度。

对比文献[9]和文献[10]中的观测器，此观测器设计相对简单，虽然转速误差波动略有增加，但是精度满足系统要求。

综上所述，此扰动观测器能够准确地估算转子位置和转速，实现了IPMSM高性能的运转。

4 结 语

本文基于改进型扰动观测器建立了IPMSM数学模型，将合成反电动势作为扰动量，利用中间变量，结合锁相环对转子位置和转速进行估算，实现了高性能的IPMSM无位置传感器控制。通过仿真分析了不同观测器增益和负载转矩对转子误差的影响，选择了合适的增益，完成了仿真验证，得到以下结论：

1) 改进型的扰动观测器利用中间变量，不用设计额外的滤波器，就可以估算出合成反电动势，模型设计与调试过程简单，易于工程实现，具有较高的应用价值。

2) 估算精度较高，在不同负载下具有较强的鲁棒性，可以在转速阶跃与斜坡变化时实现转子位置和转速的准确估算，拥有较高的动态与稳态性能。

3) 不足之处，此系统基于反电动势估计，适用于IPMSM中高速调速，所以，还需进行低速研究。