不等厚磁极永磁电机解析法分析
2018-08-09倪有源刘跃斌
倪有源,刘跃斌
(合肥工业大学,合肥 230009)
0 引 言
随着我国“十三五”规划的实施,高效、节能、经济、持续等成为能源发展新方向。永磁电机具有结构简单、体积小、功率密度高等优点,在舰船、航空、家电、医疗、公共生活等领域应用非常广泛[1,2]。
在永磁电机运行过程中,永磁体起着重要的作用。永磁体的求解一般有磁化矢量法和等效面电流法,两者出发点不同,但是得到的结果一样。而且任何磁场都可以看成是由分布电流产生的,在永磁体被完全磁化的情况下,磁极内部的等效面电流密度可以认为是零,永磁体的求解也就是转化为对磁极边的等效电流求解。
文献[3-5]分析了磁极内外弧圆心在同一点时,用等效面电流法求解径向和平行充磁条件下的气隙磁密分布。文献[3,4]在平行充磁条件下,对磁极外弧圆心发生偏移的永磁电机气隙磁密进行了等效面电流的分析求解,但是没有求解感应电动势和电磁转矩等参数。文献[6-9]运用磁化矢量法分析了磁极等厚的无刷永磁电机的开路场、电枢反应场以及负载场。文献[10]进一步提出并分析了等厚磁极磁场径向和平行磁化的改进模型。文献[11]在考虑槽的影响时,采用子域模型求解电机性能。文献[12]将磁极设置为等效的导体电流,然后将电机划分为2类子区域,进行气隙磁密和反电动势的解析求解。
对于永磁体内弧偏心的情形,本文通过等效面电流法求解不等厚磁极无槽永磁电机的气隙磁密,引入相对磁导函数,进一步求解有槽电机的气隙磁密、反电动势以及电磁转矩等参数。最后通过有限元法的计算结果验证了解析法的有效性,为电机在各种偏心情况下的参数计算提供了参考。
1 不等厚磁极永磁电机结构
从传统瓦形磁极内外弧圆心在同一点结构出发,得出磁极内弧圆心和外弧圆心发生偏移的一种磁极结构。在已知不等厚磁极最大厚度、最小厚度以及永磁矫顽力等参数的条件下,通过改善气隙磁密的分布来提高永磁电机的运行性能。传统瓦形内外弧圆心在同一点,即等厚磁极结构如图1所示。磁极内弧圆心偏移外弧圆心一定距离后,即不等厚磁极结构如图2所示。

图1 等厚磁极永磁电机结构

图2 不等厚磁极永磁电机结构
2 内弧偏心解析法求解
对于传统无槽等厚磁极结构的电机气隙磁密的求解,在文献[6]中给出了完整的解析式。对于内弧偏心磁极结构,分别在径向和平行2种磁化方式下,采用等效面电流法将磁极等效求解气隙磁密表达式。
2.1 径向充磁下的气隙磁密解析法求解
在图2的磁极内弧偏心结构中,R1为以O点为圆心的外弧半径,内弧偏心后磁极最小厚度为hmin,最大厚度为hmax。

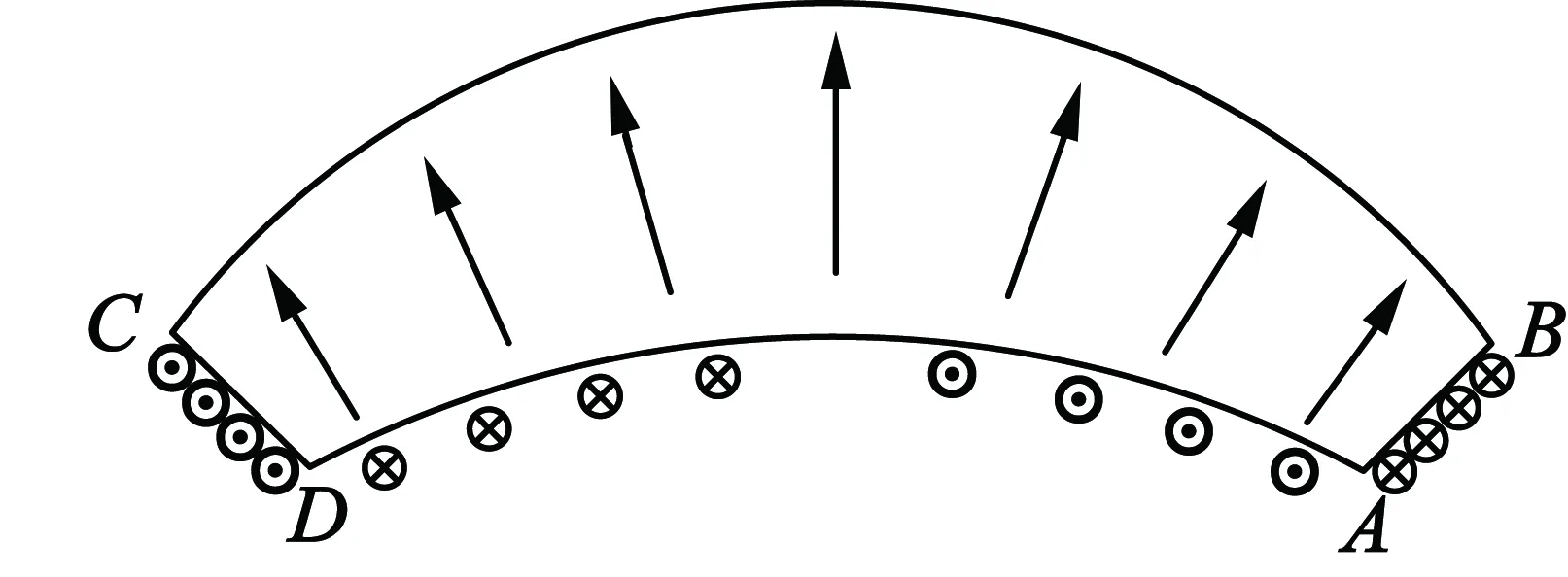
图3 径向充磁磁极等效面电流
由图2可见,OA=R1-hmin,O′A=R1-hmax+h,OO′=h。
在△OO′A中,根据余弦定理可得:
式中:αp为永磁体极弧系数;p为极对数。
永磁体的AD边和BC边的圆心距h:
在AD边,任意一点E到O点的距离:
AD边的等效面电流微元:
式中:
于是,该电流微元在气隙中产生的磁密:
式中:μ0为真空磁导率;Rs为定子内半径;θ为定子内表面上一点到磁极中心线的机械角度。
由以上各式通过积分,可得AD边的磁密:

(7)
式中:α是永磁体AB边到磁极中心线的机械角度。
而AB边和CD边的等效面电流微元:
di=Hcdr
(8)
根据等效面电流微元,可以求解在气隙中所产生的磁密:
对式(9)积分得到在定子内表面的磁密:

式中:
然后将AD边、AB边和CD边的气隙磁密叠加,得到每极的等效面电流法气隙磁密解析式。在一个周期内,对每极求解的结果进行叠加,就可以得到气隙磁密的分布。
2.2 平行充磁下的气隙磁密解析法求解
在已知条件不变的情况下,采用平行充磁时,如图4所示的磁极等效面电流可知,AB边和CD边的等效面电流方向相反,大小相同,而且面电流密度大小:
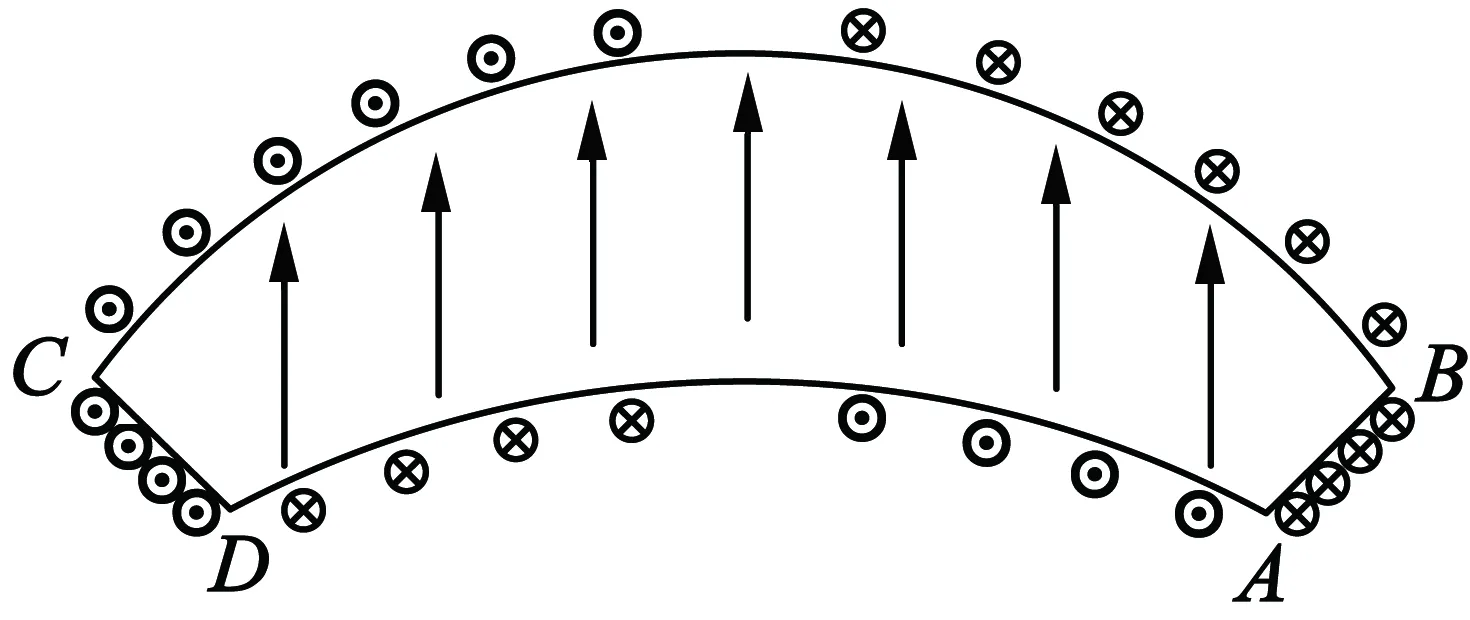
图4 平行充磁磁极等效面电流
BC边的等效面电流密度大小:
J2=Hcsinθ0(13)
AD边的等效面电流密度大小:
AB边和CD边的面电流产生的气隙磁密:
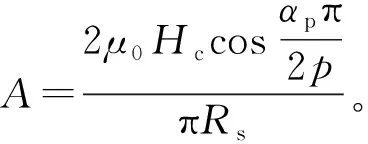
BC边的等效面电流微元:
di=Hc·sinθ0·R1·dθ0(16)
该电流微元在气隙中产生的磁密:
由以上关系式数值积分可以得到BC边磁密:

曲边AD的等效面电流微元:
其中:
那么该电流微元在气隙中产生的磁密:
由以上关系式积分,可以得到AD边的磁密:

式(15)和式(21)中:α和θ的含义与径向充磁的含义相同。
将AB边、CD边、BC边以及AD边求解的气隙磁密叠加,就可以得到平行充磁下的一个磁极气隙磁密解析式。
2.3 有槽结构电机的解析法分析
当求解有槽结构的电机性能时,由于有槽结构的子域解析求解比较复杂。因此在误差允许的条件下,通过引入相对磁导函数求解该电机的气隙磁密,并进一步获得感应电动势以及电磁转矩等参数的解析式。
对于有槽结构的永磁电机,相对磁导函数由文献[8]得出:
式中:b0为槽宽;α0=b0/Rs为槽宽对应的角度;αt=2π/Qs为槽距角;Qs为定子槽数;g′=g+hm/μr为有效气隙长度;hm为相对偏移角度对应的磁极厚度。当永磁电机为内转子结构时,即y=r-Rs+g′时,ν可以通过式(25)进行求解。

由式(23)~式(25)可以得到相对磁导函数的表达式:
将式(26)写成傅里叶形式:
有槽结构永磁电机气隙磁密的2个分量如下:
对于有槽结构的永磁电机,采用解析法求解反电动势时,空载径向气隙磁密:
式中:θma为取决于转速的相对位置角,表达式:
θma=ωrt+θ1(30)
式中:ωr为转子的机械角速度;θ1为转子的初始位置角。
由单个线圈的磁通,可获得各相绕组的感应电动势:
式中:N为每相总串联匝数;L为定子铁心长度;αc为线圈的节距角;Kdn=sin(npαc/2)为绕组的节距因数;Kqn为绕组的分布因数。
电机电磁转矩为感应电动势和电流的乘积,即:
式中:ei和ii(i=a,b,c)分别为定子三相绕组的感应电动势和电流。
对于定子电流,各相基波表达式分别如下:
式中:Im为每相电流的最大值;φ为相位角。
3 内弧偏心磁极电机性能分析
采用等效面电流解析法求解永磁电机气隙磁密,具有用时短、参数易优化等优点。本文对一台3相4极、采用径向充磁的永磁电机进行分析。电机额定转速为3 000 r/min。表1列出了该电机的主要参数。

表1 永磁电机参数
根据表1中的参数,首先通过文献[6]中的解析表达式,得到无槽等厚磁极永磁电机的气隙磁密分布。磁极厚度设置为5 mm。图5是径向充磁下的内外弧圆心在同一点的径向气隙磁密波形,图6是切向气隙磁密波形,与有限元法的结果完全吻合。

图5 无槽等厚磁极电机径向气隙磁密波形

图6 无槽等厚磁极电机切向气隙磁密波形
接着分析磁极内弧圆心偏移情况下的气隙磁密。在最大磁极厚度和最小磁极厚度为定值的情况下,改变最大磁极和最小磁极的数值,然后求解得到不同的偏心距离,再通过等效面电流法得到不同的偏心距下的气隙磁密、电磁转矩等参数。表2列出的是在径向充磁下,最大磁极厚度和最小磁极厚度发生变化时,2种方法计算得出的电磁转矩平均值。
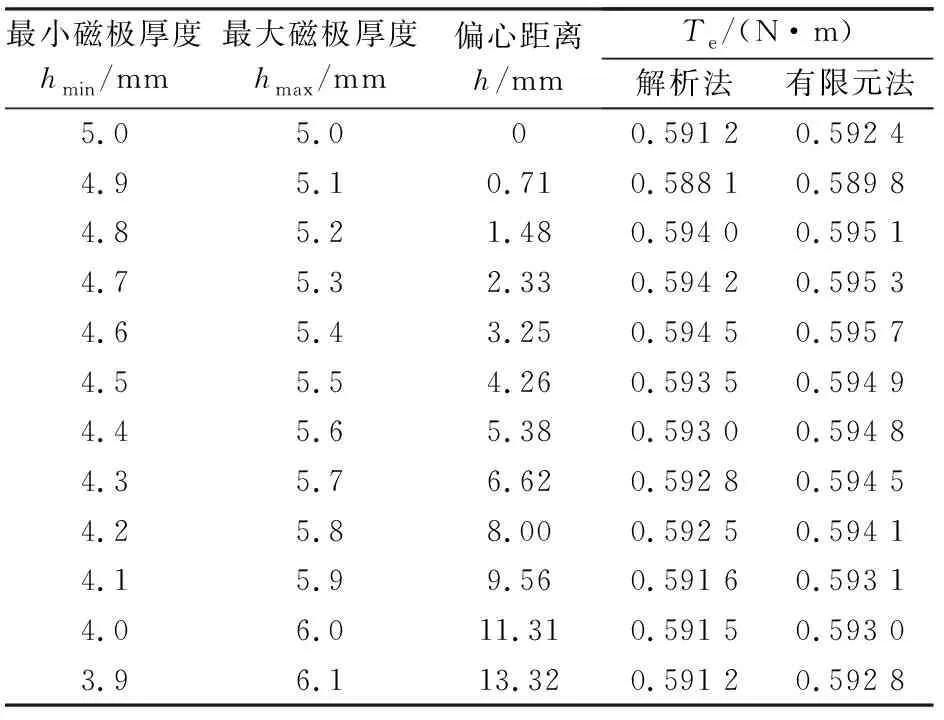
表2 不等厚偏心磁极的电磁转矩平均值
根据表2中的数据,选择最后一组数据,求解该电机在不同偏心距下的各种性能参数。径向充磁下,最大磁极厚度6.1 mm,最小磁极厚度3.9 mm。磁力线的分布可以精确反映电机内部的磁场强弱。在有限元计算中,获得的电机磁力线分布如图7所示。

图7 径向充磁电机磁力线分布图
对于有槽结构的电机,通过相对磁导函数求解气隙磁密。由式(23)~式(27)得到在定子内径处的相对磁导函数波形,如图8所示。
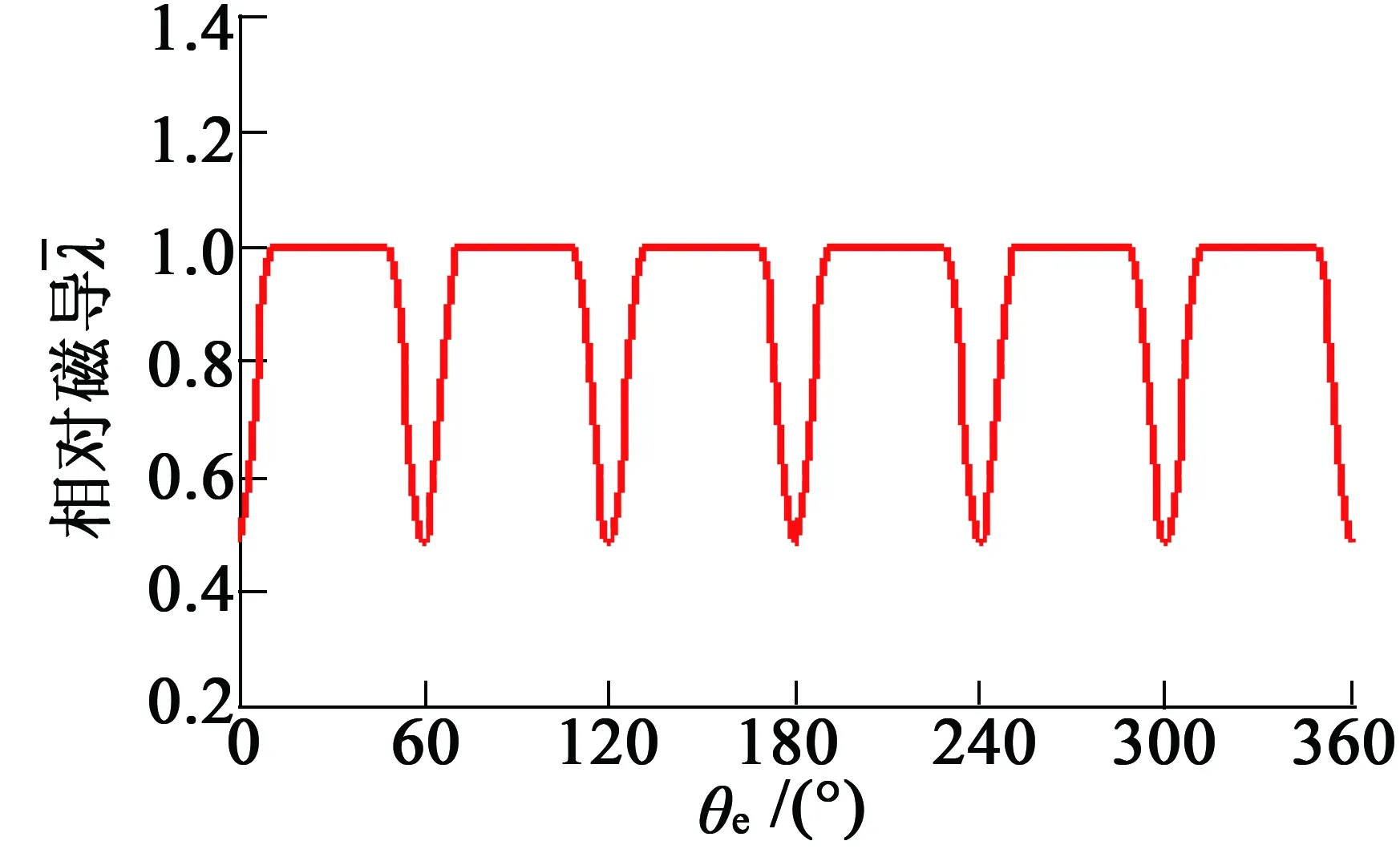
图8 定子内径处相对磁导波形
得到相对磁导函数后,由式(28)可以求出不等厚磁极有槽电机的径向气隙磁密,波形如图9所示。
然后对气隙磁密波形进行FFT谐波分析,可以得出径向气隙磁密的基波和谐波,如图10所示,其中基波幅值为0.686 T。
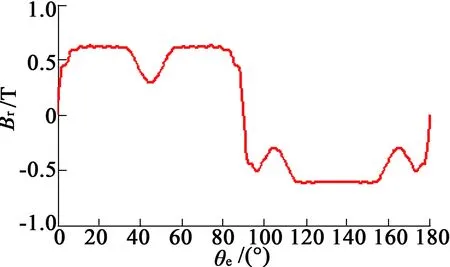
图9 电机径向气隙磁密波形

图10 电机径向气隙磁密FFT谐波分析
反电动势是电机性能分析的重要参数之一,反电动势与转子角速度、永磁产生的磁场、绕组匝数以及绕组分布有关。解析法和有限元法计算获得的a相感应电动势的波形如图11所示。由于实际槽深以及假设条件等多因素的影响,2种方法得到的波形存在误差,但整体一致性较好。

图11 电机的相感应电动势波形
电磁转矩也是电机的重要参数之一。电磁转矩不仅反映了电机的输出能力,而且电磁转矩脉动可以用来分析电机的振动和噪声,对电机的性能分析起着至关重要的作用。由式(32)获得的电磁转矩波形如图12所示。

图12 电机的电磁转矩波形
解析法获得的平均电磁转矩为0.591 2 N·m,有限元法获得的平均电磁转矩为0.592 8 N·m。二者的误差较小,从而验证了磁极等效面电流解析法的正确性。
4 结 语
本文采用磁极等效面电流的解析法,计算了内弧圆心偏移下的永磁电机电磁性能。通过此方法求解无槽结构永磁电机在不同磁化方式下的气隙磁密,通过引入相对磁导函数求解有槽电机的气隙磁密,进一步求解有槽结构电机的反电动势以及电磁转矩等参数。最后通过有限元法验证了解析法的正确性。结果表明,通过改变永磁磁极最大厚度和最小厚度,可以影响气隙磁密和电磁转矩等参数。本文的方法对电机各种偏心情况下的参数计算和优化设计提供了理论依据。
