基于Hartley变换的地磁场延拓技术

武立华,刘志海，孟 霆，黄 玉

(哈尔滨工程大学 理学院,黑龙江 哈尔滨 150001)

1 磁异常数据的Hartley变换

Hartley变换是一种类似于傅里叶变换的实数域积分变换方法， Hartley变换在图像处理、模式识别等许多领域内已被广泛利用[1-5]，但很少用于位场延拓处理中. 本文将Hartley变换应用到磁异常延拓积分迭代法中来提高运算效率.

设磁场场源位于平面z=0之下，z轴正向竖直向下，z<0空间中的磁异常分布f(x,y,z)是调和函数，z=0平面上的磁异常分布为已知观测数据，求解z<0空间中的磁异常分布函数f(x,y,z). 根据狄利克雷边值问题进行求解，得到磁异常延拓积分表达式为

(1)

令

将(1)式转化为卷积形式：

f(x,y,z)=f(ξ,η,0)*φ(ξ,η).

(2)

由文献[6]可得φ(ξ,η)的Hartley变换结果为

(3)

根据Hartley变换的卷积性质可以得到对应的Hartley变换形式：

H(u,v,z)=H(u,v,0)·φH(u,v),

(4)

式中，H(u,v,z)表示所求解f(x,y,z)的Hartley变换形式，H(u,v,0)表示已知磁异常分布数据f(x,y,0)的Hartley变换形式. 对(4)式进行Hartley逆变换可以得到所求平面的磁异常分布：

φH(u,v)cas (ux)cas (vy)dudv.

(5)

2 模型数据仿真

使用球形磁体模型计算得到z=195 m平面上的磁异常理论值,如图1所示.

分别通过传统的波数域迭代法和Hartley变换迭代法将z=0平面上的磁异常数据向下延拓至z=195 m平面. 图2即为2种方法所得到的延拓结果的磁异常分布等值线图.

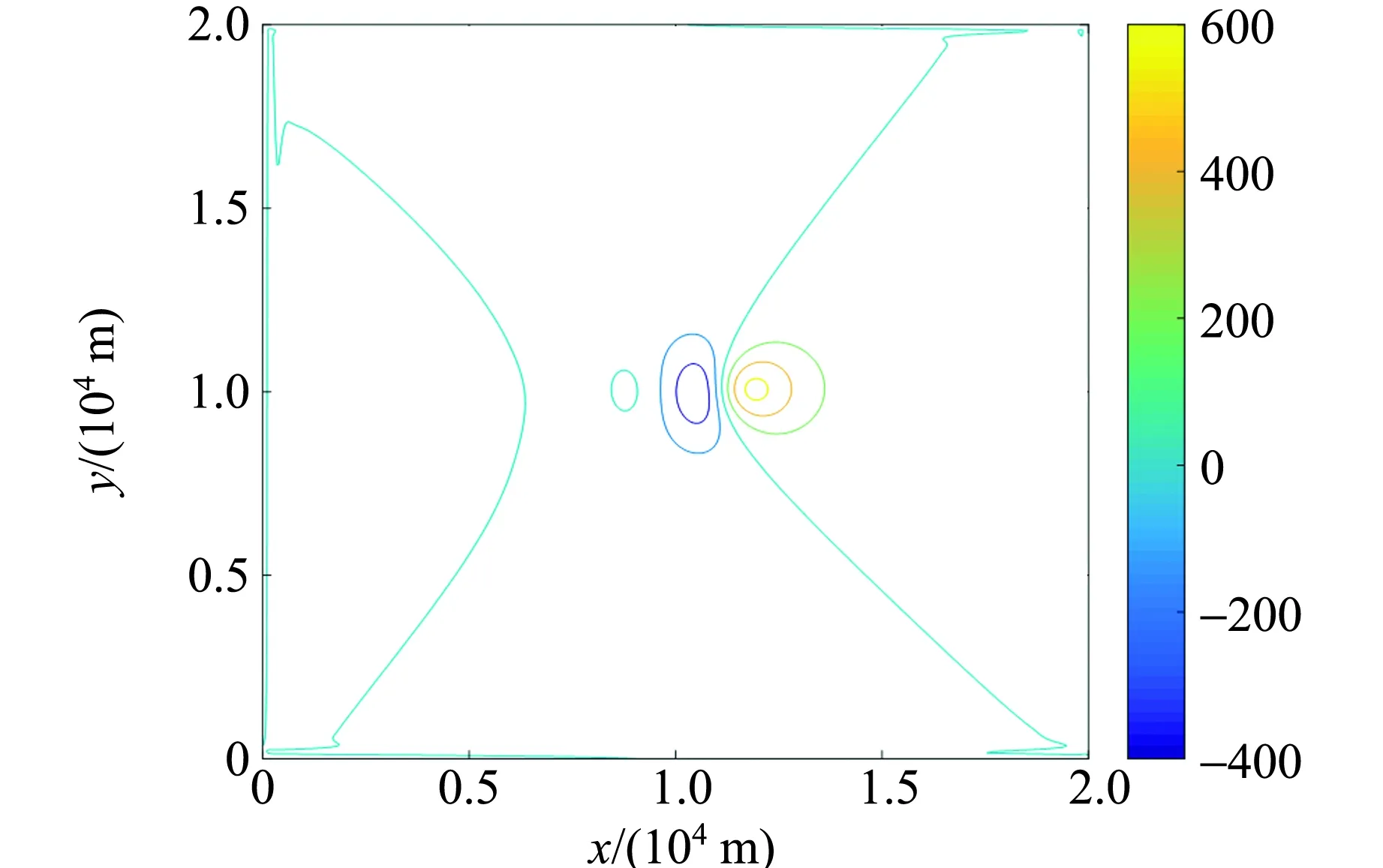
(a)利用Hartley变换的迭代法

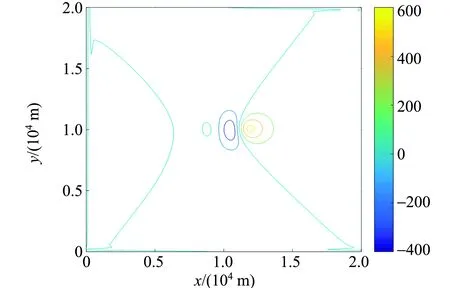
(b)传统快速傅里叶变换迭代法图2 利用2种迭代法向下延拓195 m后的磁异常分布

从图2可以看出，经过2种迭代法处理后所得数据分布几乎完全相同，这是由于在数据处理方面，Hartley变换和傅里叶变换的作用是一致的. 为了体现这种相似性，也为了更好地描述向下延拓的稳定性，在此引入3种误差指标：绝对平均误差、平均相对误差和均方根误差. 对图2中的2种延拓结果分别进行误差计算，2种迭代法的误差相同：绝对平均误差为0.31 nT，平均相对误差为0.45%，均方根误差为2.5 nT，但Hartley变换迭代法用时2.035 4 s，傅里叶变换法用时3.254 6 s，因此Hartley变换迭代法效率更高.

3 实验检验

文中所用真实数据下载自美国国家地球物理数据中心(NGDC)，其原始数据为一定范围平面内的磁异常数据. 设其原始平面为z=0平面，其磁异常数据等值线图如图3所示. 设定网格间距为100 m，计算网格为512×512. 为了进行向下延拓算法测试，首先利用向上延拓算法将原始数据平面向上延拓1 000 m，得到z=-1 000 m平面的磁异常分布数据如图4所示.

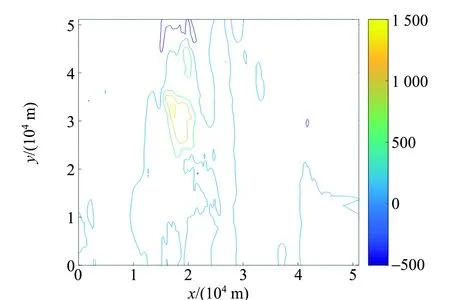
图3 z=0观测平面理论磁异常分布

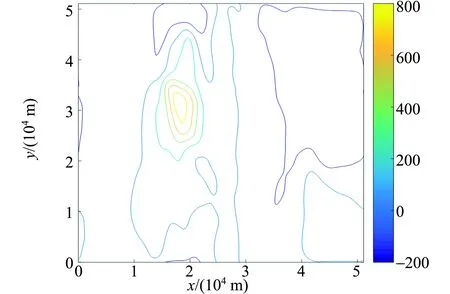
图4 向上延拓得到的z=-1 000 m平面磁异常分布

接下来进行s=1，n=100的迭代运算，分别使用Hartley变换迭代法和传统迭代法将z=-1 000 m平面的磁异常数据向下延拓1 000 m，得到如图5所示的z=0平面上的延拓数据，将其和观测平面理论数据(即原始平面数据)进行对比并计算误差，同时对运算时间进行统计，2种迭代法的误差相同：绝对平均误差为7.2 nT，平均相对误差为0.25%，均方根误差为17.1 nT，Hartley变换迭代法用时4.286 3 s，傅里叶变换法用时10.255 6 s.

由图5可知，通过2种方法进行向下延拓后的结果与原始数据基本一致. 此外3种误差的值都很小，在实际需求可接受的范围内，但相比理论实验误差有所增大，这是由于真实数据中存在噪声而产生的，但2种方法对噪声还是有一定的抗干扰能力的. 对比2种方法的运算时间可以发现，基于Hartley变换的迭代法效率要高出很多，因此优于传统迭代法.

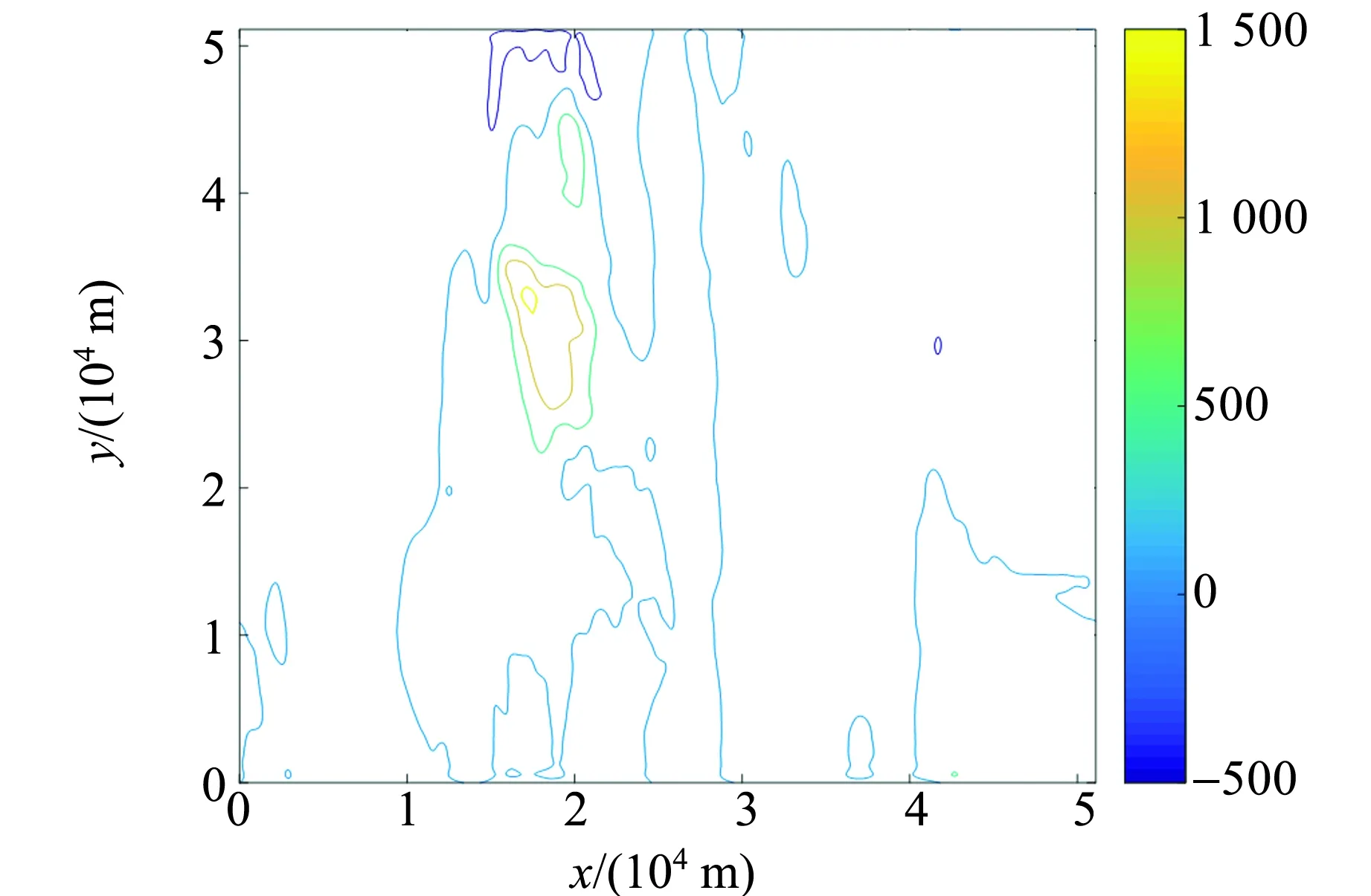
(a)Hartley变换迭代法延拓结果

(b)传统迭代法延拓结果图5 利用2种迭代法向下延拓1 000 m后得到的磁异常分布

4 结束语

通过理论模型和真实数据的仿真测试对Hartley变换算法进行检验，并利用绝对平均误差、平均相对误差和均方根误差3种误差统计指标对算法的误差进行了统计，从而对Hartley变换的迭代法和传统快速傅里叶变换迭代法进行了比较，证明利用Hartley变换的磁异常向下延拓迭代法的可行性和高效性.